空调室外机管路系统的模态仿真分析

张宁波,汪建晓,张立平

(佛山科学技术学院，广东佛山 528000)

空调室外机管路系统的模态仿真分析

张宁波,汪建晓,张立平

(佛山科学技术学院，广东佛山 528000)

空调管路中的排气管和回气管在长期工作下因振动而产生疲劳和松动，这将会影响管路的使用性能。针对空调管路振动问题，建立了管路模型，运用ANSYS中的workbench模块对管路进行模态分析和谐响应分析，并对比分析了阻尼和管路结构对系统固有频率的影响，通过改变固有频率来避开管路共振。

管路振动；模态分析；谐响应分析；workbench

1 前言

空调室外机在工作过程中总会产生振动和噪声，这些振动和噪声给人们的生活造成了一定的影响。长期的振动会导致空调各零部件松动且使用性能下降。空调室外机的振动主要来源于压缩机，压缩机在工作过程中不仅会产生强烈的振动，同时压缩机产生的振动会传递到与之相连的管路上。管路是空调冷媒运输的重要部件，长期的振动会使得管路产生疲劳和松动，甚至导致冷媒的泄漏。根据调查可知，管路振动是空调故障中的首要破坏因素之一[1]。因此需要对管路进行着重研究，降低管路振动大小，提高管道使用性能。文献[2-4]对空调管路进行了简单的模态分析，提出了合理的管路设计方法。文献[5]研究了管路壁厚和阻尼配重对管路振动模态的影响，提出了管路结构设计的合理建议。文献[6]对管路进行了有限元分析，并在管路不同部位施加约束位移，通过对比分析得出了管路最佳优化结果。文献[7]简述了有限元分析技术在空调应力应变分析中的重要性。本文在上述研究的基础上，着重对空调室外机管路进行模态分析和谐响应分析，并对比分析2种减振措施的效果。

2 管路模态分析

2.1 模态分析基本理论

对管路进行模态分析，可以得到管路的各阶固有频率大小和各阶固有频率下相应的振型[8]。管路是一个连续振动系统，其模态分析即为分析管路在没有外界激励和略去阻尼作用下其各阶固有频率和相应振型，其计算公式为：

(1)

式中 [M]——质量矩阵 [K]——刚度矩阵

无阻尼模态分析求解的基本方程为求解特征值问题，即：

(2)

式中 {φ}i——特征向量，表示第i阶振型ωi——第i阶固有频率

2.2 压缩机激励频率计算

压缩机间歇性吸气和排气产生的振动作为激振力传递给管道，导致管道产生振动。当压缩机的激励频率和管道固有频率接近时会导致共振，因此需要计算出压缩机的激励频率来避开共振点。压缩机激发频率计算公式为[9,10]：

fy=mn/60

(3)

式中fy——压缩机激励频率m——曲轴每转一周向管道吸气或排气的次数，单作用压缩机m=1，双作用压缩机m=2

n——压缩机曲轴转速

通过数据收集可知，空调压缩机的转速n为2850～2980r/min。根据某型空调，其单作用压缩机转速为2900r/min，借助式(3)可算出压缩机激励频率为48.3Hz。为了避免激励频率与管路结构固有频率接近而导致结构共振，需对管路系统进行模态分析。

2.3 管路模态分析

在实际应用中，空调管路材料一般为紫铜，其弹性模量为1.27×105MPa，密度为8900kg/m3，泊松比为0.33。四通阀材料为黄铜，其密度为8900kg/m3,弹性模量为1.23×105MPa，泊松比为0.34。四通阀总质量为300g，模态分析中，对四通阀构件进行等效质量处理。根据某型1P空调，对四通阀模型进行简化处理后，其管路模型如图1所示。

图1 管路模型

在图1中，排气管端口与压缩机相连接，回气管端口与液体收集器相连接，四通阀对空调制冷制热功能进行控制。借助ANSYSWorkbench软件对管路进行模态分析，由于冷凝器和低压阀接管与固定端相连接，因此在这两处施加固定约束[11]。相对排气管和回气管而言，压缩机刚度很大，因此在回气管和排气管与压缩机相连的端口施加固定约束。对管路进行模态分析时，提取管路前10阶固有频率，如表1所，并提取了管路的第1阶和第2阶振型图，如图2(a)和(b)所示。

表1 管路前10阶固有频率

(a) 第1阶振型

(b) 第2阶振型

从表1可知，管路的第1阶固有频率为48.729Hz，与压缩机激励频率48.3Hz极为接近，容易产生共振现象。同时，由图2管路振型图可看出，管路振动主要表现在回气管下端U型部位和排气管下端L型部位，其振动方向主要为前后摆动，即X和V方向。针对此现象，本文对影响管路模态的相关因素进行了仿真分析。

3 模态影响因素仿真分析

3.1 阻尼对管系固有频率影响

对管路进行模态分析分析时可知，在回气管下端U型部位和排气管下端L型部位产生的振动变形较大，因此考虑分别在此两处部位施加阻尼块，主要是将阻尼块包裹在管路上。阻尼块材料为橡胶，弹性模量为10MPa，密度为860kg/m3，泊松比一般在0.45～0.50之间。空调回气管和排气管施加阻尼块模型如图3(a)和(b)所示。

(a) 回气管施加阻尼块模型

(b) 排气管施加阻尼块模型

对分别施加阻尼块的管路进行模态分析，在管路4个端口分别施加固定约束，并提取管路前10阶固有频率和第1阶振型图，分别如表2和图4(a)和(b)所示。由表2可知，回气管施加阻尼块后，管路第1阶固有频率变为46.969Hz，有效地避开了压缩机激励频率48.3Hz。而排气管施加阻尼块后，管路的第1阶固有频率为48.182Hz，与压缩机激励频率48.3Hz极为接近，不能有效的避开激励频率。

表2 管路施加阻尼块的前10阶固有频率

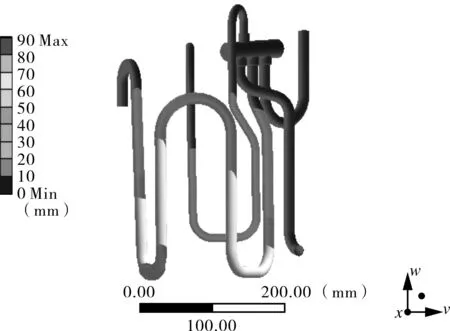
(a) 回气管施加阻尼

(b) 排气管施加阻尼

由图4可知，在管路排气管和回气管分别施加阻尼后，管路第1阶振型最大变形处为排气管下端U型管处，其主要运动方向回气管和排气管的前后摆动。通过对比分析可知，在回气管上施加阻尼块，可以有效地影响管路固有频率，达到避振的目的。

3.2 优化管路结构对管系固有频率的影响

排气管与压缩机相连，长期受到来自压缩机工作时振动的影响，同时压缩机和排气管产生的振动会传递到回气管上。在管路结构优化设计中，排气管尽量采用L型管，回气管尽量采用U型管。管路优化模型如图5所示。

图5 优化管路模型

对优化管路模型进行模态分析，提取管路前10阶固有频率和第1阶振图，分别如表3和图6所示。

表3 优化管路结构前10阶固有频率

图6 新模型第1阶振型图

通过表3可看出，对管路结构进行优化后，管路第1阶固有频率提高到56.992Hz，有效的避开了压缩机激励频率48.3Hz。由图6可看出，新模型第1阶振型变形最大值为排气管下端L型部位，其运动方向主要表现为回气管和排气管的前后摆动。即合理设计管路结构可以有效地改变管路固有频率，从而达到避振的效果。

4 管路谐响应分析

谐响应分析是用来确定结构承受简谐变化载荷时的稳态响应，计算结构在稳态受迫下的振动大小。压缩机在工作过程中间歇性的吸气和排气所产生的激振力属于简谐变化载荷。管路长期受到压缩机所产生的简谐激振力而产生相应振动，因此还需对上述管路振动进行谐响应分析。外界激励一般在低频范围，因此管路振动频率分析范围为0～150Hz。对比了上述施加阻尼块的管路部位在原模型、回气管施加阻尼块和优化管系结构3种情况下最大位移值。如图7所示。

图7 管路变形位移值

由图7可知，对管路进行响应分析时，原模型、施加阻尼模型和新模型其最大位移值分别为0.84147，0.34112，0.35624mm。由此可知，施加阻尼块模型和新模型的位移值有明显的下降。

5 结语

通过本文对比分析可知，在对管路进行模态分析和谐响应分析时，仿真模拟可以有效地分辨出管路避振方法的合理性与可靠性。在空调管路的实际工作过程中，管路总会受到外界激励的影响，会产生更大的应力和变形，因此需要提高管路本身的固有特性，加强管路本身的结构设计，提高管路的抗振性能，避开激励频率，并通过施加一定的外部约束条件来达到减振避振的目的。

[1] 赵文龙，张增学，李立斌.有限元技术在空调器管路振动分析及设计优化中的应用[J].华南农业大学学报,2004(3):112-115.

[2] 张进.空调器管路振动分析及优化工作中有限元技术的应用[J].科技创新导报,2011(19):71.

[3] 邢立梅.简述基于仿真及测试的空调管路设计[J].黑龙江科技信息,2012(26):47.

[4] 麦志炜，苏运宇.基于CAE技术进行空调管路模态分析[J].科技创业家,2013(8):3-5.

[5] 张晓伟，李苏洋.空调管路系统的振动分析[J].振动测试与诊断，2012(S1):120-122.

[6] 张敬东，起雪梅，杜仕武.空调管路振动性能分析及优化设计[J].重庆邮电大学学报(自然科学版),2013(5):705-710.

[7] 陈思磊.有限元技术在空调管路振动分析中的应用思路构建[J].科技风,2014(5):91.

[8] 谭蔚，晋文娟，吴皓，等.刚性管对正方形排布管束流体弹性不稳定性的影响研究 [J].压力容器，2016,33(3):1-8.

[9] 袁伟，赵杰，李峰，等.压缩机管线振动机理及减振技术研究综述 [J].化工设备与管道，2016,53(2):36-42.

[10] 樊长博，张来斌，王朝晖，等.往复式压缩机气体管道振动分析及消振方法[J].科学技术与工程,2007(7):1309-1312.

[11] 杨靖.空调器配管的有限元分析[J].流体机械,2002,30(11):61-64.

The Air Conditioner Outdoor Unit Modal Simulation Analysis of Piping System

ZHANG Ning-bo,WANG Jian-xiao,ZHANG Li-ping

(Foshan University，Foshan 528000,China)

The exhaust pipe and return pipe will produce fatigue and loose under the long-term vibration.It will influence the use of performance of pipes.In order to study the vibration of pipeline.The pipeline model was established based on workbench software,and the modal analysis and harmonic response analysis were carried out.Compared the natural frequency of damping and pipeline structure,by changing the natural frequency to avoid resonance.

pipeline vibration;modal analysis;harmonic response analysis;workbench

1005-0329(2017)02-0071-04

2016-05-30

国家自然科学基金项目(51405083)；广东省高校优秀青年创新人才培养计划资助项目(2014KQNCX186)；佛山科学技术学院优秀青年教师培养计划项目(fsyq201409)

TH137；TG925.12

A

10.3969/j.issn.1005-0329.2017.02.016

张宁波(1991-)，女，在读研究生,主要从事机械工程方面的研究，E-mail:1172331158@qq.com。

张立平(1979)，女，博士，副教授，主要从事机械系统动力学及振动噪声控制的研究，通讯地址：528000 广东佛山市禅域区江湾一路18号佛山科学技术学院机电工程系，E-mail:lpzhangok@163.com。