考虑运输时间的柔性作业车间调度问题研究

杨立熙，余慧慧

(福州大学 经济与管理学院，福建 福州 350108)

考虑运输时间的柔性作业车间调度问题研究

杨立熙，余慧慧

(福州大学 经济与管理学院，福建 福州 350108)

在实际加工生产中，工序间的运输时间占整个加工时间的比例很大。为了更合理地研究柔性作业车间调度问题，将运输时间作为独立影响因子考虑到模型中。针对模型的特殊性与传统遗传算法易早熟的缺陷，运用小生境的思想和自适应距离变量划分种群并协同进化，进而平衡种群选择压力，避免算法过早收敛至局部最优。同时提出最短工作时间方法优化初始种群，改善算法的求解效率。运用Matlab对国际上通用的算例进行实验并与经典遗传算法对比，结果表明，新提出的算法能够获得更优的调度方案。

柔性作业车间调度；运输时间；遗传算法；小生境；选择压力

随着自动化技术的发展和柔性制造系统的出现，近年来柔性作业车间调度问题(flexible job-shop scheduling problem，FJSP)成为研究重点。FJSP已经被证明是NP-Hard问题，求解方法主要是群体智能优化算法，如遗传算法(genetic algorithm，GA)[1]、蚁群算法(ant colony algorithm，ACO)[2]、粒子群算法(particle swarm optimization，PSO)[3]等。但大多数关于FJSP的研究忽略了工序之间的运输时间，而运输时间却是实际生产中客观存在的，若放宽过多的假设条件会导致理论研究缺乏指导性，而且在一些特定的生产领域，其运输时间过长会直接影响产品的质量。

目前，考虑运输时间的FJSP的研究相对较少。HURINK等[4-5]假定物料处理系统间存在运输时间，以最小化完工时间为优化目标，运用禁忌搜索算法寻求局部最优解；李峥峰[6]利用传统遗传算法求解了考虑运输时间因素影响的柔性车间调度问题，测试结果表明考虑运输时间的柔性车间调度模型具有极强的优化性能，其平均改进结果达到33.6%；王永峰[7]在传统遗传算法的基础上，设计了一种机器选择的启发式算法作为初始解改进算法加以求解；ZHANG等[8]借助遗传算法和禁忌搜索算法解决了考虑运输时间的柔性调度问题；赵宁等[9]在研究考虑运输时间的柔性作业车间调度过程中，建立了两阶段求解方法。遗传算法是求解此类组合优化问题的有效方法，但上述文献未考虑到算法易早熟、容易陷入局部最优的弊端。笔者研究考虑运输时间的FJSP，提出一种小生境遗传算法。在遗传算法的框架下，结合小生境的思想划分种群进行局部寻优，平衡种群选择压力以克服GA易过早陷入局部最优的缺点。并针对优化目标提出新的初始化方法，以期改善考虑运输时间的FJSP的求解速度和求解质量。

1 问题描述

考虑运输时间的FJSP的描述如下：n个工件{J1,J2,…,Jn}要在m台机器{M1,M2,…,Mm}上加工。每个工件包含一道或者多道工序，工序的顺序是预先确定的，每道工序有一台或者多台加工机器可供选择，选择不同的加工机器对应的加工时间和运输时间也不同。调度需要为每道工序选择合适的加工机器、确定每台机器上各工序的最佳加工顺序和开工时间，使整个系统的性能指标达到最优。此外，在加工过程中不仅要考虑工序顺序和设备资源的约束，还要考虑工序间的运输时间约束，笔者作出如下假设:①每个工件的加工一旦开始不能中断，即加工过程为非抢占式；②同一台机器同一时刻只能加工一个工件；③设备在零时刻可用，所有工件的第一道工序在零时刻都可以被加工；④所有工序按先后顺序加工，每一道工序加工完毕后立即运输到下一加工工序的设备，下一道工序方可加工； ⑤工序加工时间因所选的加工设备不同而不同，加工时间是给定的；⑥同一工件的相邻工序之间存在加工运输时间，运输时间因相邻两道工序选择的加工机器的不同而不同，且机器间的运输时间是给定的。

数学模型描述及定义为： 工件集J={J1,J2,…,Jk,…,Jn}，Jk为第k个工件(k=1,2,…,n)；机器集M={M1,M2,…,Mi,…,Mm}，Mi为第i台机器(i=1,2,…,m)；Ojh为第j个工件的第h道工序，并定义Oj(h-1)表示第Ojh的前一道工序，Oj′h′表示Ojh当前所在机器的前一道工序；Pijh为第j个工件的第h道工序在机器i上加工所需时间；Sijh为第j个工件的第h道工序在机器i上的开始加工时间；Cijh为第j个工件的第h道工序在机器i上的结束加工时间；Transtimeie为机器Mi和机器Me之间的运输时间；Cj为第j个工件的完工时间；Cmax为最大完工时间。考虑最小化最大完工时间(makespan)，目标函数及其约束条件分别为：

(1)

Cijh=Sijh+Pijh

(2)

Cijh-Cij′h′≥Pijh

(3)

Sijh=

(4)

式(2)表示工序的完工时间等于开始时间与加工时间之和，即加工为非抢占式；式(3)表示机器资源约束，即假设2；式(4)表示若工序所在机器的可开始加工时间小于前一道工序运输结束时间，则受运输时间约束；否则，工序受当前加工机器的资源约束。因此，对于同一机器的相邻工序而言，仅受机器资源约束；对于同一工件内的相邻工序而言，考虑了运输时间，替代了传统模型中的工序顺序约束。

2 改进遗传算法

2.1染色体编码和解码

编码和解码是遗传算法首要解决的问题，用于将问题解和染色体相互转换。FJSP包括工序排序和机器选择两个子问题，将两个子问题融合成一条染色体，即表示为柔性作业车间调度的一个可行解。 ①工序排序部分：采用基于工序的实数编码。基因串长度为总工序数，每个基因位置用工件号表示，其中每个工件号出现的次数代表该工件的工序数。如一个可行基因串1-1-2-2-1，对应的工序顺序是O11-O12-O21-O22-O13。 ②机器选择部分：采用基于机器分配的编码。基因串长度为总工序数，从左到右依次按工件工序顺序排列，基因位置代表工序对应加工机器。例如一个可行基因串1-3-1-1-2，表示工序O11在可选机器的第1台机器M1加工，工序O12在可选机器的第3台机器M4加工，依次类推。具体编码如图1所示。

图1 染色体编码

解码时需要考虑两个问题：①工序顺序和机器资源约束，插入式主动调度如图2所示，以工序O13为例，其前一道工序O12的运输完成时间大于当前机器可加工时间，此时受机器资源约束；②文献[10]已证明正规性指标的最优调度存在于主动调度集中，因此在图1的初始解码的基础上，判断当前机器是否存在空闲时间。若存在空闲时间且大于该工序的加工时间，则将当前工序插入到间隔时间段中，确保生成主动调度集，以图2工序O21为例。

图2 插入式主动调度

2.2初始化方法

初始解的优劣影响算法的求解质量和收敛速度。目前使用较多的是随机初始化，这种方法操作简单，但是初始解参差不一，需要增加迭代次数或者种群规模来寻求较优解。由于模型中考虑了运输时间，使得可行解的搜索范围扩大进而问题求解更为困难。故笔者提出考虑工序加工时间和运输时间因子影响的最短工作时间法(short working machine,SWM)，赋予各个工序选择近似较优的机器来获得较优的初始解，缩短算法收敛寻优的收敛时间。同时为保持初始种群多样性，初始化采用一半SWM，一半随机初始化方法生成。

SWM执行步骤为： ①获取工件集总数J_O_number，每个工件Ji对应的工序数size(J(i)，O)；②设置一个整型数组Idx，用于记录机器索引号；设置一个整型数组chrom_M，长度等于总工序数，用于记录SMW算法的机器选择部分，初始化数组元素值为0；③随机选择一个工件，并选择当前工件的第一道加工工序；④寻找当前工序的可选择加工机器及加工时间，选择时间最小的那台机器作为当前工序的加工机器，更新Idx和chrom_M，并以此作为下一次选择依据；⑤选择当前工件的下一道工序，并记录工序的可选机器及对应加工时间，从Idx中获取上一道工序加工机器索引号，计算相邻工序间的运输时间，不更新数组；⑥将加工时间与运输时间相加，选择相加和最小的那台机器作为当前加工机器，更新Idx和chrom_M；⑦重复步骤⑤和步骤⑥，直至当前工件所有工序的加工机器选择完毕；⑧从工件集中选择下一个工件，同时选择工件的第一道工序，重复步骤④～步骤⑦，直至工件集中所有工件被选择完毕。chrom_M即表示最短工作时间法产生的机器选择初始化，以J1为例，SWM计算逻辑如图3所示。

图3 SWM计算逻辑

2.3交叉算子

交叉的目的是通过父代个体的信息交换，保留父代中优良信息，产生新的子代。染色体有两部分组成，分别采取不同的操作方式。①工序染色体：该部分是基于工序编码，传统的随机选择交叉简单易操作，但是容易产生不可行解，因此该部分采用文献[11]提出的POX交叉法，继承父代染色体工序排序部分的优良基因。首先，将工件集J随机划分成两个非空子集Job1，Job2；其次，将父代染色体P1/P2中包含Job1/Job2的工件复制到子代C1/C2中，并保持其位置和顺序不变；最后，将父代染色体P1/P2中包含Job2/Job1的工件复制到子代C2/C1中，并保持其顺序不变。②机器染色体：为保证此部分交叉后产生的仍是可行解，采用多点交叉(MPX)方式，即随机选取多个交叉点，两父代进行基因块交换。

2.4变异算子

变异是通过随机改变染色体的某些基因，产生新的染色体，从而增加种群的多样性，改善GA的局部搜索能力。①对于工序排序部分，采用互换操作，即随机选择两个不同位置的基因进行交换。②对于机器选择部分，随机选择一个基因位，在该位置的可选机器上随机选择一个加工机器代替当前染色体中的加工机器。

2.5小生境进化策略

选择压力过大是导致GA早熟收敛至局部极值的一个重要原因。随着进化的进行，优秀个体的重抽样机会增多，使得靠近局部最优解而非全局最优解的个体更容易被选择，导致种群过早陷入局部最优。因此，笔者借鉴小生境的概念，通过设定一个自适应距离隔离小生境，将种群划分成两个子种群，分别按适应度值排序保留较优解于精英库，结合遗传算法的交叉变异规则更新，最后合并得到新一代种群，进化策略如图4所示。

从概率上讲，与最优解有较大相似度的个体也有较高的适应度[12]，小生境隔离策略以当前最优点为中心，将种群划分成两部分。小于阈值d表明与最优解有较高的相似度，划分到优质子种群pop1；其余个体划分到次优子种群pop2。其中子种群pop1为提高整体适应度；子种群pop2为保持种群多样性。由于遗传算法是按照染色体编码的方式计算，因此在种群划分中引入海明距离的概念:

图4 小生境进化策略

⊕Op2(i)+

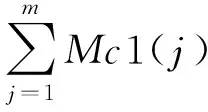
式中:C1和C2表示两条染色体；Op1和Op2表示C1和C2工序排序的编码部分；Op1(i)、Op2(i)表示第i位基因；Mc1和Mc2表示C1和C2机器分配编码部分；Mc1(j)、Mc2(j)表示第j位基因；n和m分别表示工序排序部分和机器分配部分的染色体长度。⊕为异或运算符，其定义为：

A⊕

按照海明距离定义小生境，以期在子种群pop1中寻求一个局部最优值即为当前全部最优。初期无法界定两个局部最优值的距离，故采用固定阈值d是不准确的。笔者采用自适应的阈值，即随着进化的进行，d会逐渐缩小，直至剩余个体都集中于一个局部极小值附近。阈值d和种群划分规则定义如下：

其中，dk=0.5min (max (x,xm))，表示每k代随种群变化的划分阈值。随着迭代次数的增加，当d足够小时，表明种群个体趋于近优解，定义pop2为空集，即个体全部集中于优质子种群pop1。

2.6改进GA的执行步骤

单一的遗传算法存在局部搜索能力差的缺陷，笔者综合考虑带运输时间的FJSP，利用遗传算法实现全局搜索，小生境划分实现局部搜索，两者结合发挥各自的算法优势。改进遗传算法具体

执行步骤为：①确定种群规模、迭代次数Gen、交叉概率Pc、变异概率Pm等参数；②种群初始化。采用一半SWM，一半随机初始化法；③利用小生境进化策略将种群划分成两个子种群pop1，pop2；④分别评价种群中每个染色体适应值，并按大小排序，如果满足条件输出近优解；否则执行步骤⑤；⑤精英库中的个体直接保留至下一代，其余执行锦标赛选择策略；⑥对满足交叉概率的染色体个体按照交叉策略进行交叉；⑦对交叉后得到的种群满足变异概率的染色体按照变异策略进行变异，得到新一代种群；⑧按照精英策略对精英库进行更新；⑨合并子种群pop1，pop2；⑩返回步骤③。

3 计算结果与比较

为验证该改进遗传算法的有效性，采用Matlab编写运行代码，程序在处理器为P4 CPU，主频为2.13 GHz，内存2 GB的个人计算机上运行。设置种群规模为100，最大迭代次数Gen=200，Pc=0.8，变异概率Pm=0.1，一半最短工作时间法初始化，一半随机初始化。对每组算例运行10次，取其最优解。从两方面展开对比实验：①与传统GA对比算法的质量效率；②与不考虑运输时间的最优调度方案对比最优结果。

测试算例选择国际上通用KACEM等[13-14]提出的3个标准算例进行测试，包含8×8的P-FJSP、10×10的T-FJSP和15×10的T-FJSP，这些数据是FJSP问题中普遍采用的。考虑到现实问题中存在不同程度的设备运输情况，将运输时间按照平均加工时间、最大加工时间分成0～1，1～5，5～10 这3个等级(KACEM算例中最长加工时长为10)，参考文献[9]采用的随机函数法生成。1～5之间分布和相关实验结果对比分别如表1和表2所示。

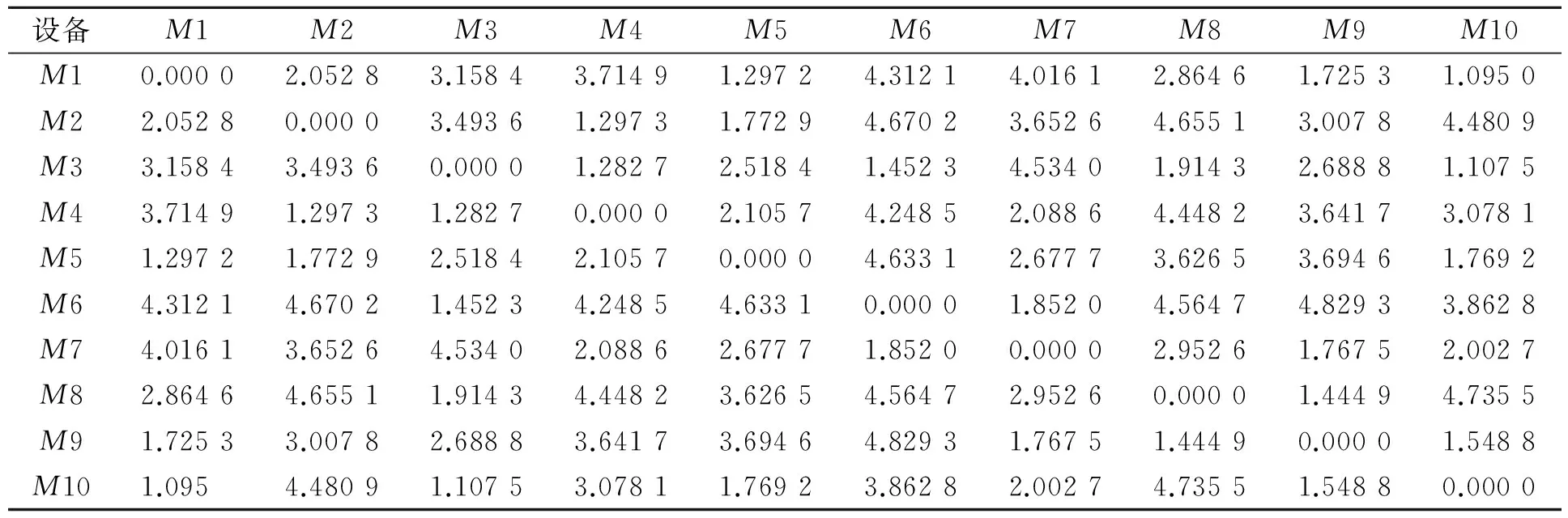
表1 在1～5之间分布的设备间运输时间

表2 实验验证结果对比

其中，Cmax表示当前算法的最优解；RE1表示此算法与传统GA间的相对误差；RE2表示此算法与KACEM最优调度中加入运输时间求解的相对误差。计算结果表明，不论是与传统GA还是与加入运输时间的最优调度方案相比，笔者提出的改进算法总能得到更好的近优解。并且随着工件数量和机器选择的增加，RE越来越大，这说明对于大规模工件和柔性车间，笔者算法的优势更明显。从相对误差来看，基本上RE2大于RE1，说明考虑运输时间的调度更符合实际优化。

以算例8×8(运输时间在1～5)为例，改进算法和原始GA的调度甘特图对比如图5所示，圈出的部分即表示工序J62的加工及相应的运输部分。运用改进算法得到最优调度如图5(a)所示，makespan为21.462 7；对应传统遗传算法对

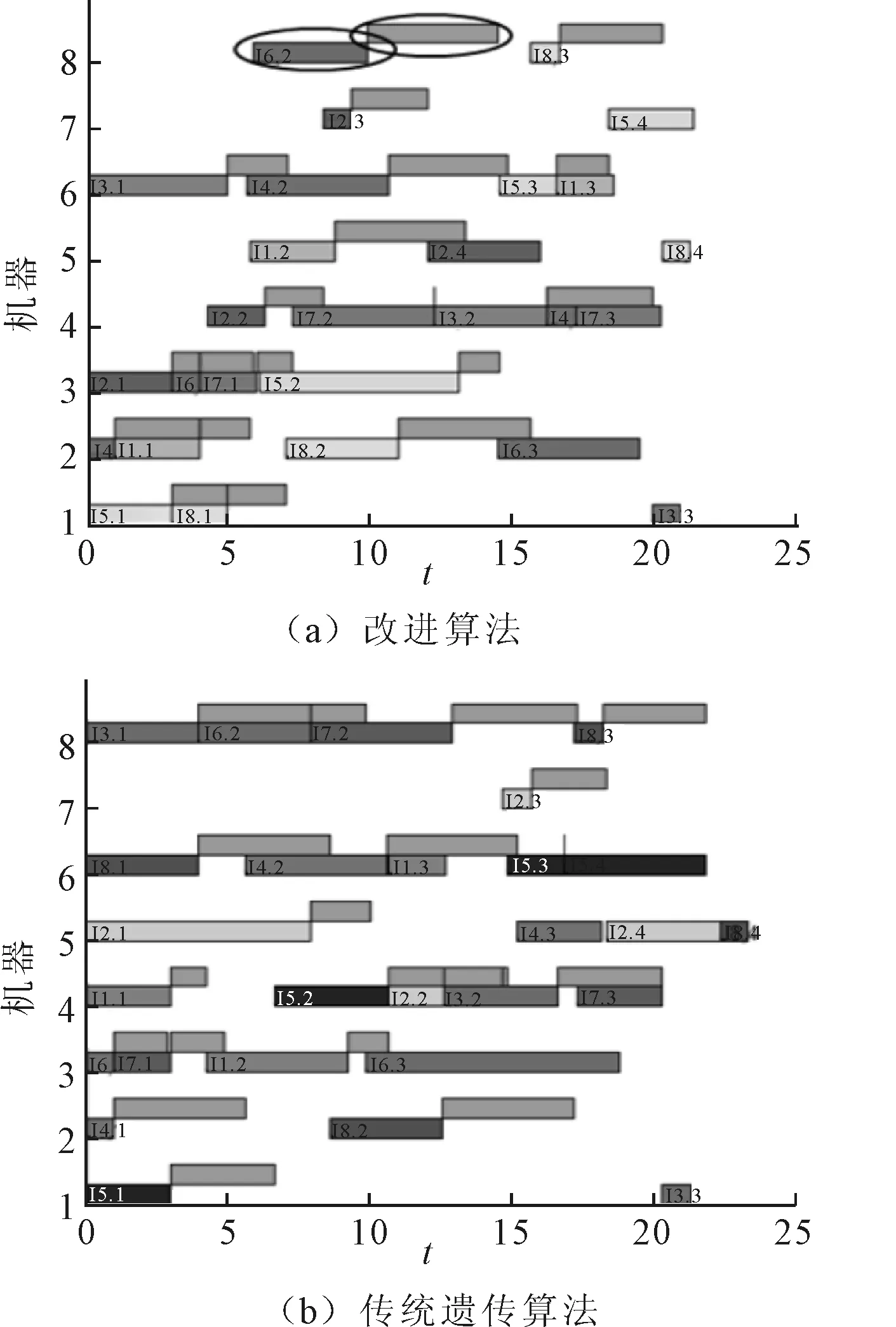
图5 调度甘特图对比(8×8P-FJSP，运输时间1～5)

该算例的调度如图5(b)所示，makespan为23.481 2，算法在求解质量上改进了9.40%。为更直观地观察改进遗传算法的收敛过程，图6给出改进算法的收敛曲线，发现由于初始化改进，算法在初期就很快找到较好的初始解。迭代前期小生境划分平衡了选择压力，曲线最优解下降速度很快。后期种群质量趋于近优解并集中到pop1，下降较为平缓，基本上在20代找到最优解，并且种群均值很接近最优解，运算质量和效率均有较大改进。

图6 改进GA-Gantt收敛曲线(8×8P-FJSP，运输时间1～5，Cmax =21.462 7)

4 结论

为实现精细化管理，提高工件响应速度，将物流业和柔性制造相融合，以柔性作业车间为背景，引入了运输时间独立时间影响因子。笔者建立了考虑运输时间的FJSP调度模型，实现了运输时间的优化；在传统遗传算法的框架下，设计了新的种群初始化方法，并引入小生境思想的局部搜索弥补GA易早熟的缺陷；编程实现了改进算法，运用标准实例测试并比较算法的性能。实验分析表明，考虑运输时间的优化调度方案更符合实际，笔者提出的小生境遗传算法与传统遗传算法相比有明显的优势。

[1] PEZZELLA F, MORGANTI G, CIASCHETTI G. A genetic algorithm for the flexible job-shop scheduling problem[J]. Computers and Operations Research,2008,35(10):3202-3212.

[2] XING L N, CHEN Y W, WANG P, et al. A knowledge-based ant colony optimization for flexible job shop scheduling problems[J]. Applied Soft Computing,2010,10(3):888-896.

[3] 贾兆红.粒子群优化算法在柔性作业车间调度中的应用研究[D].合肥：中国科学技术大学,2008.

[4] HURINK J, KNUST S. Tabu search algorithms for job-shop problems with a single transport robot[J]. European Journal of Operational Research,2005,162(1):99-111.

[5] HURINK J, KNUST S. Makespan minimization for flow-shop problems with transportation times and a single robot[J]. Discrete Applied Mathematics,2001,112(1/3):199-216.

[6] 李峥峰.多时间因素作业车间调度问题的研究与工程应用[D].武汉：华中科技大学,2010.

[7] 王永峰,王盛,李浩,等.含运输时间的柔性作业车间调度问题研究[J].科学技术与工程,2010,10(9):2216-2219.

[8] ZHANG Q, MANIER H, MANIER M A. A genetic algorithm with tabu search procedure for flexible job shop scheduling with transportation constraints and bounded processing times[J]. Computers and Operations Research,2012,39(7):1713-1723.

[9] 赵宁,李开典,田青,等.考虑运输时间柔性作业车间调度问题的快速寻优方法[J].计算机集成制造系统,2015,21(3):724-732.

[10] 王凌.车间调度及其遗传算法[M].北京：清华大学出版社,2003：13-19.

[11] 张超勇.基于自然启发式算法的作业车间调度问题理论与应用研究[D].武汉：华中科技大学,2006.

[12] 金菊良,杨晓华,丁晶.标准遗传算法的改进方案：加速遗传算法[J].系统工程理论与实践,2001,21(4):8-13.

[13] KACEM I, HAMMADI S, BOME P. Approach by localization and multi-objective evolutionary optimization for flexible job-shop scheduling problems[J]. IEEE Transactions on Systems Man and Cybernetics Part C,2002,32(1):1-13.

[14] KACEM I, HAMMADI S, BOME P. Pareto-optimality approach for flexible job-shop scheduling problems: hybridization of evolutionary algorithms and fuzzy logic[J]. Mathematics and Computers in Simulation,2002,60(3-5):245-276.

YANG Lixi:Doctorial Candidate; School of Economic and Management, Fuzhou University,Fuzhou 350108, China.

Research on Flexible Job-shop Scheduling Problem with Transport Time Consideration

YANGLixi，YUHuihui

In actual production, transport time always accounted for a large proportion of entire processing time.In order to study the flexible job shop scheduling problem more reasonably, the transportation time is considered as the independent influence factor. Aiming at the particularity of the model and the shortcomings of the traditional genetic algorithm, the niche habitat and the adaptive distance variable are used to divide the population and co-evolution, so as to balance the population selection pressure and avoid the premature convergence to the local optimum. At the same time, the method of the shortest working time is proposed to optimizing the initial population, then improve the solution efficiency of the algorithm. Using Matlab to test the common international example and compare it with the classical genetic algorithm,the results show that the proposed algorithm on this issue can get a more optimal scheduling scheme.

flexible job-shop scheduling; transportation time; genetic algorithm; niche; selection pressure

2095-3852(2017)01-0104-06

A

2016-09-18.

杨立熙(1970-),男,福建福安人,福州大学经济与管理学院副教授；博士.

TP29

10.3963/j.issn.2095-3852.2017.01.022