田湾核电站反应堆压力容器应力强度因子研究

高 焕

(国家电投集团电站运营技术(北京)有限公司，北京 102209)

田湾核电站反应堆压力容器应力强度因子研究

高 焕

(国家电投集团电站运营技术(北京)有限公司，北京 102209)

针对田湾核电站反应堆压力容器材料构件的应力强度因子参数，分别采用了俄罗斯制定的ПНАЭГ-7-002-86方法和笔者提出的计算方法进行了计算分析与比较论证。获得了如下结论：对于相同的试验工况，提出的应力强度因子计算方法与俄罗斯ПНАЭГ-7-002-86计算方法相当，比其数值略大。这是由于考虑了裂纹尖端的塑性变形特性，从影响裂纹尖端物理场的角度提出了应力强度因子的计算方法，从而导致此计算方法更为保守安全。

田湾核电站；反应堆压力容器；应力强度因子

我国田湾核电站是基于俄罗斯的WWER1000/V320核电机组经过进一步的设计改进而得到的，该机组是AES91型压水堆核电机组[1]。截至目前，俄罗斯还没有专门针对WWER1000/V320核电站机组制定出其在役检查、缺陷验收准则的标准及规范。而核电站机组设备的在役检查与验收是关乎核电站安全质保的一个重要环节[2-4]，目前田湾核电站在役检查标准执行的尚是制造阶段的验收标准，也就是《核动力装置设备和管道焊接接头和堆焊的检验规程》。该规程并未完全针对田湾核电站的设计进行检验验收标准的制定，尚存在空白验收区域。因此，需要结合俄罗斯检验验收标准，制定适宜于田湾核电站的在役检查验收准则。

由于核反应堆压力容器是核电工程机组的重要设备，其制造涉及到了大量的钢材属性、焊缝类型等材质与工艺[5-6]，因此笔者以田湾核电站机组核心组件——核反应堆压力容器作为研究对象，遵照俄罗斯现有的检测方法，论证适宜于田湾核电站的应力强度因子计算方法，以期为该压力容器的可靠性与安全性评估提供理论依据[7]。

1 应力强度因子的拟定

传统的材料破坏准则越来越不能适应于工程的实际需要。如采用最大拉应力强度破坏准则来判断材料的安全与否，并不能够满足实际需求。这是因为上述材料在当初设计的时候往往是满足于传统的破坏准则的，但是随着设备服役，还是引起了设备材料构件的失效。继而，随着大型飞机失事、钢铁厂铸造炉发生突然爆裂等意外情况的大量发生，材料工程师意识到，仅仅依靠传统的破坏准则是不够的。而材料的安全性与可靠性主要依靠其强度、变形等工程特性参数，经过仔细分析，发现材料中含有众多微小裂纹及宏观大裂纹，材料的失效是由于这些裂纹的扩展而引起的，因此，从研究裂纹如何萌生、扩展、贯通，直至宏观破坏这个角度，衍生发展了断裂力学。

断裂力学针对材料破坏，提出了新的判定准则，并对断裂韧性参数如何确定提出了全新的实验方法。进一步研究发现，材料的断裂韧性取决于多种因素，不一而述。具体到核电站反应堆，有核电站运营期间放射的热量、机组运行时散射的热量、压力容器内部温度变化导致的脆断等因素都对材料构件的断裂性质有重大的影响，这其中就涉及到了应力强度因子与断裂韧性这两个参数。在断裂力学中，往往采用应力强度因子来度量材料构件裂纹尖端的物理场强弱。但是应力强度因子的计算方法众多，因此笔者以哪一种应力强度因子计算方法对田湾核电站机组反应堆压力容器更适宜为着力点，对其安全性进行分析研究。

1.1应力强度因子与断裂韧性关系

应力强度因子KΙ是衡量材料构件内部含有裂纹尖端物理场强弱的力学参数，该值越大，表明裂纹尖端的应力强度因子越大，裂纹越容易扩展延伸。如果KΙ达到一个临界值，裂纹就会失稳扩展，导致材料构件的破坏。而这个临界值，称为材料构件的断裂韧性，其是材料构件自身的固有属性，表明材料构件阻止内部裂纹扩展的能力大小。断裂韧性值越大，裂纹越难以扩展。

从上述论述可得含裂纹材料构件的破坏准则，即断裂准则为：

KΙ≤KΙc

(1)

其中，KΙc为材料构件自身的断裂韧性。如果KΙ小于KΙc，材料构件不会破坏；如果KΙ大于KΙc，材料构件会失稳扩展直至破坏。

在断裂力学概念中，应力强度因子的表达式一般可表述为：

(2)

式中：σ为无缺陷材料构件该处的应力水平；a为构件内部裂纹的尺寸大小，此处认为是扁平椭圆形裂纹的长度；Y为材料形状与裂纹尺寸的修正系数，该值往往与裂纹尺寸、裂纹形状、材料构件的几何尺寸及材料与裂纹的边界条件等几何因素相关。

根据断裂力学理论，不同尺寸、不同形状、不同物理力学特性、不同内部裂纹大小，会有众多不同的应力强度因子计算公式。笔者对俄罗斯ПНАЭГ-7-002-86中关于裂纹尖端应力强度因子的计算进行分析，同时结合笔者提出的应力强度因子计算方法，系统论证所提出的计算方法是否适用于我国的田湾核电站。

1.2俄罗斯ПНАЭГ-7-002-86中有关应力强度因子的计算方法

俄罗斯ПНАЭГ-7-002-86中总结了大量材料构件的应力强度因子计算方法。归纳总结其对球形、锥形、筒形、椭圆形和平板形材料构件的应力强度因子计算公式为：

(3)

Mp=1+0.12(1-a/c)

Mq=1-0.64a/h

式中:Mp为由裂纹尖端附近塑性变形引起的修正；Mq为考虑自由表面影响的修正；Q为考虑壁厚影响的修正；η为应力集中系数；a为表面裂纹的深度；2c为裂纹长度；σp为拉应力分量；σq为弯曲应力分量；h为能够保持正弯曲应力分量的长度。

1.3笔者提出的应力强度因子计算方法

结合俄罗斯体系提出的MP108.7-86、M-02-91、РДЭО0330-01标准[8-10]，笔者从中选择合适的裂纹及构件形状，提出了应力强度因子计算公式。

定义 裂纹深度最大处记为A点，在堆焊层和焊缝交界处的裂纹记为B点；A点和B点的中点处记为C点；A点、B点和C点的法向应力σA、σB和σC可通过ANSYS模拟计算得到，表面裂纹应力强度因子计算点分布图如图1所示。

图1 表面裂纹应力强度因子计算点分布图

如果不考虑堆焊层的表面裂纹，其应力强度因子为：

KIA=σKAYAa1/2

(4)

KIB=σKBYBa1/2

(6)

YB=[1.1+0.35(a/s)2]·(a/c)1/2·YA

(7)

其中，s为壁厚。

如果考虑堆焊层的表面裂纹，其应力强度因子计算方法可分为以下3种情况：

(1)应力不变，壁厚为常量。

σKA=σKB=σA=σB

(8)

(2)应力沿壁厚线性分布。

σKA=0.61σA+0.39σB+

(9)

σKB=0.18σA+0.82σB

(10)

(3)应力沿壁厚抛物线分布。

σKA=0.111(3σA+σB+5σC)+

(11)

σKB=0.64σB+0.36σC

(12)

2 应力强度因子于田湾核电站的适宜性分析

俄罗斯ПНАЭГ-7-002-86提出的应力强度因子计算方法，使用了一个假定，也就是假定裂纹尖端区域为线弹性断裂区域，无塑性变形。通过拉应力与弯曲应力作用于材料构件及裂纹面上。而笔者提出的应力强度因子计算方法，考虑了裂纹尖端不同压力水平作用下致使裂纹扩展的分量叠加因素，可在裂纹形状参数中反映出来。笔者将通过示例分析所提出的应力强度因子计算方法与俄罗斯ПНАЭГ-7-002-86应力强度因子计算方法的差异性。

计算示例参数如下：压力容器壁厚为0.2m，容器外径为4m，设计压力为17.50MPa，对应的内表面裂纹最大深度为50mm，裂纹长度为300mm。设定裂纹为一锐利裂纹，并且其方向垂直于最大应力方向。截面厚度介于100～300mm，裂纹深度介于25～75mm，裂纹长度介于150～450mm。压力容器内水压试验取1.5倍的设计压力，即为26.25MPa。

由于容器筒壁所受压力为轴向对称的受力情况，根据线弹性力学理论则有：

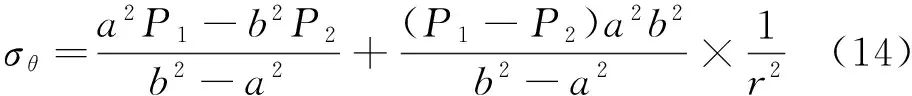
同时，筒壁上任意一点的径向位移也可通过线弹性力学理论获得：

(15)

若P1=p，P2=0，则可得：

(16)

图2所示为表面裂纹计算模型。点1为裂纹最深处，点2为堆焊交接处，裂纹长度为L。对于俄罗斯ПНАЭГ-7-002-86中的应力强度因子计算方法而言，表面裂纹中点1的计算结果为：

图2 表面裂纹计算模型

(17)

(18)

可得点1相应的拉应力分量与弯曲应力分量分别为：

通过式(3)计算可得，KI=94.29 MPa·m1/2。

采用笔者提出的应力强度因子计算方法，依据相同的水压试验及设计压力校核(26.25 MPa)，可获得相同的径向压力与切向压力值。

结合断裂力学计算原理及式(2)，对图2表面裂纹中点1的计算公式为：

KI=σKYa1/2

(19)

其中有σK=σKA，可得σK=250.05 MPa。式(19)中的形状因子YA可由式(6)确定，可得YA=1.857。从而，由式(19)计算得到，KI=σKYa1/2=250.05×1.857×0.051/2=103.80 MPa·m1/2。

从计算结果可以看出：同样的压力容器，同样的裂纹尺寸，同样的外加载荷，若采用俄罗斯ПНАЭГ-7-002-86给出的应力强度因子计算方法，可得其应力强度因子为94.29 MPa·m1/2；采用笔者提出的应力强度因子计算方法，其应力强度因子为103.80 MPa·m1/2。两者相差不大，笔者提出的计算方法所获得的数值较俄罗斯ПНАЭГ-7-002-86提出的方法获得数值稍稍偏大，这是由于笔者提出的计算方法考虑了引起裂纹尖端应力强度因子的塑性变形特性；通过应力强度因子不同路径的变化，裂纹尖端距离的改变，能够更为有效地计算裂纹尖端的应力强度因子。

3 结论

笔者针对田湾核电站反应堆压力容器材料构件的应力强度因子参数，分别采用了俄罗斯ПНАЭГ-7-002-86方法和笔者提出的计算方法进行了计算分析和比较论证，获得了如下结论：对于相同的试验工况，笔者提出的应力强度因子计算方法与俄罗斯ПНАЭГ-7-002-86方法相当，比其数值略大。这是由于笔者考虑了裂纹尖端的塑性变形特性，从影响裂纹尖端物理场的角度提出了应力强度因子的计算方法，从而导致笔者的计算方法更为保守安全。

需指出的是，核电站反应堆材料构件的失效判定准则是个多参量多准则多类别相互制约影响的系统工程，不仅涉及应力强度因子的判定，还涉及到断裂韧性曲线的拟定以及相关的研究工作，后续还需深入研究。

[1] MENAGER Y. ПНАЭГ-7-002-86 Technical specification for nuclear power plant equipment and piping strength[S]. Russia: National Print,1986:32-38.

[2] SIH G C. Method of analysis and solution of crack problem [J]. Mechanics of Fracture, 1981(1):3-9.

[3] PARKER A P. The mechanics of fracture and fatigue： an introduction[M].London: E & F N Spon, 1981(4):16-22.

[4] 李洪升，周承芳.工程断裂力学[M].大连：大连理工大学出版社，1990：36-62.

[5] 赵冰峰.核压力容器钢断裂韧性的概率断裂力学分析[D].北京:北京航空航天大学,2007.

[6] 俞树荣.压力容器用低合金钢的损伤与解理断裂研究[D].兰州：兰州理工大学,2005.

[7] 高焕.关于田湾核电站反应堆压力容器缺陷评价的研究[D].北京:机械科学研究总院,2006.

[8] MENAGER Y. MP108.7-86 Nuclear power plant equipment strength and stress intensity factor calculation [S]. Russia: National Print,1986:12-15.

[9] FNASER E. M-02-91 Permission calculation method of the equipment and pipe metal for the nuclear power plant [S]. Russia: National Print, 1991:65-68.

[10] FNASER E. РДЭО0330-01 Calculation for the equipment and pipe strength in РБМК、ВВЭР and ЭГП during the operation time [S]. Russia: National Print, 2001:77-79.

GAO Huan:Engineer; State Power Investment Group Power Plant Operation Technology (Beijing) Co., Ltd, Beijing 102209, China.

Research on the Stress Intensity Factor of Tianwan Nuclear Power Plant Reactor Pressure Vessel

GAOHuan

According to the stress intensity factor parameters of reactor pressure vessel material components of Tianwan Nuclear Power Station, the calculation and analysis of the method of ПНАЭГ-7-002-86 developed by Russia and the calculation method are carried out respectively. The results are as follows: for the same experimental conditions, the calculation method of stress intensity factor is equivalent to that of Russia ПНАЭГ-7-002-86, which is slightly larger than its value.This is due to the consideration of the plastic deformation characteristics of the crack tip and the calculation method of the stress intensity factor from the point of view of influencing the physical field of the crack tip, leading to a more conservative and safe calculation method.

Tianwan nuclear power plant; rector pressure vessel; stress intensity factor

2095-3852(2017)01-0050-04

A

2016-08-27.

高焕(1982-)，女，黑龙江哈尔滨人，国家电投集团电站运营技术(北京)有限公司工程师.

X591

10.3963/j.issn.2095-3852.2017.01.011