曲率半径对环形聚能装药侵彻深度的影响

曹 涛，顾文彬,刘建青，王振雄，徐景林，刘 欣

(解放军理工大学 野战工程学院,南京 210007)

【装备理论与装备技术】

曲率半径对环形聚能装药侵彻深度的影响

曹 涛，顾文彬,刘建青，王振雄，徐景林，刘 欣

(解放军理工大学 野战工程学院,南京 210007)

模拟了5种不同曲率半径ASC射流成型与侵彻半无限靶的过程，提出了ASC射流侵彻“三区域”理论，定义了ASC切割能力；研究结果表明：ASC在不同的位置具有不同的射流成型状况和靶板侵彻深度；不同曲率半径ASC侵彻深度均呈现明显区域特征，分别为曲率敏感区、稳定侵彻区、侵彻加强区；稳定侵彻区“平台高度”可作为ASC切割能力，但应高度重视小曲率半径ASC曲率敏感区侵彻深度；本模型中，曲率半径ρ大于80 mm时，ASC切割能力为稳定侵彻区“平台”高度26.5 mm。

ASC；曲率半径；侵彻；“三区域”理论

线型聚能装药(LSC)从20世纪六十年代开始广泛应用于航空航天和军事领域，其结构具有面对称性，炸药爆轰后形成薄片状射流，使目标产生线型切口，因此具有很强的定向切割能力。环形聚能装药(ASC)是在LSC的基础上发展而来的一种新型装药，用于在目标上快速切割预定直径的圆洞。ASC装药和金属药型罩以环形对称面为界分为外侧和内侧两个部分。内外侧对应半径不同，外侧装药质量与药型罩质量均大于内侧，故ASC结构具有不对称性，从而导致射流成型与侵彻性能相比LSC发生较大变化。曲率半径ρ是区分ASC与LSC最直接的参数，LSC可认为ρ为无穷大。研究曲率半径对ASC侵彻深度的影响对于ASC的设计与应用具有重要的理论意义与工程价值。

针对ASC装药结构不对称问题，国内外研究者进行了大量有开拓性的理论探讨与实验研究[1-4]。李永胜等[5]优化设计了反舰导弹串联战斗部前级装药，运用LS-DYNA软件，对环形切割器药型罩材料、药型罩开口角度及起爆方式进行了优选，并通过靶板实验验证了环形切割器对靶板的侵彻毁伤效果。段嘉庆等[6]根据两壁微元压垮加速度曲线，设计了内壁质量小于外壁质量，但内壁厚大于外壁厚的药型罩模型，改进了射流成型与偏斜问题。黄群涛等[7]通过对环形药型罩及其装药结构的合理匹配，解决了环形药型罩翻转成型过程中的偏斜飞散问题，并且进行了45号钢的侵彻模拟计算。吴建宇等[8]研究了炸高对于环形聚能射流侵彻特性的影响，重点分析了不同炸高下射流形态变化及侵彻切口截面形状。上述研究或是通过优化设计来改善ASC射流成型与侵彻性能，或是寻求解决射流偏斜的新途径(而这些途径往往工程上很难实现)，或是借助LSC的研究方法，讨论炸高对ASC侵彻能力的影响。目前，从等壁厚楔形罩ASC结构特点出发，研究曲率半径这个主要特征参数对其侵彻深度的影响国内外还未见报道。

基于此，本研究在控制装药截面形状与炸高相同的情况下，借助LS-DYNA有限元软件建立五组不同曲率半径的ASC 3D模型，模拟出不同大小ASC射流成型及侵彻45#钢半无限靶板的过程，旨在探寻曲率半径对ASC侵彻能力的影响规律，为后续研究工作和工程实践提供参考。

1 建模与参数验证

1.1 材料基本参数

装药采用B炸药，用高能炸药材料模型High_explosive_burn描述，炸药爆轰过程采用燃烧反应率乘以高能炸药的状态方程控制炸药化学能的释放。计算时B炸药的C-J系数和JWL状态方程参数参见文献[9]。

应用LS-DYNA软件仿真聚能效应时,只要材料参数得当，药型罩的材料模型选择Johnson-Cook或者Steinberg都能很好地模拟聚能射流的形成过程[10]。紫铜药型罩材料采用Steinberg材料模型和Gruneisen状态方程，具体参数参见文献[10]。

空气采用空物质模型，与Gruneisen状态方程连用。假设空气介质为无粘性的理想气体，爆炸波的膨胀过程为绝热过程。具体参数参见文献[11]。

45#钢靶板采用Johnson-cook材料模型和Grüneisen状态方程[12]。Johnson-cook材料模型采用乘积关系描述应变、应变率和温度对应力的影响关系，其具体形式为

(1)

1.2 建模说明

模型由炸药、金属药型罩、空气和靶板4部分构成，均采用Solid164三维实体单元。炸药、药型罩和空气采用欧拉网格，靶板采用拉格朗日网格。在模拟计算中为了防止单元大变形引起计算终止，采用多物质ALE算法。为了研究ASC射流侵彻半无限靶板的能力，模型中对空气域外围、靶板外围与底部设置无反射边界条件。

理论上ASC采用圆周环向起爆方式能够获得更好的射流成型效果，也有研究人员提出实现环形起爆的方法[13]，其基本方式是通过在环形切割器顶部覆盖圆饼状传爆药块，单点起爆传爆药块中心，实现环向同时起爆。这种起爆方式对传爆药块和ASC相对位置的加工工艺要求非常高，并且在ASC曲率半径较大时，用于起爆的传爆药量大大增加，造成了不必要的浪费和切割器重量增加。本研究综合考虑工程实际和ASC结构特点，采用截面中心两点对称同时起爆方式。

1.3 参数验证

为了验证上述参数及算法的合理性，根据文献[13]对内外罩等壁厚ASC进行的侵彻试验，建立相同工况的模型。数值模拟与实验结果对比如表1所示。

表1 数值模拟结果与实验对比

在上述条件下数值模拟的结果与实验结果具有较好的一致性，靶板下侧圆周线穿透率误差为4%，说明数值模拟材料参数和算法是合理的。

2 计算结果与分析

2.1 环形聚能射流成型与侵彻过程

为了清楚地认识环形射流形成与侵彻靶板的过程，图1展示了曲率半径ρ=150 mm ASC药型罩和靶板1/2剖面图。t=4 μs时，在爆轰波的驱动下，药型罩开始变形。由于压垮速度不一样，罩顶部材料运动速度高于两侧罩壁，使得药型罩发生翻转，环形射流逐步形成并且不断被拉长。与线型聚能切割刀[14]类似，起爆点下方射流最先触靶，触靶前射流头部保持较高速度，并且形态也未发生明显断裂，说明炸高的选取是合理的。在考察曲率半径对ASC侵彻深度影响时，控制环形切割器截面形状一致，炸高均取40 mm。

图1 ASC射流成型与侵彻靶板过程

射流触靶后对靶板的侵彻过程为一般聚能射流破甲过程，主要分为3个阶段：

1) 开坑阶段：也就是破甲的开始，从射流头部触靶到射流在靶板中建立高温、高压、高应变区。

2) 准定常阶段：射流的能量分散缓慢，破甲参数变化不大，是射流稳定侵彻的阶段，大部分孔深都属于此阶段。

3) 终止阶段:射流速度下降，靶板强度作用逐步体现出来，最终导致侵彻终止。

所不同的是轴对称聚能装药射流速度竖直向下，而ASC射流存在径向速度。图2为环形射流头部触靶前径向速度分布。其中圆心角θ=0°对应起爆点截面，θ=90°对应两起爆点对称面。径向速度表征射流偏斜的程度，从图2能够看出环形射流在各截面偏斜程度不一，起爆点截面射流向内偏斜；随着θ的增大，射流头部逐步摆正并且向外偏斜。偏斜最严重的地方发生在起爆点对称面。由于环形射流各截面射流速度参数和形态不一样，导致ASC不同圆心角θ处靶板侵彻情况不同。研究ASC侵彻深度影响规律时，必须研究靶板侵彻深度环向变化情况。

图2 ASC射流头部径向速度分布

2.2 环形聚能装药侵彻“三区域”

在考察ASC射流侵彻能力时，建立五组数值计算模型，曲率半径ρ分别为50 mm、100 mm、150 mm、200 mm、250 mm。侵彻45#钢半无限靶的深度随着圆心角θ的变化规律如图3所示。ρ=50 mm时，ASC在起爆点截面侵彻深度最小，为22.9 mm，随着圆心角θ的增大侵彻深度逐步增大。在圆心角θ=34°处侵彻深度稍有减小后稳定在26.6 mm，这段相对稳定的侵彻区域持续到圆心角θ=88°，最后在起爆点对称面侵彻深度再次增大。ρ=100 mm和ρ=150 mm两种ASC侵彻深度随圆心角θ变化规律相同，靶板侵彻深度先增大后减小，中间有较大一段侵彻深度变化较小的区域。在起爆点对称面附近，侵彻深度再次增大。ρ=200 mm和ρ=250 mm时，ASC侵彻半无限钢靶的深度环向变化规律为先减小后稳定，在起爆点对称面处侵彻深度再次增大。

根据不同曲率半径ASC射流侵彻深度环向变化规律，可将ASC分为3个区域：曲率敏感区、稳定侵彻区、侵彻加强区。曲率敏感区：在0°～40°附近，不同曲率半径ASC侵彻靶板深度呈现较大差异。从图3中看出曲率半径越大，对应侵彻深度越大。从ASC射流成型机理来看，曲率半径越大，ASC微元内外侧结构差异越小，射流偏斜对于侵彻能力的影响也就越小，故侵彻深度增加。起爆点截面ASC侵彻半无限靶结果如图4所示。

图3 不同曲率半径ASC侵彻深度

图4 起爆点截面ASC射流侵彻深度变化

稳定侵彻区：五条侵彻深度分布曲线有一段共同相交的“平台”，“平台”对应圆心角θ的范围大致是40°～80°，侵彻深度26.5 mm。稳定侵彻区的存在使得研究更加具有意义。所有计算模型均保持相同的截面形状与尺寸,并且设置相同炸高，有理由推断稳定侵彻区的“平台”高度是由ASC截面形状决定的。为了验证这种猜想，将截面高宽比由1.3调整为1.1，并进行模拟计算，发现稳定侵彻区依然存在，只是“平台”高度由-26.5 mm升为-25.1 mm。

侵彻加强区：稳定侵彻区之后各曲率半径的ASC侵彻深度均有不同程度的提高，侵彻加强区范围在80°～90°。由两个起爆点发出的爆轰波经过不同路径分别到达起爆点对称面，爆轰波的碰撞叠加使得作用于药型罩的压力明显增大，射流速度有所提高。但是，侵彻加强区ASC侵彻深度与曲率半径并未呈现明显规律，起爆点对称面侵彻深度随曲率半径变化规律如图5所示。主要原因在于此区域ASC内外侧装药爆轰存在明显的时间不同步性，导致药型罩压垮碰撞不稳定，尽管此区域射流速度有较大程度的提高，但射流形态不稳定性也十分明显。因此，该区域侵彻能力有所加强，侵彻深度存在一定不确定性。

图5 起爆点对称面ASC射流侵彻深度变化

2.3 环形聚能装药切割能力

ASC作为一种在目标上开洞的切割工具，其可靠性主要取决于使靶板脱落的最小靶板厚度，若靶板只是部分穿透而并未脱落，则认为切割器切割能力不够。因此，研究ASC最小穿深具有十分重要的实际意义。从模型计算结果来看，口宽40 mm的ASC最小穿深均超过20 mm，其中小曲率半径ρ=50 mm ASC最小穿深22.9 mm，发生在侵彻敏感区。其他四组不同曲率半径ASC靶板最小穿深均在26.4 mm左右，发生在稳定侵彻区。对于相同截面ASC，考察其切割能力时，不防将稳定侵彻区的侵彻深度作为其切割能力，这样曲率半径不是影响ASC切割能力的主要因素。但是，曲率半径较小时，其曲率敏感区侵彻深度达不到切割能力，在设计和使用过程中应高度重视。具体针对本模型，曲率半径ρ≥80 mm时，可认为稳定侵彻区侵彻深度即为ASC切割能力。图6为ρ=80 mm ASC射流侵彻深度分布，曲率敏感区最小穿深均大于稳定侵彻区。

表2 最小穿深分布情况

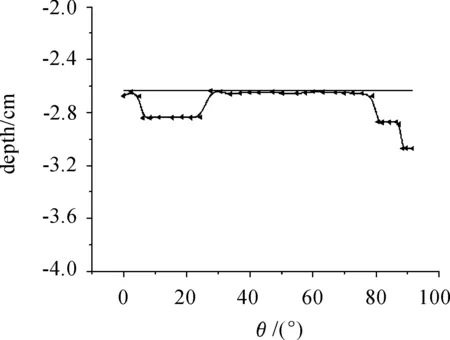
图6 ρ=80 mm ASC侵彻深度分布

3 结论

模拟出不同曲率半径ASC射流侵彻半无限钢靶板过程，发现ASC不同圆心角处射流成型状况不同，靶板侵彻深度随着圆心角的不同也发生改变。不同曲率半径ASC侵彻能力均呈现明显的区域特征。在圆心角θ为0°到40°附近，曲率敏感区侵彻深度随曲率半径增大呈现增大的趋势。40°到80°附近，射流侵彻深度稳定在26.5mm左右，不随曲率半径变化，称为稳定侵彻区。80°到90°附近，由于爆轰波的碰撞叠加作用，射流侵彻能力增强，但呈现不确定性。可将射流稳定侵彻区“平台”高度作为ASC切割能力，但在曲率半径较小时，其曲率敏感区侵彻深度达不到切割能力，在设计和使用过程中应高度重视。本研究模型中曲率半径ρ≥80 mm时，可认为稳定侵彻区侵彻深度即为ASC切割能力。

[1] BROWN J,CURTIS J P,COOK D D.The Formation of Jets from Shaped Charges in the Presence of Asymmetry[J].Journal of Applied Physics,1992,72(6):2136-2143.

[2] AYISIT O.The Influence of Asymmetries in Shaped Charge Performance[J].International Journal of Impact Engineering,2008,35(12):1399-1404.

[3] 傅磊，王伟力，吕进.环型与线型聚能装药射流成型机理对比[J].海军航空工程学院学报，2014，29(5):470-473.

[4] 王成，宁建国，卢捷.环形射流形成与侵彻的数值方法研究[J].北京大学学报，2003，39(3)：316-321.

[5] 李永胜，王伟力，刘晓红.串联战斗部前级的环形切割器优化设计[J].工程爆破，2011，17(4):1-4.

[6] 段嘉庆，王志军，贾耀鲁，等.环形射流成型的设计改进和数值模拟[J].弹舰与制导学报，2013，33(1):103-106.

[7] 黄群涛.环形EFP形成机理研究[D].南京:南京理工大学，2008．[8] 吴建宇，龙源，纪冲.炸高对环形聚能射流侵彻特性的研究[J].兵器材料科学与工程,2015,38(4):68-72.

[9] 时党勇，李裕春，张胜民.基于ANSYS/LS-DYNA8.1进行显示动力分析[M].北京：清华大学出版社，2005.

[10]陈文刚,张越.不同材料模型的药型罩对仿真结果的影响[J].科学技术与工程,2010,10(13):3226-3229.

[11]纪冲，龙源，唐献述.爆炸载荷下X70钢管的局部破坏效应[J].高压物理学报，2013，27(4)：567-571.

[12]陈刚，陈忠富，陶俊林.45钢动态塑性本构参量与验证[J].爆炸与冲击,2005,25(5):451-456.

[13]吴成，曾艳春，张向荣，等.环形聚能药型罩的设计新方法与实验[J].北京理工大学学报，2007,27(4)：291-294.

[14]高接东.基于变壁厚药型罩的 LEFP成型机理研究[D].南京:南京理工大学，2013．

(责任编辑 周江川)

Effect of Curvature Radius on Annular Shaped Charge Penetration Depth

CAO Tao, GU Wen-bin, LIU Jian-qing, WANG Zhen-xiong, XU Jing-lin, LIU Xin

(College of Field Engineering, PLA University of Science & Technology, Nanjing 210007, China )

The processes of ASC with 5 kind of curvature radius jet formation and penetration into half-infinite target were simulated. Three region theory of ASC jet penetration was proposed and cutting capacity of ASC was defined. Research results show that ASC presents different jet formation condition and target penetration depth in different position; ASC with different curvature radius presents evident region characteristic consistently in penetration depth, including curvature radius sensitive region, stable penetration region and penetration fortified region; ASC cutting capacity is defined by platform height of stable penetration region and much attention should be paid to small curvature radius ASC. In this model, when curvature radius isρ>80 mm, the ASC cutting capacity is platform height(26.5 mm) of stable penetration region.

ASC ; curvature radius; penetration; “three region” theory

2016-09-22；

2016-10-23

总后基建营房部重点课题(KYGYZXJK0914)

曹涛(1992—)，男，硕士研究生，主要从事爆炸作用机理和战斗部设计研究。

顾文彬(1961—)，男，教授，博士生导师，主要从事爆炸作用机理和战斗部设计等研究，E-mail：guwenbin1@aliyun.com。

10.11809/scbgxb2017.02.015

曹涛，顾文彬,刘建青，等.曲率半径对环形聚能装药侵彻深度的影响[J].兵器装备工程学报，2017(2):61-64.

format:CAO Tao, GU Wen-bin, LIU Jian-qing,et al.Effect of Curvature Radius on Annular Shaped Charge Penetration Depth[J].Journal of Ordnance Equipment Engineering,2017(2):61-64.

TJ5

A

2096-2304(2017)02-0061-04