卫星飞轮隔振系统频率漂移诱发低频共振现象*

申军烽， 周春华， 虞自飞 ， 刘 曌 ， 封淑清

(1.上海卫星工程研究所 上海,200240) (2.上海航天控制技术研究所 上海,201109)(3.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

卫星飞轮隔振系统频率漂移诱发低频共振现象*

申军烽1， 周春华1， 虞自飞1， 刘 曌2， 封淑清3

(1.上海卫星工程研究所 上海,200240) (2.上海航天控制技术研究所 上海,201109)(3.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

建立了卫星飞轮隔振系统的力学模型，研究了在弹性支撑下飞轮转动与进动共同作用下飞轮隔振系统的固有频率变化规律。通过理论分析得出，飞轮逆向进动频率与飞轮转动分频在低频段交汇，会诱发隔振系统的低频共振。进行了飞轮隔振系统的动力学试验，验证了系统的固有频率存在频率漂移现象，同时证明飞轮在高转速下会诱发系统在低频区域的共振。提出了增加系统阻尼的方法来抑制低频共振现象，试验表明，该方法可有效减缓频带漂移诱发的低频共振问题。

飞轮；飞轮隔振；频率漂移；低频共振；微振动

引 言

随着我国卫星向着高精度、高稳定性及长寿命方向发展，其搭载的敏感载荷对平台微振动环境要求越来越高，卫星平台微振动抑制问题难以回避。国外研究发现[1-2]，飞轮微振动是影响卫星有效载荷性能指标的主要因素，因此抑制飞轮引起的微振动显得十分迫切。常用的飞轮微振动控制方法[3-5]有阻尼减振、安装部位结构刚化和振源隔振等。例如，哈勃望远镜利用液体阻尼隔振器对飞轮进行隔振，有效降低飞轮转动时引发的高频振动[6]。先进X射线太空望远镜采用飞轮隔振支架抑制中高频段的振动响应[7]。詹姆斯韦伯太空望远镜采用双重被动隔振系统减小飞轮的振动影响[8]。在以往的飞轮隔振研究中，一般认为隔振系统的固有频率与飞轮的转速无关[9-10]。然而，在飞轮隔振系统的实际应用和试验中发现，飞轮在高转速的情况下经常会诱发隔振系统的低频共振。这一现象难以用原有的建模分析方法进行解释。由于低频段的共振对多数敏感载荷性能影响较大，因此对飞轮隔振系统的建模分析必须关注飞轮隔振系统固有频率与飞轮转速之间的耦合关系。

1 飞轮隔振系统建模

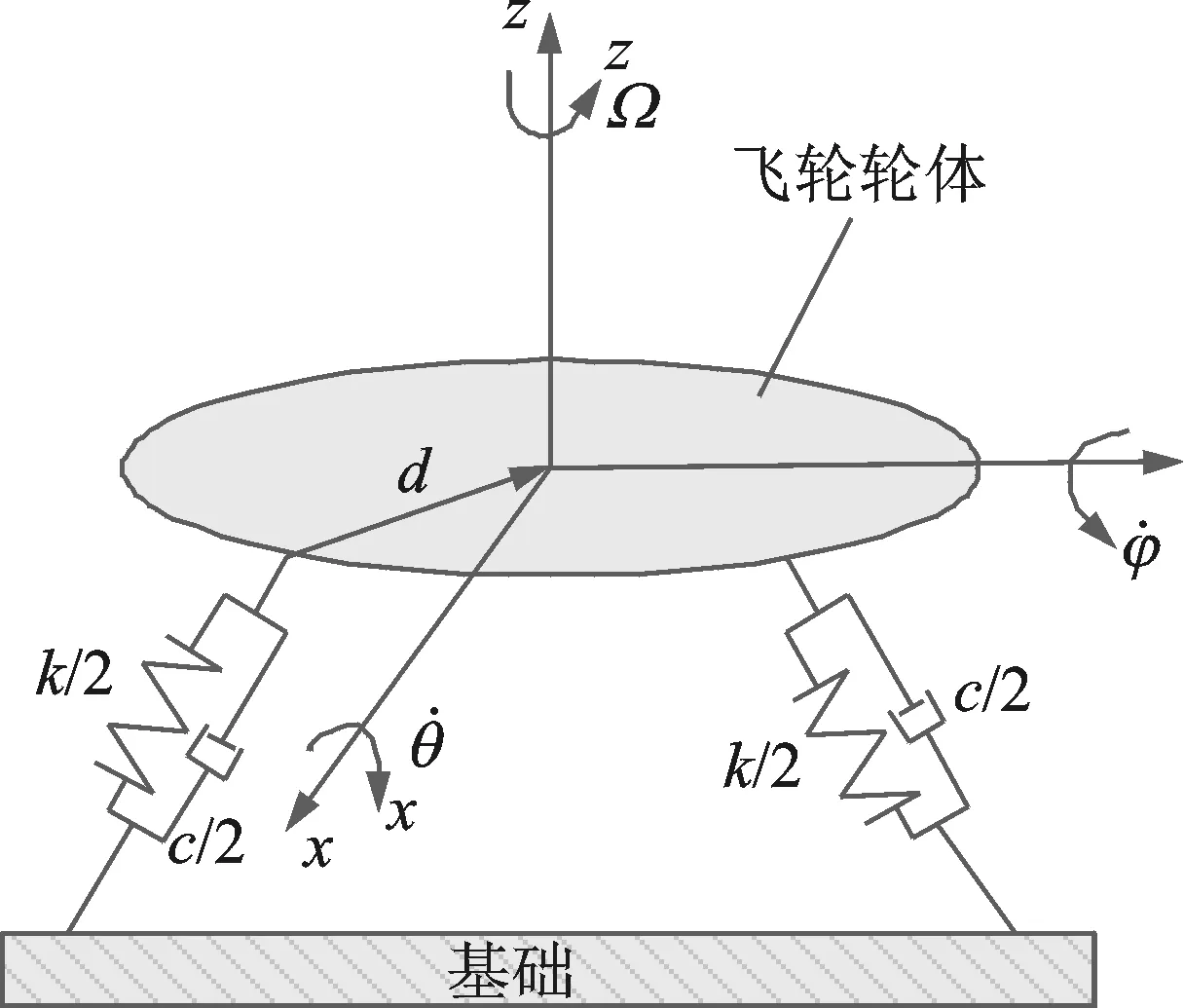
图1 飞轮隔振系统理论模型Fig.1 Theory model of vibration isolation system for flywheel

系统的动能为

系统的势能为

系统阻尼耗散能为

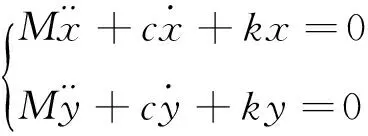
(1)

(2)

其中：kθ=kd2;cθ=cd2;θ=Aeiωt;φ=Beiωt；A，B为振幅。

假设系统为无阻尼系统，即c=0，则求解式(1)可以得到系统平动方向的固有频率ωt为

由于k和M不变，因此其平动方向的固有频率不变。

求解式(2)，得到系统转动方向的固有频率ωr为

(3)

根据式(3)，由于kθ是和转频ω(ω=Ω/60)相关的一个量，所以转动方向固有频率ωr会随着转速Ω改变。因此，飞轮隔振系统的转动自由度上出现两个随转速Ω改变的固有频率，一个随飞轮速度的增加而正向进动，一个随飞轮速度的增加而逆向进动。

2 飞轮隔振系统固有频率分析

设飞轮惯量Irr=0.1 kg·m2,Izz=0.2 kg·m2。对于10 Hz与14 Hz两种飞轮隔振系统，相应的kθ可等效为400 N/m和780 N/m，分析工况为飞轮转速从0匀速加速至5 kr/min，转动方向的固有频率变化趋势如图2，3所示。图(b)为图(a)的局部视图。分析飞轮的频谱成分[11-13]可以看到，飞轮除了转频以外，主要还包括0.6，0.22，2以及3倍频等。为简化问题，这里仅绘制飞轮的转频和0.22倍频。可以看出：

1) 隔振系统转动方向的固有频率随飞轮转动的时间变化延伸出两条频带，一个为正向进动，另一个为逆向进动，呈现V型特征。

2) 根据式(3)，飞轮转速Ω=0时，V型特征谱线的起始点为隔振系统转动方向固有频率的基频。另外，系统的刚度k越大，则转动频率的基频越高，在图中该起始点也就越靠右，反之依然。因此，支撑刚度k决定了V型特征谱线起始点的位置。

3) 由于模型中假设飞轮隔振系统的刚度只有一个支撑刚度k，因此只能得到一个V型特征谱线。实际结构中，系统的多个支撑刚度将对应多个V型谱线。

4) V型谱线中逆向进度的频带能够与转频的分频在低频区域交汇诱发低频共振。例如，14 Hz和10 Hz飞轮隔振系统的第1阶逆向进动频率与0.22倍频分别在8.9 Hz和6.4 Hz附近交汇，但此时飞轮对应的转速却为2 450 r/min(40.8 Hz)和1 710 r/min(28.5 Hz)的高转速区域。可见，由于飞轮转速与隔振系统频率存在耦合，飞轮的高速转动能够诱发系统的低频共振。

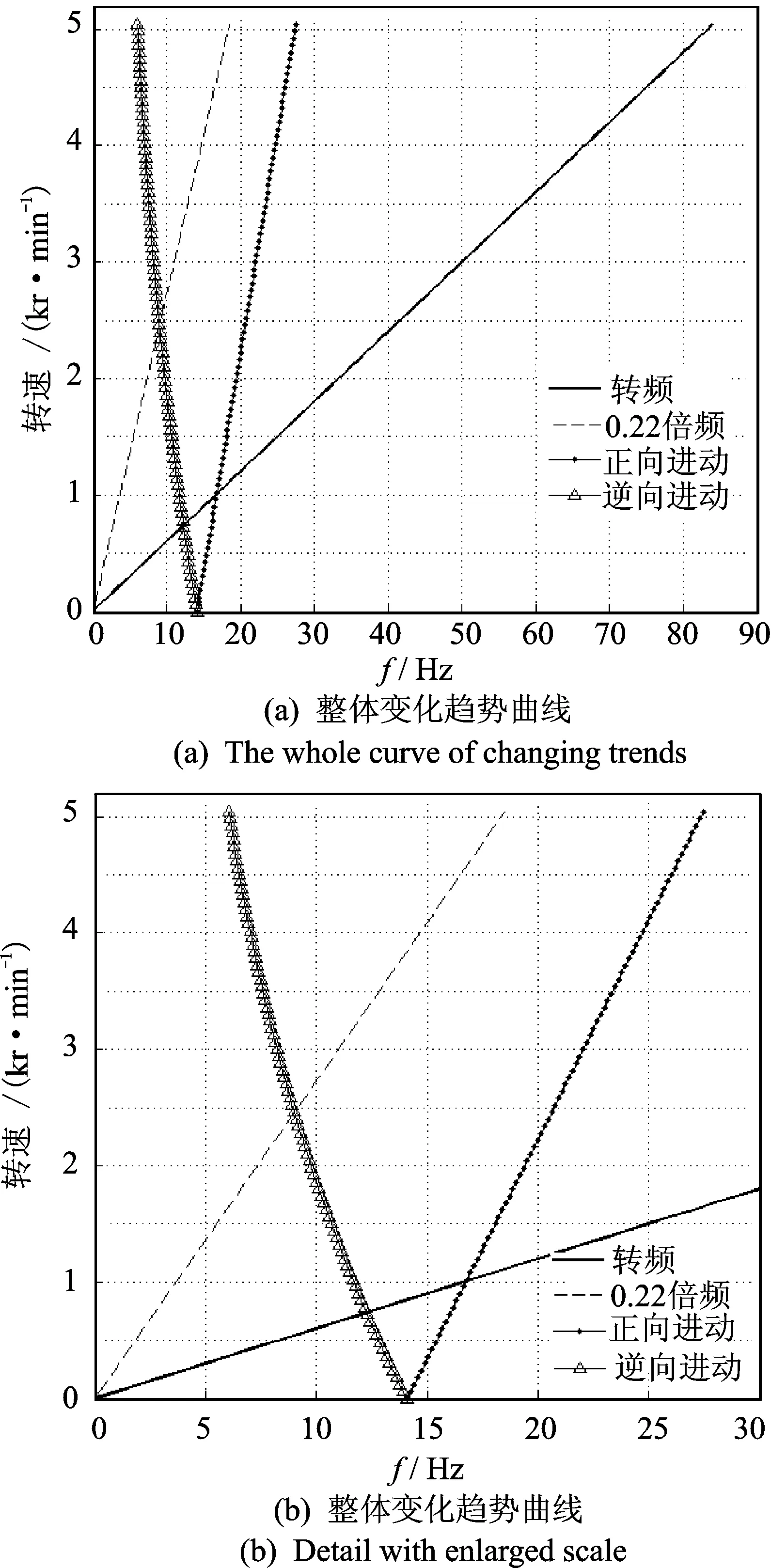
图2 14 Hz飞轮隔振系统无阻尼频谱变化Fig.2 Frequency spectrum change of vibration isolation system for 14Hz flywheel without damp

图3 10Hz飞轮隔振系统无阻尼频谱变化Fig.3 Frequency spectrum change of vibration isolation system for 10Hz flywheel without damp

3 飞轮隔振系统试验及分析

对14 Hz和10 Hz飞轮隔振系统分别进行特性试验。试验工况为飞轮转速从0匀速加速至5 kr/min，此时飞轮隔振系统振动的频谱图如图4,5所示。图中的纵坐标表示飞轮升速时间(对应于飞轮的转速)，由暗到亮的色彩表示振动响应由小到大。对比图4,5可以看出：

1) 两种飞轮隔振系统都存在明显的V型频谱特征，且由于14Hz飞轮隔振系统刚度高于10 Hz飞轮隔振系统，因此10 Hz支架的V型特征相比于14Hz支架的V型特征，整体左移。另外，由于两种飞轮隔振系统存在2个基频，因此频谱中存在2个V型频线。

2) 14 Hz飞轮隔振系统的逆向进动频带在7.7Hz附近与0.22倍频交汇共振，此时的转频为35 Hz(2 100 r/min)。10 Hz飞轮隔振系统逆向进动频带在6.1 Hz附近与0.22倍频交汇共振，此时的转频为27Hz(1 620 r/min)。这说明即使是高频振动，同样能够诱发低频共振，而多数敏感载荷对低频振动较为敏感，这一点需要重点关注。

3) 理论预测的交汇点与试验结果存在一定偏差，且隔振系统固有频率变化呈明显非线性，尤其在高频段逐渐趋向于转频的倍频。这主要是由于在系统方程中间引入小位移和小角度线性假设，同时没有考虑飞轮的不平衡量及电机控制等因素，降低了系统方程的非线性和耦合性，但并不妨碍对系统频率变化趋势的判断。

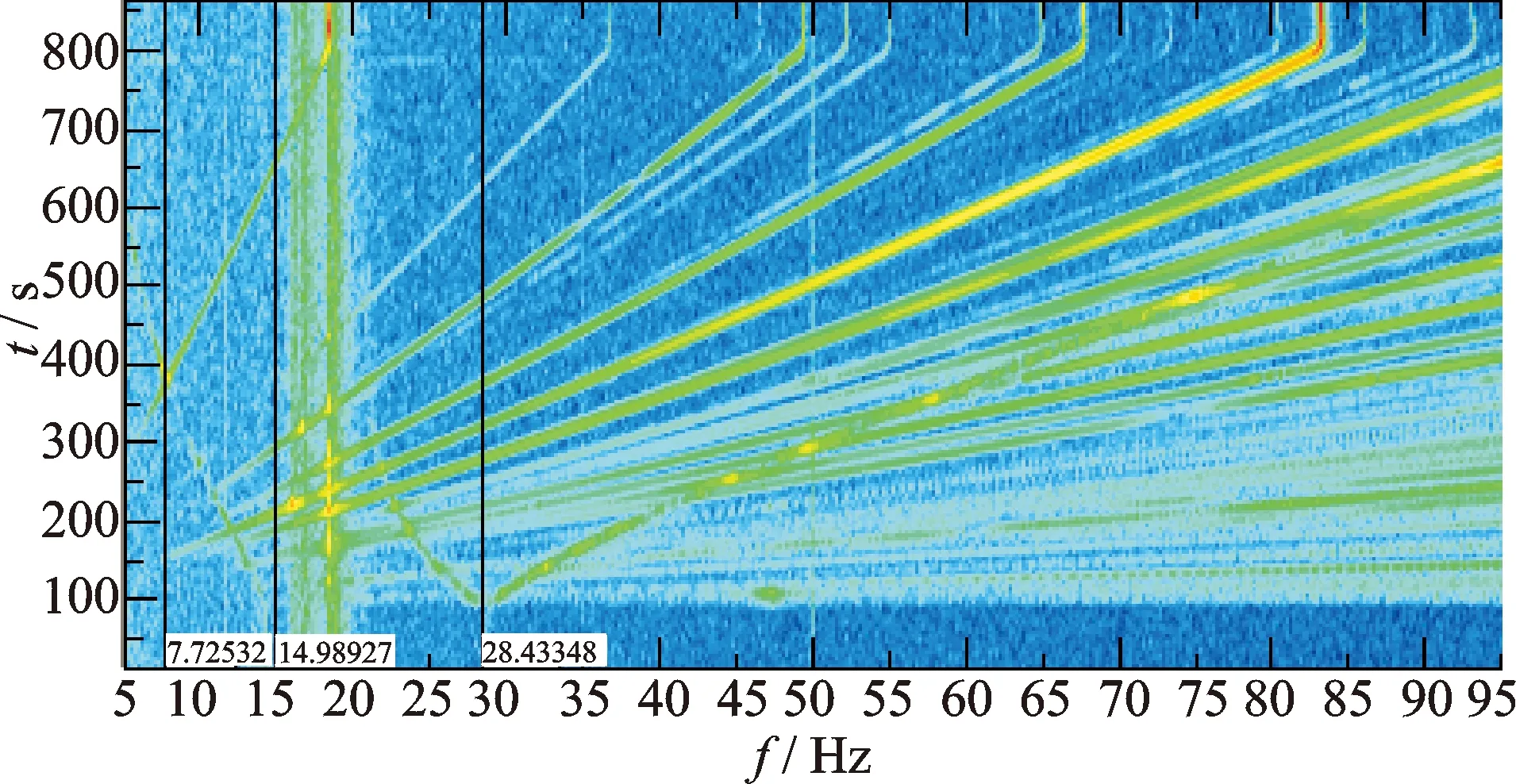
图4 14Hz飞轮隔振系统无阻尼频谱Fig.4 Frequency spectrum of vibration isolation system for 14Hz flywheel without damp

图5 10Hz飞轮隔振系统无阻尼频谱Fig.5 Frequency spectrum of vibration isolation system for 10Hz flywheel without damp

为进一步减缓飞轮隔振系统低频交汇共振的影响，一个办法是增加隔振系统的阻尼比。为此，将对两种飞轮隔振系统的一阶转动频率对应的阻尼比提升至0.05，重复上述试验，此时隔振系统相应的频谱图如图6,7所示。对比无阻尼飞轮隔振系统的频谱可以看出：增加阻尼后的飞轮隔振系统频谱中，V型频谱特征基本不明显，仅剩下飞轮自身的转频、倍频以及分频成分。这说明阻尼能够有效地抑制飞轮隔振系统与飞轮转速的耦合效应。

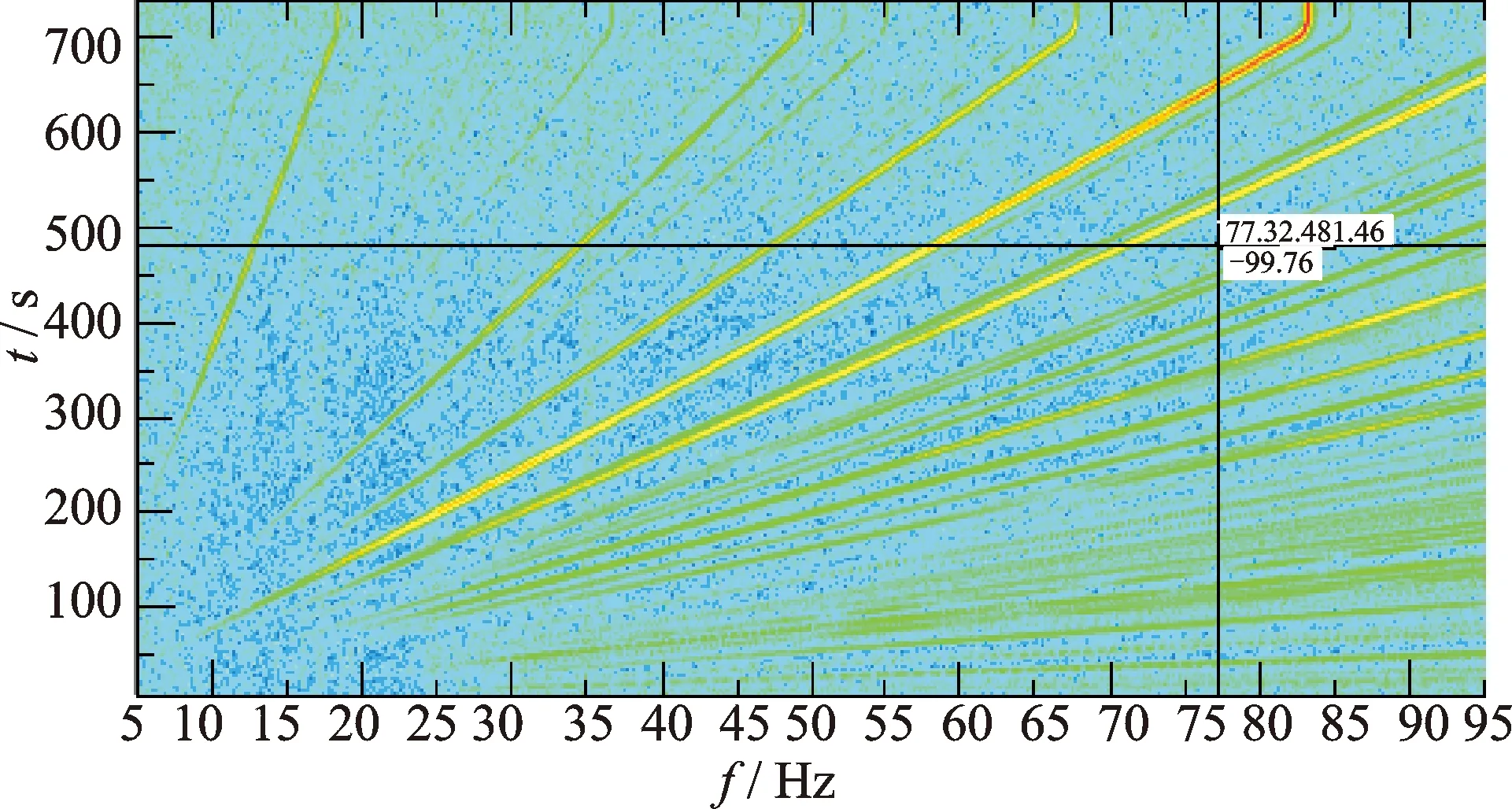
图6 14 Hz飞轮隔振系统有阻尼频谱Fig.6 Frequency spectrum of vibration isolation system for 14Hz flywheel with damp

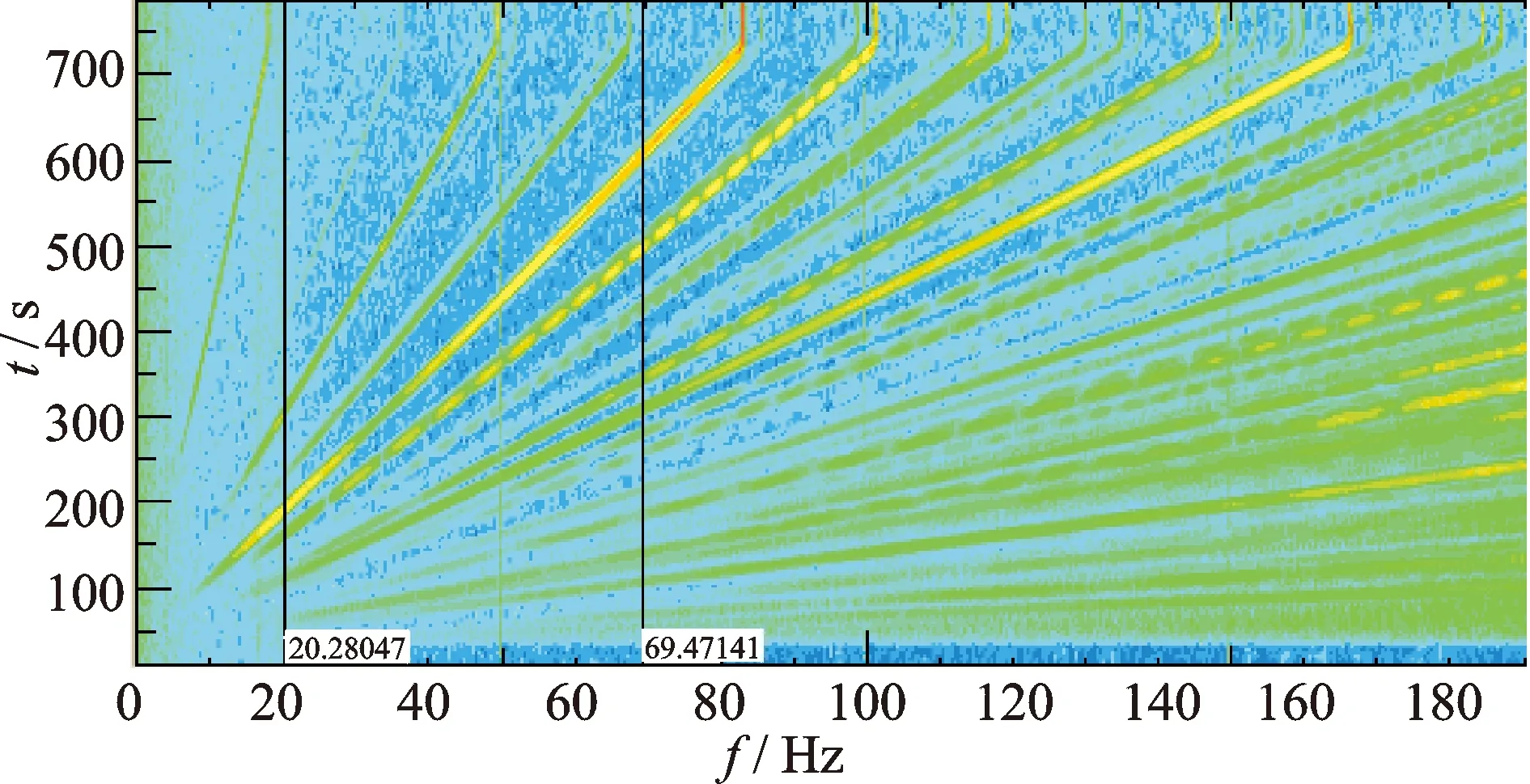
图7 10 Hz飞轮隔振系统有阻尼频谱Fig.7 Frequency spectrum of vibration isolation system for 10Hz flywheel with damp

4 结束语

理论和试验分析可知，由于存在弹性支撑，使飞轮的转动与隔振系统频率耦合，导致飞轮隔振系统的固有频率随着飞轮转速的增加、同时存在逆向进动与正向进动的特性。其逆向进动频率能够与飞轮的分频在低频段发生交汇，从而诱发低频共振。试验表明，增加隔振系统的阻尼可以有效减缓频带漂移诱发的低频共振问题。

[1] Eyerman C E, Shea J F. A systems engineering approach to disturbance minimization for spacecraft utilizing controlled structures technology[R]. Massachusetts: Massachusetts Institute of Technology, 1990.

[2] Melody J W. Discrete-frequency and broadband reaction wheel disturbance models[R]. La Canada Flintridge: Jet Propulsion Laboratory, 1995.

[3] Bronowicki A J. Vibration isolator for large space telescopes[C]∥45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference. Palm Springs, California: AIAA, 2004: 19-22.

[4] 刘天雄, 范本尧, 杨慧. 卫星飞轮扰振控制技术[J]. 航天器工程, 2009, 18(1)：53-60.

Liu Tianxiong, Fan Benyao, Yang Hui. Research on vibration disturbance control of momentum wheel[J]. Spacecraft Engineering, 2009, 18(1): 53-60. (in Chinese)

[5] Oh H U, Taniwaki S. Flywheel vibration isolation test using a variable-damping isolator[J]. Smart Material Structure, 2006，15(2)：365-370.

[6] Davis L P, Wilson J F, Jewell R E. Hubble space telescope reaction wheel assemble vibration isolation system[R]. NASA: Marshall Space Flight Center, 1986.

[7] Pendergast K J, Schauwecker C J. Use of a passive reaction wheel jitter isolation system to meet the advanced X-ray astrophysics facility imaging performance requirements[J]. NASA/CR, Astronomical Telescopes & Instrumentation,1998,3356(2):1078-1094.

[8] Bronowicki A J. Vibration isolator for large space telescopes[C]∥45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference. Honolulu, Hawaii:AIAA, 2004：45-53.

[9] 阳剑. 针对飞轮扰动的卫星减振技术研究[D]. 哈尔滨：哈尔滨工业大学, 2013.

[10] 骁麟. 航天器典型部件微振动隔离技术研究[D]. 上海：上海交通大学，2013.

[11] 王全武, 虎刚. 飞轮振动频谱特征的初步理论分析和验证[J]. 空间控制技术与应用, 2008, 34(4): 42-46.

Wang Quanwu, Hu Gang. Analysis and validation of flywheel vibration spectrum characteristics[J]. Aerospace Control and Application, 2008, 34(4): 42-46. (in Chinese)

[12] 赵煜, 张鹏飞, 程伟. 反作用轮扰动特性测量及研究[J]. 实验力学, 2009, 24(6): 532-538.

Zhao Yi, Zhang Pengfei, Cheng Wei. Measurement and study of disturbance characteristics of reaction wheel assembly[J]. Journal of Experimental Mechanics, 2009, 24(6): 532-538. (in Chinese)

[13]Liu K C, Maghami P. Reaction wheel disturbance modeling, jitter analysis, and validation tests for solar dynamics observatory[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu, Hawaii: AIAA, 2008: 1-18.

10.16450/j.cnki.issn.1004-6801.2017.01.008

机械结构力学及控制国家重点实验室开放课题资助项目(MCMS-0513K02)

2015-02-02；

2015-08-25

TH744; V414.6

申军烽，男，1979年5月生，博士、高级工程师。主要研究方向为卫星结构设计与振动控制。 E-mail:giftxin@163.com