基于实际震害的土石坝永久变形估算

楚金旺，朱 晟，黄亚梅

1 研究背景

土石坝由于其就地取材和施工比较简单，是被普遍采用的一种坝型。已有资料表明［1-4］，土石坝地震震害主要表现为震后永久变形。通过计算得到的土石坝在地震过程中发生的永久变形，成为评价其抗震稳定与安全的重要指标。

自Newmark首次引入屈服加速度的概念［5］，并提出计算由于地震作用引起刚塑性坝体有限滑移的基本思想后，一些研究者依据这一方法提出了各种算法。其中较具代表性的是Makdisi等［6］在考虑坝体为非刚性体，在对9座填筑密实、由压实的黏性土构成的土石坝进行动力反应分析，计算其地震永久变形的基础上，提出估算土石坝地震变形的简化方法。随后，Sarma［7］、Ling［8］、Jinman［9］、Yegian［10］等利用大量的地震记录和震害资料验证以前发展的理论，不断深入并加以完善。由于该类方法是建立在实际土石坝工程基础上的，其优点是简单和方便；但是，其所用的地震动记录、坝高范围、坡比等较为有限，且地震永久变形样本是通过计算得到的，因而也带有明显的局限性。Serff等［11］提出的基于应变势概念的整体变形计算方法在高土石坝抗震设计中有广泛的应用。但是，基于等价线弹性理论的动力分析方法能否合理计算土石坝的永久变形，基于室内缩尺的动力试验成果能否合理反映筑坝材料的动力特性，这些问题尚未得到震害实践的检验。

为此，本文结合土石坝工程的震害资料，分析其产生地震永久变形的可能影响因素，进而提出基于实际震害的预测方法。

2 影响土石坝永久变形的因素分析

通过土石坝实际地震的震害调查，整理已建部分大坝遭遇地震时发生的永久变形，见表1。影响土石坝永久变形的因素较为复杂，主要与筑坝材料物理力学特性、大坝结构振动特性、场地地震动特性等因素相关。

表1 已建大坝实测地震永久变形

2.1 场地地震动特性

2.1.1 地震卓越周期Tp由于坝址基岩地震动为随机过程，频率（或周期）不是常数，通常用卓越周期来表征基岩地震动时程曲线的周期性质。坝址场地地震卓越周期，采用Seed［25］关于卓越周期与震中距、震级关系的研究成果（见图1）来确定，同一震级时，卓越周期随震中距增加而增大。

2.1.2 基岩最大加速度 坝址基岩的地震加速度峰值越高，土石坝的地震反应越剧烈，其震后永久变形越大。考虑到基岩加速度峰值与坝顶加速度反应峰值有较好的相关性，本文近似利用坝顶加速度反应来反映这种影响。

2.2 大坝自振周期土石坝地震反应的大小，与地震时坝址地基和坝体耦合作用的强弱有关。对应于第一振型的自振周期为基本自振周期。在岩基上修建的土石坝，它的基本自振周期一般在0.3～1.5 s，而坚硬场地的地震加速度时程的卓越周期为0.1～0.5 s，大坝自振周期对其动力反应影响较大；当自振周期与地震动卓越周期接近或相等时，地震作用下大坝的动力反应则会急剧增大，其自振周期与场地卓越周期的关系是决定土石坝地震反应剧烈程度的关键因素。

土石坝的自振周期较为复杂，与坝高、坝坡、筑坝材料特性、河谷形状和坝基等因素有关，与大坝挡水高度也有关系。不少学者［26-28］在研究坝体自振周期时采用简化方法，主要考虑坝高的影响。

式中：Ti为第i阶自振周期，单位为s；H为坝高，单位m；ρ为材料密度，单位为kg/m3；K为常系数；g为重力加速度，单位为m/s2；为第一类贝塞尔函数的第1/（2n-1）阶根。

参考 Ghaffar［29］对 Santa Felicia坝和 Nose［30］对 Kisenyama坝进行的现场试验实测资料，取 n=3.0。

上述自振周期计算公式（1）适用于二维情况，实际土石坝自振周期还与河谷的形状有关。定义θ反映三维河谷影响［31］，即

式中：L为坝轴线长，则大坝基本自振周期修正为

为了简化起见，可将涉及材料特性的数据用函数f1(m)表示，m的取值可反映不同筑坝材料力学特性的影响，则其一阶自振周期可表示为关于m、H、L/H的函数，即

超滤膜在截留多糖的同时，也使得部分大分子蛋白质难以脱除。不同分子量的超滤膜对蛋白质的脱除效果如图2所示。

表2为收集到的部分土石坝经历地震或采用爆破试验获得的实测基本自振周期资料。根据筑坝材料特性的不同，对于均质土坝：取m=0；分区土坝：取m=1；堆石坝：取m=2。对表2的实测资料进行回归分析，得到自振周期关于m的表达式：

式中：a=0.0394，b=-0.0267，c=0.0066。

大坝一阶自振周期计算公式为：

式中 f(m)按公式5计算。

为了检验计算自振周期的精度，绘出其与实测值的对比值（见图2），可见拟合的公式（6）较为精确，采用该公式补充计算表1列出大坝所缺少的原型大坝基本自振周期。

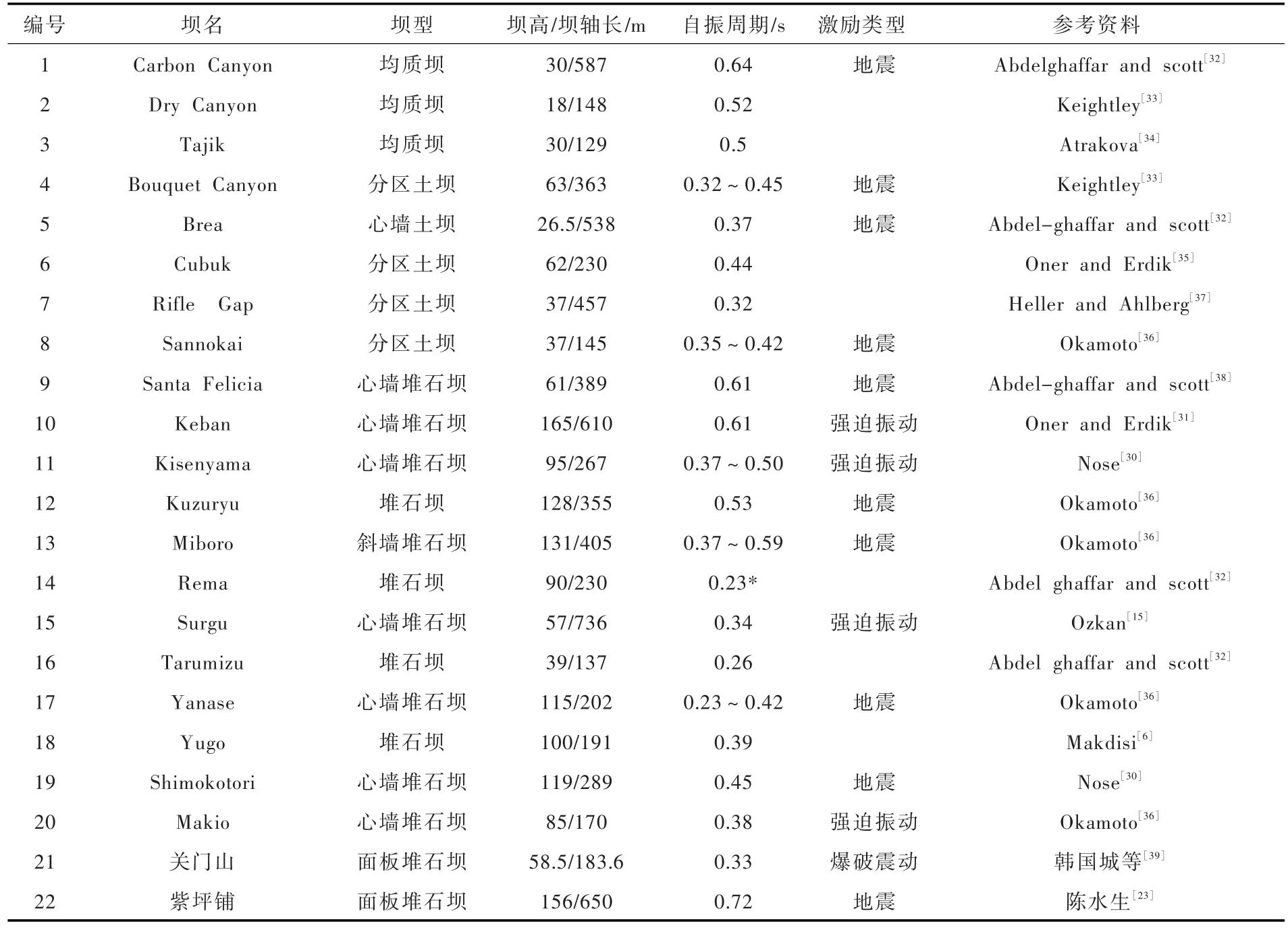
表2 实测土石坝基本自振周期

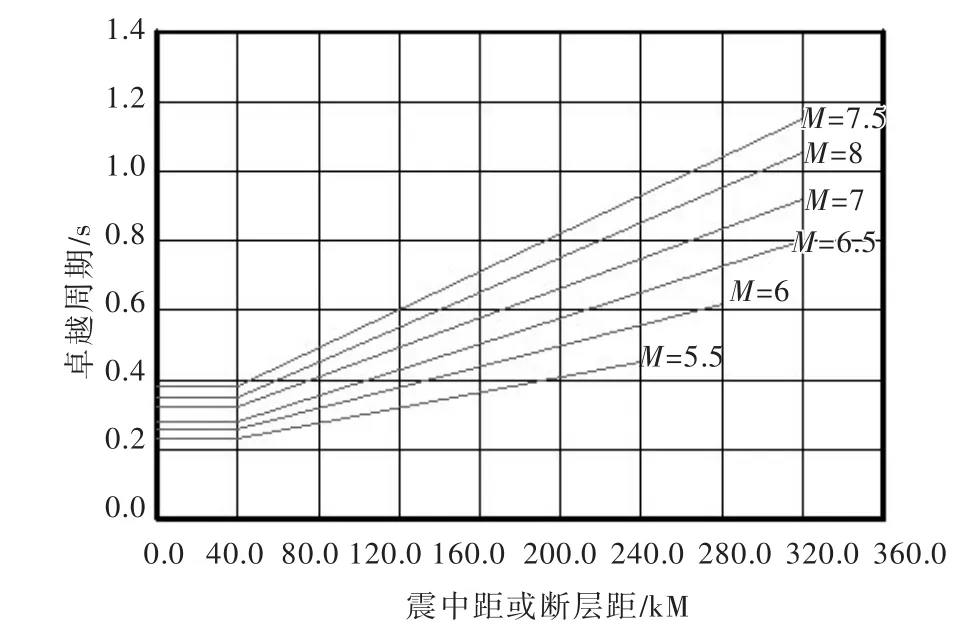
图1 坝址地震卓越周期与震级、震中距的关系

图2 实测和计算自振周期的比较

根据表1的大坝地震震害资料，得到自振周期Td与卓越周期Tp的比值和永久变形D的关系见图3。可见随着Td/Tp的增大，实测永久变形减小。但是，部分大坝的自振周期Td小于地震卓越周期Tp时，实测永久变形量值仍然较大，与一般土石坝的振动特性不符。分析原因可能是由于表2所列实测的大坝基本自振周期，是在土石坝经历微震或采用爆破试验获得的，对应大坝动力反应较小，基本接近弹性状态；而实际土石坝只有在地震反应较为剧烈时，才会产生明显的永久变形，此时筑坝材料已经出现软化现象，大坝的自振周期将进一步延长。

在地震过程中，坝体自振周期随着时间变化，且其自振周期与刚开始静态自振周期相差较大，并随着输入地震波的峰值增加而相差更大。通过对鲁布革、瀑布沟、双江口、黄金坪、天生桥和卡基娃等算例，输入不同峰值的地震波，得到坝顶加速度放大倍数与基本自振周期放大倍数关系的平均值见图4。

图3 Td/Tp对永久变形D的影响

图4 自振周期放大系数与坝顶加速度放大倍数关系

由图4可见：考虑地震中材料的软化特性，大坝的基本自振周期放大倍数Tn与坝顶加速度反应放大倍数An的关系可以用直线拟合：Tn=2.32-0.285·An，利用Tn对公式（6）的大坝基本自振周期进行修正后，得出Td/Tp与永久变形的关系见图5。

由图5可得出永久变形随着Td/Tp的增大而减小，当Td/Tp接近1.0时，大坝因共振效应而使得其地震反应较为剧烈，实测的永久变形最大。

2.3 滑块屈服加速度ay与最大加速度amax地震作用下土石坝的水平向加速度反应最大，且位置一般在坝顶，可由坝址基岩地震的最大加速度，参考《水工建筑物抗震设计规范》［40］的相关统计资料，查图6求得。考虑大坝最大加速度amax与竖向变形V以及水平变形U的关系见图7。可以看出，永久变形随着坝顶最大水平加速度的增大而增大。

图5 修正Td/Tp对永久变形D的影响

图6 大坝最大加速

图7 大坝最大加速度amax与永久变形的关系

大坝的水平向屈服加速度用下式估算［5］

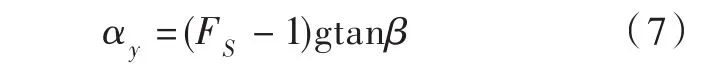
式中：FS为初始边坡安全系数，β为最危险滑动体滑坡坡角。

在计算屈服加速度时，表1部分大坝的屈服加速度直接引用文献［41］的结果，表3列出了几座典型土石坝的材料参数。

表3 典型土石坝材料参数

Ling等［41］研究认为输入竖向加速度对坝坡滑移计算结果的影响较小，计算时不考虑竖向加速度的影响。永久变形和屈服加速度与最大加速度比值的关系见图8，可看出永久变形随着ay/amax的增大而减小。

3 永久变形计算

图8 ay/amax与永久变形D的关系

根据以上对永久变形影响因素的分析，可建立永久变形的公式。

3.1 竖直向变形V 基于以上分析，自变量选取ay/amax。确定因变量：①对比图5所示大坝的竖向变形V与Td/Tp的关系曲线，采用幂函数形式对其进行拟合；②对大坝的竖向变形V与amax的关系（见图7），采用线性函数形式对其进行拟合。

根据V和Td/Tp以及amax的关系，可以确定大坝竖向变形计算的拟合公式：

式中：x=ay/amax，a、b、c、d为拟合参数，根据大坝实际测量值回归确定，其上限、下限和平均曲线的各系数值见表4，拟合曲线如图9所示。

表4 拟合曲线系数表

图9V*（Td/Tp）2.0/（amax/g）与ay/amax关系

3.2 水平向变形U与竖向变形类似，大坝的水平位移U和Td/Tp以及amax的关系，亦可采用下式拟合：

式中：x=ay/amax，a、b、c、d为拟合参数，根据大坝实际测量值回归分析确定，其上限、下限和平均曲线的各系数值见表5，拟合曲线如图10所示。

表5 拟合曲线系数

由拟合出来的公式计算表1所列的土石坝并于实测值进行比较，见图11。为便于比较，图中同时作出了Makdisi、Seed、Sarma等人建议方法的预测结果。可以看出，本文提出的永久变形计算公式更接近实测值。

图10U*（Td/Tp）2.0/（amax/g）与ay/amax关系图

图11 土石坝地震永久变形的计算预测精度

4 算例分析

双江口心墙堆石坝最大坝高312 m，坝轴线长648 m，根据式（6）计算大坝基本自振周期1.0 s考虑三维河谷影响修正为1.4 s；依据坝址地震危险性分析报告，场地特征周期为0.41 s，加速度峰值为0.205 g，查图6得到滑块最大加速度反应放大倍数为4.2，即amax为0.85 g；根据筑坝材料的强度，由式（7）计算屈服加速度ay为0.28 g；利用公式（8）求得坝顶竖直方向永久位移为：V平均＝0.12 m； V上限＝0.46 m；V下限＝0.01 m。采用公式（9）求得坝顶水平方向永久位移为：U平均＝0.08 m；U上限＝0.24 m；U下限＝0.01 m。

5 结论

大坝自振周期、场地地震卓越周期、潜在滑块屈服加速度与坝址基岩加速度峰值等对地震区土石坝的永久变形有明显影响，本文基于实际震害提出的土石坝永久变形计算公式，具有较好的精度。土石坝永久变形的计算结果表明，强震区采用现代重型振动碾压方法建造的密实堆石坝，震后永久变形较小。

[1]顾淦臣.土石坝地震工程［M］.南京：河海大学出版社，1989.

[2]SINGH R，ROY D，JAIN S K.Analysis of earth dams affected by the 2001 Bhuj Earthquake［J］.Eng.Geol.2001，80：282-291.

[3]NAGAYAMA I，YAMAGUCHI Y，SASAKI T，et al.Damage to dams due to three large earthquake occurred in 2003，in Japan［C］//36th Joint Meeting，Panel on Wind&Seismic ，Effects US-Japan Natural Resources Devel⁃opment Program，Japan.2004.

[4]SEED H B，LEE L，IDRISS I.Analysis of the slides in the San fernando dam during the earthquake of February 9，1971［R］.Report，Uni.Of California，Berkeley，1973.

[5]NEWMARK N M.Effects of Earthquake on Dams and Embankments［C］//Fifth Ranknie Lecture，Geotechnique，1965，15：139-160.

[6]MAKDISI F I，SEED H B.Simpfilied procedure for estimating dam and embankment earthquake-induced defor⁃mation［J］.J.Geotech.Eng.，1978，104：849-867.

[7]SARMA S K.Seismic stability of earth dams and embankments［J］.Geotechnique，1975，25（4）：743-761.

[8]LING H I，et al.Soil slopes under combined horizontal and vertical seismic accelerations［J］.J.Earthquake Eng and Structure Dyn.，1997，26（12）：1231-1241.

[9]JINMAN K，NICHOLAS SITAR M.Direct estimation of yield acceleration in slope stability analyses［J］.Journal of Geotechnical Geoenvironmental Engineering，2004，130（1）：111-115.

［10]YEGIAN M K，MARCIANO E A，GHAHRAMAN V G.Earthquake-induced permanent deformations：Probabi⁃listic approach［J］.J.Geotech.Eng.1991，117：35-50.

［11]SERFF N，SEED H B，MARKDISI F I，et al.Earth-quake induced deformation of earth dams［R］.Report No.EERC 76-4，University of California，Berkeley，1976.

［12]KRINITZSKY E L，HYNES M E.The Bhuj，India，earthquake：lessons learned for earthquake safety of dams on alluvium［J］.Eng.Geol.2002，66 ：163-196.

［13]HARDER Jr L H.Performance of earth dams during Loma Prieta earthquake［C］//Proc.，2nd Int.Conf.on Re⁃cent Advances in Geotechnical Earthquake Engrg.，1991，2：1613-1629.

［14]OZKAN M Y，OZYAZICIOGLU M，AKSAR U D.An evaluation of Güldürcek dam response during 6 June 2000 Orta earthquake［J］.Soil Dyn.Earthqu.Eng.2006，26：405-419.

［15]YASUDA N，KONDO M，SANO T，et al.Tomita，M.，Effect of the mid Niigata prefecture earthquake in 2004 on dams［C］//37th Joint Meeting，Panel on Wind&Seismic Effects，US Japan Natural Resources Development Program，Tech.Rep.，2005：1-16.

［16]BUREAU G，VOLPE R L，ROTH W H，et al.Seismic analysis of concrete face Rockfill dams［C］//Concrete Face Rockfill Dams-Design，Construction and Performance.ASCE，1985：479-508.

［17]ARRAU L，IBARRA I，NOGUERA G.Performance of Cogoti dam under seismic loading［C］//IConcrete Face Rockfill Dams-Design，Construction and Performance.ASCE，1985，1-14.

［18]RESENDIZ D，ROMO M P，MORENO E.El Infiernillo and La Villita dams：Seismic behavior［J］.J.Geotech.Eng.1982，108：109-131.

［19]ELGAMAL A W，SCOTT RF，SUCCARIEH MF.La Villita dam response during five earthquakes including per⁃manent deformation［J］.J.Geotech.Eng.1990，114：1443-1462.

［20］PENDER M J，ROBERTSON T W.Edgecumbe earthquake：reconnaissance report［Z］.Earthquake Spectra，EE⁃RI，1987：659-745.

［21]BOULANGER R W，BRAY J D，MERRY S M.Three dimensional dynamic response analysis of Cogswell Dam［J］.Can.Geotech.J.1995，32：452-464.

［22]OZKAN M Y，ERDIKM，TUNCER MA.An evaluation of Surgu dam response during 5 May 1986 earthquake［J］.Soil Dyn.Earthqu.Eng.1996，15：1-10.

［23]陈生水，霍家平，章为民.5.12汶川地震对紫坪铺混凝土面板坝的影响及原因分析［J］.岩土工程学报，2008，30（6）：796-801.

［24]王复来，郭俊仃.碧口土石坝与混凝土防渗墙在各运用期的应力与位移的分析［J］.岩土工程学报，1984，6（6）：1-17.

［25]SEED H B，IDRISS I M，KIEFER F W.Characteristics of rock motion during earthquakes［J］.J.Soil.Mech.Found.Div.ASCE，1969，95（SM5）：1199-1218.

［26]冈本舜三．耐震工学［M］.オ一ム社，1971．

［27]陈明致，金来鋆.堆石坝设计［M］.北京：水利出版社，1982．

［28]李俊杰，韩国城，林皋.混凝土面板堆石坝自振周期简化公式［J］.振动工程学报，1995，8（3）：274-280.

［29]ABDELGHAFFAR A M.Analysis of earth dam response to earthquakes［J］.J.Geotech.eng.，1979，105：1379-1404.

［30]NOSE M.Results of earthquake observations and dynamic test on rockfill dams and their consideration［C］//Proc.12th ICOLD.Mexico，1976：919-934.

［31]METE Oner.Estimation of the fundamental period of large earthfill and rockfill dams［J］.Soils and Foundations，1984，24：1-10.

［32]ABDELGHAFFAR A M，SCOTT R F.Dynamic properties of earth dams［C］//Proc.7th World Conference on Earthquake Engineering，Istanbul，1980.

［33]KEIGHTLEY W.A dynamic investigation of Bouquet Canyon dam［Z］.EERL，California Institute of Technolo⁃gy.1964.

［34]ATRAKOVA T S.A study of dynamics of earth dams during earthquakes［C］//Proc.5th World Conference on Earthquake Engineering，Roma，1973.

［35]ONER M，ERIDIK M.Dynamic properties of embankment dams［C］//Proc.Int.conf.on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics，St.Louis，1981.

［36]OKAMOTO S.Introduction to Earthquake Engineering［M］.University of Tokyo Press，1973.

［37]HELLER L W，AHLBERG J E.Earth dam motion due to a deep nuclear explosion［C］//Proc.5th World Confer⁃ence on Earthquake Engineering，Roma，1973.

［38]ABDEL-GHAFFAR A M，SCOTT R F.Experimental investigation of the dynamic response characteristics of an earth dam［C］//Proc.2nd US National Conference in Earthquake Engineering，1979.

［39]韩国城，孔宪京，王炳乾，等.关门山面板堆石坝现场弹性波试验研究［J］.大连理工大学学报，1990，30（5）：560-568.

［40]NB 35047-2015水工建筑物抗震设计规范［S］.北京：中国水利水电出版社，2000.

［41]SINGH R.A correlation for permanent earthquake-induced deformation of earth embankments［Z］.Eng.Geolo⁃gy，2007：174-185.