基于盲分离的多分量LPI雷达信号检测

郭 薇,廖林炜,张柏林

(1.海军驻武汉438厂军事代表室,湖北 武汉 430064;2.海军驻中南地区光电系统军事代表室,湖北 武汉 430233;3.94810部队,江苏 南京 211500)

基于盲分离的多分量LPI雷达信号检测

郭 薇1,廖林炜2,张柏林3

(1.海军驻武汉438厂军事代表室,湖北 武汉 430064;2.海军驻中南地区光电系统军事代表室,湖北 武汉 430233;3.94810部队,江苏 南京 211500)

针对现有信号处理模型难以解决多分量信号的处理问题,以及现有的多分量处理只讨论了多分量LFM信号的问题，提出了一种新的多分量处理模型和处理方法,首先通过改进的FastICA盲分离算法实现多分量信号的分离,提出了一种基于AHT的判别方法,对分离后的噪声和信号进行判别,有效地解决了多分量信号的检测处理难题。

独立分量;盲分离;多分量;信号检测

低截获概率雷达(LPI雷达)的大量装备使战场电磁环境更趋复杂。LPI雷达信号与常规雷达信号并存,要求电子侦察设备兼具这两种雷达信号的处理能力。由于LPI雷达信号具有大的时宽带宽,在实际的侦测环境中LPI信号与常规信号常常会在时频域出现混叠形成多分量信号,而常规信号的功率值要远远大于LPI信号,使对LPI信号的检测处理变得异常困难,对于LPI雷达信号的检测问题的研究仅仅局限于噪声信号环境下来进行已经远远不能满足实际需求[1-3]。

1 多分量信号模型的建立

由于事先难以确定混合信号中所包含的各信号的类型,因此利用传统信号处理方法难以对多分量信号进行有效处理。为了更好地理解多分量处理算法,本文对独立分量法(ICA)[4]进行阐述。假定混合信号中的各分量间相互独立,在接收时发生了混叠。利用ICA法进行分量分离的思想是[5-6]:当多个接收传感器同步观测到混合信号时,针对观测到的混合信号通过解混的方式来完成分量的分离，ICA法的处理模型如图1所示。

图1 基于ICA的多分量信号盲分离处理模型

信号盲分离处理算法主要可分为:基于二阶统计量法和基于高阶统计量法。盲分离实质是一种求取最优解的过程,即使得分离出的各分量间尽量独立且与原信号最接近。

信号混合模型可表示为[7]:

(1)

其对应的矩阵表示形式为:

x=As+n

(2)

在式(2)中设相互独立的辐射源信号数目为n,其信号序列为s=(s1,s2,s3,…,sn),观测信号的数目为m,观测信号序列为x=(x1,x2,x3,…,xm)。矩阵Am×n表示混合矩阵,代表了分量间的混合系数,并且假定Am×n为列满秩,n表示均值为零的高斯白噪声。

为了保证输出信号最独立,利用ICA模型进行处理时必须满足[8]:

1)各个信号源之间必须满足相互统计独立。

2)混合信号最多只能有一个高斯分量。

3)m≥n，即观测到的混合信号数目应不小于源信号的数目。

当在ICA分析模型中满足以上约束条件时,即可保证分离出各分量。

由文献[8]可知,当辐射源数目n和观测信号m满足n≤m时,可以求得矩阵W,利用W可以使这m路观测信号通过线性变换得到估计的各分量信号y,并且得到的各分量与原信号最接近,其分离过程可表示为

y=WHx

(3)

2 现有FastICA盲分离处理算法分析

由于侦察截获接收机在实际侦察截获处理过程时没有任何先验知识可以利用,因此在对信号进行分离处理前需要对信号进行预处理来降低后续处理的难度,FastICA进行盲分离处理主要分为两步:1)对各传感器的观测信号作中心化和白化处理;2)提取独立分量,完成各分量的提取。其对应的处理流程如图2所示。

图2 基于FastICA算法的盲分离处理流程图

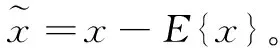
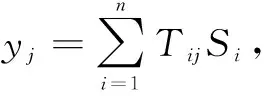
FastICA算法中最为重要的一步是对非高斯性的衡量,确定其最大值。目前非高斯性的度量方法主要有基于峭度和基于负熵最大等方法。下面将详细介绍这两种方法。

定义一个随机变量x的峭度为[9]

kurt(x)=E(x4)-3E(x2)2

(4)

如果观测信号的概率密度分布趋近于高斯分布时,其对应的峭度值将比其中的任一分量信号更接近于0,通过调节分离矩阵W,当观测信号的峭度值最大时,那么此时输出y为对辐射源各信号的最优估计。

定义随机变量x的负熵为[10]:

J(x)=[E{G(x)}-E{G(xgauss)}]2

(5)

式中xgauss是方差与x相等的高斯变量,G(x)为非线性函数。由式(5)可知当x为高斯变量时,则对应的负熵也为0,其负熵随着x的概率密度函数远离高斯分布而增大。因此只要使y的负熵最大即可求得W。

虽然用峭度来衡量非高斯性较为简单,但峭度对野值比较敏感,容易造成较大偏差,因此多采取负熵作为衡量非高斯性的工具。设分离矩阵W的第i个行向量为wi(i=1,2,…,n)，yi为第i个分离信号。

为了得到分离矩阵在此引入一种定点迭代方法:

(6)

式中，v为经过白化处理的观测数据,g为非线性函数G的导函数,本文采用的非线性函数为g(x)=log(a2+x)，在式(6)两侧同时加上αwi则有

(7)

式中，α可由牛顿迭代法求得。根据非线性规划中Kuhn-Tucke最优化条件,当满足E{(wTv)2}=‖w‖2=1时,E{G(wTv)}的最优值为

E{vg(wTv)}-βw=0

(8)

其中β为常量。采取牛顿迭代法进行求解可得

(9)

(10)

利用FastICA进行独立分量的提取的具体步骤如下:

Step1:初始化分离向量wi,初始值为随机选择。

Step2:以负熵J(y)为目标函数,选取式(10)作迭代处理,得到分离向量。

Step3:当迭代求取第i+1个分离向量时,每迭代一次需要对前i个分离向量进行正交化投影并且进行归一化,正交投影方法采用Gram-Schmidt正交方法,做正交投影的目的是去除向量间的相关性。正交化过程如下:

(11)

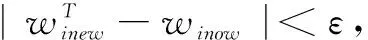
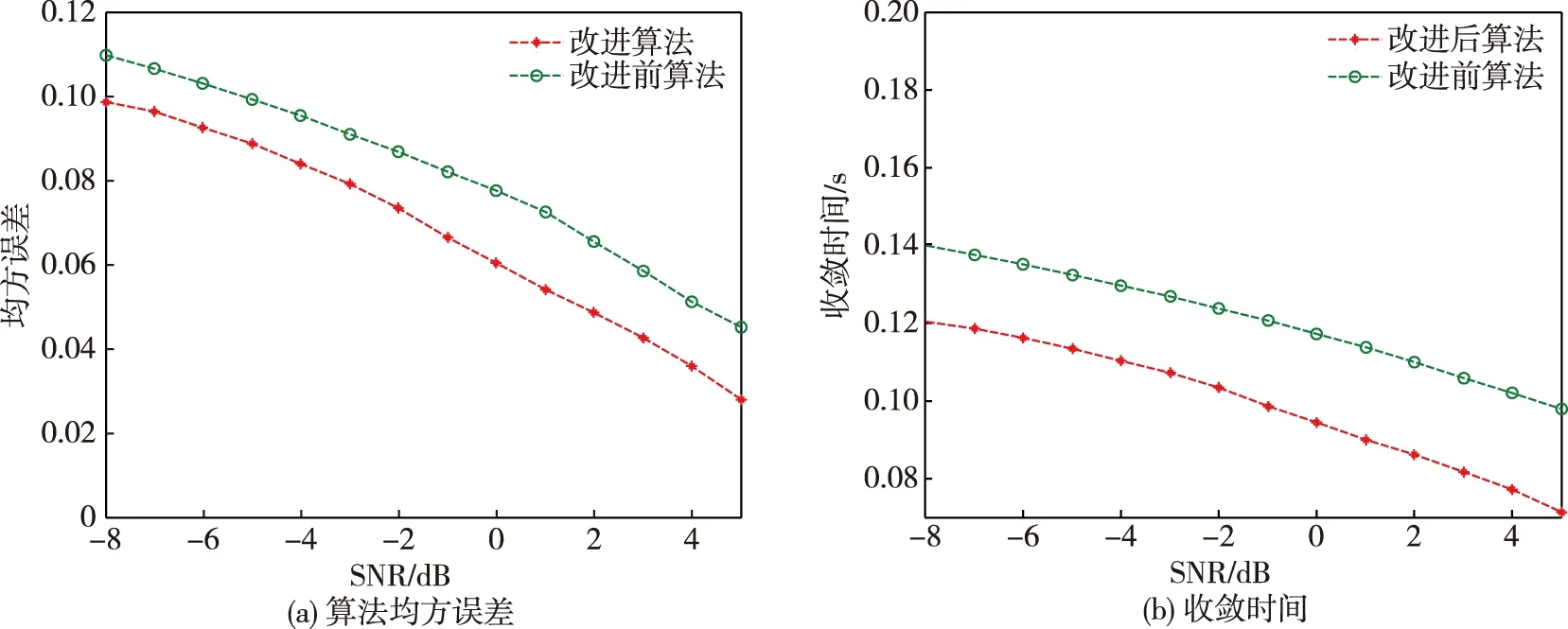
Step5:若i

该处理方法利用正交化得到相互正交的分离向量,从而保证得到不同的分离信号,但是当含噪ICA处理算法分离得到的前i个分离向量存在误差时,在求取第i+1个向量时,误差会得到积累从而使后续分离向量误差增大,进而影响信号分离提取效果。

3 改进的FastICA盲分离处理算法

上述所分析的FastICA盲分离处理算法被称为串行FastICA算法,其所采用的正交化方法为Gam-Schmit正交化方法,分离向量的误差会在后续的正交化过程中进一步累积,从而影响独立分量的提取效果。对称正交化FastICA针对FastICA正交过程中的误差积累问题,通过改进正交化方法,实现了分离向量的并行估计。在对称正交化FastICA中,分离向量wi不是一个一个估计出来的,而是同时估计出来的。

对称正交化方法由古典的矩阵平方根方法实现:

(WWT)-1/2W→W

(12)

式中,对称矩阵WWT经特征值分解方法得

WWT=Pdiag(d1,d2,…,dn)PT

(13)

所以(WWT)-1/2可以由下式求得

(14)

利用对称正交化方法可以消除Gam-Schmit法的误差积累影响,并且确保了每次分离出的信号分量不同,为了进一步改善算法性能提高算法的收敛速度,引入五阶牛顿迭代法来进一步优化算法。

传统的FastICA算法在对分离向量进行更新时多采用二阶牛顿迭代算法,其对应的迭代公式为

xn+1=xn-[f(xn)/f′(xn)]

(15)

迭代公式(9)由式(15)推导求得,为了加快算法的收敛速度，现对二阶牛顿迭代法进行改进,得到迭代公式:

(16)

式(16)为五阶收敛,因此可得五阶收敛的牛顿迭代公式:

(17)

至此可以得到改进后的FastICA的迭代公式如下:

(18)

利用五阶牛顿迭代法来代替传统算法中的牛顿迭代法可以大幅度减少迭代次数,提高算法收敛速度,提高算法的实时性。下面给出改进后FastICA算法的具体步骤:

Step1:对分离矩阵W={w1,w2,…,wn}进行初始化,初始值为随机选择,且满足‖wp‖=1,p=1,2,…,n。

Step2:令i=1,以负熵J(y)为目标函数,利用式(18)进行五级迭代处理,得到分离向量。

Step3:每次迭代后需要对分离向量进行正交化和归一化,正交过程采用对称正交化方法。正交化过程如下:

(19)

Step5:若i

4 信号与噪声的判别方法

截获到的多分量雷达信号地经过FastICA盲分离处理后,各个信号分量被分离提取出来,但是输出信号的顺序排列具有不确定性。为了顺利地对输出信号进行检测、识别、参数估计等后续处理,需要确定哪路输出为信号,哪路输出为噪声。为此本文提出一种基于AHT的判别方法,下面将对其做详细的介绍。

AHT是通过利用信号的模糊函数的性质以及信号的周期性来实现信号检测的一种时频分析方法,在信号对应的调频斜率和信号周期内呈现冲激函数特征,因此AHT是一种十分有效的信号分析方法。AHT变换为m×n的矩阵A。基于AHT的零均值噪声抑制判别方法判别过程为:

Step2:更新矩阵A,更新规则为

Step3:选取门限fT及一个接近零的正数ε,判断aver是否大于ε,若大于则返回Step1;

Step4:若max{aij}>fT则该输出信号为信号,否则为噪声。

经过上述基于AHT的零均值噪声抑制判别方法的处理有两方面的优点:一是可以对经过FastICA盲分离处理得到的各路输出信号进行判断,保证后续信号处理的正确进行,为准确的情报处理奠定基础;二是可以进一步抑制噪声,使对信号的参数估计更加准确。

5 仿真实验及结果分析

为了验证所提模型及处理方法的有效性,现利用本文方法对多分量信号的分离检测进行仿真实验,并与传统的检测算法进行对比分析。

为了进一步验证算法具有普遍性采用3个信号分量进行检测试验,所采用信号依次为线性调频(LFM)信号、二相编码(BPSK)信号以及噪声信号,固定载频(NS)信号的归一化频率为0.2,LFM信号的起始频率为0.15,截止频率为0.35,Barker信号的归一化频率为0.25,码元长度为13,采样点数为512点,LFM信号对应的信噪比SNR=-5dB。利用本文方法进行仿真实验,通过盲分离处理可以提取到3个信号分量,如图3所示,其中横轴表示采样点。

图3 基于FastICA盲分离处理的多分量信号处理

对各信道输出进行噪声与信号的判别,本文判别方法效果如图4所示。

选择检测门限fT=0.3,由判别结果可知输出信道2为噪声,输出信道1、3、4为信号,并且经过判别处理后,信噪比得到进一步改善,有利于处理工作的进一步进行。

为了进一步验证算法的抗噪性能,取2个LFM信号分量,在信噪比为-8～5dB的信噪比范围内进行蒙特卡洛实验,信噪比间隔为1dB,采样点数为512点,参数设置为:分量1起始频率为0.1,截止频率为0.3;分量2起始频率为0.2,截止频率为0.35。得到仿真结果如图5所示。

由仿真结果可知本文处理算法在处理速度及分离效果方面均优于改进前的算法。通过仿真分析可知本文方法对于多个信号的检测处理效果优于传统的时频分析方法,并且在进行信号分离时不受信号类型和参数的影响。

6 结束语

针对LPI信号的截获处理过程中的多分量信号的处理难题,设计了一种新型多分量信号分离处理模型,提出了一种改进的FastICA盲分离算法及判别方法,首先利用FastICA盲分离算法完成多个信号分量的分离,然后通过基于AHT的判别方法对分离后的信号进行判别,最后通过仿真实验验证了方法的正确性和有效性,实验结果表明本文提出的多分量处理模型在进行处理时与被处理信号的波形无关,具有很好的适应性。

图4 本文判别算法处理结果

图5 蒙特卡罗实验结果

[1] 杨福生,洪波.独立分量分析的原理与应用：信号与信息处理丛书[M].北京:清华大学出版社,2006.

[2] Ito J, Roy S, Liu Y, et al. Whisker barrel cortex delta oscillations and gamma power in the awake mouse are linked to respiration[J]. Nat Commun, 2014(5)：3572.

[3] Wang J, Zhou J, Peng B. Weak signal detection method based on Duffing oscillator[J]. Kybernetes, 2009, 38(10):1662-1668.

[4] 王垒.基于独立分量分析盲源分离方法的研究[D].兰州:兰州大学,2010.

[5] 王建雄,张立民,钟兆根. 基于FastICA算法的盲源分离[J]. 计算机技术与发展,2011,21(12):93-96.

[6] 王永涓. 基于改进FastICA算法的地震信号去噪研究[D]. 成都：成都理工大学,2012.

[7] 宋祺,杨承志,孙鑫. 基于FastICA的雷达信号分选研究[J].现代电子技术,2010,33(15):29-32.

[8] 姚俊良,杨小牛,李建东,等. 一种消除误差累积的多级快速独立分量分析算法[J]. 电子与信息学报，2009,31(11):2643-2648.

[9] 高巧玲,刘辉. 一种峭度FastICA改进算法[J].计算机技术与发展，2010,20(11):114-116+121.

[10]杨家轩,贾传荧,史国友,等.基于负熵准则的FastICA盲多用户检测的研究[J].电子与信息学报，2009,31(9)：2274-2277.

Multi-component of LPI Radar Signal Detection Based on Blind Source Separation

GUO Wei1, LIAO Lin-wei2, ZHANG Bo-lin3

(1.Military Representative Office of Navy in Wuhan 438 Factory, Wuhan 430064;2.Photoelectric System Military Representative Office of Navy in mid-south area,Wuhan 430233;3.No.94810 Troops of PLA, Nanjing 211500, China)

There is a problem in existing multi-component treatment models and algorithms, and only the multi-component LFM signals are discussed. To solve above problems, this paper proposes a new processing model and processing method. Firstly multi-component signal separation is realized through the improved FastICA blind source separation algorithm and a discriminant method based on AHT is proposed. Therseparated noise and signal are discriminated, solving the knotty problem of the multi-component signal detection processing.

independent component; blind source separation; multi-component; signal detection

2016-11-03

郭 薇(1983-),女,山东穗州人，硕士,工程师,研究方向为模式识别与智能系统。 廖林炜(1984-),男,工程师。 张柏林(1990-),男,硕士,工程师。

1673-3819(2017)01-0089-05

TN957；E917

A

10.3969/j.issn.1673-3819.2017.01.019

修回日期： 2016-12-04