数学教学中“留白”的意义及运用

杨凯明

[摘 要] “留白”是一种教学思想，是一种教学智慧，更是一种追寻教学意境的艺术。教师要创造一个有利于学生主动发展的教学环境，给学生充分发展的空间与时间，把学习的主动权还给学生，体验成功的乐趣，培养学生的创新意识和创新能力。教师恰到好处的“留白”，有助于教师生动地“解惑、授业”，做到相机诱导，激发学生的学习兴趣，让学生在求知的过程中能主动地去探究、思考、发现，主体意识得以充分发挥。

[关键词] 留白艺术；思维；探究

追求“无为处皆成妙境”的一种空灵意境，通过无限遐想享受书画之美。其实，“留白”是一切艺术共有的表现手法，数学教学的“留白”亦有异曲同工之妙。课改初期许多教师大多追求课堂的“热闹”，认为那样的课堂才是灵动的。随着课改十多年的积淀，数学课堂须回归理性，追寻学生思维的发展，因而教学中“留白”至关重要。

一、教学“留白”的作用与意义

小学数学教学中的“留白”是教师在课堂教学中根据教学需要，不直接把一些学习内容明确告知学生，而是通过言语激发、提出问题等方式留下“空白”，让学生充分展开联想，开展讨论与交流，激发学生的求知欲。鼓励学生自主探究、动手实践、合作交流，利用自己的思维活动填补知识空白。

教学“留白”是一种教学策略。“留白”不是避而不谈、避重就轻，而是铺垫与蓄势，注重疏密调节，动静搭配。数学课堂教学中巧妙的“留白”能使学生拥有“完全投入数学活动的机会”，给学生在知识上、心理上的暂时性空白，留足能让学生自由思考的余地，留给学生思维驰骋的时间和空间，让学生完整经历一个学习数学的过程，从而提高数学教学效率。学生的思维活力也就是在教学“留白”中迸发出来的。

二、教学“留白”的方法策略

“留白”首先考验的是教师的教学预设功底，“布白”要从全局出发，精心设计。如何精于“留白的布局谋篇”，笔者认为可以从课堂的几个环节入手：

（一）导学“留白”，激发学生学习兴趣

导学是课堂中良好的开端，至关重要。导学的关键是吸引学生，激发兴趣。我们要依据教材内容和教材的特点，抓住学生好奇心强的心理，把“留白”巧妙地运用到导学中来，有意给教材的知識蒙上一层神秘面纱，让学生处于一种“心求通而未达，口欲言而未能”的状态，激起他们强烈的求知欲望，促使他们主动积极地参与到学习中来。当然，这里的“留白”需要把握好尺度，留得恰到好处，才能起到聚焦课堂的作用。留下认知冲突，使学生带着思考和疑问参与到课堂中，唤起学生的求知欲，激发学生的注意和思考。

如教学北师大版三年级《数学》下册“面积单位”一课时，笔者是这样预设“留白”的：

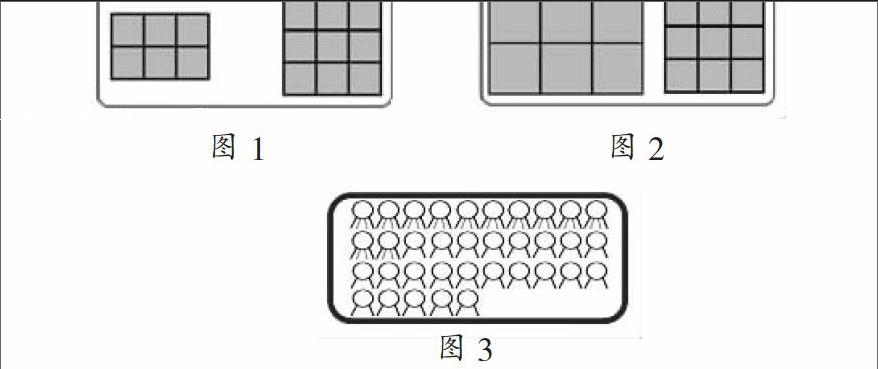
师：我们已经认识了面积，现在一个长方形由6个小正方形拼成，一个正方形由九个小正方形拼成。请同学们猜猜看这个长方形和这个正方形谁的面积大？

课件中出示图形，学生恍然大悟。接下去再学习“面积单位”，标准统一的必要性就不言而喻了。

学生有自己的思维习惯，许多时候是有思维定式的，如以上的教学中学生习惯性地认为9个小正方形肯定大于6个小正方形，忽略了小正方形大小标准是否统一，从起初的异口同声到一脸不解，再到恍然大悟，学生以“留白”获取到知识。导学的“留白”，主要通过设置疑问，造成学生思维上的认知冲突，给学生留有思维和知识上的“空白”，从而激起学生通过学习来填补“空白”的求知欲，更能激发学生的学习兴趣和探究热情。

（二）探究“留白”，提高学生思维能力

苏霍姆林斯基曾说过：“有经验的教师往往只是稍微打开一扇通向一望无际知识原野的窗子。”在新课改课堂教学中，特别是在“先学后教”的教学理念下，我们要有意识地把某些数学知识给学生，给予学生暂时性的知识空白，再以“问题串”的形式引导学生去探究。这种设计并不是对于部分知识的舍弃，而是从本质上去调动学生思维的主动性和积极性，去亲身探究、实践，然后获得数学知识和基本的活动经验。

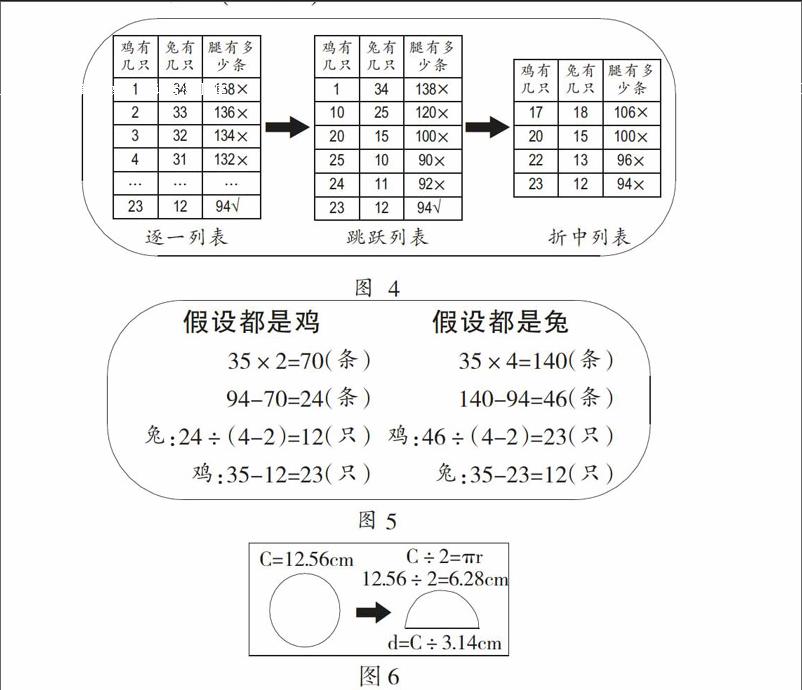
如教学“鸡兔同笼”时，解决鸡兔同笼的方法其实很多，各种版本的教材各自侧重点不同，综合考量、提问，给学生的思维很大“空白”。

教师出示“孙子算经”中的原题是：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？

师：读一读，你知道这道题的意思吗？你能解决这个问题吗？同学们先独立思考，然后小组交流。

教师出示合作学习要求：把自己的想法写在作业纸上，并在小组内介绍自己的方法。

小组长把不同的方法贴在合作学习单上，准备汇报。

假设都是鸡或都是兔，通过假设后腿的变化，来计算鸡和兔的只数。

教学中，教师只是做了简单的引导，其他都是学生在自己思考的基础上，通过小组交流的形式自主发现并解决问题。事实证明，这种上课效果明显提高。

（三）评价“留白”，拓展学生开放性思维

新课标中教师的角色定位是学生学习活动的组织者、引导者、参与者，而在实际的课堂教学中，教师往往最喜欢的角色还是导演。当学生按照自己设定的教案倾情演绎，学生的回答符合教师的意图或者按照教学设计的思路发展时，许多教师的态度是立即肯定，急于表扬。而这样的肯定和表扬是有漏洞的，会造成学生的求异思维、发散思维得不到培养。

在教学“圆的周长”时，圆的周长计算方法掌握不是很难，关键是理清半径、直径与圆周长之间的关系，计算也多是运用公式展开。可一到求半圆的周长时（如图6），问题就显现了。

[图6][C=12.56cm][C÷2=πr][12.56÷2=6.28cm][d=C÷3.14cm]

师：刚才我们计算出这个圆的周长是12.56厘米，现在我们把这个圆从中间切开，每个半圆的周长是多少厘米？

生：老师，6.28厘米！

师：同意的举手！（学生纷纷举手）

师：有没有不同意见？（有几个学生持不同意见）

生：老师我觉得应该是10.28厘米。

学生之间展开激烈的争论……

生1：圆的周长是12.56厘米，那么半圆的周长是圆周长的一半，12.56÷2=6.28厘米。

生2：不同意，你们的想法是错的。半圆的周长就是沿半圆走一圈，6.28厘米是这条曲线的长度，半圆还要加上这条直径的长度。

在这里，教师只是抛给学生一个问题，对个别学生的回答暂时不做评价，便引来了学生之间激烈的争辩。在这一过程中，学生不但找到了半圆周长的计算方法，更重要的是经历了计算方法的构建过程，并从中体验到了成功的乐趣。

（四） 总结“留白”，激发学生探索兴趣

好的导入加上精彩的结尾，是一堂好课的标志。课堂小结是一堂课走向成功的最后一步。要使结尾有深度、有效果，教师可以在课的结尾设置“留白”，让学生回顾和升华前面所学的知识，进一步激发学生探究的兴趣，能取得意想不到的教学效果。在一节课结束的时候，教师可提出一个或几个与本课教学内容相关的问题，让学生带着疑问结束一节课的学习，以“不全”求“全”，在有限中追求无限，可以增强学生主动探求新知的好奇心以及参与的意识，达到“言已尽而意无穷”的效果。

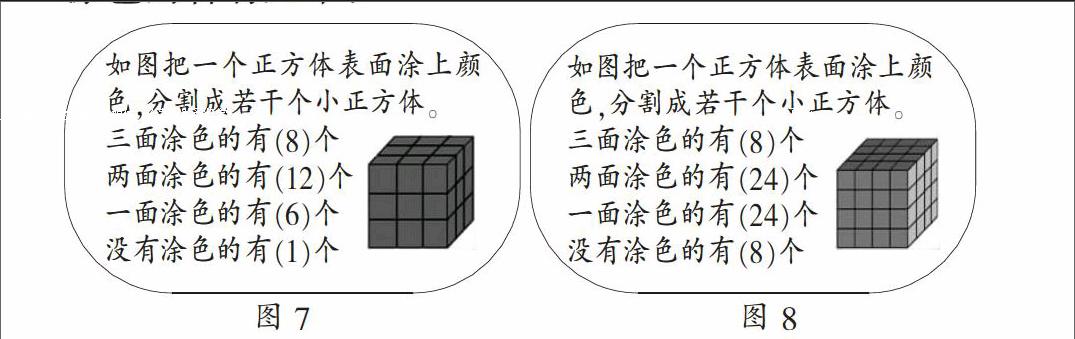
例如，教学列出如图7三阶魔方、圖8四阶魔方所示，提出问题：把一个正方形表面涂上颜色，分割成若干个小正方体，三面涂色、两面涂色、一面涂色和没有涂色的各有几个？

在解决三阶魔方和四阶魔方的问题后，课的结尾教师追问：“如果出现六阶魔方、十阶魔方呢，你能快速写出来吗？是不是有规律呢？”（接着要求课后写一则数学日记。）

以上片断看似在提问题，其实是教师通过对两个问题的对比，已经将解决问题的方法暗示给学生，让学生很自然地想到课后可以从正方体的顶点、棱、面和体积四个方面去探究，这些方法就使学生的探究过程有了手段保障；而“写一则数学日记”则保证了探究的结果。显然，这样的结束可谓言已尽而意无穷，把更广阔的思维空间留给课外。这样的收尾，能让我们感受到：虽然课已结束，而学生的思维活动却不停止，使整堂课显得余味无穷。

（五）练习“留白”，提升学生思维深度

练习“留白”的创设，学生积极性能够得到充分调动，避免了练习作业的单调和枯燥。除了对已学知识的一个固化，同时更能挖掘学生深层次的思维，充分体现“人人学习有价值的数学，人人都能获得必需的数学，不同的人在数学上有不同的发展”的本真思想。除了能够让学生在解题的过程中掌握知识要点，更能使学生个性彰显出来。

题2：圆的周长是20厘米，如果圆的面积和长方形的面积相等，计算图中涂色部分的周长是多少？

学生练习时发现，周长为20厘米，无法求出半径，按原来的方法无法计算，怎么办？此路不通另寻他路，这其实就是一个思维的提升。通过移动组合，学生发现阴影部分的周长就是（+圆周长）。

在教学时对“留白”的运用中，许多教师只把它当成了教学手段，有的过于夸大其作用而滥用。在教学活动中其表现诸如：有的为了追求探讨的形式，探究的问题没有价值；有的流于形式，一味放手，对学生的思维能力培养帮助不大；有的图花哨，不顾实效。这些做法都是片面的。“留白”要在达到所需效果的前提下和明确目标的基础上展开， “留白”应该是一种教学思想。应根据教学的需要灵活运用，不能为追求“留白”的形式而“留白”。只有所留之“白”能引起学生的数学思考，生出“实”来，才可以启发学生思维的教学“留白”。

责任编辑 满令怡