消费信贷市场均衡及其影响研究：一个无限生命跨期消费模型

李 杨 臧旭恒



消费信贷市场均衡及其影响研究：一个无限生命跨期消费模型

李 杨 臧旭恒

在非平稳收入过程、与收入相关的消费信贷上限假设下，通过加总微观跨期消费模型，考察消费信贷市场均衡。结果表明：消费信贷市场的潜在总需求大于总供给，市场均衡取决于总供给。消费信贷总供给的扩张存在规模边界。消费信贷同居民可支配收入之比是判断消费信贷总供给状态的重要依据。比例上升，消费信贷市场的总供给存在扩张空间。比例稳定，消费信贷总供给已经达到规模边界，总供给与消费信贷需求以及消费信贷市场风险相适应。规模边界下，短期刺激消费信贷供给的措施会使得高违约风险消费者获得消费贷款，增加市场违约风险。

消费信贷市场； 供给决定均衡； 消费信贷与收入之比； 规模边界； 跨期消费模型

一、引言

我国消费信贷①目前世界大部分国家对于消费信贷并不存在明确的定义，本文采用美国联邦储备委员会对于消费信贷的范围划定，即用于个人和家庭用于购买商品与服务的消费信用(不包含房产)，这一范围与中国国家统计局的消费信贷统计口径的主要差别在于不包含住房按揭贷款。本文出现的消费信贷数据都按照美联储划定的范围进行调整。业务始于20世纪90年代中前期。1999年2月中国人民银行发布《关于开展个人消费信贷的指导意见》，标志着中国的消费信贷业务正式开展，同时揭开了我国消费信贷市场迅速发展的帷幕。从微观上看，消费信贷市场的建立与发展是耐用品消费和消费品质升级的必然要求。消费信贷业务的开展有利于居民平滑一生消费，通过缓解流动性约束释放潜在的消费需求，扩大居民消费规模。从宏观上看，消费信贷是稳定消费需求的重要宏观调控工具。

美国的注资计划②定期资产支持证券贷款工具(TALF)计划。、我国的“家电下乡”、“以旧换新”等是通过消费信贷供给扩张达到刺激消费需求的效果，通过为潜在消费信贷需求创造供给来增加消费需求规模。这一政策选择有效性的隐性前提是存在消费信贷潜在需求和供给的缺口，并且这一缺口的表现形态是消费信贷总供给不足，然而存在这一隐性前提的理论依据是什么？

更进一步的，持续的扩大消费信贷供给，会使得原本因为违约风险过高无法获得消费贷款的消费者获得消费信贷，增加违约风险。市场违约风险的积累是影响针对消费信贷市场刺激措施可持续性的重要因素。但是市场中某些时期供给的持续增加并未显著增加市场风险。消费信贷市场为何会出现这样相互矛盾的状况？

的宏观环境和运行机制提供理论指导，但是缺乏对一国范围内消费信贷市场均衡的分析，缺乏对消费信贷市场供求状况所表现出的特殊形态的理论描述。本文在分析消费信贷市场供给和需求及其加总的基础上，建立加总的跨期消费模型，通过数值模拟寻求消费信贷市场的均衡解。基于对数值模拟均衡结果的分析，为短期刺激消费信贷的措施选择提供理论解释，进一步地，提供判断消费信贷市场供给增长与市场风险积累关系的方法，并最终提出相应的政策建议。

二、消费信贷市场供给、潜在需求及均衡综述

从个体消费者或家庭的角度出发，跨期模型(1)描述了一个寿命为N，年龄为t的消费者的跨期消费行为。该消费者会分配生命各期的消费，使得各期消费效用在当前的折现之和期望最大化。然而由于消费者不可能拥有无限的财富，所以这种分配受到一些限制，即流动性约束。

(1)

(2)

At+1=(1+r)(Ar+Yt-Ct)

(3)

At+1=(1+r)(At-(1+r)dt-1+dt+Yt-Ct)

(4)

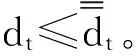
对个人或者家庭消费信贷需求的加总建立在人口年龄结构不变的假设上。加总过程实质上是用加权平均后的同质消费者替代原有的异质性消费者的过程，加总后将得到无限生命同质性消费者的跨期消费模型，这个模型代表众多同质消费者的集合，其收入、消费与消费信贷都是众多异质性消费者的加权平均值。这种加权平均的具体权重非常难获得，但是数学上这种加权平均一定存在，并且拥有一些确知的结论：

1.由于人口年龄结构不变，从而宏观上加总的结果体现为人口总数不变的无限寿命消费者集合。

加总后的跨期模型应该描述无限生命的消费者受到(4)式流动性约束的情形，具有下列形式：

(5)

At+1=(1+r)(At-(1+r)dt-1+dt+Yt-Ct)

(4)

(6)

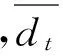
ξt=φξt-1+ut

(7)

0<φ<1,ut为白噪声

第二个环节是消费信贷的审批。王海侠*王海侠:《以博弈论分析我国消费信贷市场效率》，《金融研究》2000年第10期。及龙海明、黄卫*龙海明、黄卫:《消费信贷的供给与需求分析》，《消费经济》2005年第5期。等将消费者按照违约风险的不同划分为高风险消费者和低风险消费者，并赋予不同类型的消费者不同的违约概率。

供给上限的加总实质上是将申请者能够通过消费信贷审批的概率借助确定性等价原理融入到ω中的异质性消费者同质化过程。加总过程可以近似用(8)式描述：

(8)

其中，ki是加总时无法确知但一定存在的每一位消费者的权重。pi代表个体消费者成功通过消费信贷审批获得消费贷款的概率，i代表个体消费者，L代表总人口。

以总需求为基础的跨期模型加入总供给上限因素后变为如下形式：

(5)

At+1=(1+r)(At-(1+r)dt-1+dt+Yt-Ct)

(4)

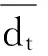
三、理论模型的建立与模型参数设定

基于(4)(5)式，建立处于t期，同质且无限寿命消费者的跨期消费模型：

(9)

s.t.Dt+1=(1+r)(Dt+Yt-Ct)

(10)

Dt=At-(1+r)dt-1

(11)

(12)

(13)

(14)

βi-t=1/(1+δ)i-t0<β≤1为未来第i期消费效用在t期的贴现。(12)式为横截条件。

Δyt=yt-yt-1=g+ηt-Ψηt-1g>0

(15)

定义的t期最高可能消费Xt

(16)

Xt即为t期所有可以用于消费的财富。由(14)式，t期消费的边际效用函数为

(17)

由(16)(17)及欧拉方程得到t期消费的边际效用

(18)

zt+1≡Yt+1/Yt=exp(g+ηt+1-ψηt)

(19)

记

(20)

(21)

进一步，代入(11)(13)(15)(16)式，有

(22)

(23)

模型中的未知函数p(·)由Simpsom法则近似得到。进一步的有：

(24)

对（24）式中的一些变量进行赋值*Ludvigson，s．，“Consumption and Credit：A Model of Time-Varying Liquidity Constrains”，The Review of Economics and Statistics，1999，81，pp．434447．：ψ＝0.44*Macurdy，T．E．，“The Use of Time Series Processes to Model the Error Structure of Earnings in Longitudinal Data Analysis”，Journal of Econometrics，1982，18，pp．83114*JS Pischke，“Individual Income，Incomplete Information and Aggregate Consumption”，Cheminform，1993，34（45），pp．64164．ｒ＝0.03 ｇ＝0.02 γ＝2 δ＝0.031／0.15设ξt，ηt为5维马氏链。其中，ηt为i.i.d，其5阶转移矩阵的每一个元素均为1/5，期望为0，方差记为0.02。进一步不再设定ξt具有随机性，这在进行模拟时不会出现问题，因为短期内ξt同模型中的其他变量间相对独立，长期看exp（ξt）的期望值为1。这一设定是为了消除没有预测到的宏观经济波动的影响，更容易观察消费信贷市场本身的演化。定义消费者寿命为150年，尽管这同无限寿命相矛盾，但对于80年的模拟时间跨度足够长。

四、数值模拟及结果分析

对(22)(24)数值模拟来求解居民采取最优消费策略时每一期的消费信贷均衡值、消费信贷供给上限和消费信贷潜在需求的关系。模拟中假定ξt与ωt不变，即消费信贷市场中没有任何干扰因素。1929年以前不存在消费信贷业务，从而供给和需求都处于市场出清状态，均衡值为0。消费信贷供给在1929年出现，市场供给上限由1929年以前的0突然增加到1/ωt·Yt,以此模拟在市场已经出清情况下突然增加供给后，市场均衡、消费信贷需求的变化。纵坐标为Xt/Ct=wt/θt。

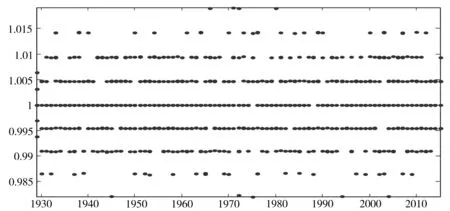
上图为ωt=4,δ=0.15的随机收入10样本模拟。消费信贷供给上限在1929年由0突然增加到1/ωt·Yt。由纵坐标可以看到，

(25)

数值模拟的结果表明：消费信贷市场均衡近似等于总供给上限，从而市场均衡由总供给决定。如果要在短期内刺激消费信贷市场，应当采取措施增加市场供给。此外，消费信贷市场的潜在总需求大于等于消费信贷供给上限，这说明消费信贷需求几乎不可能得到完全满足。然而消费信贷市场只有在产生并发展的早期呈现出卖方市场的特征。经过一段时期的发展后，反而没有明显的卖方市场特征。

更进一步的，增加供给刺激消费信贷规模的措施是否具有可持续性？一个基本的判断方法是考虑市场供给。如果市场供给本身就已经达到与市场风险相适应的水平：消费信贷供给规模边界，那么这些措施提高了消费信贷业务的收益水平，使得供给侧更加有利可图，这也就使得供给侧能够容忍更高的违约风险。但是持续的施行这些措施会导致市场风险的积累，这些风险很可能以爆发的方式释放。如果市场供给并没有达到规模边界，那么这些措施可以加快供给侧满足信用较好消费者消费贷款需求的过程，在不增加消费信贷市场风险的前提下扩大消费需求。

如果消费信贷供给并未达到规模边界，那么供给侧会因为利润的驱使自主地扩大供给；如果达到规模边界，供给侧会维持现有的供给规模。因此消费信贷市场本身供给规模的变化可以作为判断市场供给是否达到规模边界的标准。即：如果1/ωt维持稳定，说明市场供给已经达到规模边界，持续的刺激供给会累积市场风险。如果1/ωt上升，说明市场供给并未达到规模边界，持续的刺激有利于被压制消费需求的释放。

(26)

(27)

(27)式说明1/ωt可以由消费信贷与居民可支配收入之比近似计算。

五、结论与政策建议

本文对消费信贷市场的供给上限和潜在需求及其加总进行分析，建立无限生命跨期消费模型并进行理论推导与数值模拟，结论如下：

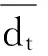
第二，1/ωt(消费信贷市场潜在供给能力中与居民收入无关的部分)的数值特征反映了消费信贷市场供给与市场风险的状态关系。1/ωt平稳意味着消费信贷市场供给已经达到规模边界，消费信贷业务的边际利润已经为0。这种规模边界与市场当前的违约风险相适应，这时持续的增加消费信贷市场供给容易积累市场风险。如果1/ωt持续上升，则说明消费信贷市场供给并未达到其规模边界，还有部分信用达标、违约风险较低的消费者没有获得消费信贷。1/ωt的值可以近似的由消费信贷与居民可支配收入之比dt/Yt计算。

根据研究结果，本文针对保障消费信贷市场健康发展、短期刺激消费信贷措施以及措施的可持续性提出政策建议：

由于消费信贷市场均衡由供给决定，短期刺激消费信贷规模应当采取增加供给的措施。如果消费信贷市场风险较高，那么采取措施降低市场风险或者降低交易摩擦带来的损失可以提高消费信贷供给规模。如果消费信贷市场的管理和信用体系比较完善，那么放松供给侧的流动性限制可以在短期刺激供给增长。

消费信贷供给侧刺激措施的可持续性取决于消费信贷与居民可支配收入之比dt/Yt。如果dt/Yt呈现上升趋势，说明需求侧一些信用较好、违约风险低的消费者还没有或者没有完全获得自己需要的消费贷款，供给侧扩大消费信贷业务依然有利可图。这时对消费信贷市场供给侧的刺激有利于扩大消费信贷规模，降低消费者的流动性约束，扩大消费规模。dt/Yt稳定表明消费信贷市场的供给已经达到规模边界，供给水平与市场风险相适应。当消费信贷市场总供给已达到规模边界时，短期刺激消费信贷供给的措施会使得原本因为信用问题无法得到消费信贷的消费者获得贷款，增加市场违约风险。这种情况下持续的刺激消费信贷供给会累积违约风险，带来严重市场隐患。如果在这种情况下依然需要刺激消费信贷市场，那么应该密切关注市场风险的积累，适当增加不良贷款拨备。

[责任编辑：贾乐耀]

Analysis on the Equilibrium of Consumer Credit Market and Influence——An Intertemporal-Comsumption Model of Unlimited Life

LI Yang ZANG Xu-heng

(School of Economics, Shandong University, Jinan 250100, P.R.China)

Supposing that income changes over time, and the upper-limit of consumer credit market depends on income, when we bring in Micro- Intertemporal-Consumption Model, we can find that the potential demand outweighs the aggregate supply, and the equilibrium depends on aggregate supply. There are scale boundaries to the expansion of aggregate supply. The ratio of consumer credit to disposable income is one of the important bases to measure the aggregate supply of consumer credit market. When the ratio increases, the aggregate supply expands. When the ratio keeps stable, which means the aggregate supply reaches to the scale boundary，the aggregate supply fits to the aggregate demand and market risk. Under the scale boundary, short-term measures to stimulate the consumer credit supply will bring consumer loans to people with high default risk, and increase the whole market default risk.

Consumer credit market; Equilibrium determined by supply; Ratio of consumer credit to disposable income; Scale boundary; Intertemporal consumption model

教育部哲学社会科学研究重大攻关项目“建立扩大消费需求的长效机制研究”(11ZD0016)。

李杨，山东大学经济学院博士研究生(济南250100)；臧旭恒，山东大学经济学院教授，博士生导师(济南250100)。