组合预测方法在重庆市GDP预测中的应用*

薛 倩, 牟凤云, 涂植凤

(重庆交通大学 建筑与城市规划学院，重庆 400074)

组合预测方法在重庆市GDP预测中的应用*

薛 倩, 牟凤云**, 涂植凤

(重庆交通大学 建筑与城市规划学院，重庆 400074)

GDP是国民经济发展的一个重要衡量标准，对其进行准确地预测非常重要；以重庆市为研究对象,基于统计数据，应用时间序列分析中的指数平滑法和ARIMA模型以及组合预测模型分别对2015—2020年重庆市的GDP进行了预测，并进行对比分析；研究结果表明：3种方法的误差均较小，但组合模型预测精度更高，重庆市未来几年的GDP年增长率将维持在10%左右。

指数平滑法；ARIMA模型；组合预测模型;重庆市；GDP

时间序列预测模型是指通过数据本身的序列研究来对其未来的变化作出分析和预测的方法[1-2]。首先采用时间序列中的指数平滑法和ARIMA(自回归求和滑动平均)模型分别对重庆市1997—2013年的GDP进行分析，并利用2014年的数据进行单一模型精度检验，再应用组合模型预测，并利用2005—2014年的数据对3种模型精确度进行对比分析，最终利用最优模型对2015—2020年的GDP进行预测。

1 研究区概况

重庆市的区位条件优势明显，位于长江经济带和海上丝绸之路的交汇处。目前，已经打通了渝新欧国际铁路贸易大通道，是我国多个对外开放口岸之一。并且与新加坡政府之间的合作使得重庆市在2015年成为中国与外国第三个政府合作的城市。这一切促使重庆经济发展问题成为人们的关注热点。

2 研究方法

通常对于GDP的预测方法主要有回归模型法、指数平滑法、灰色模型GM(1,1)法等，不同的方法具有不同的适用范围和特点。其中，回归分析法指利用数量统计的方法，利用现有的数据分析其变化规律并建立模型[3]。利用灰色预测模型进行预测时，对原始数据的要求较少，用于短期预测时精度较高，并且对模型的检验也比较容易，缺点是当数据分散程度较大时，其精度也会变差，因而不适合长期的预测[4]。经过模型比较，在单一模型选择时，选取GDP预测中应用最为广泛，且模型拟合程度较好的指数平滑法和ARIMA模型来对重庆市的GDP进行预测。

组合预测方法(综合预测、结合预测或复合预测)，是把不同单一预测进行组合，目的主要是希望能够更多地把各种方法所提供的信息综合利用，从而提高预测结果的精度[5]。组合预测方法在对GDP进行预测时，考虑了多种预测模型，使得在预测过程中由于考虑不全面而引起的误差变小，预测精度变高。

2.1 指数平滑法

指数平滑法是应用特殊的加权平均法对数据进行计算。采用指数平滑法进行预测，不必定量研究复杂系统的内部因素及其相互联系，而是仅从时间序列这个综合灰变量本身去寻找有用信息[6]，其主要原理是依据时间顺序对数据定义有区别的权重[7-10]。

2.2 ARIMA模型

ARIMA(Auto Regressive Integrated Moving Average)即自回归求和滑动平均，其前身是ARMA模型。ARIMA模型分为非季节性ARIMA模型和季节性ARIMA模型，即ARIMA(p，d，q)模型和ARIMA(p，d，q)(P，D，Q)模型，两者的区别在于季节性模型在进行预测时考虑了季节周期的因素，更加适用于有季节性或周期性变动的数据[11]。

研究数据是重庆市逐年的GDP数据，没有季节性变化，所以采用非季节性模型。其中AR和MA的阶数分别为p和q，差分的次数为d[12]。

由于ARMA模型及ARIMA模型都是在平稳时间序列基础上建立起来的，因此时间序列的平稳性是建模的重要前提，任何非平稳时间序列只要通过适当阶数的差分运算或者是对数差分运算就可以实现平稳[13]。

2.3 组合预测模型

组合模型预测方法是设一组观测序列{Xt}，t=1,2,…n，现在，分别用k个的模型对其进行分析并建模预测，每一个模型的预测值为Yti，则第t期的组合预测值可以表示为Yt=W1Yt1+W2Yt2，其中，Yti表示第i个模型在t期的预测值，Wi表示第模型在组合预测模型中的权重[5]。

在组合预测模型Yt=W1Yt1+W2Yt2中，其权重系数通常需要满足W1+W2=1。

在这里选择3种权重方法构建3种组合模型对GDP进行预测：

(1) 方差倒数法：

(1)

这种方法在实际应用中因其简单便捷，所以使用频率较高，其依据数据的误差平方和的大小对数据定义不同的权重，误差平方和越大，权重越小。

(2) 残差倒数法：

(2)

残差倒数法中Si的计算是Di的平方根，当数据差均为正值时两者使用无区别，但当数据差有正负区别时，两者使用有区别。

(3) 最小二乘法：

(3)

方法计算较为复杂，但克服了主观性强的问题，提高了预测的准确性和精确性，实际应用价值大。

确定好权重后，就可以根据Yt=W1Yt1+W2Yt2公式进行组合模型预测。

3 实例应用

3.1 数据准备

从《重庆统计年鉴》中统计出1997—2014年重庆市国内生产总值(表1)，并根据数据做出折线图(图1)，用以观察重庆市GDP的变化趋势。

表1 重庆市1997—2014年GDP值

图1 1997—2014年重庆市GDP值Fig.1 GDP from 1997 to 2014 in Chongqing

根据表1和图1可以看出重庆市1997—2014年GDP值序列是非线性变化，即不是平稳变化，且依据图1很明显，重庆市GDP在直辖之后呈现上升趋势，且2005年后上升趋势明显加快。

3.2 指数平滑法进行GDP预测

指数平滑分为一次、二次和三次，具体应用哪种指数平滑模型来对GDP值进行预测主要根据数据值的趋势和模型与实际值拟合的效果而定。

3.2.1 一次指数平滑

首先进行初值的选取，由于样本个数不多，所以预测初值选择为1997年的GDP值即X1=1 509.75。其次，依据公式，进行指数平滑前需要对其平滑系数进行选择，根据参考文献[15-17]，当时间序列中的样本数据呈现非平稳的趋势时，应选择较大的α值，即在0.6～1之间选择，所以选择α值为0.6,0.65,0.7,0.75,0.8,0.85,0.9,0.95分别对原始数据进行平滑预测(表2)，然后根据预测结果选择最合适的α值。

表2 不同α值时一次指数平滑预测结果

根据表2，可以看出，α取值越大，预测值与元数据拟合的程度越好。可以利用MSE(均方差)和MAD(绝对误差)对预测的数据拟合程度进行检验[17]。MSE、MAD的值越小则预测结果与真实值越接近。

根据表3，可以很明显地看出来，当α取值为0.95时MSE和MAD检验值最小，即与原始值最接近。即后面进行指数平滑时选择α=0.95来计算。

表3 MSE和MAD检验结果

3.2.2 高次指数平滑

根据指数平滑原理以及一次指数平滑的结果，对数据进行高次指数平滑运算。并以2014年数据为检测标准，对其进行预测及精度验证(表4、图2)。

表4 指数平滑计算结果

图2 一次、二次、三次指数平滑计算结果与元数据对比Fig.2 Once,twice,three times exponential smoothing results compared with metadata

根据表4和图2，可以很明显地看出，一次指数平滑在后期计算结果与源数据产生了较大的偏差，而二次、三次指数平滑结果均与源数据保持了较好的一致性。对比依据统计年鉴查得的重庆GDP数据(表4)，可以看出，三次指数平滑在增长速度上不如二次指数平滑的快，且二次指数平滑和原始数据符合程度更高，误差率仅为0.7%，所以选取二次指数平滑模型对2015—2020年的重庆市GDP值进行预测，得到表5。

表5 2015—2020年GDP值预测

3.3 ARIMA模型预测重庆市GDP值

应用ARIMA模型预测时，首先需要对序列进行平稳化处理。一般情况下，对于呈指数增长的时间序列，通常可以对其取对数，将其转化为线性趋势。在对序列取对数后，研究发现序列依旧是非平稳序列，所以还需要进一步平稳化处理，即对序列进行差分运算(图3)。根据图3可以看出，在序列进行一阶差分后，大部分数据还位于0以上区域，证明序列还未平稳，所以需要继续对其进行差分运算。二阶差分后可以看到数据也未完全达到平稳，进行三阶差分，可以看到，三阶差分后，所有数据基本都已达到平稳，皆在0附近，由此可以确定ARIMA(p,d,q)模型中的差分阶数d=3。

图3 一阶、二阶、三阶差分后结果(由左至右)Fig.3 First and second order and third order difference the results (from left to right)

当序列进行3阶差分后，序列已趋于平稳，所以可以定义剩余两个参数p和q。根据差分后生成的自相关图和偏相关(图4)，依据序列的拖尾性和趋势性进行参数p、q的取值，p=2，q=3，所以建立了ARIMA(2,3,3)模型，但是经过检验模型对实际数据拟合程度不够好，所以根据Spss 17.0改变参数设置，通过Spss 17.0中的自动建模模块以及对实际数据拟合精度的综合研究，最终建立ARIMA(1,3,3)模型。在Spss 17.0中进行检验，得到R2值为0.994，sig.均小于0.01，即证明这个模型通过检验，可以用其对2015—2020年的数据进行预测(表6)，同时以2014年数据比对统计年鉴查到的数据进行检验，误差率为3%，证明模型拟合程度较好。

图4 自相关系数图和偏相关系数图Fig.4 Autocorrelation coefficient and partial correlation coefficient

模 型2014201520162017201820192020GDP模型_1预测14693.0616762.7318786.4220715.3522407.0323751.2824625.87UCL16259.9820104.9724037.4828558.2433567.6339094.3744929.19LCL13249.9913882.7814500.3614706.4614446.6313672.3012454.61

3.4 组合模型预测重庆市GDP值

前面已经对重庆人均GDP分别建立了指数平滑模型和ARIMA模型，并且它们的预测效果都比较好。现在，结合前面的两种模型，在此基础上，根据3种权重系数的求取方法来建立3种组合预测模型：

利用方差倒数法，即公式1，来确定权重系数，并且通过公式Yt=W1Yt1+W2Yt2，对GDP进行预测，得到权重系数为W1(二次指数平滑)为0.48，W2(ARIMA模型)为0.52。即其预测模型为Yt=0.48Yt1+0.52Yt2。最终预测结果见表7。

利用残差倒数法，即公式2，来确定权重系数，并且通过公式Yt=W1Yt1+W2Yt2，对GDP进行预测，得到权重系数为W1(二次指数平滑)为0.9，W2(ARIMA模型)为0.1。即其预测模型为Yt=0.9Yt1+0.1Yt2。最终预测结果见表7。

利用方差倒数法，即公式3，来确定权重系数，并且通过公式Yt=W1Yt1+W2Yt2，对GDP进行预测，得到权重系数为W1(二次指数平滑)为0.5，W2(ARIMA模型)为0.5。即其预测模型为Yt=0.5Yt1+0.5Yt2。最终预测结果见表7。

4 总 结

根据指数平滑模型、ARIMA模型以及3种组合模型对GDP预测的值(表7)。

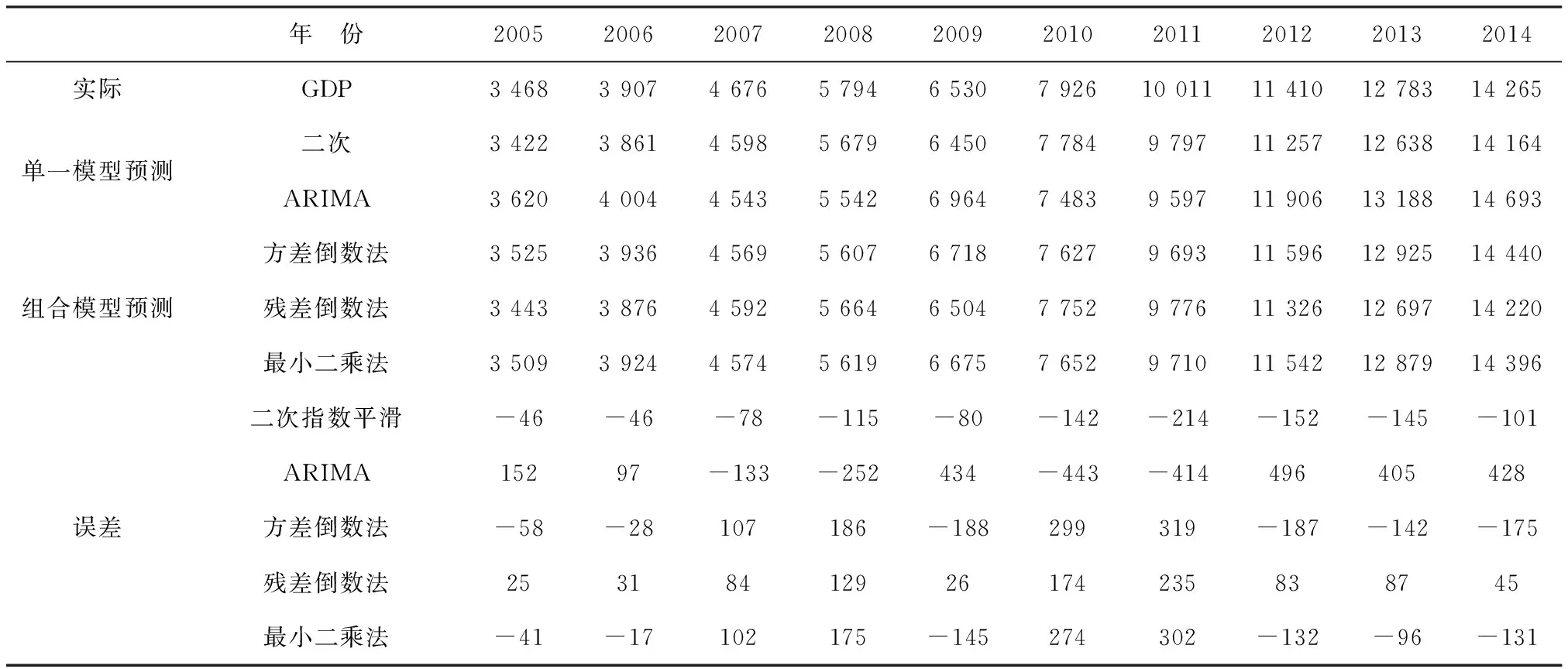
表7 各种模型误差检验

由表7可知，这5种预测方法精度都比较高，误差都较小。对比组合模型法和单一模型法在对GDP的预测，根据表7，组合模型中在预测精度上得到了很大的改进，尤其是当计算权重时选择残差倒数法，有效地减少了对GDP预测的误差，在实际应用中很好地降低了因理论计算预测时产生的误差而导致实际规划和决策中时间浪费现象产生的概率。所以将残差倒数组合模型法作为最优模型对2015—2020年的GDP进行预测(表8)。

表8 残差倒数法组合预测模型对重庆市2015—2020年GDP值预测

根据表8可以看出，重庆市未来6年经济持续性平稳增长，基本将以每年10%的增长率增长。重庆市2015年实际的GDP增长为11%，预测值接近，证明残差倒数法组合模型预测在针对重庆市GDP预测中具有一定的实用性。

研究结果表明:在对于GDP这种影响因素较多的实体，组合预测模型综合了单独模型各自的优点，使得预测结果更加接近真实值，具有更好的实用性。由于所构建的预测模型是基于GDP的时间序列数据，预测期并不太长，只选取了6年。若要对GDP进行较长期的预测，应结合考虑宏观经济因素，如何引入外部经济因素指标对模型进行改进是有待于进一步研究的课题。且对于组合模型的进一步研究以及单因子模型的选取都是值得研究的方向。

[1] 何新易.基于时间序列模型的中国GDP增长预测分析[J].财经理论与实践,2012,38(7):96-99

HE X Y.Analysis China’s GDP Growth Forecast Based on Time Series Model[J].Journal of Financial Theory and Practice,2012,38(7):96-99

[2] 李晴,杨春.时间序列分析模型及其在GDP预测中的应用研究[J].安徽农业科学,2011,39(2):12449-12451

LI Q,YANG C.Time Series Analysis Model and Application in the GDP Forecast Research[J].Journal of Anhui Agri-cultural Science,2011,39(20):12449-12451

[3] 张强,崔倩倩,马志辉.基于干预分析模型下的新疆GDP预测研究[J].重庆工商大学学报(自然科学版),2013,30(4):25-29

ZHANG Q,CUI Q Q,MA Z H.Xinjiang GDP Forecast Based on Intervention Analysis Model[J].Chongqing Technology and Business University(Natural Science Edition),2013,30(4):25-29

[4] 施泽军,李凯.基于灰色模型和指数平滑法的集装箱吞吐量预测[J].重庆交通大学学报(自然科学版),2008,27(2):302-304

SHI Z J,LI K.Forecast Container Throughput Based on Gray Model and Exponential Smoothing Method[J].Chongqing Jiaotong University (Natural Science Edition),2008,27(2):302-304

[5] 詹英.组合预测方法在我国人均GDP预测中的应用[D].武汉:华中师范大学,2014

ZHAN Y.Combination Forecasting Method in China’s Per Capita GDP Forecast[D].Wuhan:Central China Normal University,2014

[6] 芮海田,吴群琪,袁华智.基于指数平滑法和马尔科夫模型的公路客运量预测方法[J].交通运输工程学报,2013,13(4):87-93

RUI H T,WU Q Q,YUAN H Z.Highway Passenger Quantity Prediction Method Based on The Exponential Smoothing Method and Markov Model[J].Journal of Tran-sportation Engineering,2013,13(4):87-93

[7] 徐建新,严勇,严富海.指数平滑法在典型城市GDP预测中的应用[J].水利科技与经济,2008,14(7):551-554

XU J X,YAN Y,YAN F H.Application of Exponential Smoothing in Typical City GDP Forecast[J].Water Science Technology and Economy,2008,14(7):551-554

[8] 臧文亚.重庆港口吞吐量组合预测[D].成都:成都理工大学,2012

ZANG W Y.Chongqing Port Throughput Forecasting[D].Chengdu:Chengdu University of Technology,2012

[9] 刘薇.时间序列分析在吉林省GDP预测中的应用[D].长春市:东北师范大学,2008

LIU W.Time Series Analysis Application in The Jilin Prov-ince GDP Forecast[D].Changchun:The Northeast Normal University,2008

[10] 朱庆明,张浩.三次指数平滑法在煤矿事故预测中的应用研究[J].中国安全生产科学术,2012,8(4):103-106

ZHU Q M,ZHANG H.Three Exponential Smoothing Method Application in the Coal Mine Accident Prediction Research[J].Chinese Academic Production Safety,2012,8(4):103-106

[11] 吴敬婷.基于ARIMA模型的畜产品价格预测系统的研究[D].哈尔滨:东北农业大学,2012

WU J T.Livestock Prices Forecast System Based on ARIMA Model[D].Harbin: Northeast Agricultural Unive-rsity,2012

[12] 李辰飞,常婕,沈燕.ARIMA模型在湖北省GDP预测中的应用[J].湖北师范学院学报,2015,35(4):62-66

LI C F,CHANG J,SHEN Y.ARIMA Model in Forecasting the GDP of Hubei Province[J].Hubei Normal University,2015,35(4):62-66

[13] 龚国勇.ARIMA模型在深圳GDP预测中的应用[J].数学实践与识,2008,38(4):53-57

GONG G Y.ARIMA Model in Forecasting the GDP of Shenzhen[J].Mathematics Practice and Knowledge,2008,38(4):53-57

[14] 魏宁.时间序列分析方法研究及其在陕西省GDP预测中的应用[D].西安:西北农林科技大学,2010

WEI N.Time Series Analysis and Application in GDP Forecast in Shanxi Province[D].Xi’an:Northwest Agricu-lture and Forestry University,2010

[15] 王长江.指数平滑法中平滑系数的选择研究[J].中北大学学报,2006,26(6):558-561

WANG C J.Selection of Exponential Smoothing Method to Smoothing Coefficient[J].North University,2006,26 (6):558-561

[16] 吴小华.Excel在指数平滑法参数优选中的应用[J].安徽工业大学学报(社会科学版),2007,24(1):38 -39

WU X H.Excel Application of Exponential Smoothing Method to Parameter Optimization[J].Anhui University of Tech-nology (Social Science Edition),2007,24 (1):38-39

[17] 陈彦光.地理数学方法：基础和应用[M].北京:科学出版社,2010

CHEN Y G.Geography Mathematics: The Base and Appli-cation[M].Beijing:Science Press,2010

责任编辑：田 静

Application of Combination Forecast Method to Chongqing’s GDP Prediction

XUE Qian, MOU Feng-yun, TU Zhi-feng

(School of Architecture and Urban Planning, Chongqing Jiaotong University, Chongqing 400074, China)

GDP, as an important economic development measurement index, is important to be predicted. By using Chongqing as a study object, by exponential smoothing method in time series analysis, ARIMA Model and combination forecast model,Chongqing’s GDP during 2015—2020 is predicted and its comparative analysis is conducted. The research results show that the deviation of the three methods is small, however, the accuracy of combination forecast model is higher, and that Chongqing’s GDP yearly growth rate in the coming years will be maintained at about 10 percent.

exponential smoothing method; ARIMA Model; combination forecast model; Chongqing; GDP

10.16055/j.issn.1672-058X.2017.0001.012

2016-01-30；

2016-03-28.

重庆市前沿与应用基础研究计划项目(CSTC2014JCYJA00043).

薛倩(1993-)，女，新疆乌鲁木齐人，硕士研究生，从事国土资源与3S技术研究.

** 通讯作者：牟凤云(1979-)，女，山东高密人，博士，副教授，从事3S集成技术与应用和国土资源遥感研究.E-mail:76237408@qq.com.

T902

A

1672-058X(2017)01-0056-08