关于熵的可交换性

邹 成

(四川化工职业技术学院，四川 泸州 646005)

关于熵的可交换性

邹 成

(四川化工职业技术学院，四川 泸州 646005)

不管在测度空间还是拓扑空间上，两个连续映射复合后，其熵与复合的先后次序有关，但满足一定条件后，有些复合的顺序是可以交换的，即交换秩序后的熵保持不变.详细回顾了一些关于熵的定义，讨论了两个映射复合后其测度熵、测度序列熵、拓扑熵、拓扑序列熵、二维映射的拓扑熵、旋转熵及拓扑压的可交换性.

测度熵；拓扑熵；序列熵；旋转熵；拓扑压；可交换性

1 预备知识

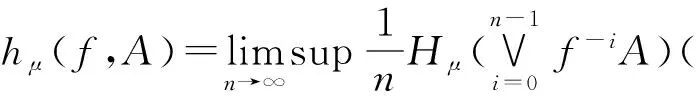
1967年，Kusnhirenko A在文献[3]中给出了测度序列熵的定义.

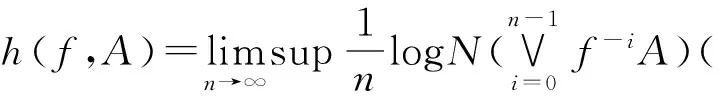
1974年，Goodman TNT在文献[4]中给出了拓扑序列熵的定义.

引理1[5]若A是X的一个有限的开覆盖，f:X→X是连续映射,则N(A)=N(f-1(A))(此处N(A)为从A选取的有限覆盖的最小基数).

证明 见文献[5].

证明 对于μ∈M(X)和E∈β(X)，有

命题2 若记

由命题1和命题2，很容易得到：

命题4 把命题2中的M(X,f∘g)换成遍历可测集E(X,f∘g)，有同样的结果.

2 几类熵的可交换性

2.1 测度熵的可交换性

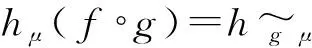
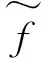
推论1 若μ∈Μ(X,f)∩Μ(X,g)，则有hμ(f∘g)=hμ(g∘f).

若记Mmax(X,f)为连续映射f:X→X最大熵的可测集，则有：

由命题2和定理1得到定理2.

2.2 拓扑熵的交换性

定理3[1]若f,g:X→X是连续映射，则有h(f∘g)=h(g∘f).

余下的证明与定理3类似.

2.3 条件拓扑熵的交换性

定理4 若f,g:X→X是同构，则有h*(f∘g)=h*(g∘f).

2.4 二维映射熵的可交换性

记F:X×X→X×X(X是紧的)，对∀(x,y)∈X×X，有F(x,y)=(f(x),g(y)),当X=[0,1]时，它有一个Sharkovskii型的序[7].

命题6 若F:X×X→X×X，则有h(F)=h(f∘g)=h(g∘f).

证明 考虑F2(x,y)=(f∘g(x),g∘f(y)).

由f:Xi→Xi,i=1,2，则由h(f1×f2)=h(f1)×h(f2)[8]和命题5知，h(F2)=2h(f∘g)+2h(g∘f)，众所周知,(X,f)是紧系统时,拓扑熵满足性质ent(fm)=m·ent(f)[9],知h(F)=h(f∘g)=h(g∘f),再由h(F2)=2h(F)即得结论.

2.5 旋转熵的可交换性

1999年， GELLER W和MISIUREWICZ M在文献[10]中定义了旋转熵.

υ∈Rd，此时的旋转熵定义为hυ(f,φ)=sup{hμ(f):μ在υ方向遍历}.

证明 令E=suppμ，于是E=suppμ闭，且μ(E)=1，f-1(E)=β(X)，则gμ(f-1(E))=μ(g-1(f-1E)))=μ(g-1(f-1(E)))=μ(f∘g)-1(E))=μ(E)=1.

证明 由定理1和引理3即得.

2.6 拓扑压的可交换性

命题7 若f,g:X→X，φ:X→R连续，则P(f∘g,φ)=P(g∘f,φ∘f).

证明

推论3 如果M(X,g∘f)=Μ(X,f)，则P(f∘g,φ)=P(g∘f,φ).

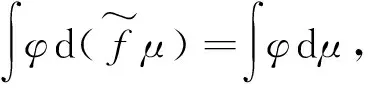
相反方类似证明.

易知Mφ(X,f∘g)=Φ当且仅当Mφ∘f(X,g∘f)=Φ.

[1] KOLYADA S,SNOHA L.Topological Entropy of Nonau-tononous Dynamical Systems[J].Random Comput Dyn,1996(4):205-233

[2] BALIBREA F,CANOVAS PENA J S,JIMENZ LOPEZ V.Commutativity and Non-commutativity of Topological Seque-nce Entropy[J].Ann Inst Fourier(Grenoble),1999,49(5):1693-1709

[3] KUSHNIRENKO A G.On Metric Invariants of Entropy Type[J].Russ Math Surv,1967(22):53-61

[4] GOODMAN T N T.Topological Sequence Entropy[J].Proc London Math Soc,1974，29 :331-350

[5] WALTERS P.An Introduction to Ergodic Theory[M].Springer-Verlag，1982

[6] MISIUREWICZ M.Topological Conditional Entropy[J].Studia Math,1976,55:175-220

[7] BLOKH A.The Spectral Descomposition for One-Dimensi-onal Maps[M].Springer-Verlag,1995

[8] ROKLIN V.On the Antropy of a Metric Automorphism[C]∥Dokl Akad Nauk SSSR.1959:980-983

[9] ADLER R L,KONHEIM A G,MCANDREW J M H.Topological Entropy[J].Trans Amer Math Soc,1965(114):309-319

[10] GELLER W,MISIUREWICZ M.Rotation and Entropy[J].Trans Am Math Soc,1999(351):2927-2948

[11] LEMANCZTCZ M.The Sequence Entropy for Morse Shifts and Some Counter Examples[J].Studia Math,1985,82:221-241

[12] 罗纳.一类非扩张型映象不动点定理的推广[J].重庆工商大学学报(自然科学版),2013,30(12):14-17

LUO N.An Expansive Image Promotion of Fixed Point Theorem[J].Chongqing Technology and Business Univer-sity(Natural Science Edition),2013,30(12):14-17

责任编辑：李翠薇

On the Commutativity of Entropy

ZOU Cheng

(Sichuan College of Chemical Technology, Sichuan Luzhou 646005, China)

Regardless of a measurement space or a topological space, after two consecutive mappings composite, their entropy is correlated to the composite order, however, when some conditions are met, some of composite orders can be exchanged but the entropy keeps constant after the orders are exchanged. This paper reviews in detail the definitions related to the entropy, and discusses the commutativity of the metric entropy after the composite of two mappings, metric sequence entropy, topological entropy, topological sequence entropy, topological entropy of two-dimensional mapping, rotational entropy and topological pressure.

metric entropy; topological entropy; sequence entropy; rotational entropy; topological pressure; commutativity

10.16055/j.issn.1672-058X.2017.0001.010

2016-01-08；

2016-05-25.

邹成(1974-)，男，四川宜宾人，副教授，硕士，从事拓扑学及数学教育的研究.

O189

A

1672-058X(2017)01-0048-04