一种解可分凸优化问题的外梯度并行分裂算法*

程 鹏

(重庆师范大学 数学科学学院, 重庆 401331)

一种解可分凸优化问题的外梯度并行分裂算法*

程 鹏

(重庆师范大学 数学科学学院, 重庆 401331)

并行分裂法是求解两个可分离变量线性约束凸优化问题的重要方法,该方法通常要求两个凸函数有邻近映射，对于其中一个函数具有邻近映射，另一个函数光滑但不具有邻近映射的情况,此处提出了一种基于并行分裂的外梯度算法,并在假设光滑函数梯度Lipschitz连续条件下证明了该算法的O(1/ε)迭代复杂度。

凸优化;可分离结构;增广拉格朗日法;并行分裂法

可分离变量的线性约束可分凸优化问题，是研究数学、工程科学和管理科学的一个重要工具，其目标函数是可分离函数的和，且约束是线性约束。

He B S[1]给出了求解含两个可分离变量的凸优化问题的并行分裂增广拉格朗日算法，这个算法能够很好地利用问题的可分离结构，因此在应用领域得到了大家的广泛认可。在此基础上许多读者提出了各种改进算法，如邻近点并行分裂算法[2]、非精确并行分裂算法[3]、预测校正并行分裂算法[4]等。Gabay D及Mercier B[5]提出的交替方向分裂法也是求解可分凸优化问题的一种有效方法，根据交替方向法的求解优势,Chen G和Teboul M等人[6-8]通过求解一系列凸极小化问题得出了一种改进的交替方向法，Ma S Q, et al[9]对于只有一个目标函数有邻近映射的优化问题提出了基于外梯度的交替方向分裂法。受He B S[1]和Ma S Q[9]的启发，此处提出基于外梯度的并行分裂算法。

1 预备知识

这篇文章中考虑以下凸规划约束模型：

minf(x)+g(y)

s.t.Ax+By=b

x∈X,y∈Y

(1)

其中f和g是凸函数,X∈Rn,Y∈Rp,A∈Rm×n,B∈Rm×p,b∈Rm，X和Y是凸集且在它们上的投影很容易求得。求解问题(1)通常采用经典的增广拉格朗日法(ALM)，产生的迭代格式如下：

其中L(x,y,λ)是问题(1)的增广拉格朗日函数，定义为

λ是与线性约束Ax+By=b有关的拉格朗日乘子，γ是罚参数。

2009年，He B S[1]等人提出关于两个可分离凸优化问题的并行分裂算法迭代如下：

(2)

受文献[9]的启发，此处提出了外梯度并行分裂法并在假设函数梯度满足lipschitz连续的条件下证明了ε最优解的迭代复杂度。

2 外梯度并行分裂算法

若f,g均容易求得邻近映射，则问题(1)用迭代步骤(2)可以求得。这部分考虑函数f有邻近映射，函数g光滑但不容易得到邻近映射的情况，提出以下的基于外梯度的并行分裂增广拉格朗日法解决问题(1)。以任意初始点y0∈Y，λ0∈Rm开始，迭代形式如下：

(3)

L(x,y,λ)=f(x)+g(y)-λT(Ax+By-b)

所以式子(3)中第一个子问题可以表示为

因为光滑凸函数g不容易求解，所以优化问题miny∈YLγ(x,y,λ)对于给定的x和λ也不容易求解，因此在外梯度并行分裂增广拉格朗日法中不能直接求解miny∈YLγ(x,y,λ)。采用的方法是固定x和λ，用拉格朗日函数投影步去校正y。

关于λ,拉格朗日函数L(x,y,λ)的梯度为

▽λL(x,y,λ)=-(Ax+By-b)

关于λ的两个迭代步为

▽λL(xk,yk,λk)

因此式(3)等价于:

(4)

3 算法的迭代复杂度

这部分分析新方法的迭代复杂度，证明在假设光滑函数g的梯度满足Lipschitz连续条件下，式(3)对于式(1)在O(1/ε)迭代内找到一个ε最优解,问题(1)的对偶问题为

(5)

下面定义式(1)的ε最优解。

(6)

其中，x*×y*是式(1)的最优解，Λ*是对偶问题(5)的最优解。

(7)

证明 由式(4)的子问题，有

(8)

所以：

(9)

第2个式子和第4个式子求和可以变形为

所以：

(10)

结合式(9)(10)得:

其中，

因此有

(11)

令y=yk+1,λ=λk+1，则有

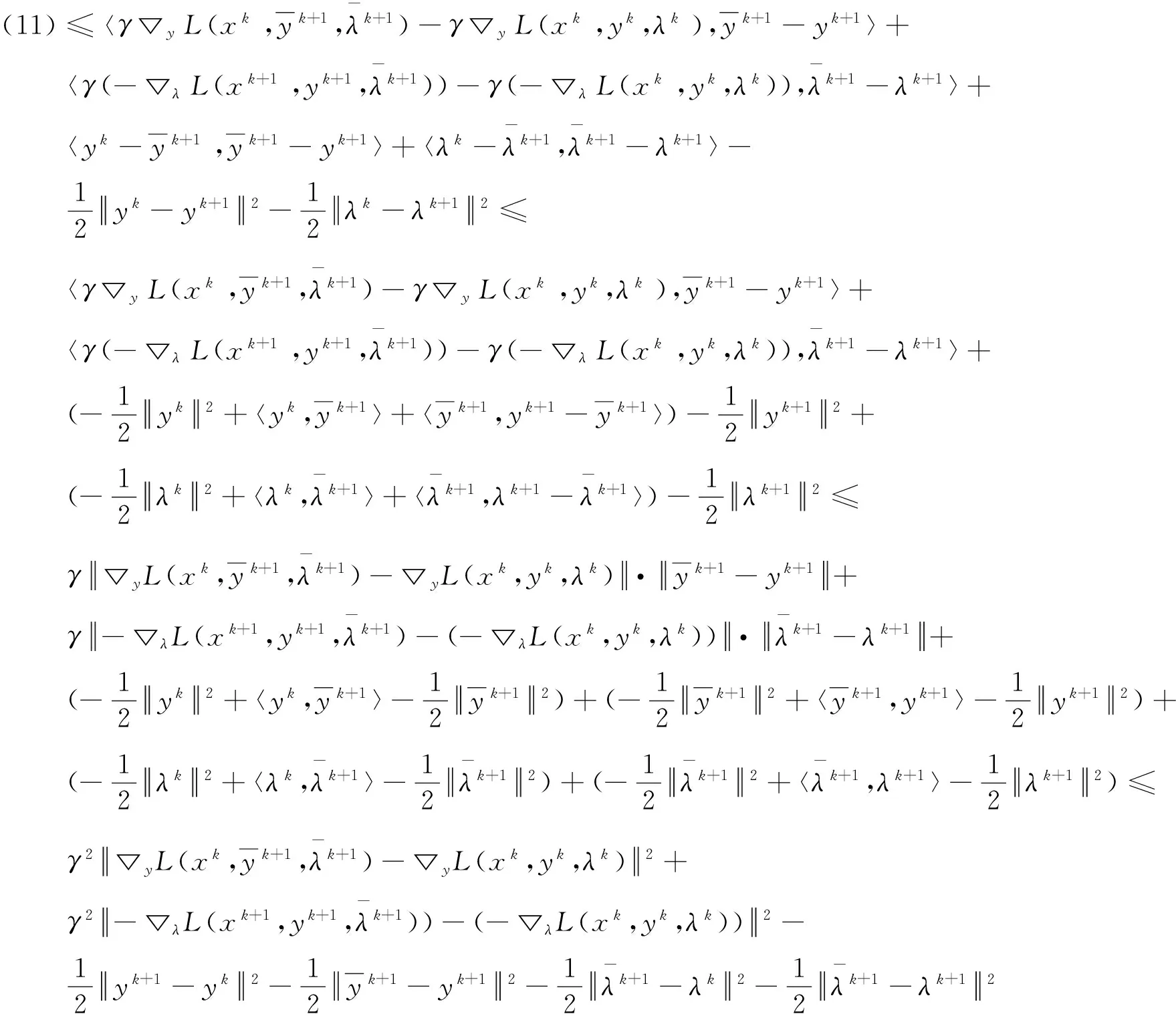
引理1得证。

引理2 假设▽g(y)是Lipschitz连续，Lg是Lipschitz常数，则有

∀y1,y2∈Y

(12)

证明 对于∀y1,y2∈Y,∀λ1,λ2∈Λ，有

结合引理1则引理2得证。

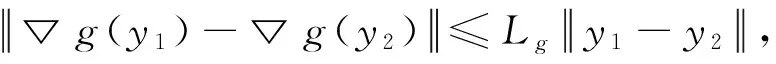
(14)

证明 式(8)中的第3个式子和第4个式子求和得：

(15)

(16)

因此引理3得证。

(17)

证明 由式(3)中关于x的子问题的最优性条件：

〈∂f(xk+1)-ATλK+γAT(Axk+1+Byk-b)+

H(xk+1-xk),x-xk+1〉≥0，x∈X

▽λL(xk,yk,λk)

=λk-γ(Axk+Byk-b)

所以可以得到:

γATA(xk+1-xk),x-xk+1〉≥0,x∈X

结合引理3，有

因为

〈(H+γATA)(xk-xk+1),x-xk+1〉=

(18)

当k=0,1，…,N时，对式(18)求和，有

(19)

L(x,y,λN)-L(xN,yN,λ)

因此得到：

因为x*,y*,λ*有界且N=O(1/ε)，所以可以保证：

4 结 论

提出了求解具有特殊结构的可分离凸优化问题(1)的一种外梯度并行分裂算法,与文献[1]提出的并行分裂算法相比，本文提出的方法可以求解可分离的目标函数没有邻近映射的情况，并在假设另一个函数的梯度满足Lipschitz连续的条件下，证明了该算法的O(1/ε)迭代复杂度。

[1] HE B S.Parallel Splitting Augmented Lagrangian Methods for Monotone Structued Variational Inequalities[J].Computational Optimization and Applications,2009(42):195-212

[2] HAN D,HE H J,XU L L.A Proximal Parallel Splitting Method for Minimizating Sum of Convex Functions with Linear Constraints[J].Journal of Computational and Applied Mathematics,2014(256):36-51

[3] PENG Z,WU D H.An Inexact Proximal Alternating Directions Method for Monotone Structured Variational Inequalities[C]∥Proceedings of the International MultiConference of Engineers and Computer Scientists.2010:1977-1984

[4] 王凯.解可分离凸优化的两个并行分裂算法[D].南京:南京师范大学,2012 WANG K.Two Parallel Splitting Algorithms for Solving Separable Convex Optimization[D].Nanjing:Nanjing Normal University,2012

[5] GABAY D,MERCIER B.A Dual Algorithm for the Solution of Nonlinear Variational Problems via Finite-Element Approximations[J].Computers Mathematics with Applica-tions,1976(2):17-40

[6] CHEN G,TEBOULLE M.A Proximal-Based Decomposition Method of Convex Minimiaztion Problems[J].Mathematical Programming,1994(64):81-101

[7] HE B S,YANG H,ZHANG C S.A Modified Augmented Lagrangian Method for a Class of Monotone Variational Inequalities[J].European Journal of Operational Research,2004(159):35-51

[8] ROCKAFELLAR R T.Augmented Lagrangians and Applications of the Proximal Point Algorithm in Convex Programming[J].Mathematics of Operations Research,1976(1):76-112

[9] MA S Q,ZHANG S Z.An Extragradient-Based Alternating Direction Method for Convex Minimization[J].Foundations of Computational Mathematics,2015(1):1-25

[10] 刘川何.求解分裂可行问题的一种松弛投影算法[J].重庆工商大学学报(自然科学版),2016(1):16-18

LU C H.A Relaxation Projection Algorithm for Solving the Split Feasibility Problem[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2016(1):16-18

责任编辑：李翠薇

An Extragradient Parallel Split Algorithm for Solving Separable Convex Optimization Problem

CHENG Peng

(College of Mathematics,Chongqing Normal University, Chongqing 401331, China)

Parallel splitting method is an important method for solving the convex optimization problem with two separable variables.The methods usually requires that the two convex functions have relatively easy proximal mappings, for the structure that only one of the two functions has easy proximal mapping and the other one is smoothly convex but does not have an easy proximal mapping.We propose in this paper an extragradient algorithm based on parallel splitting.Under the assumption that the smooth function has a Lipschitz continuous gradient condition, we prove theO(1/ε)iterationcomplexityofthemethod.

convex optimization; separable structure; augmented Lagrangian method; parallel splitting method

10.16055/j.issn.1672-058X.2017.0000.007

2016-05-03；

2016-06-25.

重庆市自然科学基金(CSTC2015JCYJBX0029).

程鹏(1990-),女，重庆垫江人，硕士研究生，从事最优化理论与应用研究.

O224

A

1672-058X(2017)01-0034-07