镁合金低周疲劳寿命预测模型探讨

陈 凌 张贤明 刘 飞 欧阳平 贾艳艳

1.重庆工商大学废油资源化技术与装备工程研究中心，重庆,4000672.重庆大学机械工程博士后科研流动站，重庆,4000443. 重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆,400067

镁合金低周疲劳寿命预测模型探讨

陈 凌1,2张贤明1刘 飞2欧阳平1贾艳艳3

1.重庆工商大学废油资源化技术与装备工程研究中心，重庆,4000672.重庆大学机械工程博士后科研流动站，重庆,4000443. 重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆,400067

通过铸造镁合金AZ91D和变形镁合金AZ31B室温环境下应力控制的低周疲劳试验，采用Basquin模型、SWT模型、应变能-寿命模型等模型进行了镁合金低周疲劳的寿命预测。在此基础上，基于连续介质损伤力学的不可逆热力学理论，将镁合金的低周疲劳损伤视为一个不可逆的耗散过程，用熵来反映系统的耗散过程，并以每一次循环的平均应变增量来反映平均应力对材料的影响，提出了一种新的镁合金低周疲劳寿命预测模型。用该模型进行了镁合金的低周疲劳寿命预测，预测结果与实测结果符合较好，同时相比上述其他模型，该模型具有较好的预测效果。

镁合金；低周疲劳；疲劳寿命；熵；平均应力

0 引言

近年来，随着国家对汽车油耗、排放和汽车轻量化的逐渐重视，镁合金在汽车领域得到了广泛的应用。疲劳是汽车结构件发生损坏的主要形式之一，镁合金的低周疲劳寿命预测对于镁合金结构及零部件的工程设计和优化有着较为重要的意义。目前，关于镁合金低周疲劳的研究主要集中在低周疲劳的失效机理以及稀土等添加元素对材料疲劳性能的影响等方面[1-6]，关于低周疲劳寿命预测的研究则较少，主要以经典的Manson-Coffin模型[7]、Basquin模型[8]以及在此基础上的一些修正为主[9-12]，缺乏系统深入的研究，预测精度受镁合金类型、工况等影响较大，尤其是非对称应力控制下的低周疲劳。

针对上述情况，本文通过铸造镁合金AZ91D和变形镁合金AZ31B室温环境下应力控制的低周疲劳试验，考察了Basquin模型[8]、SWT(Smith Wastson Topper)模型[9]、应变能-寿命模型[13]等模型对于镁合金低周疲劳寿命的预测效果。在此基础上，基于连续介质损伤力学中的不可逆热力学理论，将镁合金的低周疲劳损伤视为一个不可逆的耗散过程，用熵来反映系统的耗散过程，并以每一次循环的平均应变增量来反映平均应力对材料的影响，提出了一种新的镁合金低周疲劳寿命预测模型。为验证本文所述模型的预测效果，用该模型进行了镁合金的低周疲劳寿命预测，并与上述其他模型的预测效果进行了对比。

1 镁合金低周疲劳寿命预测模型

目前，镁合金的低周疲劳寿命预测以经典的Manson-Coffin模型[7]、Basquin模型[8]为主，Manson-Coffin模型用于应变控制的低周疲劳寿命预测，Basquin模型用于应力控制的低周疲劳寿命预测。

Manson-Coffin模型的表达式为

(1)

Basquin模型的表达式为

(2)

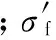
在Manson-Coffin模型和Basquin模型的基础上，针对镁合金的低周疲劳寿命预测，有学者提出了相应的修正模型[9-12]，其中应用较多且较为典型的为SWT模型[9]。SWT模型用等效应力σeq代替Basquin模型(式(2))中的名义应力幅σa，并在σeq上考虑平均应力的影响，其表达式如下：

(3)

式中，R为应力比。

在实际的应用中，由于镁合金成形工艺的不同，铸造镁合金和变形镁合金的性能有较大差异，如变形镁合金具有更好的塑性，同时具有明显的各向异性。对于不同类型的镁合金，Manson-Coffin模型、Basquin模型、SWT模型的预测效果不同。另外，材料初始损伤程度、工况条件等对于上述模型也有较大影响，尤其是当材料具有初始损伤时，运用上述模型进行镁合金的低周疲劳寿命预测，将出现较大的偏差。

除上述模型外，有研究将低周疲劳寿命预测中的应变能-寿命模型用于镁合金的低周疲劳寿命预测[13]。应变能-寿命模型认为材料的低周疲劳损伤主要是由塑性变形引起的，塑性变形积累到一定程度时，材料发生失效。用塑性应变能密度反映材料的塑性变形，可得塑性应变能-寿命模型如下：

(4)

式中，ΔWP为塑性应变能密度，通常取为半寿命处的塑性应变能密度;α、C为材料常数。

式(4)中的塑性应变能密度可通过下式进行计算[14]：

(5)

也可通过计算迟滞回线所围面积得到。其中，Δσ为名义应力范围;Δεp为塑性应变范围;n′为循环应变硬化指数。

在塑性应变能-寿命模型的基础上，考虑循环加载过程中平均应力的影响，用弹性应变能密度反映平均应力的影响，并用总应变能密度代替式(4)中的塑性应变能密度，可得总应变能-寿命模型如下：

(6)

式中，ΔWt为总应变能密度;ΔWe为弹性应变能密度;α′、C′为材料常数。

式(6)中的弹性应变能密度考虑平均应力的影响，计算公式如下[15]：

(7)

式中，σm为平均应力。

相对于Manson-Coffin模型、Basquin模型、SWT模型等模型，应变能-寿命模型对于镁合金的低周疲劳寿命预测具有更好的适应性，但由于平均应力存在时棘轮效应对材料损伤有影响，因此应变能-寿命模型对于非对称应力控制下的镁合金低周疲劳预测效果出入较大，尤其是平均应力较大的工况。

2 一种新的镁合金低周疲劳寿命预测模型

材料低周疲劳的损伤演化与加载的主方向密切相关，由于镁合金尤其是变形镁合金具有明显的各向异性，导致损伤主方向和主应力方向不一定相同，使得损伤主轴和损伤主值不断发生变化，导致镁合金低周疲劳损伤的研究难度较大。

根据连续介质损伤力学理论，对于各向异性材料的疲劳损伤[16]，应选用合适的损伤内变量描述材料的损伤状态，并基于不可逆热力学建立材料的本构方程和损伤演化方程。

根据连续介质损伤力学中的不可逆热力学理论，镁合金的低周疲劳损伤可视为一个不可逆的耗散过程，可通过损伤内变量即耗散变量来描述材料的损伤过程。另外，热力学系统的耗散导致系统的熵产生，可用熵来反映系统的耗散过程。同时，对于热力学系统来说，熵的产生满足熵守恒定律[17]，即系统总熵等于环境供给熵与系统内部产生熵之和，具体可以用下式表示：

(8)

其中，S*为单位质量内部产生的熵；s为单位质量熵；ρ为物体密度；T为绝对温度；γ为单位质量热供给；h为热通量。同时，式(8)中由温度梯度gradT引起的热力学系统耗散为热耗散，剩余的热力学系统耗散为内禀耗散。

根据连续介质损伤力学中的不可逆热力学理论，将能量守恒的局部表达式[17]

(9)

代入式(8)，可将式(8)改写为下式：

(10)

式中，e为单位质量的内能;σ为应力张量;ε为应变张量。

对于一定温度下的低周疲劳过程来说，式(10)中的温度梯度gradT为零，其熵增与内能变化仅与疲劳载荷所做机械功相关，同时疲劳载荷所做机械功可用总应变能进行反映，将式(10)改写如下：

(11)

式中，W为机械功;ηW为应变能的内熵增量(单位质量内部产生熵)转化率。

对于热力学系统来说，其单位质量内部产生的熵S*即内熵增量为总熵增量中的不可逆部分。将材料的低周疲劳损伤过程看成是内熵增量不断增加的过程，当内熵增量增加到临界值时，材料发生失效。同时，对于相同工况条件下的低周疲劳来说，材料发生失效时的内熵增量临界值是一定的。按此理论，对式(11)进行积分，可得

(12)

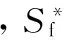
对于对称载荷控制下的低周疲劳来说，材料的损伤与每次加载产生的塑性变形相关；对于非对称应力控制下的低周疲劳来说，材料的损伤除与每次加载产生的塑性变形相关外，还受平均应力造成的棘轮效应即循环蠕变的影响，较对称载荷来说，损伤过程较为复杂。研究表明[18-19]，棘轮效应对疲劳寿命的影响主要为循环蠕变造成的应变积累。对于非对称应力控制下的低周疲劳，每一循环的损伤包括疲劳载荷和循环蠕变两部分，两者相互耦合，使得材料的塑性变形不断累积。同时材料的内熵增量同材料的塑性变形相关，当塑性变形达到一定程度时，材料内熵增量达到临界值导致材料失效。

对于非对称应力控制下的低周疲劳来说，通常用平均应变εm的变化来反映循环蠕变的影响，因此，可认为循环过程中的内熵增量同每一循环过程中的塑性应变范围Δεp和平均应变增量Δεm相关，定义ηW如下：

(13)

其中，Δεt为每一循环过程中的总应变范围，同时为便于计算，定义函数η为power函数，将式(13)改写如下：

(14)

式中，β为材料常数。

将式(14)代入式(12)，可得

(15)

如前所述，对于相同工况条件下的低周疲劳来说，材料发生失效时的内熵增量临界值是一定的，因此，对于选定的镁合金材料，在一定的温度环境下，式(15)中的材料常数A是一定值。在实际应用中，选取半寿命处的疲劳参数为均值，即可得到一种新的镁合金低周疲劳寿命预测模型如下：

(16)

式中，ΔWtNf为循环总应变能积累；(Δεp+Δεm)/Δεt为内熵增量转化参量；Δεp、Δεm、Δεt、ΔWt分别为半寿命处的塑性应变范围、平均应变增量、总应变范围和总应变能密度。

3 试验结果及讨论

试验在电液伺服疲劳试验机上进行，试验温度为恒定室温25℃。试验用镁合金材料分别为铸造镁合金AZ91D和变形镁合金AZ31B，其化学成分和室温下的力学性能见表1、表2，其中，σb为抗拉强度、σ0.2为屈服强度、δ为延伸率。试验用疲劳试样采用光滑圆棒试样，按低周疲劳试验标准GB/T15248-2008[20]制作，具体的形状及尺寸见图1。试验采用应力控制，控制波形为三角波，考虑平均应力的影响，应力比选为R=0与R=0.2，加载频率为3～5Hz。

表1 试验用镁合金化学成分(质量分数)

表2 试验用镁合金力学性能表(室温25 ℃)

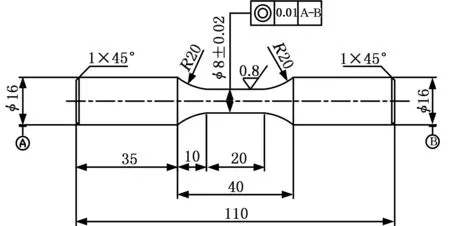
图1 疲劳试样示意图Fig.1 Fatigue specimen in experiments

表3、表4分别为铸造镁合金AZ91D和变形镁合金AZ31B恒定室温25 ℃下的低周疲劳试验数据及试验结果，其中应变、应变能密度等疲劳参数均取为半寿命处的参数值。

基于表3、表4的试验数据，对Basquin模型、SWT模型、应变能-寿命模型以及本文提出的镁合金低周疲劳寿命预测模型进行了拟合，拟合关系式如下，拟合曲线见图2，其中Rf为拟合相关系数。

(1)Basquin模型。

AZ91D：σa=176.17326(2Nf)-0.081，Rf=0.87156

AZ31B：σa=161.57345(2Nf)-0.07681，Rf=0.86453

(2)SWT模型。

AZ91D：σeq=246.55851(2Nf)-0.0732，Rf=0.9302

AZ31B：σeq=229.54614(2Nf)-0.07115，Rf=0.9508

(3)塑性应变能-寿命模型。

(4)总应变能-寿命模型。

(5)新的镁合金低周疲劳寿命预测模型。

AZ91D：

AZ31B：

用上述模型进行了镁合金的低周疲劳寿命预测，预测效果见图3。

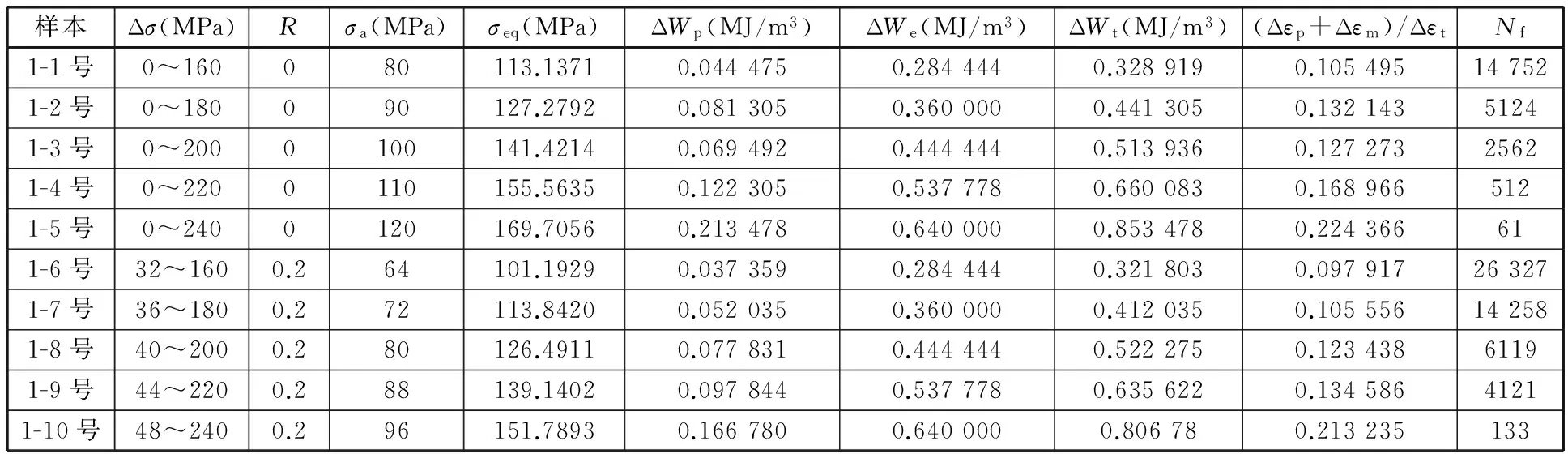
表3 铸造镁合金AZ91D低周疲劳试验数据(室温25 ℃)Tab.3 Low cycle fatigue experiment data of cast magnesium alloy AZ91D at room temperature 25 ℃

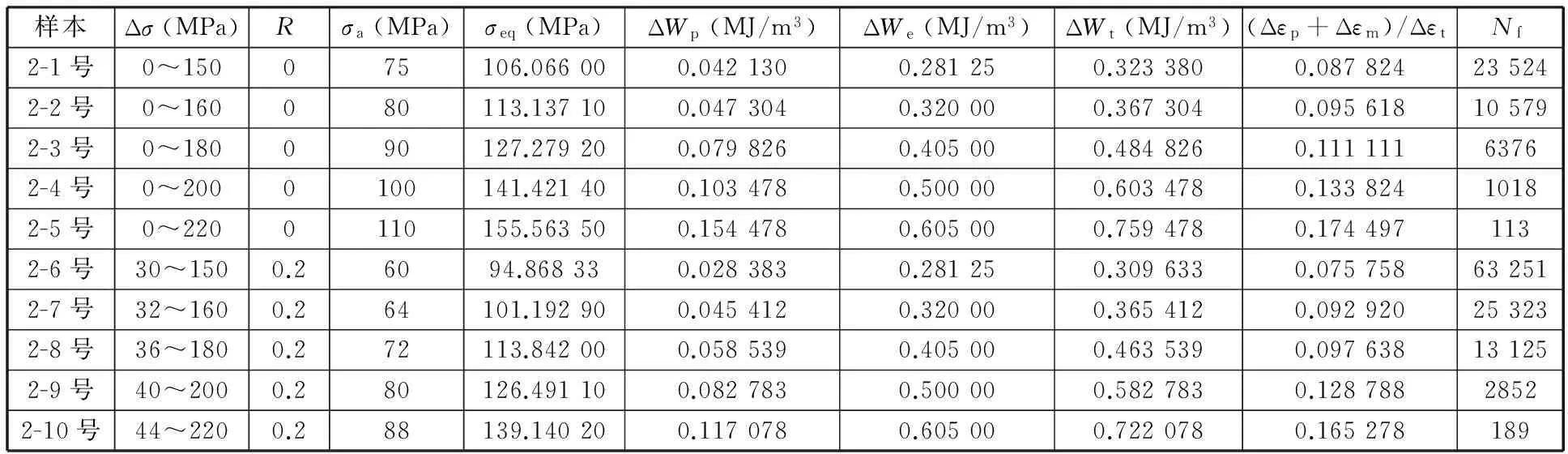
表4 变形镁合金AZ31B低周疲劳试验数据(室温25 ℃)

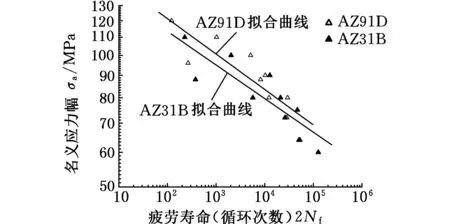
(a)Basquin模型

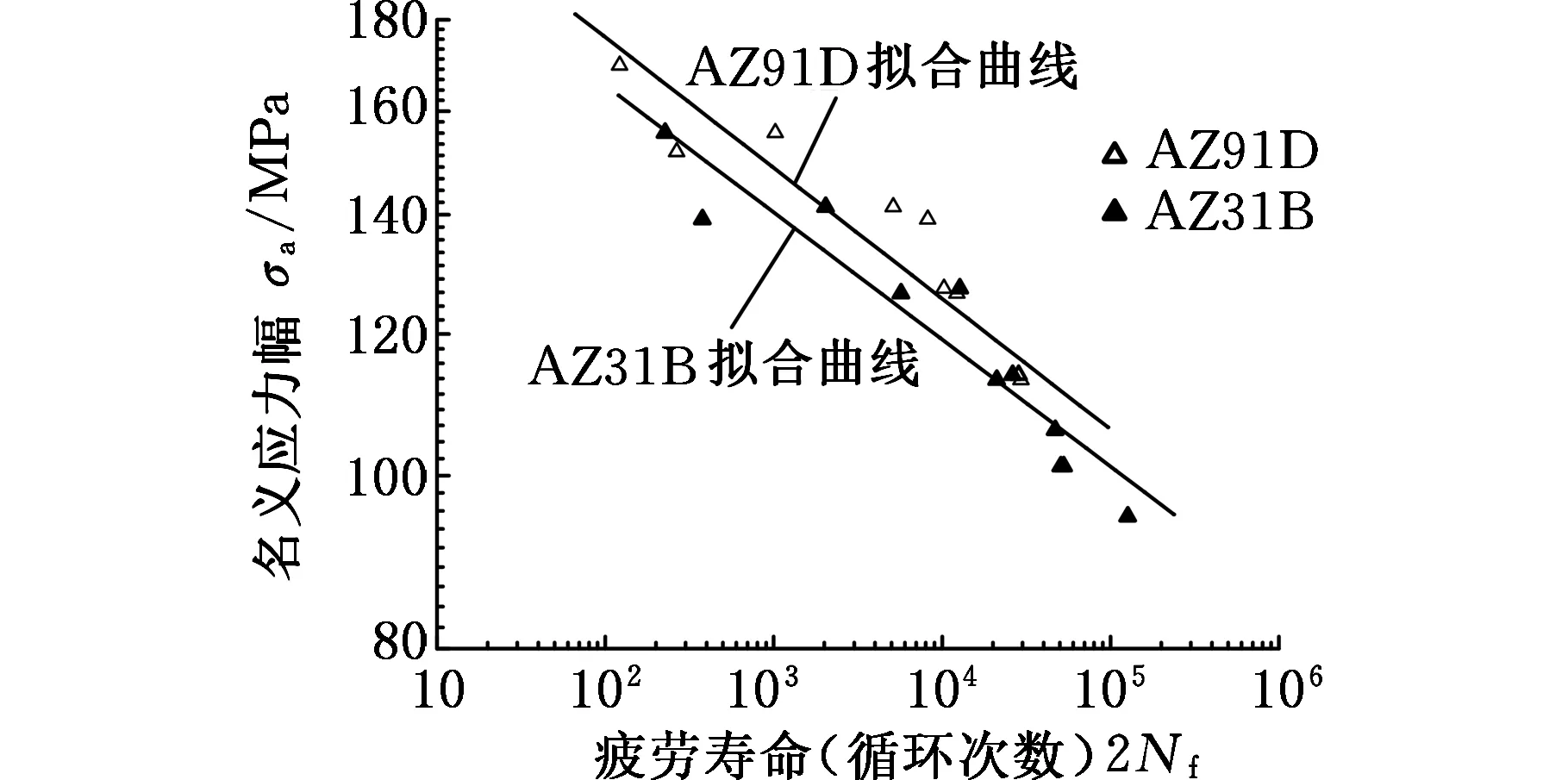
(b)SWT模型

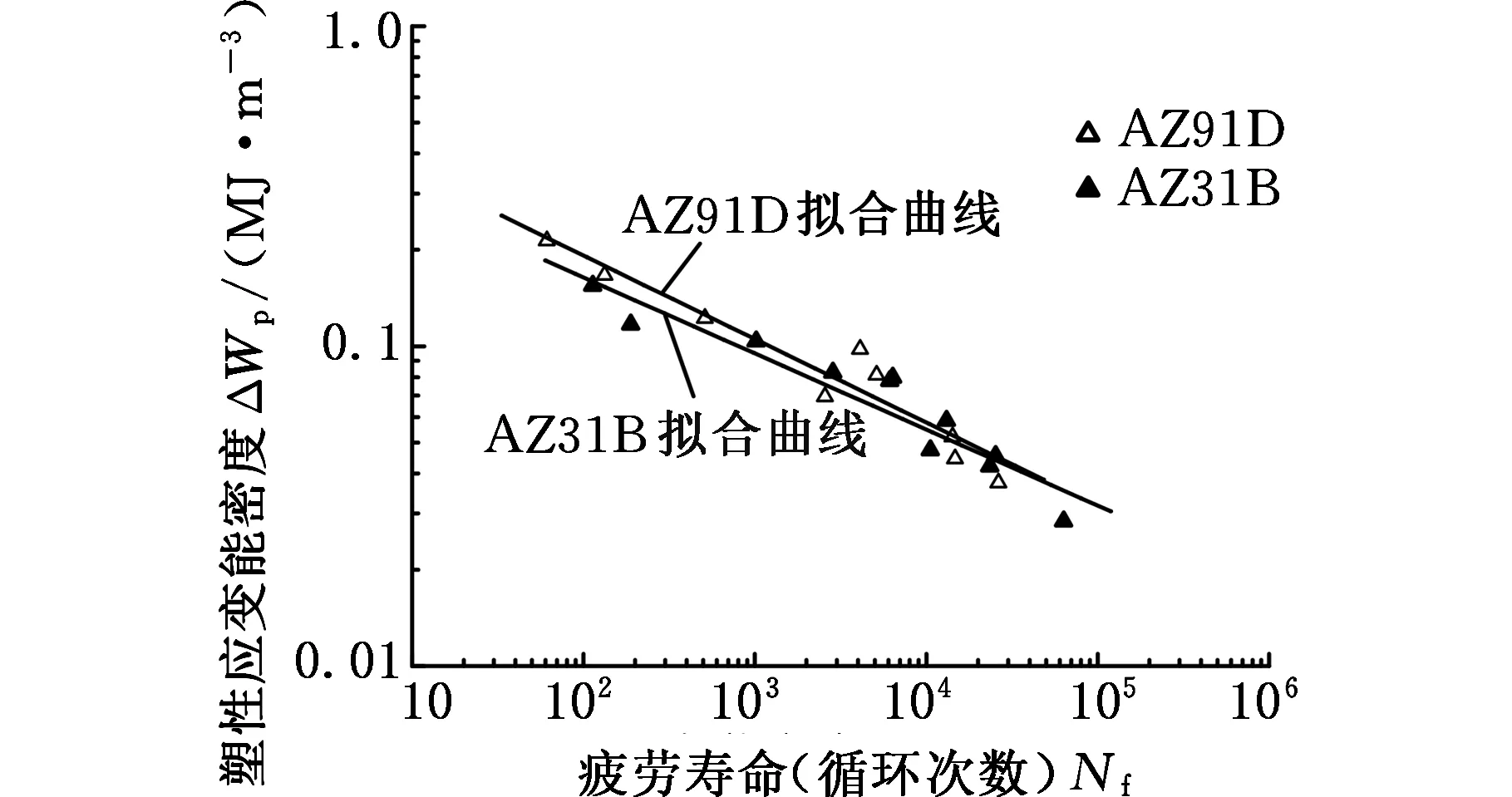
(c)塑性应变能-寿命模型

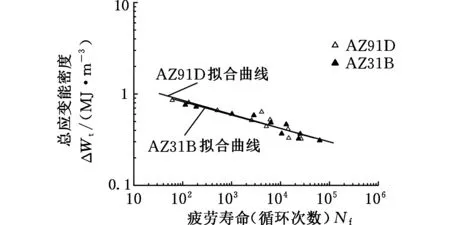
(d)总应变能-寿命模型

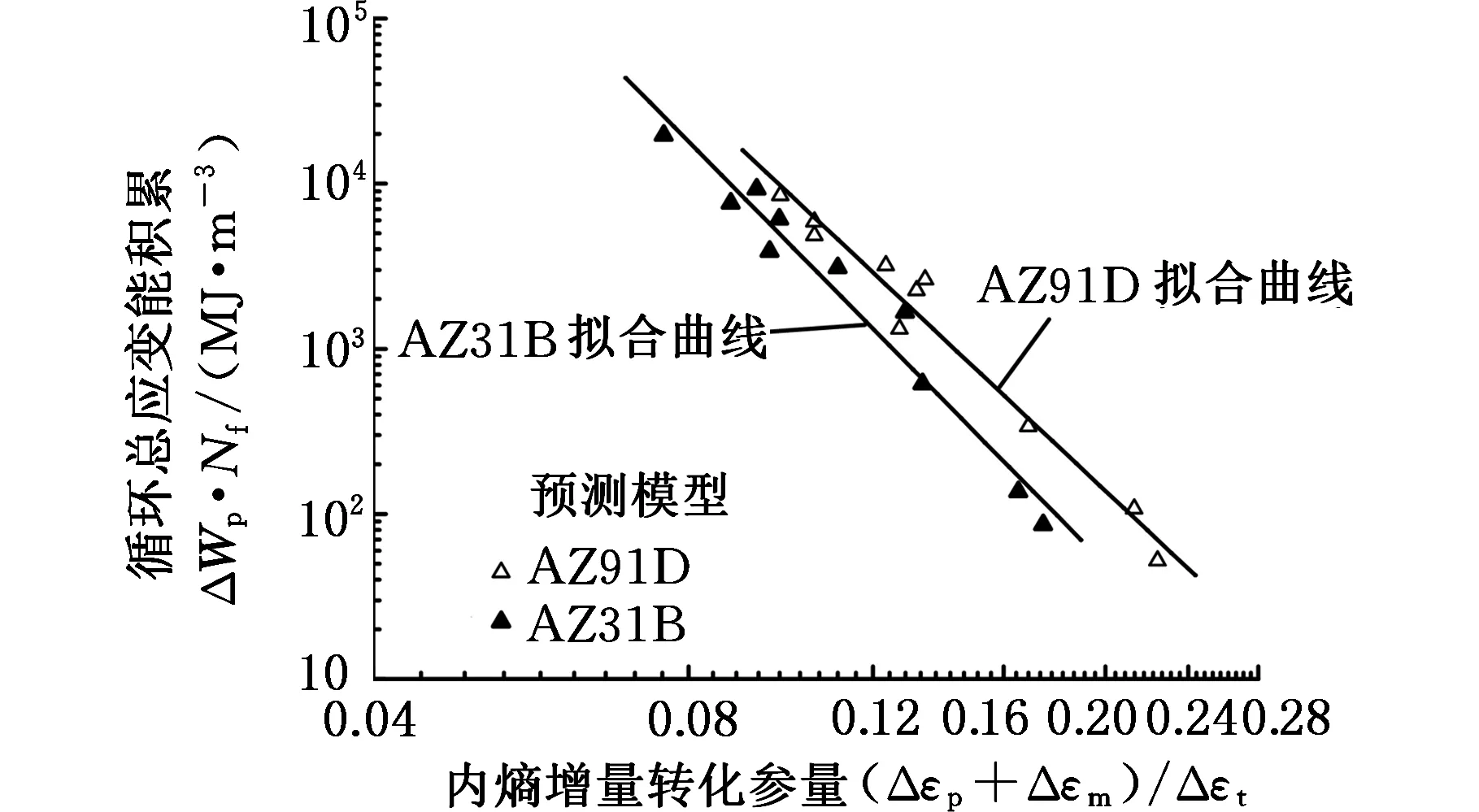
(e)新的镁合金低周疲劳寿命预测模型图2 镁合金低周疲劳寿命预测模型拟合图Fig.2 Fitting curves of low cycle fatigue life prediction models for magnesium alloys

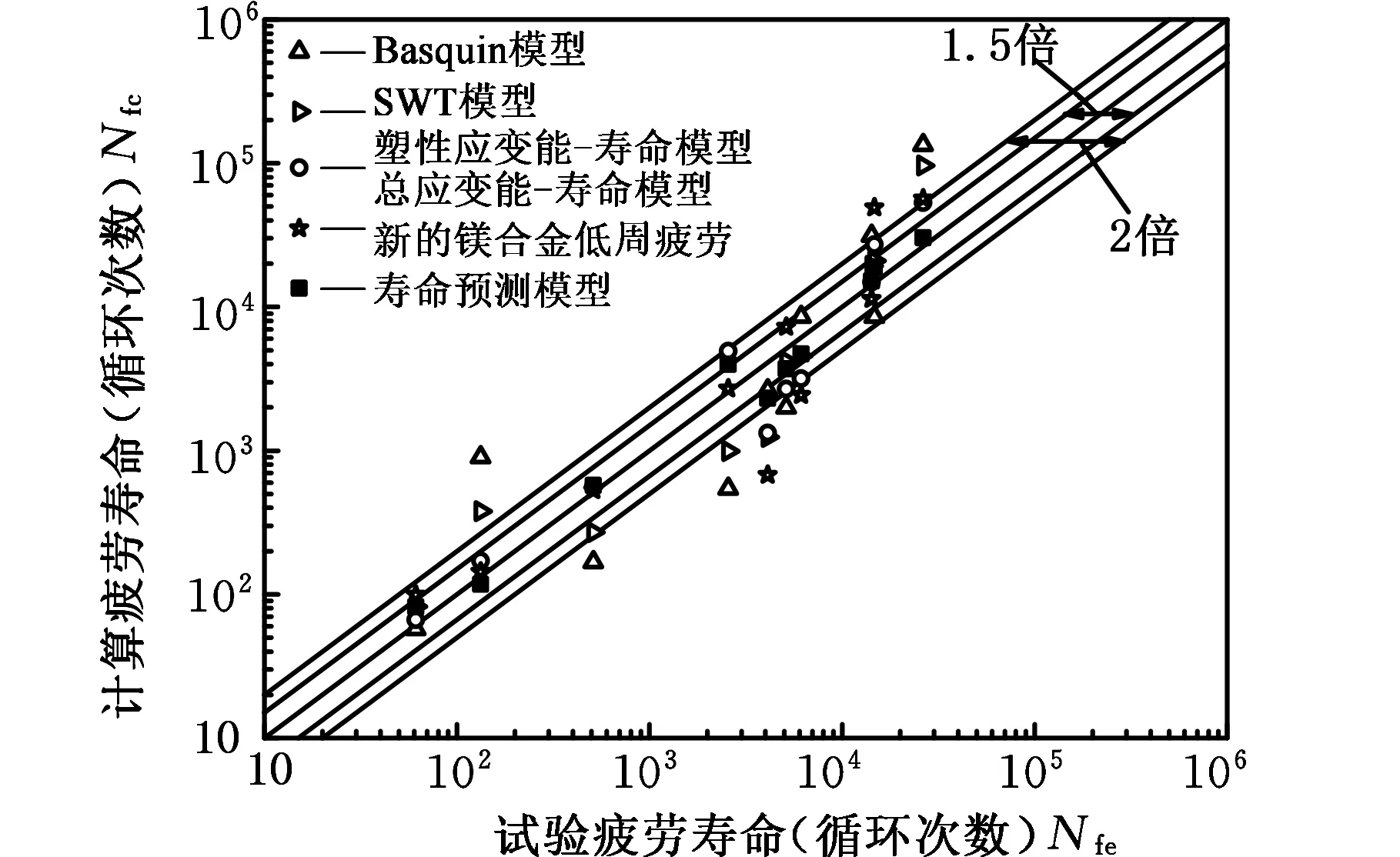
(a)铸造镁合金AZ91D

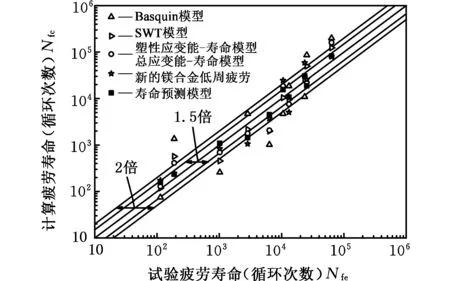
(b)变形镁合金AZ31B图3 镁合金低周疲劳寿命预测效果图Fig.3 Low cycle fatigue prediction effect of magnesium alloys

从图3可知：①相较其他寿命模型，本文提出的镁合金低周疲劳寿命预测模型对于铸造镁合金AZ91D和变形镁合金AZ31B均有较好的预测效果，所有数据点均在2倍误差带以内，大部分数据点在1.5倍误差带以内。②经典的Basquin模型、SWT模型及应变能-寿命预测模型的预测效果有限，仅少部分数据点在1.5倍误差带以内。其中，Basquin模型的预测效果最差，50%以上的数据点在2倍误差带以外，考虑平均应力修正的SWT模型预测效果较Basquin模型预测效果明显改观，仅有少量数据点在2倍误差带以外。相较Basquin模型及SWT模型，应变能-寿命模型预测的整体效果较好，塑性应变能-寿命模型的大部分数据点在2倍误差带以内。

从上述试验结果可知，对于承受非对称应力控制的镁合金低周疲劳而言，经典的Basquin模型、SWT模型及应变能-寿命预测模型的预测效果有限，相较于上述模型，本文提出的镁合金低周疲劳寿命预测模型具有较好的预测效果。同时，本文提出的镁合金低周疲劳寿命预测模型是基于连续介质损伤力学的不可逆热力学理论推导得到的，并以平均应变的变化来反映循环蠕变即平均应力对材料的影响，物理意义明确，模型形式简单，应用方便。

4 结论

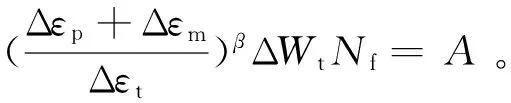
(2)用所推导模型进行了铸造镁合金AZ91D和变形镁合金AZ31B室温(25℃)环境下应力控制的低周疲劳寿命预测，并与经典的Basquin模型、SWT模型及应变能-寿命预测模型进行了比较，结果表明本文提出的镁合金低周疲劳寿命预测模型相比其他模型具有较好的预测效果，预测结果与实测结果符合较好。

[1] LIN Y C, CHEN X M, CHEN G. Uniaxial Ratcheting and Low-cycle Fatigue Failure Behaviors of AZ91D Magnesium Alloy under Cyclic Tension Deformation [J]. Journal of Alloys and Compounds, 2011, 509:6838-6843.

[2] GENG C J, WU B L, DU X H, et al. Low Cycle Fatigue Behavior of the Textured AZ31B Magnesium Alloy under the Asymmetrical Loading [J]. Materials Science & Engineering A, 2013, 560:618-626.

[3] HUANG G S, LI J H, HAN T Z, et al. Improving Low-cycle Fatigue Properties of Rolled AZ31 Magnesium Alloy by Pre-compression Deformation [J]. Materials & Design, 2014, 58:439-444.

[4] MIRZA F A, CHEN D L, LI D J, et al. Low Cycle Fatigue of an Extruded Mg-3Nd-0.2Zn-0.5Zr Magnesium Alloy [J]. Materials and Design, 2014, 64:63-73.

[5] 张思倩, 吴伟, 陈丽丽, 等. 热处理对挤压变形Mg-7%Zn-0.6%Zr-0.5%Y合金低周疲劳行为的影响[J]. 金属学报, 2014, 50(6):700-706. ZHANG Siqian, WU Wei, CHEN Lili, et al. Influence of Heat Treatment on Low-cycle Fatigue Behavior of Extruded Mg-7%Zn-0.6%Zr-0.5%Y Alloy [J]. Acta Metallurgica Sinica, 2014, 50(6):700-706.

[6] ZHU R, CAI X T, WU Y J, et al. Low-cycle Fatigue Behavior of Extruded Mg-10Gd-2Y-0.5Zr Alloys [J]. Materials and Design, 2014, 53:992-997.

[7] COFFIN L F. A Study of Effects of Cyclic Thermal Stresses on a Ductile Metal [J]. Transaction of ASME, 1954, 76:931-950.

[8] WEIBULL W. Fatigue Testing and Analysis of Results [M]. Oxford: Pergamon Press, 1961:184-249.

[9] SMITH R N, WASTON P, TOPPER T H. A Stress-Strain Function for the Fatigue of Metal [J]. Journal of Materials, 1970, 5(4):767-778.

[10] MIROSLAVA H, JOSEF Z, PAVEL D, et al. Evaluation of Fatigue Life of AZ31 Magnesium Alloy Fabricated by Squeeze Casting [J]. Materials and Design, 2013, 45:253-264.

[11] HASEGAWA S, TSUCHIDA Y, YANO H, et al. Evaluation of Low Cycle Fatigue Life in AZ31 Magnesium Alloy [J]. International Journal of Fatigue, 2007, 29:1839-1845.

[12] YU Q, ZHANG J, JIANG Y Y, et al. Effect of Strain Ratio on Cyclic Deformation and Fatigue of Extruded AZ61A Magnesium Alloy [J]. International Journal of Fatigue, 2012, 44:225-233.

[13] SHIOZAWA K, KITAJIMA J, KAMINASHI T, et al. Low-cycle Fatigue Deformation Behavior and Evaluation of Fatigue Life on Extruded Magnesium Alloys [J]. Procedia Engineering, 2011, 10:1244-1249.

[14] TONG X Y, WANG D J, XU H. Investigation of Cyclic Hysteresis Energy in Fatigue Failure Process [J]. International Journal of Fatigue, 1989, 11(5):353-359.

[15] 陈凌. 典型压力容器用钢中高温环境低周疲劳和疲劳蠕变交互作用的行为及寿命评估技术研究[D]. 杭州: 浙江大学, 2007. CHEN Ling.Research on Behavior and Life Assessments of Low Cycle Fatigue and Fatigue-creep Interaction for Typical Pressure Vessel Steels at Elevated and High Temperature [D]. Hangzhou: Zhejiang University, 2007.

[16] 杨光松. 损伤力学与复合材料损伤[M]. 北京: 国防工业出版社, 1995:81-103. YANG Guangsong. Damage Mechanics and Complex Material Damage [M]. Beijing: National Defence Industry Press, 1995: 81-103.

[17] 刘新东, 郝际平. 连续介质损伤力学[M]. 北京: 国防工业出版社, 2011:155-183. LIU Xindong, HAO Jiping. Continuum Damage Mechanics [M]. Beijing: National Defence Industry Press, 2011: 155-183.

[18] 康国政, 李友国. 中碳贝氏体钢的室温单轴循环变形行为研究[J]. 工程力学, 2007, 24(4):173-177. KANG Guozheng, LI Youguo. Uniaxial Cyclic Deformation of Medium Carbon Bainitic Steel at Room Temperature [J]. Engineering Mechanics, 2007, 24(4):173-177.

[19] 李青, 董俊华, 余伟炜, 等. 不同温度下15CrMoR循环塑性实验研究及低周疲劳寿命预测[J]. 机械强度, 2014, 36(3):368-373. LI Qing, DONG Junhua, YU Weiwei, et al. Experimental Study on Cyclic Plasticity and Prediction of Low Cyclic Fatigue Life for 15CrMoR at Different Temperature [J]. Journal of Mechanical Strength, 2014, 36(3):368-373.

[20] 中国国家标准化管理委员会. GB/T 15248-2008 金属材料轴向等幅低循环疲劳试验方法[S]. 北京: 中国标准出版社, 2008. Standardization Administration of China. GB/T 15248-2008 the Test Method for Axial Loading Constant-amplitude Low-cycle Fatigue of Metallic Materials [S]. Beijing: Standards Press of China, 2008.

(编辑 王艳丽)

Discussion of Low Cycle Fatigue Life Prediction Models for Magnesium Alloys

CHEN Ling1, 2ZHANG Xianming1LIU Fei2OUYANG Ping1JIA Yanyan3

1.Engineering Research Center for Waste Oil Recovery Technology and Equipment,Chongqing Technology and Business University, Chongqing，400067 2.Mobile Post-doctoral Research Station of Mechanical Engineering, Chongqing University, Chongqing, 400044 3.Chongqing Key Laboratory of Manufacturing Equipment Mechanism Design and Control, Chongqing Technology and Business University, Chongqing， 400067

Through low cycle fatigue experiments of the cast magnesium alloy AZ91D and the wrought magnesium alloy AZ31B at room temperature under stress control, the fatigue life prediction was conducted by the Basquin model, the SWT model and the strain energy-life model. Then, regarding the low cycle fatigue damage of magnesium alloys as an irreversible dissipation process that might be described by the entropy according to the irreversible thermodynamics theory of continuum damage mechanics, and using the mean strain increment per cycle to reflect the effects of the mean stress, a new model for the low cycle fatigue life prediction of magnesium alloys was developed. By this model, the low cycle fatigue life prediction of magnesium alloys was carried out through the experiments mentioned above. Results show that the predicted results are in good agreement with the experimental results. And compared with the other life prediction models, the new model for the low cycle fatigue life prediction of magnesium alloys has a better effectiveness.

magnesium alloy; low cycle fatigue; fatigue life; entropy; mean stress

2016-04-19

中国博士后科学基金资助项目(2015M582523)；重庆市博士后科研特别资助项目(Xm2016061)；重庆市教委科学技术研究项目(KJ1500624)；重庆工商大学科研启动经费资助项目(2014-56-10)

O346.5；TG115.5

10.3969/j.issn.1004-132X.2017.05.002

陈 凌，男，1979年生。重庆工商大学废油资源化技术与装备工程研究中心高级工程师、博士。主要研究方向为金属材料的疲劳、断裂、腐蚀及机械结构安全评估。发表论文50余篇。授权发明专利15项。E-mail：chenling1618@126.com。张贤明，男，1955年生。重庆工商大学废油资源化技术与装备工程研究中心教授。刘 飞，男，1948年生。重庆大学机械工程学院教授、博士研究生导师。欧阳平，男，1979年生。重庆工商大学废油资源化技术与装备工程研究中心副研究员。贾艳艳，女，1983年生。重庆工商大学制造装备机构设计与控制重庆市重点实验室高级工程师。