神经系统编码时间节律信息的机制

弭元元，胡 岗，吴 思

（1.军事医学研究院军事认知与脑科学研究所，北京 100850；北京师范大学2.物理学系，3.认知神经科学与学习国家重点实验室，北京 100875）

记忆是脑最神奇的高级认知功能之一，泛指神经系统从外界摄取时间和空间信息、编码和储存信息以及在特定条件下再现这些时空信息的过程。了解记忆的神经机制不仅是破译大脑奥秘的关键，同时也是发展人工智能的基础。从20世纪50年代以来，人们对神经系统如何提取和处理外部输入的空间信息已取得了长足进展，如视觉系统中神经元感受野的发现就是一个很好的例子［1］。但人们对神经系统如何提取和处理输入中的时间信息迄今知之甚少［2-5］。

破译人脑记忆活动机制的关键，首先要弄清楚时空信息是如何表达在神经系统的活动中的。人的大脑由大约1×1011个神经元组成，每个神经元平均又有＞1×103的连接，它们构成异常复杂、庞大的网络系统来实现脑的各种高级认知功能，尤其是时空信息的记忆功能。单个神经元的计算功能相对简单（本质上是对输入值的一个整合发放过程）。因此，大脑中与记忆有关的信息表达的奥秘都隐藏在神经网络动力学的计算能力中。大量神经元构成的网络系统的演化本质上是一个复杂系统的动力学过程。因此，对记忆问题的研究吸引了物理学和计算神经科学大量交叉学科领域研究者的兴趣与关注，而物理学家所发展的大量描述复杂系统动力学行为的理论和方法，为研究与记忆相关的脑内神经信息处理机制提供了新的思想，拓宽了研究思路。

基于大脑是通过网络来进行计算的特点，美国理论物理学家Hopfield教授［6］提出了联想式记忆的神经网络模型，开创了将统计物理的思想与技巧（核心是“能量函数”）应用于神经科学研究的新纪元，开启了人工神经网络理论研究的先河。该模型强调信息是存储于网络的动力学吸引子（attractors）态中，即处于网络能量函数极小值所对应的神经元群活动状态。这一吸引子的观点在实验中已得到验证［7］。

以上网络吸引子的思想成功解释了神经系统储存空间信息的很多例子，如头的朝向、物体空间方位等，但目前对神经系统表达时间信息的机制研究甚少。

与空间信息不同的是，在日常生活中，大脑接收到的时间信息的尺度横跨很大的范围，量级从微秒到小时。大脑如何处理不同尺度的时间信息一直以来是饱受争议的话题。目前争论的焦点主要集中在大脑处理这些时间信息是否依赖于一个统一的“时钟”，也就是专门用于记录时间的振荡器（pacemaker）［8］；或无需统一的时钟，而是与该任务相关的局部神经环路即可自动地处理和表征时间信息［2，5，8］。最近的研究表明，在处理数百毫秒级别的时间信息时，神经环路可通过自身的动力学特性来表征时间［9-10］。这些研究通过建立由多种神经元随机连接形成的网络并引入了突触短时程可塑性后发现，随时间不断改变的网络状态本身就可作为介质来存储外界输入的时间序列。进一步研究表明，这些记忆轨迹（memory trace）可用于区分连续事件之间的时间差。但神经网络内在的动力学特性是否能处理秒级以上的时间信息迄今仍不清楚。

近期的一个实验发现，斑马鱼视顶盖的神经环路可记忆以秒为量级的外部周期性视觉刺激的时间间隔［11］。实验中用相同时间间隔的光栅反复对斑马鱼进行刺激，经过数次训练并撤掉刺激后，发现其视顶盖的神经环路可以相同的频率进行自持续的同步发放，且这种自持续的节律行为可诱导斑马鱼的尾部进行有规律的周期摆动。这些现象表明，该神经环路有可能存储节律性输入的感知记忆。在实验中，神经环路所能记忆的最长时间达到了20 s。

神经系统如何获得并存储这种长时程节律信息，一种最直接的假设是大脑中可能存在一个“中央时钟”来计时，从而调控神经网络的周期性响应，然而大量的实验证据表明，大脑中并不存在这样的“中央时钟”［4-5］。那么，生物系统是否可单纯地依赖于神经网络的内在动力学特性即可产生上述观察到的长时程的周期节律信息的记忆？由于单个神经元和突触的时间常数很短，不足以维持这种长时间的行为，那么是否存在具有某种特殊拓扑结构的神经网络呢？回答这一问题对理解脑处理时间信息的机制具有重要的启示。本课题组近期研究发现，具有无标度拓扑结构的大尺度神经网络可实现这样的功能［12］。本文综述了此项研究进展，为理解神经系统编码时间节律信息的机制提供新的思路。

1 神经网络模型

构建的大尺度神经网络模型［12］考虑了无标度的特殊拓扑结构［13］。无标度结构是指网络中神经元连接度的概率分布服从幂率分布，即p（k）≈k-γ（γ为常数）。实际上，该模型不必完全满足无标度结构，只需使得网络中少数神经元的连接度数较大，而多数神经元的连接度数较小。其中，k＞kth的神经元称为枢纽神经元（hub），其他神经元为低连接度神经元（low-degree neuron）。

单个神经元的动力学如下［14］：

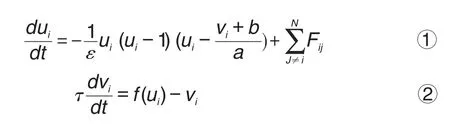
式中ui和vi分别为描述神经元状态的膜电位和恢复电流，τ为时间常数，N为神经元数目。F为神经元之间的连接关系。图1A中u（t）和v（t）随时间的变化模拟了单个神经元动作电位产生过程。

除了无标度拓扑结构这一特性，为了避免神经网络出现爆炸性发放活动，该模型的另一重要特性在于枢纽神经元被激活的难度比低连接度神经元更大。该特性有2种不同的实现方式：一种是考虑2个神经元之间的电突触耦合［15］。令Fij=C0Jij（ujui），若神经元i和j之间存在连接，则权重Jij=Jji=1，否则Jij=Jji=0。电突触耦合可被等效看作是2个神经元之间的连接电阻，具有平衡相邻2个神经元膜电位的功效。这一效应进而增加了枢纽神经元被激活的难度，这是因为枢纽神经元存在很多连接，其接受的兴奋性电流极易流到与其相连的神经元。通过选择合适的耦合强度C0，可使单个动作电位足以激活一个低连接度神经元（图1B），但若要激活一个枢纽神经元则需要2个或更多个动作电位的同时激发（图1C和1D）。

另外一种实现方式是传递效率随着突触连接度增多而降低的化学突触。令Fij=CiJijH（uj-θ），式中当uj＞θ时，H（uj-θ）=uj，其他情况下H（uj-θ）=0，表明神经元i只有在神经元j产生动作电位后才接受它的兴奋性输入。Jij=1意味着神经元i与j之间存在着化学突触连接，Jij=0则表示无化学突触连接。神经元之间的耦合强度会随着神经元的连接度数ki增加而降低，进而增加了神经元i被激活的难度。

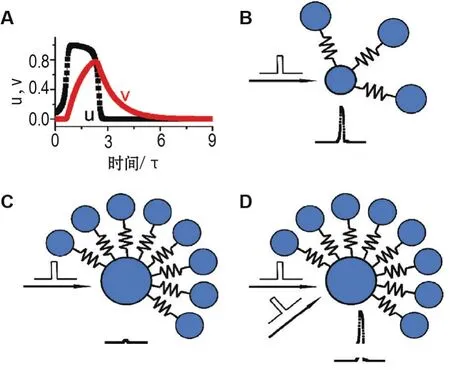
图1 神经元和神经突触的动力学特征［12］.A：单个神经元的动力学行为；当神经元产生动作电位后，进入不应期状态，最后恢复到静息状态.B：具有电突触连接的低连接度神经元示例。单个动作电位可激活低连接度神经元.C：具有电突触连接的枢纽神经元示例.单个动作电位不足以激活枢纽神经元.D：图1C中的枢纽神经元可被≥2个同时到达的动作电位激活.

2 无标度神经网络的神经活动及机制

2.1 无标度神经网络的周期同步发放行为

无标度神经网络模型具有维持长时程周期同步发放行为的能力。由电突触或化学突触耦合构成的神经网络所呈现的网络活动行为是类似的，所以，本文只以电突触连接的神经网络为例来进行说明。

图2A为一个随机生成的无标度神经网络，其中γ=3，神经元的数目N=210，神经元平均连接度数〈k〉=4。若从随机初始条件出发（ui和vi为0到1之间的均匀随机数），并根据式①和②来演化网络的活动状态，神经网络会有大约10%的概率演化到周期同步发放状态。

2.2 长时程周期同步发放的神经网络内在机制

为了揭示网络活动状态的内在机制，本课题组详细研究了周期同步发放状态下所有神经元的活动行为，发现大多数神经元在一个周期活动中只发放一次（图2C），该类神经元被定义为T1神经元；少数神经元在一个周期内可以发放2次（图2D），定义为T2神经元。进一步研究发现，正是这种不同的神经元活动模式揭示了网络动力学的内在机制。对网络中所有神经元的位置进行重新排列，将T2神经元置于中间，得到图2E。从图2E中可发现，所有的T2神经元都是低连接度神经元，而且这些低连接度的神经元形成一个环状结构。

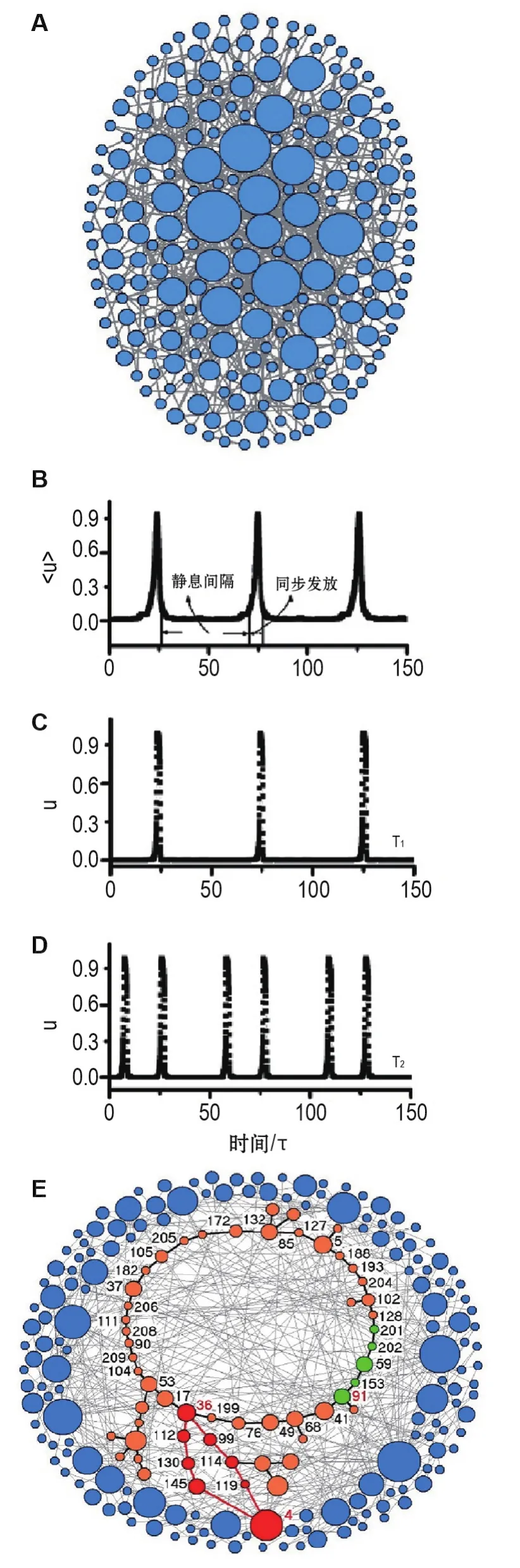
图2 无标度神经网络的动力学行为［12］.A：无标度神经网络示意图，图中神经元直径与其连接度成正比.B：神经网络活动状态呈现出一长时程周期性同步发放行为.C：T1神经元在单个周期内只发放一次.D：T2神经元在单个周期内发放两次.E：重置图2A中所有神经元的位置：将T2神经元（绿色和橙色）置于中间位置，其余神经元置于外周.所有T2神经元都是低连接度神经元，并构成一个环.图中红色路径表示低连接度环中的神经信号沿该路径传递到枢纽神经元.

网络动力学变化的过程可被清晰地揭示：假设编号为91的神经元（图2E中标记为红色的神经元）最先被激活，该神经活动信号会沿着低连接度神经元所组成的环逆时针方向传播。一开始，低连接度环上的神经信号不足以诱发网络的同步发放，网络仍处于静息状态。只有当信号传递到编号为36的神经元时，网络的同步发放行为可被诱发，这是因为36号神经元可同时激发多条传播路径（图2E中的红色路径），进而激活编号为4的枢纽神经元；枢纽神经元可通过其丰富的连接度诱发网络中剩余神经元的发放。同步发放之后，网络活动状态恢复到静息状态，这是由于大多数神经元在此时都处于不应期（refractory period）。

因此，无标度神经网络可产生长时程周期同步发放活动的工作原理如下：①网络中的枢纽神经元透过高连接度触发整个网络的同步发放；②大量低连接度神经元构成的环在网络同步发放的间隔阶段维持了网络的活动，该低连接度环的长度决定了同步发放的周期，即可记录时间节律信息；③电突触或强度随神经元连接度减小的化学突触减小了枢纽神经元的发放概率，从而避免网络的癫痫式振荡。

3 无标度神经网络的“库网络”特性

无标度神经网络模型具有维持较大范围内的节律性活动的能力。对具有300个神经元的无标度神经网络中低连接度环的长度分布进行统计发现（图3A），该分布较宽泛，这表明无标度神经网络将像一个资源丰富的“库”。网络所能存储的最长节律由网络中最长的低连接度环（记为Lmax）来决定。

进一步统计Lmax与网络尺度N的关系（图3B），其线性拟合结果为Lmax≈0.12N+0.8。因此，当网络尺寸在104～105量级（斑马鱼视顶盖神经环路中神经元数目的一个粗略估计）时，Lmax则在1.2×103～1.2×104的范围内；同时考虑到单个神经元的时间常数大约在10 ms的量级和神经元之间信号传递的时间延迟大约为1 ms，神经信号沿着Lmax传播所消耗的时间范围为13～130 s。以上结果表明，该研究所构建的无标度神经网络模型可实现实验中所观测到的对20 s时间节律信息的记忆。

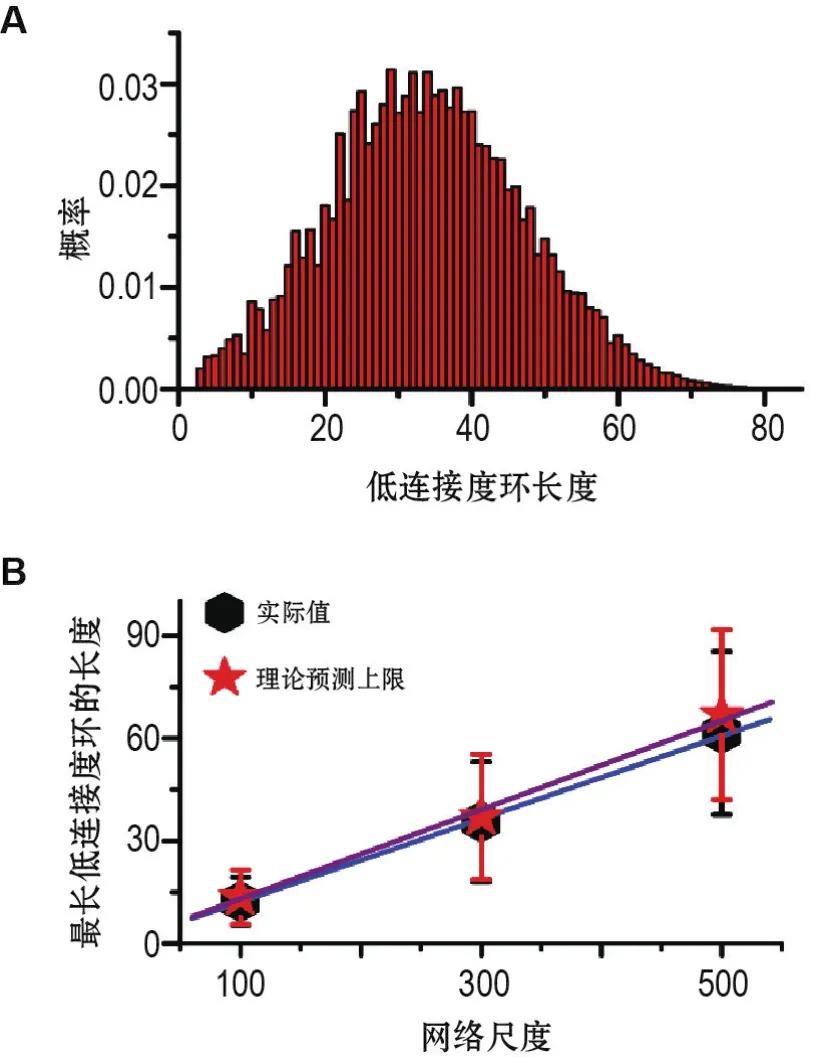
图3 无标度神经网络的“库网络”特性［12］.A：具有300个神经元的无标度网络中低连接度环的长度统计分布，图示结果为随机生成的100个无标度网络的平均值；B：低连接度环的最大长度与网络尺度的关系，每个数据点均为随机生成的100个无标度网络的平均结果.

4 时间节律信息的提取机制

上述研究表明，若要在网络中维持长时程周期性同步发放活动，关键是需要一个长度合适的低连接度环，以及连接在该环上的、可被该环激活的枢纽神经元。但神经系统如何根据外部周期性输入获得这一必要的网络结构？神经系统可通过学习过程习得。

采用生物学所广泛使用的Hebbian学习律来实现这个功能［15-17］，其基本思想是：网络中丰富的环或链结构能长时间地保持输入的残余活动信息，当外部输入不断节律性地呈现时，网络中与输入节律相吻合的环或链就通过Hebbian学习律得到了加强，被这种学习“挑选”出来，协助网络维持了与输入相同节律的同步发放，实现对输入时间信息的提取和再现。

具体过程如下：在t=0时刻，刺激首先呈现给了网络中随机选择出的4%的神经元（记为神经元群A），该群神经元会被瞬间激活，网络产生同步发放。同步发放后，神经网络活动会沿着不同的路径在网络中传播，从而能有效地保留外部刺激的记忆轨迹（图4A），这为联想记忆学习提供了重要的基石。在t=T时刻，残余的神经网络活动传播到神经元群B，同时新一轮的刺激会到达神经元群A。根据Hebbian学习法则，在每个刺激呈现的时间窗口内，神经元群A和B之间的突触连接不断增强，直至形成一个长度为T的闭环连接。另外，外界刺激诱发了网络的同步发放，这意味着神经元群A中包含了枢纽神经元，并且枢纽神经元在学习之后也被牢牢地连接在低连接度环上。经过上述学习过程，神经网络就产生了与外部刺激节律相匹配的周期同步发放行为（图4B）。

图4 时间节律信息的提取机制［12］.A：随机刺激无标度神经网络中4%的神经元，网络会产生同步发放活动，同步发放之后，网络能维持长时间的刺激的记忆痕迹；B：刺激重复呈现20次之后，网络通过Hebbian学习法则可产生周期性同步化发放.

5 结语和展望

本文介绍了一个简单、有效的机制来产生并维持神经系统中的长时程周期性同步发放。该网络模型具有无标度特殊拓扑结构，并包含丰富的具有不同尺寸的低连接度环，这一特性保证了神经系统具有处理不同时间范围的周期性输入信息的能力。当周期性呈现一个外部输入，网络就通过简单的Hebbian学习律从资源库里选出和输入节律相吻合的环。

无标度的网络结构和枢纽神经元难以被激活的特性是该网络模型的重要特性。严格来讲，网络结构不必完全满足无标度特性，只需使得网络中包含少数的枢纽神经元和大量的低连接度神经元。这种连接方式可很好地在信号通讯的有效性和网络连接的经济性之间获得平衡。大量的实验研究也证明了神经系统的确具有无标度拓扑结构。如发育过程中小鼠海马区的神经网络结构［18］和基于功能性磁共振成像数据得到的大脑功能连接网络的拓扑结构都具有无标度特性［19］。另外，还有实验数据显示，刺激单个或少量皮质神经元能显著影响直觉和运动输出［20］，以及大脑的整体状态［21］，这极大地表明了枢纽神经元存在的可能性。最新实验数据揭示，无标度拓扑结构极有可能广泛存在于大脑皮质的层状结构中，即层（Layer）2/3是枢纽神经元，而Layer5是低连接度神经元。本课题组的工作揭示，这种特殊拓扑结构在神经计算中具有至关重要的作用，极有可能是神经环路处理时间域信息的基本架构。

为了实现枢纽神经元难以被激活的特性，采取了2种可行机制。一是神经元之间的电突触连接。实验数据已证实，电突触连接大量地存在于视网膜的神经节细胞和皮质的中间神经元。电突触是否也存在于某些皮质的兴奋性神经元之间的连接中还未可知。另外一种机制是随突触后神经元连接度增加而降低的化学突触连接。化学突触连接强度如是均匀的，枢纽神经元会诱发高频振荡，从而使得无标度网络不能维持长时程周期性同步发放。化学突触连接强度与神经元连接度的平方根成反比，长时程周期节律则能很好地被保留下来。值得注意的是，这一条件也是兴奋-抑制平衡网络产生不规则网络活动的条件。同时，也有实验数据表明，突触的传递效率随突触后神经元的连接度增加而降低［22］。

一般来讲，若是一个网络具有无标度拓扑结构（即网络中具有少数枢纽神经元和大量低连接度神经元）和枢纽神经元难以被激活的特性，那么该网络即可实现前述的所有动力学行为。其他动力学系统是否也存在这些特性有待于进一步研究。

一般认为，同步振荡在大脑功能实现上起到了重要作用。已有研究提出不同的机制来产生神经元响应中的节律行为，如从单个神经元的性质（即振荡器特性）到神经元的群体动力学等。这些已有机制的一个重要挑战是：如何协调网络的规则振荡和单个神经元的不规则响应之间的矛盾。本文所介绍的模型产生长时程周期振荡的机制在于神经活动是沿着低连接度环进行传播的，因此这一机制与单个神经元对恒定刺激的不规则响应之间并不存在矛盾。

本课题组所提出的机制对研究神经信息处理具有深远的影响。神经系统能利用其内在的低连接度神经元形成的环来存储外部输入信息的记忆痕迹，由此可作为处理时序信息的基石。另外，该模型与库网络的理念相一致［23］。

针对领域内长期争论的焦点，本课题组的工作支持局域神经环路可利用其内在网络动力学特性来分布式地处理时间这一观点，同时也回答了领域内一个极具挑战性的理论难题，即如何维持长时程周期性同步发放行为。

［1 ］Kandel E，Schwartz J，Jessell T，Siegebaum S，Hudspeth A.Principles of Neural Science（神经科学原理）［M］.Fifth Edition.New York：McGraw-Hill Ryerson.2013：330-350.

［2 ］Carr CE.Processing of temporal information in the brain［J］.Annu Rev Neurosci，1993，16：223-243.

［3 ］Mauk MD，Buonomano DV.The neural basis of temporal processing ［J］.Annu Rev Neurosci，2004，27：307-340.

［4 ］Buhusi CV，Meck WH.What makes us tick？Functional and neural mechanisms of interval timing［J］.Nat Rev Neurosci，2005，6（10）：755-765.

［5 ］Ivry RB，Schlerf JE.Dedicated and intrinsic models of time perception［J］.Trends Cogn Sci，2008，12（7）：273-280.

［6 ］Hopfield JJ.Neurons with graded response have collective computational properties like those of two-state neurons［J］.Proc Natl Acad Sci USA，1984，81（10）：3088-3092.

［7 ］Fuster JM，Alexander GE.Neuron activity related to short-term memory［J］.Science，1971，173（3997）：652-654.

［8 ］Gibbon J.Scalar expectancy theory and Weber′s law in animal timing［J］.Psychol Rev，1977，84（3）：279-325.

［9 ］Karmarkar UR，Buonomano DV.Timing in the absence of clocks：encoding time in neural network states［J］.Neuron，2007，53（3）：427-438.

［10 ］Buonomano DV，Maass W.State-dependent computations：spatiotemporal processing in cortical networks［J］.Nat Rev Neurosci，2009，10（2）：113-125.

［11 ］Sumbre G，Muto A，Baier H，Poo MM.Entrained rhythmic activities of neuronal ensembles as perceptual memory of time interval［J］.Nature，2008，456（7218）：102-106.

［12 ］Mi Y，Liao X，Huang X，Zhang L，Gu W，Hu G，et al.Long-period rhythmic synchronous firing in a scale-free network［J］.Proc Natl Acad Sci USA，2013，110（50）：E4931-E4936.

［13 ］Barabasi AL，Albert R.Emergence of scaling in random networks［J］.Science，1999，286（5439）：509-512.

［14 ］Bär M，Eiswirth M.Turbulence due to spiral breakup in a continuous excitable medium［J］.Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics，1993，48（3）：R1635-R1637.

［15 ］Bi GQ，Poo MM.Synaptic modifications in cultured hippocampal neurons：dependence on spike timing，synaptic strength，and postsynaptic cell type［J］.J Neurosci，1998，18（24）：10464-10472.

［16 ］Bloomfield SA，Völgyi B.The diverse functional roles and regulation of neuronal gap junctions in the retina［J］.Nat Rev Neurosci，2009，10（7）：495-506.

［17 ］Yang XD，Korn H，Faber DS.Long-term potentiation of electrotonic coupling at mixed synapses［J］.Nature，1990，348（6301）：542-545.

［18 ］Bonifazi P，Goldin M，Picardo MA，Jorquera I，Cattani A，Bianconi G，et al.GABAergic hub neurons orchestrate synchrony in developing hippocampal networks［J］.Science，2009，326（5958）：1419-1424.

［19 ］Eguíluz VM，Chialvo DR，Cecchi GA，Baliki M，Apkarian AV.Scale-free brain functional networks［J］.Phys Rev Lett.2005，94（1）：018102.

［20 ］Brecht M，Schneider M，Sakmann B，Margrie TW.Whisker movements evoked by stimulation of single pyramidal cells in rat motor cortex［J］.Nature，2004，427（6976）：704-710.

［21 ］Morgan RJ，Soltesz I.Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures［J］.Proc Natl Acad Sci USA，2008，105（16）：6179-6184.

［22 ］Li H，Li Y，Lei Z，Wang K，Guo A.Transformation of odor selectivity from projection neurons to single mushroom body neurons mapped with dual-color calcium imaging［J］.Proc Natl Acad Sci USA，2013，110（29）：12084-12089.

［23］Jaeger H，Maass W，Principe J.Special issue on echo state networks and liquid state machines［J］.Neural Networks，2007，20（3）：287-289.