风险项目投资组合决策的贝叶斯评价与选择策略

胡支军，彭 飞，李志霞

(1. 贵州大学数学与统计学院，贵州 贵阳 550025；2. 贵州省公共大数据重点实验室，贵州 贵阳 550025；3. 华南师范大学经济管理学院，广东 广州 510631)

风险项目投资组合决策的贝叶斯评价与选择策略

胡支军1,2，彭 飞3，李志霞1

(1. 贵州大学数学与统计学院，贵州 贵阳 550025；2. 贵州省公共大数据重点实验室，贵州 贵阳 550025；3. 华南师范大学经济管理学院，广东 广州 510631)

项目投资组合选择是许多风险投资公司的重要决策问题，风险投资公司利用有限的资源通过选择和执行项目组合试图创造价值，而风险投资家的行为偏好直接影响最优项目组合选择的结果。通常，风险项目的价值是不确定的，因此风险投资家必须基于对风险项目未来价值的事前估计进行投资决策。在展望理论框架下，构建了考虑风险投资家损失厌恶心理特征的风险项目投资组合优化模型，给出了处理项目组合选择中价值估计不确定性的贝叶斯方法，并应用Monte Carlo模拟将模型转化为线性整数规划问题。研究发现，相对于直接基于事前价值估计的投资组合选择，对项目价值事前估计不确定性的贝叶斯建模可以给出更加精确的价值估计，并使用所获得的修正估计进行投资组合决策，可以帮助选择具有更高的事后期望效用的项目组合，消除估计的事前期望效用与事后实现的期望效用之间的预期间隔，降低风险投资家预期的决策后失望程度。

项目投资组合；损失厌恶；贝叶斯建模；决策分析

1 引言

随着经济全球化与市场竞争的激烈化，风险项目投资组合愈来愈成为理论和实践关注的热点问题，科学地做出风险资本的投资组合决策对提高风险投资机构的投资效率乃至加速我国风险投资业的发展具有重要的战略意义。在现实的经济活动当中，为使投资风险最小或投资回报最大，风险投资机构通常会对不同领域、不同性质的项目进行组合投资，其目的在于规避项目运行中的系统风险或获取较高的投资回报率。如果项目选择不当就会阻碍个人或组织的发展，甚至带来灾难性的损失。因此，对于风险投资公司(或风险投资家)来说如何有效的分配有限的资源，通过选择和执行项目投资组合，获得最大的投资收益就显得非常重要。

通常情况下，某些项目被选择是基于对它们事后(Ex post)将提供多少价值的事前(Ex ante)估计而进行的。关于风险项目的未来价值的估计可以通过例如净现值计算、内部收益率法(IRR)、成本-效益研究或多属性决策分析等方法获得[1-2]。然而，在必须做出投资决策的时刻，项目的真实价值是未知的，只能获得某个预测。显然，预测值越高的项目越有可能被选择。在实际投资过程中，风险项目通常由于关联或依赖于某些不确定的未来事件而使得其未来价值具有不确定性，而风险投资家必须在给定的资源和其他相关约束下,基于对风险项目未来价值的事前估计做出投资决策。为了降低不确定性并改进决策过程，风险投资家会设法从各种渠道获得关于项目未来价值的预测，例如通过咨询掌握数据的专家，并可以根据某个经验模型获得一个后验估计值。由于这些估计通常是不确定的，对项目未来价值的预测会有随机误差，因此风险投资家实际上难以在满足相关的预算和其他资源约束下选择具有最高的事后价值总和的项目组合。特别地，即使事前的价值估计是无偏的，而最终所选择的项目组合所实现的事后价值通常可能会低于其所包含的那些项目的事前估计值，也即所选择的投资组合很有可能是事后次优的。换句话说，在投资期末，项目的真实价值实现时，风险投资家可能会遭受所谓的决策后的失望(Post-decision disappointment)[3-4]。

现有的关于多项目投资组合的研究主要是在均值-风险模型框架下开展的。例如，Zhang Qun等[5]讨论了当无法获取历史数据时，基于专家对项目年度现金流入与流出和初始投资支出的评价的资本预算问题，建立了最优项目选择的一个均值-风险指数模型。Hall等[6]讨论了当仅具有每个项目的不确定收益的部分概率分布信息时的项目选择问题，决策者选择备选项目组合的一个可行子集使得投资组合收益不能达到某个给定目标的风险最小化。徐维军等[7]在可信性测度下，建立了具有破产风险约束的多项目投资组合优化模型。于超与樊治平[8]则提出了一种涉及多个行业的考虑决策者后悔厌恶的风险投资项目选择方法。

在金融优化领域，对资产收益不确定性的贝叶斯(Bayesian)建模研究已有较长的历史[1, 9]。特别地，作为对最近的市场信息的反应，Bayesian分析被用于修正模型参数，以更好地预测证券价格，并进一步帮助投资者做出最优证券投资组合决策[10]。然而，证券投资组合优化与项目投资组合选择在许多方面是不同的。首先，风险项目没有可以从市场中观察的市场价格，而且，项目的价值通常由专家的评价进行估计。其次，项目投资的决策变量为二元0-1变量，即要么选择要么拒绝[11]，而证券投资组合本质上可以对任意的证券投资小数数量的资金。最后，尽管不同证券的价格可能是相关的，但大多数情况下对证券的投资并没有逻辑上的相互依赖性。但是在项目投资组合中，由于逻辑关系，项目之间可能会有多种形式的相互依赖性。例如，某两个项目可能是相互排斥(项目A和B只能选择其一)的或相互依赖的(如果项目B是项目A的后继项目，则只有当A被选择时才能选择B)。由于上述这些差异，在项目投资组合选择中更需要对估计的不确定性做出精细的分析。

最近，Vilkkumaa等[12]证明了，与基于事前价值估计的直接投资组合选择相比较而言，对风险项目价值估计的不确定性进行Bayesian建模并将所获得的Bayes修正估计应用于投资组合选择可以：(1) 帮助选择可能预期提供更高事后价值的项目投资组合；(2)消除实现的事后投资组合价值与估计的事前投资组合价值之间的预期间隔(Gap)，从而降低决策者可能会经历的失望的程度。但是，Vilkkumaa等[12]的研究假定决策者是风险中性的，决策目标是最大化项目投资组合的期望价值，对具有内在价值不确定性的项目组合进行比较时并没有考虑决策者的风险态度。行为金融学研究表明，风险投资家对项目投资组合的风险偏好通常会影响投资绩效和决策行为。

传统的Von-Neumann期望效用理论认为投资者是对同等数量的收益和损失的心理感受是一样的,风险厌恶型投资者的决策目标是最大化期末财富的期望效用。Kahneman与Tversky[13]提出的展望理论(Prospect theory)则发现投资者在做投资决策时，关注的是期末财富相对于某个给定的参照点的变化，即盈利或损失，投资者对于相同规模的盈利和损失的心理反应是不一样的，对损失更加敏感，即投资者是损失规避的。近年来，在损失厌恶框架下讨论投资组合问题引起了许多研究者的兴趣[14]。例如，Fulga[15]在均值-风险框架下给出了考虑投资者损失厌恶偏好的投资组合优化问题。金秀与王佳等[16,17]研究了动态损失厌恶投资组合模型的最优资产配置和绩效表现。张茂军等[18]从风险约束的视角研究了基金管理者呈损失厌恶的投资决策问题。 然而，现有的基于损失厌恶的投资组合研究主要局限于证券市场，对于其它资产类型(例如房地产、不动产以及一般的项目投资)的相关研究还极为少见。

由于根据历史数据或专家评估对风险环境下项目的未来价值所作出的预测通常与项目最终实现的价值具有较大的差异，本文在文献[3,4,12]研究的基础上， 将风险投资家的损失厌恶心理引入项目投资组合选择过程，构建了基于风险投资家损失规避心理特征的风险项目组合投资优化模型，并采用Bayes方法对项目真实价值的事前估计进行修正；进一步，本文提出了求解优化模型的Monte Carlo方法，该方法通过模拟项目的未来价值，可以克服在某些场合下样本数据可能不足的缺陷。理论分析与模拟计算表明：(1)与Simith等[3],Chen和Dyer[4]和Vilkkumaa等[12]的基于风险中性的投资组合模型不同的是，本文发现风险投资家的损失规避行为对其投资组合策略具有重要的影响；(2)对风险项目价值估计的不确定性进行显式的Bayesian建模并将所获得的Bayes修正估计应用于投资组合选择，可以帮助风险投资家选择可能预期提供更高的事后效用值的项目组合，降低风险投资家的决策后的失望程度，从而可以更有效地选择项目组合。本文的研究结果可以为风险投资家的投资组合决策提供一定的理论依据和方法。

2 风险环境下的项目投资决策模型

考虑1,…，m个备选项目集合，风险投资家的目标是从这些项目集中选择一个子集，在满足相关的约束下，最大化所选择的项目组合的期望效用值。例如，投资的总成本不能超过给定的预算阈值。其它可能的约束包括项目间的相互排斥(例如，只有当项目B没有被选择时才能选择项目A，反之亦然)，或项目间的逻辑依赖性(例如，仅当项目B被选择时，才能选择项目A)。这个投资组合选择可表示为具有0-1元素的决策向量z=[z1,…，zm]，使得只有当项目i被选择时zi=1。

项目的真实价值为v=[v1,…，vm]T，这些价值是随机变量V=[V1,…，Vm]T～f(v)的实现值，仅当在投资期末这些项目被执行后，它们才会被实现和观测到。在下文中，假设分布f(v)是已知的。

具有损失厌恶风险偏好的风险投资家的效用函数定义为下面的分段线性函数[14]：

(1)

其中λ>1为损失厌恶系数，X表示投资组合的期末价值，V0是盈利和损失的参照点。(1)式表明，在参照点附近，损失的斜率大于盈利的斜率，即风险投资家对一定数量的损失比对相同数量的盈利更加敏感，λ越大意味着对损失的厌恶程度越高。

用Z表示所有满足给定约束的可行投资组合构成的集合，在进行投资决策的时刻，如果风险投资家可以观察到项目的真实价值v，则其最优投资组合z(v)将通过求解下面的优化问题而确定：

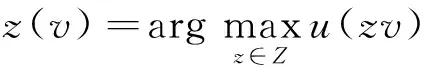
(2)

其中u(·)为风险投资家的由(1)式定义的损失厌恶效用函数。

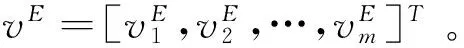
(3)

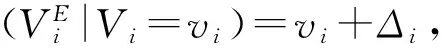
首先，利用Matlab软件，由Vi～N(10,42)生成项目P7,…,P12真实价值的一组实现值vi分别为9.62,6.67,11.18,4.66,12.86,16.49,7.65,18.73,9.45,10.46,14.27,10.24，则根据模型(2)，可求得最优投资组合z(v)是选择{P3,P5,P6,P8,P11}，其所实现的项目总效用值u(z(v)v)为23.53。

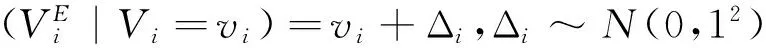
从这个例子可以发现，(a)基于估计值vE的投资组合z(vE)所实现的事后项目总效用值(20.19)低于最优投资组合z(v)所实现的总效用值(23.53);(b) 投资组合z(vE)包含了“激进型”项目P10和P12，这两个项目由于具有较高的估计值而被选取，但它们没有被最优投资组合z(v)选取；(c)投资组合z(vE)的事前总价值估计为(87.57)，比其实际所实现的事后总价值(70.19)高24.8%, 从而决策者将经历决策后的失望。

正式地，本文给出了下面的定理1，其详细的证明过程参见附录。

定理1 设VE是V的一个条件无偏估计，则:

E[u(z(VE)V)-u(z(VE)VE)]≤0

其中，z(VE)是问题(3)的最优解。进一步，设z(V)是问题(2)的最优解，若P(z(V)≠z(VE))>0，则有E[u(z(VE)V)-u(z(VE)VE)]<0。

定理1表明，在平均的意义下，投资组合z(VE)事后实际所实现的项目总效用值不会超过其事前估计的效用值。而且，如果选择“错误的”项目(除非估计是完全精确的，否则总是会这样)的概率大于零，则基于事前估计值所选择的项目组合在投资期末实际所实现的效用值u(z(VE)V)，与该项目组合的估计的效用值u(z(VE)VE)之间的预期间隔是严格小于零的。特别地，即使对项目真实价值的估计是无偏的，由于那些价值被高估的项目更有可能被选择，从而使得事后所选择的投资组合的效用值也会被系统地高估，导致风险投资家将经历决策后的失望。而且，对项目真实价值的事前估计的不确定性越高，在投资期末预期的失望也就越大。

3 项目投资组合中不确定性的贝叶斯建模

Smith等[3-4,12]的研究发现，与从多个备选方案中只选择一个方案的问题类似，对风险环境下的项目投资组合选择问题，投资者决策后的失望可以通过应用Bayesian建模对项目价值的事前估计值进行修正而得到减轻。

具体地，给定项目的估计值VE，可以应用Bayes法则f(v|vE)∝f(v)f(vE|v)从先验分布f(v)和似然分布f(vE|v)获得项目价值v的后验分布f(v|vE)。进一步，给定估计值vE，可以应用后验分布f(v|vE)计算项目i的期望值E[Vi]VE=vE] 或项目i属于最优投资组合的概率P(zi(V)=1|VE=vE)。从而，后验分布可以用于构建投资组合优化问题，目标是最大化项目组合价值的期望效用。

给定vE，投资者的决策问题是选择投资组合z，最大化损失厌恶效用函数u(zE[V|VE=vE])。因此，根据项目的事前估计值vE，可通过下面的式子:

(4)

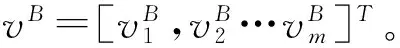
基于Bayes估计值vB，最大化风险投资家期望效用的投资组合可由下面的优化问题确定:

(5)

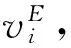
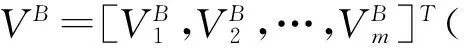
(6)

本文指出，在相当一般的假设下，基于Bayes估计vB的投资组合所实现的事后效用值，将与直接基于事前估计值vE的投资组合所实现的事后效用值至少一样多。正式地，本文证明了下面的定理2。

定理2 设VE,V及z(VE)的含义如定理1中所示，则有:

E[u(z(VE)V)-u(z(VB)V)]≤0

其中，VB由(6)式给出，z(VB)是模型(5)的最优解。进一步，若z(vE)≠z(vB)发生的概率大于0，则有E[u(z(vE)V)-u(z(vB)V)]<0.且:

E[u(z(VE)V)-u(z(VB)V)]<0

这是一个直观的结果，因为根据模型(5)，z(vB)最大化投资组合的期望效用。而且，如果使用Bayes估计vB有非零的概率导致与直接使用估计值vB选择不同的投资组合，则基于Bayes估计的投资组合z(vB)将会获得严格更高的效用。

一般情况下，项目价值的后验分布没有封闭的表达式。但是，如果考虑项目的真实价值和估计值的分布是共轭分布的情形，则可以获得Bayes估计的一个封闭的解析表达式[3,12]。例如，假定项目的真实价值与估计值服从自共轭正态分布，使得对每个项目i有:

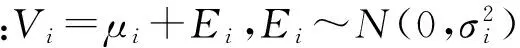
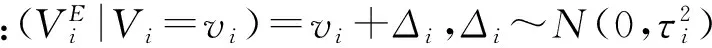
从而,(4)式的Bayes估计变为:

(7)

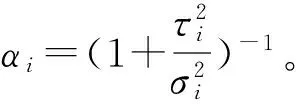
在某些场合，先验分布f(v)可能不是正态的。例如，项目价值可能是非对称分布的，其概率分布的大部分数据点集中于较小的值。对这种情形，一种可能的先验分布是非对称三角分布[20]，它仅需估计vi的三个参数，即最大值、最小值以及最可能值(众数)。此外，风险投资家也可以估计每个项目i的价值vi的百分位数，然后通过应用核光滑方法[21]将所导致的阶梯函数转换为连续分布函数。

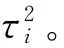
可以证明，实际上不需要对先验分布f(v)和似然分布f(vE|v)或者问题的相关约束作出任何特定的假设(例如，正态分布)，Bayes估计可以消除所选择的投资组合实现的事后期望效用值与估计的期望效用值之间的预期间隔。正式地，本文给出下面的定理3。

定理3 设V,VE,VB及z(·)的含义如定理2中所示，则下式

E|u(z(vB)V)-u(z(vB)vB)|VE=vE]=0

对所有的vE成立，而且有

E|u(z(VB)V)-u(z(VB)VB)]=0.

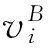
在实际应用中，如果先验分布和似然分布是共轭的，则应用Bayesian法则可以获得每个项目i的后验分布的解析表达式[19]。如果先验分布和似然分布不是共轭的，则需要对后验分布进行近似。这可以通过以下方式实现[12]，首先，从先验分布f(v)抽取L个样本值vi(l)(l=1,…,L)对Vi的分布离散化，然后，对应于每个vi(l),从VE|Vi=vi(l))的似然分布抽取K个样本值vE(l,k),k=1,…,K。从而，即可通过在离散联合分布中令VE=vE并标准化所导致的边际分布函数，获得相应于初始估计vE的后验分布。如果离散化足够稠密，则对备选项目的价值独立分布的问题，这种方法运行效果良好。但如果备选项目之间的价值与估计值都具有依赖性，在一个稠密的多维网格的每一个点抽取充分大数量的数据可能需要付出相当高的计算努力，此时可以应用韦来生等[19]和Ruppert等[23]给出的模拟和数值积分策略。

4 基于损失厌恶的风险投资组合优化模型

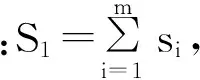
进一步假设，投资于风险项目i可以获得的收益(价值)为Vi，因此，考虑风险投资家损失厌恶心理特征的项目投资组合优化模型可描述为:

(8)

其中，效用函数u(·)为由模型(1)所定义的分段线性函数。

由于通常难以获得模型(8)中目标函数的解析表达式，可以考虑采用MonteCarlo模拟方法进行求解[18,24]。 该方法的基本思想是根据随机变量的分布函数、均值和方差等统计特征，利用随机数生成算法，产生表示项目收益率的随机数，将原问题(8)转化为确定性的优化问题，然后再应用确定性优化问题的求解算法求出原问题的近似解。下面给出问题(8)的具体求解过程。

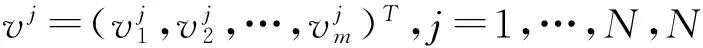
(9)

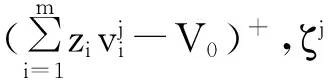
Xj-V0=(Xj-V0)+-(Xj-V0)-

可将模型(8)转化为下面的线性混合整数规划问题：

(10)

此外，为了考察风险投资家的损失厌恶行为对投资组合决策的影响，我们还求解如下的最大化项目组合总期望价值的投资组合优化模型[12]:

(11)

根据模型(10)和(11)，若风险投资家的投资目标是项目组合的预期总价值，则期末投资组合的期望值为E(zV)，而当风险投资家为损失厌恶时，投资组合的目标函数是E(zV-V0)+-λE(zV-V0)-。比较这两个目标函数可知，在具有相同的预算约束下，风险投资家的损失厌恶系数λ是导致模型(10)和模型(11)的目标不相同的关键因素。也即模型(8)中的目标函数反映了当风险投资家面临一定数量的损失时所承受的痛苦要大于相同数量的盈利所带来的快乐。因此，本文建立的模型体现了风险投资家的损失厌恶心理特征，而文献[12]的模型以项目投资组合的期望值为目标则反映了风险投资家在做决策时是风险中性的。

5 数值算例

5.1 损失厌恶对投资组合选择的影响分析

为了检验损失厌恶型风险项目投资组合优化模型(10)以及对项目价值估计不确定性的Bayesian建模在实际应用中的有效性，本文应用Monte Carlo随机模拟产生备选项目的价值数据，并分别计算模型(10)和模型(11)的最优投资组合方案。

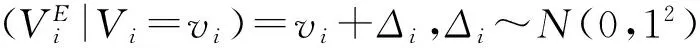
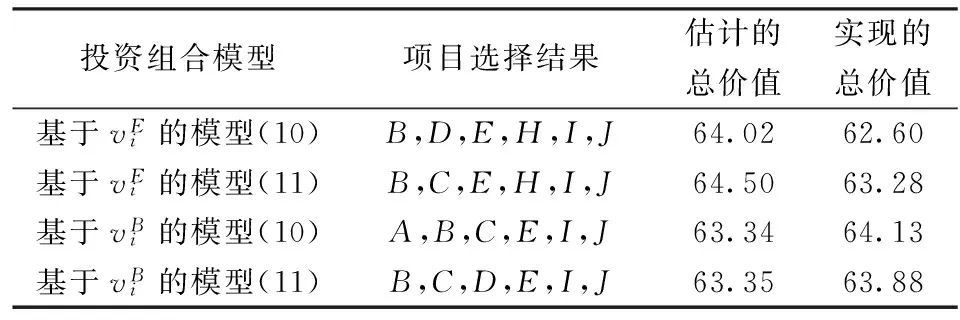
表1 损失厌恶行为对投资组合的影响

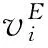
5.2 项目估计的不确定性对投资组合选择的影响分析

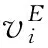
下面的图1给出了当估计误差的标准差τ变化时，运行Monte Carlo模拟1000次，求解模型(10)获得的投资组合所估计的平均效用值Eu(z(VE)VE及其所实现的事后平均效用值Eu(z(VE)V的变化情况。从图1不难看出，随着项目价值的估计误差δi的标准差τ的增大，决策后的失望程度也增大。也就是说，项目价值事前估计的不确定性越大，不仅使得风险投资家难以识别那些具有高真实价值的项目，而且也使得风险投资家更可能会选择那些具有高的估计值的项目，从而预期的失望也就越大，这也就通过数值模拟检验了定理1的合理性。例如，在图1中，当τ=0.8时，所选择的投资组合估计的平均效用值为22.22，比其所实现的事后平均效用值13.53要高64.23%。

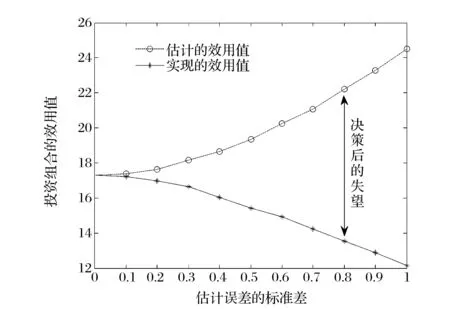
图1 估计误差的标准差增大时模型(10)的投资组合对应的期望效用估计值与实现值

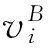
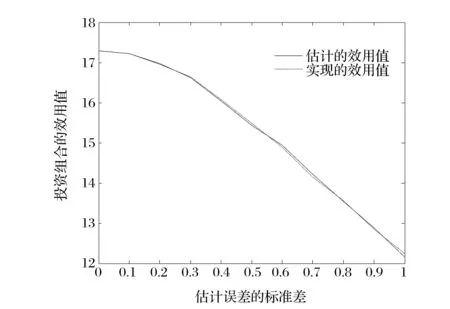
图2 基于Bayes估计值的投资组合所估计的期望效用值与实现的期望效用值

5.3 Bayes建模对投资组合业绩的影响分析

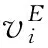
图3 分别基于直接估计值与基于Bayes估计值的投资组合的业绩表现

6 结语

传统的投资组合问题以Von-Neumann期望效用理论为基础，大量的实证研究发现，投资者在做投资决策时会偏离期望效用理论，不一定完全厌恶风险，而经常表现出诸如损失厌恶、框架依赖、过度自信等非理性行为。行为决策理论的研究使得人们认识到，投资者的行为偏好对资产配置起着重要的作用。本文从行为金融学的角度考虑风险投资家的损失厌恶偏好，在Vilkkumaa等[12]研究的基础上，构建了基于损失规避决策行为的风险项目投资组合优化模型。考虑到对风险项目未来价值估计的不确定性，应用Bayesian建模对风险项目的事前价值估计进行修正，研究发现Bayes修正估计倾向于给出更加精确的项目价值估计。同时，利用Monte Carlo随机模拟算法，将所构建的投资组合模型转化为容易求解的整数线性规划问题，对基于损失厌恶的投资组合模型与基于风险中性的投资组合模型进行了比较分析，发现风险投资家的损失规避心理对其投资决策具有重要的影响。此外，本文还从理论上证明了，对任意的先验分布和似然分布，与直接基于事前估计值的投资组合相比，对项目价值估计的不确定性进行Bayesian建模并将所获得的Bayes修正值用于构造投资组合，可以帮助风险投资家选择能够提供更高的事后效用值的投资组合，并减少其可能会经历的决策后失望，消除估计的事前效用值与实现的事后效用值之间的预期间隔。最后，通过Monte Carlo模拟检验了相关的理论结果。

需要指出的是，本文的分析基于假设项目价值的先验分布f(v)与似然分布f(vE|v)是已知的。由于项目投资组合对许多风险投资机构是一种经常性的活动，因此，可能会具有关于项目价值和价值估计的历史数据，从而可以利用这些历史数据对先验分布和似然分布进行估计[19,25]。但是，在风险投资实践中，某些风险项目通常没有或只有少量历史信息，如果风险投资家没有任何关于备选项目的先验信息，则此时可以应用仅基于评价信息的无信息先验方法来计算后验分布[26]。此外，如果先验分布和似然分布是共轭的，则可以应用Bayes定理获得每个项目i的后验分布f(vi|vE)的封闭表达式。但如果先验分布与似然分布不是共轭的，此时Bayes后验分布的确定需要计算高维积分。为了降低计算工作量,可以结合Markov链-Monte Carlo(MCMC)方法，对先验分布进行抽样，确定后验分布的离散值，通过离散值进行统计推断给出所求解的近似值[19,23]。

本文只考虑了单阶段投资决策问题，并且假设对每个项目的投资成本是确定的，但在实际投资活动中，风险投资公司为了规避风险可能会根据市场环境的变化而采用分阶段投资策略，项目的投资成本也可能会随时间而发生变化。因此，可以进一步研究同时考虑项目价值和成本的不确定性的多阶段投资组合问题。此外，在项目投资过程中还要面临背景风险，且背景风险与项目风险之间通常具有一定的相关性[27]，如何构建同时考虑背景风险和项目风险的多阶段项目投资决策模型也是值得深入研究的问题。

附录 ： 定理1的证明

【证明】对于给定的v和vE，有：

u(z(vE)v)-u(z(vE)vE)≤u(z(v)v)-u(z(vE)vE)

≤u(z(v)v)-u(z(v)vE)

(12)

其中，第一个不等式成立是因为z(v)是问题(2)的最优解，第二个不等式成立是因为z(vE)是问题(3)的最优解.因此，在V=v的条件下，随机变量VE的分布为f(vE|v)，对(12)式求期望可得：

E[u(z(vE)v)-u(z(VE)VE)VE)|V=v]

≤E[u(z(v)v)-u(z(v)VE)|V=v]

(13)

其中，最后一个等式成立是由于假设对项目价值的估计是条件无偏估计。由于对所有的v，(13)式都成立，因此有E[u(z(VE)V)-u(z(VE)VE)]≤0.

此外，如果有可能选择了非最优的项目，即P(z(V)≠z(VE))>0，则(12)式的第一个不等式对某些v和vE严格成立.因此，如果这个事件发生的概率为正，则对相应的v，不等式(13)严格成立，从而E[u(z(VE)V)-u(z(VE)VE)]<0.

定理2的证明

【证明】：对于给定的vE，则Bayes估计值vB，以及问题(3)和(5)的最优解z(vE)和z(vB)都是固定的，从而u(z(vE)V)-u(z(vB)V)的条件期望为：

E[u(z(vE)V)-u(z(vB)V)|VE=vE]

=u(z(vE)vB)-u(z(vB)vB)≤0

(14)

其中第二个等式是根据vB的定义，最后的不等式成立是因为z(vB)是问题(5)的最优解. 因此，对vE积分即可得E[u(z(VE)V)-u(z(vB)V)]≤0.

如果对某些vE，有z(vE)≠z(vB)成立，则对vB=E[V|VE=vE]，有：

u(z(vE)vB)-u(z(vB)vB)<0

因此，若P(z(VE)≠z(vB))>0，则不等式(14)严格成立，即：

E[u(z(VE)V)-u(z(vB)V)]<0

定理3的证明

【证明】：对给定的一组估计值vE，相应的Bayes估计值vB和问题(5)的最优解z(vB)也是固定的.对u(z(vB)V)-u(z(vB)vB)求条件期望可得：

E[u(z(vB)V)-u(z(vB)vB)]|VE=vE

由于vB是确定的，所以第一个等式成立，根据vB的定义，第二个等式也成立.对vE积分，即可得到E[u(z(VB)V)-u(z(VB)VB)]VB)]=0.

[1] Smidt S. A Bayesian analysis of project selection and of post audit evaluations[J].Journal of Finance，1979，34 (3)：675-688.

[2] Fliedner T，Liesiö J. Adjustable robustness for multi-attribute project portfolio selection[J]. European Journal of Operational Research，2016，252(3)：931-946.

[3] Smith J E，Winkler R L. The Optimizer’s Curse: Skepticism and postdecision surprise in decision analysis[J]. Management Science，2006，52(3)：311-322.

[4] Chen M， Dyer J. Inevitable disappointment in projects selected on the basis of forecasts[J]. SPE Journal，2009， 14(2)：216-221.

[5] Zhang Qun，Huang Xiaoxia，Zhang Chao. A mean-risk index model for uncertain capital budgeting[J]. Journal of the Operati-onal Research Society，2015，66(5)：761-770.

[6] Hall N G， Long Zhuoyu， Qi Jin， et al. Managing underperformance risk in project portfolio selection[J]. Operati-ons Research，2015，63(3)：660-675.

[7] 徐维军，罗伟强，张卫国．考虑破产风险约束的多项投资组合决策模型[J].运筹与管理,2013,22(6)：92-98.

[8] 于超，樊治平. 考虑决策者后悔规避的风险投资项目选择方法[J].中国管理科学，2016,24(6):29-37.

[9] Jacquier E，Polson N. Bayesian methods in finance[M]//Geweke J, Koop G, Van Dijk H.The Oxford handbook of Bayesian econometrics，Oxford,England: oxford university press,2011.

[10] Diris B，Palm F，Schotman P. Long-term strategic asset allocation: An out-of-sample evaluation[J]. Management Science. 2015，61(9)：2185-2202.

[11] 杨雷， 赵九茹.选择与评价新产品开发的风险决策研究[J]. 运筹与管理，2015，24(3): 127-133.

[12] Vilkkumaa E，Liesiö J，Salo A. Optimal strategies for selecting project portfolios using uncertain value estima-tes[J]. European Journal of Operational Research， 2014，233(3): 772-783.

[13] Kahneman D，Tversky A. Prospect theory: An analysis of decision under risk[J].Econometrica, 1979, 47(2): 263-291.

[14] Barberis N，Huang Ming，Santos T. Prospect theory and asset prices[J].The Quarterly Journal of Economics，2001，116 (1):1-53.

[15] Fulga C. Portfolio optimization under loss aversion[J]. European Journal of Operational Research，2016，251(1): 310-322.

[16] 金秀，王佳，高莹． 基于动态损失厌恶投资组合模型的最优资产配置与实证研究[J]. 中国管理科学，2014，22(5): 16-23.

[17] 王佳，金秀，苑莹，等. 基于损失厌恶与模糊厌恶的分布鲁棒投资组合模型[J].系统工程理论与实践，2016，36(2): 288-296.

[18] 张茂军，南江霞，袁功林，等．基于损失厌恶的基金管理者的投资决策模型[J]. 管理工程学报，2014，28(4): 118-124.

[19] 韦来生，张伟平 贝叶斯分析[M].合肥中国科技大学出版社，2013.

[20] William T S， Thomas A P， Douglas N F. The triangular density to approximate the normal density: Decision rules-of-thumb[J]. Reliability Engineering and System Safety，2003，82(3): 331-341.

[21] Li Qi，Raccine J. 非参数计量经济学:理论与实践[M].叶阿忠，吴相波,译,北京:北京大学出版社，2015.

[22] Van den Steen E. Overconfidence by Bayesian-rational agents[J]. Management Science，57(5)：884-896.

[23] Ruppert D，Matteson D S. Bayesian data analysis and MCMC[M]//Ruppertp,Matteson D S. Statistics and data analysis for financial engineering，Springer Texts in Statistics， 2015：581-644.

[24] Shapiro A，Dentcheva D，Ruszczyński A. Lectures on stochastic programming: Modeling and theory[M]. 2ndEdition, Philadelphia:SIAM ,2014.

[25] Jose V R R. Assessing probability distributions from data[M]//Conhran J J. Wiley encyclopedia of operations research and management science，New York:John Wiley and Sons，2010:183-190.

[26] Price H J，Manson A R. Uninformative priors for Bayes theorem[C]//:21st International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering，Battimore, M D, August 4-9,2002.

[27] 张尧，关欣，孙杨,等. 考虑背景风险的项目投资决策[J]. 中国管理科学，2016，24(9):71-80.

Bayesian Evaluation and Selection Strategies in Venture Project Portfolio Decision Analysis

HU Zhi-jun1,2, PENG Fei3, LI Zhi-xia1

(1.School of Mathematics and Statistics，Guizhou University，Guiyang 550025，China;2. Guizhou Provincial Key Laboratory of Public Big Data，Guiyang 550025，China;3. School of Economics and Management，South China Normal University，Guangzhou 510631，China)

The venture capital market plays a significant role in providing capital to a new feasible business idea(new product, service, or retail concept) and businesses of different type. Project portfolio selection is an important decision in many venture capital companies, and practically all venture capitalists(VC) seek to creat value by selecting and executing portfolios of venture projects that consume resourse, and behavioral factors of the VC directly influences the result of the optimal portfolio selection. Most studies on project portfolio selection focus on identifying the “right” project portfolio under various criteria, such as reward and risk.In this paper a portfolio approach is taken to analyze the investment strategy of aVC. Considering the psych-ological characteristics of VC’s loss aversion from the perspective of prospect theory, a more practical portfolio optimization model that maximizes the expected utility of VC is constructed, and the model is transformed into a linear mixed integer programming problem by the Monte Carlo simulation method.Typically, the value of venture capital project is uncertain,and thus venture capitalist must take decisions based on ex ante estimates about what this future value will be. Due to estimation uncertainties, it is difficult to identify the truly best projects, whereby the selected portfolio is typically suboptimal. Furthermore, it can be shown that the value of the selected portfolio is systematically overestimated, causing the VC to experience post-decision disappointment. The phenomenon underlying post-decision disappointment is, in short, that the more the value of a project has been overestimated, the more probable it is that this project will be selected. In this paper, a Bayesian model framework to account for value uncertainties in project portfolio selection is developed. Our analytical and simulation results show that, in comparison with the straightforward portfolio selection based on ex ante value estimates, the explicit Bayesian modeling of estimation uncertainties tends to give more accurate project value estimates, resulting in a higher expected portfolio utility value, and eliminate the expected gap between the realized ex post portfolio utility value and the estimated ex ante portfolio utility value. Moreover, our results have shown that the Bayesian revision of value estimates decrease the level of disappointment that the VC can expect to experience.With the proposed Bayesian framework VC can gather more precise information about projects’ value and mitigate the experienced post-decision disappointment. Apart from the debiasing of value estimates, our frame-work could be extended by developing a model that accounts both value and cost uncertainties. This way number of targets of application could be substantially increased.

projects portfolio selection; loss aversion; Bayesian modeling; decision analysis

1003-207(2017)02-0030-10

10.16381/j.cnki.issn1003-207x.2017.02.004

2015-12-07；

2016-03-30

国家自然科学基金资助项目(71361003，71271090)；贵州省自然科学基金项目([2011]2102)；贵州省教育厅人文社科规划项目(13S5D005)

胡支军(1975-)，男(汉族)，贵州人，贵州大学数学与统计学院，教授，博士，研究方向：金融优化、决策分析等，E-maili:zjhu@gzu.edu.cn.

F830，O221

A