用常数列、零数列证明数列通项公式
2017-03-13 06:59:53贵州省七星关区北大附属实验学校551700
中学数学研究(江西) 2017年3期
贵州省七星关区北大附属实验学校 (551700) 魏 星
用常数列、零数列证明数列通项公式
贵州省七星关区北大附属实验学校 (551700) 魏 星
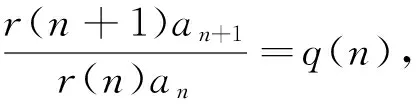
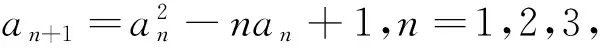

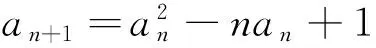

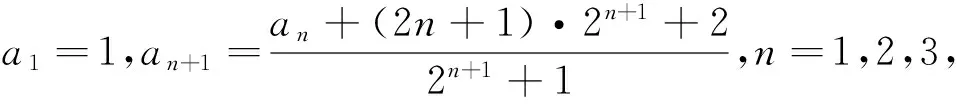
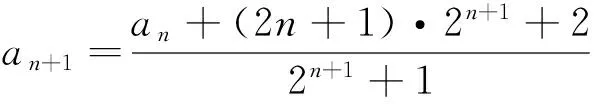
例3 设数列{an}满足
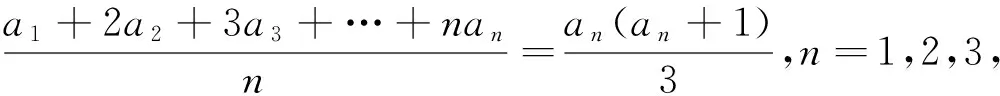
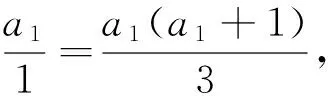
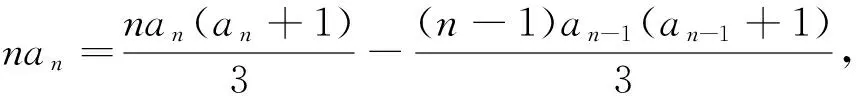
∵当n=2时,a1-2=0,∴an-(n+1)=0,即an=n+1.
例4 (2014年全国高考广东卷理19)已知数列{an}的前n项和为Sn,满足S3=15,Sn=2nan+1-3n2-4n(n∈N*).
(1)求a1,a2,a3;
(2)求{an}的通项公式.
解:由题设,得15=6a4-39,a4=9,n=1得a1=2a2-7,由an=Sn-Sn-1(n≥2)得an=[2nan+1-3n2-4n]-[2(n-1)an-3(n-1)2-4(n-1)](n≥2),解出


例5 已知数列{an}满足a1=1,(n+1)an=(n-1)an-1(n≥2,n∈N).求an的一个通项公式.(2016成都市三诊理17(1))


总之,一切数列{an},已知递推公式an+1=g(an),求通项公式an=f(n)(可求的话)都可试验,猜出后,用常数列、零数列证明,即递推公式an+1=g(an)化为an+1-f(n+1)=h(n,an)[an-f(n)]证明.
猜你喜欢
数理化解题研究(2022年22期)2022-08-30 06:37:58
河北理科教学研究(2021年1期)2021-06-07 07:49:14
草原歌声(2020年2期)2020-09-25 08:38:00
新高考·高二数学(2018年1期)2018-11-20 02:15:42
大灰狼(2018年5期)2018-06-20 14:49:32
小学生导刊(低年级)(2016年5期)2016-05-27 22:58:38
小朋友·快乐手工(2015年11期)2016-01-07 00:21:19
海关与经贸研究(2014年3期)2014-02-28 14:30:41
现代教育教学导刊(2009年2期)2009-10-14 06:37:52

