变载荷下采煤机摇臂传动系统动态特性分析

史红瑞

(山西煤炭建设监理有限公司,太原 030012)

采煤机摇臂传动系统的动态特性在不同负载作用下具有不同的特点和动力学行为。研究实际工作过程中传动系统的动态响应具有重要的意义,不仅可以指导实际生产,也能用于检查系统振动、噪声是否过大[1]。采煤机摇臂在生产加工完毕投入使用前,均要进行加载试验,以检验在特定条件下摇臂传动系统动态特性能否满足实际需求。利用动力学仿真软件ADAMS可以方便、快捷地模拟系统在不同负载作用下的动态响应,并根据需要更改试验参数,对于研究系统动态特性有着不可替代的优点。

1 采煤机摇臂传动系统仿真模型的建立

1.1 UG环境下的仿真模型建立

本文研究的摇臂模型结构是参考某煤机公司的MGTY750/1800型采煤机,其传动系统由两级定轴齿轮传动和两级2K-H型行星齿轮传动组合而成。在UG7.5中的GC齿轮工具箱中,通过输入齿轮的基本参数便可以完成各个齿轮的参数化建模[2]。并通过UG的拉伸和布尔运算等操作建立齿轮孔、两级行星架的模型。由于本文主要研究摇臂中齿轮的动态特性,故建模时忽略了轴承、端盖、挡圈和密封圈等次要零部件。最后在UG7.5中的装配环境下,将建立好的各个齿轮等部件通过适当的约束条件组装起来,形成与实际一样的装配仿真模型并导出为ADAMS可识别的Parasolid格式。

1.2 ADAMS环境下的动力学仿真模型建立

将从UG7.5中导出的Parasolid格式文件导入ADAMS/view环境中,并建立MODEL-1动力学模型,如图1所示,右侧为输入端,左侧为输出端。

图1 采煤机齿轮传动系统模型Fig.1 Gear system model of coal cutters

为各齿轮部件添加相应的材料和质量等参数。忽略摇臂对齿轮动态特性的影响,把机架设定为大地,前两级定轴齿轮系中的全部齿轮、第一级太阳轮、第一级行星架和第二级行星架添加相对于地面的旋转副;第一级行星系的三个行星轮和第二级行星系的三个行星轮分别添加相对于相应行星架的旋转副;在两个行星轮系的内齿圈添加相对于地面的固定副。

1.3 齿轮副接触力的仿真参数建立

为了对齿轮动力学参数进行仿真,需要引用ADAMS/Solve中的碰撞函数接触算法来定义齿轮副之间的接触力。它是通过函数库中的IMPACT碰撞函数来实现接触力的计算。计算公式如下:

(1)

式中：K为接触刚度,N/mm;x为齿间距离,mm;e为非线性指数,一般取1.5;Fs为阶跃函数,Cmax为达到最大穿透深度时的阻尼系数,N·s/mm;de为最大阻尼时的穿透深度,一般取0.1 mm。

阻尼系数一般为刚度系数的0.1%～1%,根据文献[3]可具体求得各齿轮副的接触刚度和接触阻尼,计算结果见表1。

表1各齿轮副接触刚度和接触阻尼

Table 1 Contact stiffness and damping between different gear pairs

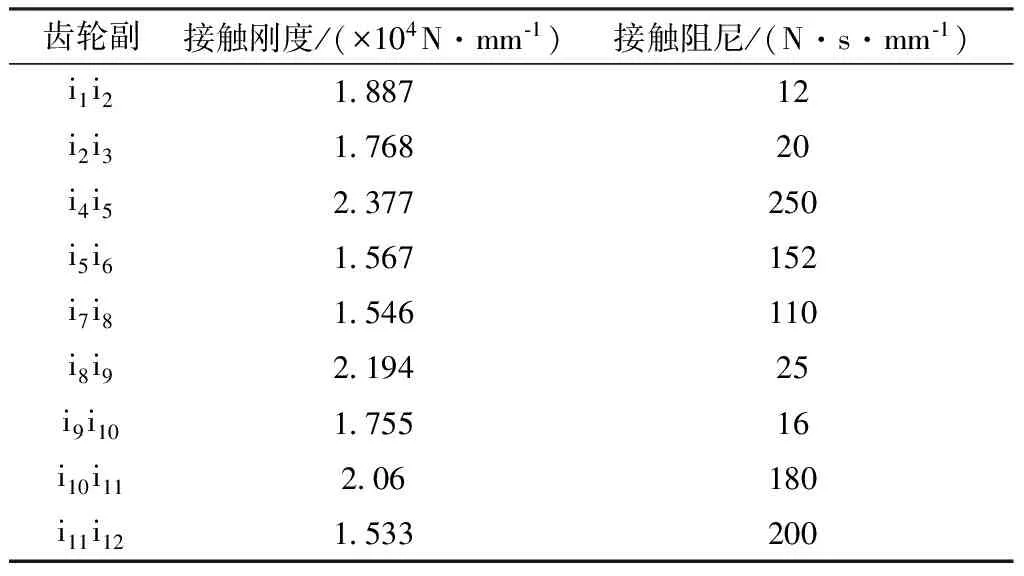
齿轮副接触刚度/(×104N·mm⁃1)接触阻尼/(N·s·mm⁃1)i1i21 88712i2i31 76820i4i52 377250i5i61 567152i7i81 546110i8i92 19425i9i101 75516i10i112 06180i11i121 533200

将计算得的各参数输入ADAMS中,整个系统形成了统一的整体,就构成了采煤机摇臂传动系统的动力学仿真模型。

1.4 传动系统刚柔耦合模型的建立

在系统仿真中,低速重载情况下可以把部件设为刚性体,但在高速运动状态下不能忽略部件的弹性变形,尤其是齿轮轮齿是一个变截面的悬臂梁,在高速情况下的变形尤为明显。所以为了仿真的准确性,将低速级的两个行星轮系设为刚性体,将高速级的两级定轴齿轮设为柔性体[4-5]。高速级前6个齿轮通过ADAMS/Flex模块进行相应设置,自动生成柔性体。而高速级最后一个齿轮是与太阳轮焊接而成,需要用ANSYS把它生成模态中性文件MNF,然后替换生成柔性体。至此建立了采煤机摇臂刚柔耦合动力学仿真模型。

2 特征频率计算及仿真结果

2.1 特征频率计算

齿轮系统属于旋转机械,需从时域和频域两方面研究其动态特性,因此必须计算齿轮系各齿轮的旋转频率和啮合频率这些特征频率。

啮合频率fm的计算公式如下：

(2)

式中：Z1、Z2为主、从动齿轮的齿数,N1、N2为主、从动齿轮的转速,r/s。

旋转频率即转速根据传动比公式求得,根据定轴传动比i1,2=z2/z1,2K-H型行星轮传动比i1,H=i3/i1+1,其中i3为内齿圈的齿数,i1为太阳轮齿数。滚筒额定转速为0.44 r/s,即第二级行星架转速为0.44 r/s,根据传动比依次算出各齿轮转速[6]。计算得的各齿轮旋转频率和啮合频率见表2。

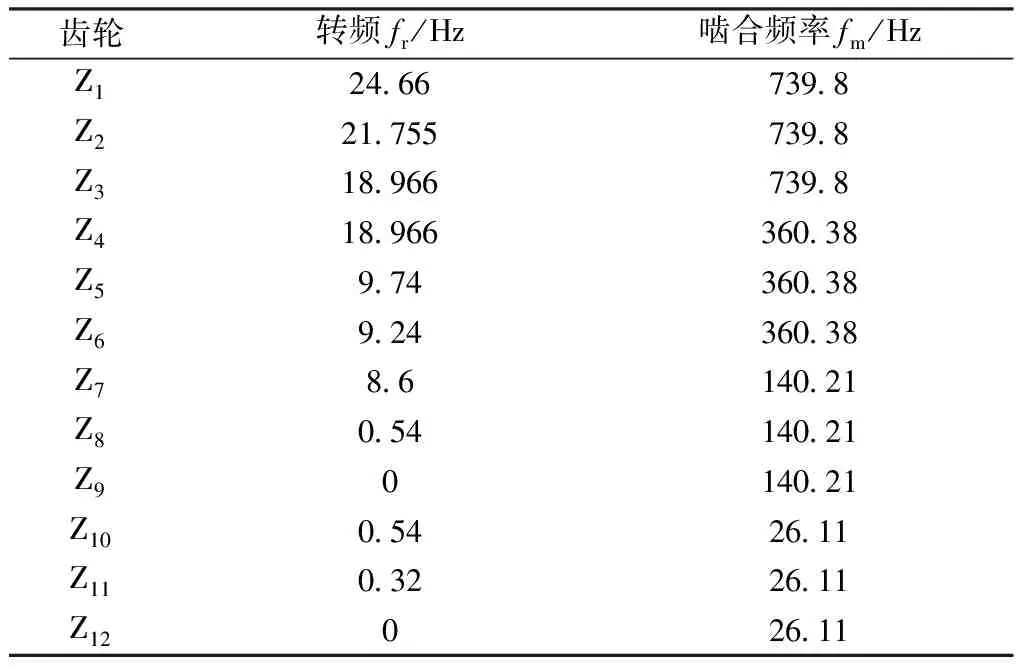
表2 各齿轮转频和啮合频率Table 2 Rotational frequency and meshing frequency of gears

2.2 仿真结果

根据产品手册计算出MGTY750/1800型号采煤机滚筒输出转矩T=2.7×105N·m,即滚筒额定载荷为T。本文分别采用空载、四分之一载、半载和满载四种载荷,作用在第二级行星架的质心上,研究具有代表性的齿轮Z4的振动特点。在Adams的simulation模块下设置仿真时间为60 s,步数为5 000步来进行仿真。通过ADAMS/PostProcsser输出时域图,并通过傅里叶变换得到相应的频域图。如图2—图5所示。

2-a 时域

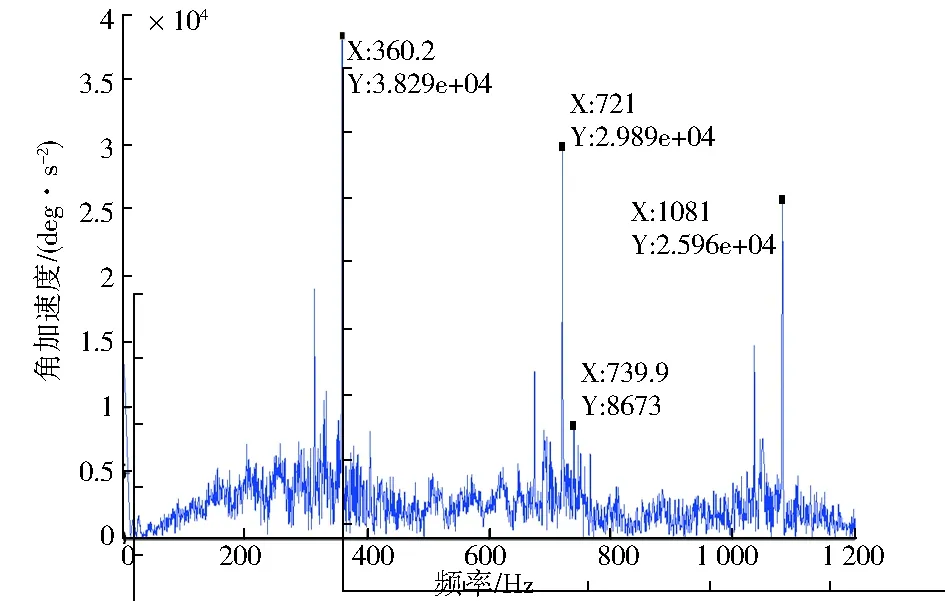
2-b 频域图2 空载情况下Z4质心扭振的时域图和频域图Fig.2 Time-domain plot and frequency-domain plot of torsional vibration of Z4 mass center under no-load condition

3-a 时域

3-b 频域图3 0.675×105 N·m载荷下Z4质心扭振的时域图和频域图Fig.3 Time-domain plot and frequency-domain plot of torsional vibration of Z4 mass center with load (0.675×105 N·m)

4-a 时域

4-b 频域图4 1.35×105 N·m载荷下Z4质心扭振的时域图和频域图Fig.4 Time-domain plot and Frequency-domain plot of torsional vibration of Z4 mass center with load (1.35×105 N·m)

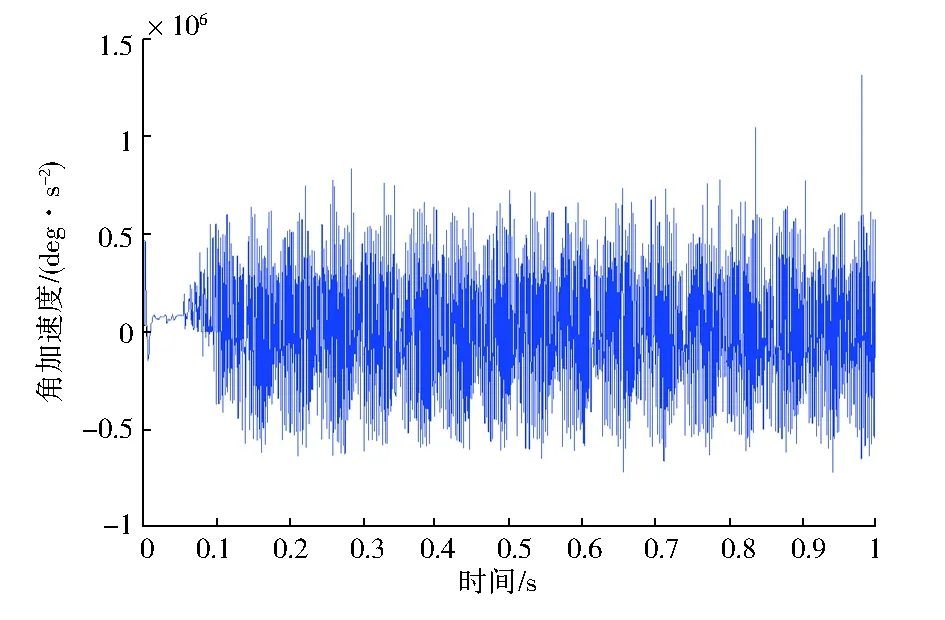
5-a 时域

5-b 频域图5 2.7×105 N·m载荷下Z4质心扭振的时域图和频域图Fig.5 Time-domain plot and Frequency-domain plot of torsional vibration of Z4 mass center with load (2.7×105 N·m)

3 仿真结果分析

3.1 时域分析

由图2-a齿轮4在空载下的角加速度时域图可知:在系统从0到0.1 s启动的过程中,齿轮振幅最大、振动最剧烈。0.1 s以后属于平稳阶段,虽然没有外界载荷作用,但仍存在着明显的振动,这主要是齿轮系统内部刚度激励的受迫振动。这种内部作用是一种摩擦力,会慢慢消耗系统的能量。由图2-a、图3-a、图4-a和图5-a分析可知,随着外载荷的增加,启动阶段对振动的作用逐渐减小,并且整个振动幅度逐渐增大。下面引入统计指标如均值、均方根值、峰峰值和方差来描述其振动特点[7],求出各情况统计数值如表3所示。

其中均值和均方根值反映了振动信号的能量大小,方差反映了振动信号的离散程度,峰峰值指信号中最大值和最小值之差。由表3可知,随着外载荷的增加,振动幅度越来越大,振动越来越杂乱。但随着每次载荷增加100%,均值依次增加34.49%,22.95%,16%,均方根值依次增加40.03%,31.7%,27.2%,方差依次增加77.03%,73%,61%,即扭转不随外载荷线性增加而是增加量越来越小。

表3 不同载荷作用下的统计指标值Table 3 Statistical value under different loads

3.2 频域分析

由图2-b、图3-b、图4-b和图5-b齿轮4在不同载荷下的频域图可以看出,它们均由四条谱线组成,分别列出各载荷下的频率和幅值,如表4所示。

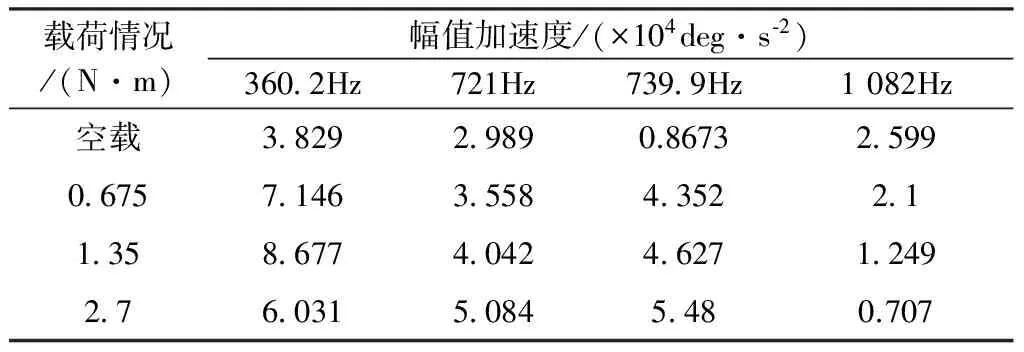
表4 不同载荷作用下主要频谱线和幅值加速度Table 4 Major frequency lines and amplitude accelerations under different loads

由表4可知,频谱图中主要频率不随外载荷变化。对比表2可知,频谱图中第一条谱线为360.2 Hz,该频率等于理论计算的第二级齿轮啮合频率360.38 Hz。第二条谱线721 Hz是第二级啮合频率的二倍频,第三条谱线739.9 Hz等于理论计算的第一级齿轮啮合频率739.8 Hz,第四条谱线1 082 Hz是第二级啮合频率的三倍频。齿轮的旋转频率和电机输入频率均没有在图中体现,是因为被幅值较大的啮合频率覆盖了。

输出为第二级传动系统齿轮Z4质心的角加速度,由表4可知,在空载情况下,频谱图上主要出现了第二级啮合频率360.2 Hz,以及其二倍频721 Hz和三倍频1082 Hz,也出现了第一级啮合频率739.9 Hz,但幅度上差了3个数量级,所以可知第一级啮合刚度激励在空载情况下对第二级传动系统的振动影响不大。

随着外载荷的成倍增加,第二级啮合频率360.2 Hz幅值先增加后减小,其二倍频721 Hz缓慢增加,三倍频1 082 Hz减小。第一级啮合频率739.9 Hz的幅值逐渐增加,在满载时与其他两条谱线达到了同一量级。由此可知,随着外载荷的增加,第一级啮合刚度激励对第二级传动系统振动的影响度也在增加,且它是振动的主要来源。

4 结论

本文使用ADAMS建立了采煤机摇臂传动系统的动力学模型,计算了传动系统各齿轮特征频率,对第二级齿轮Z4进行四种不同载荷作用的仿真,在ADAMS的PostProcsser模块输出Z4质心的角加速度时域及频域图。研究结果表明:

1)在空载情况下振动最为激烈的是在系统启动阶段,然后逐渐平稳,这是由于齿轮内部刚度激励冲击造成的,即使齿轮制造精度再高这个振动也是一直存在的;

2)根据统计指标显示,随着外载荷的成倍增加,振动幅度也在增加,但增加量却依次减小,振动也越来越杂乱;

3)频域分析可知,振动仅与齿轮的啮合频率有关,而与齿轮旋转频率和电机输入频率无关;

4)随着外载荷增加,第二级啮合频率及其倍频基本在减小,而第一级啮合频率在增加,故第一级啮合刚度激励对第二级传动系统振动的影响也在增加,且是振动的主要来源。

[1] 刘俊峰.试析电牵引采煤机的技术现状及发展趋势[J].煤炭科技,2016(1):95-97.

LIU Junfeng.Analysis to Current Situation and Development Trend of Electric Traction Shearer[J].Coal Science and Technology,2016(1):95-97.

[2] 刘群.电牵引采煤机截割部摇臂动力学特性分析及优化[D].太原:太原理工大学,2012.

LIU Qun.The Dynamic Characteristic Analysis and Optimization of Ranging Arm on Cutting Part of Coal Shearer[D].Taiyuan:Taiyuan University of Technology,2012.

[3] SOMOLINOS J A,FELIU V,Snchez L.Design,Dynamic Modeling and Validation of a New Three-degree-of-freedom Flexible Arm[J].Mechatronics,2002,12(7):919-948.

[4] 董海龙.刚柔耦合行星齿轮减速器仿真研究[D].沈阳:东北大学,2013.

DONG Hailong.Research on Rigid-flexible Coupling Simulation of Planetary Gear Reducer[D].Shenyang:Northeastern University,2013.

[5] 赵丽娟,马永志.刚柔耦合系统建模与仿真关键技术研究[J].计算机工程与应用,2010,46(02):243-248.

ZHAO Lijuan,MA Yongzhi.Study on Key Technologies in Modeling and Simulation of Rigid-flexible Coupled Multi-body System[J].Computer Engineering and Applications,2010,46(2):243-248.

[6] 徐玉秀.机械系统动力学分形特征及故障诊断方法[M].北京:国防工业出版社,2006.

[7] 陈绍军.基于虚拟样机的大型风电机组齿轮传动系统冲击特性分析[D].北京:华北电力大学,2008.

CHEN Shaojun.Transient Response Analysis of Larger Wind Turbine Commission System Based on the Virtual Prototype[D].Beijing:North China Electric Power University,2008.