高考函数导数压轴题分析及应对策略

高考函数导数压轴题分析及应对策略

☉广东省鹤山市第二中学 李立美

函数与导数是高中数学中极为重要的内容，其观点和方法也经常用于解决其他非函数类型的问题.其主要从以下几点进行考查：1.导数的概念以及利用导数解决一些简单类型的题目，如求极值，最值，切线方程，单调区间等；2.综合考查，将导数的内容与其他知识有机地结合起来，设计综合题.

从近几年高考函数与导数的大题得分情况来看，考生的得分普遍偏低.笔者通过近几年的教学实践，发现对于函数与导数的题目，学生普遍反映的主要问题有两个：一是思路不清晰；二是对解答函数与导数题目的方法掌握得不够，即使知道有几种方法，但是遇到具体题目时无从下手，不知选择何种方法.笔者从近几年的高考卷中选择几道压轴题，利用思路线帮助厘清答题思路，并且探讨高考数学函数与导数的答题方法.

策略一、转化与化归的运用

例1已知函数（fx）=2x3-3x.若过点P（1，t）存在3条直线与曲线y=（fx）相切，求t的取值范围.

解：设过点P（1，t）的直线与曲线y=（fx）相切于点（x0，y0），则y0=2-3x0，即切线的斜率为k=6-3，所以切线方程为y-=（6-3）（x-x）.将点P（1，t）代入，得t-y=（6x2-000 3）（1-x），整理得4-6+t+3=0.于是问题转化为此方程

0有三个不同的解.设g（x）=4x3-6x2+t+3，则“过点P（1，t）存在3条直线与曲线y=（fx）相切”等价于“函数g（x）有3个不同零点”.

因为g′（x）=12x2-12x=12x（x-1），

当x变化时，g（x）与g′（x）的变化情况如下：

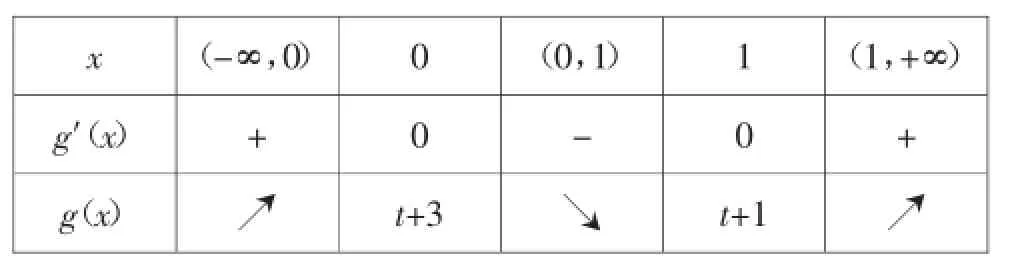
x（-∞，0）0（0，1）1（1，+∞）g′（x）+0-0+ g（x）↗t+3↘t+1↗

所以，g（0）=t+3是g（x）的极大值，g（1）=t+1是g（x）的极小值.

当g（0）＞0且g（1）＜0，即-3＜t＜-1时，因为g（-1）=t-7＜0，g（2）=t+11＞0，由于g（x）在区间（-∞，0），（0，1），（1，+∞）上单调，故g（x）分别在区间（-1，0），（0，1）和（1，2）上各有1个零点，即g（x）分别在区间（-∞，0），（0，1），［1，+∞）上各有1个零点.

综上可知，当过点P（1，t）存在3条直线与曲线y=f（x）相切时，t的取值范围是（-3，-1）.

在研究、解决数学问题时，采用某种手段或方法，使问题从一种情形转化为另一种情形，也就是转化到另一种情景使问题得到解决，这种转化是解决问题的有效策略，同时也是一种成功的思维方式.转化具有多样性、层次性和重复性的特点，遵循熟悉化、简单化、直观化的原则.本题的转化，使切线的条数转化为函数的零点个数，为解题铺平了道路

策略二、分离参数

分析：已知f（x）在（0，2）内存在两个极值点，求k的取值范围，无法直接求解，需要进行转化.函数f（x）在（0，2）内存在两个极值点⇒导数f′（x）=0在（0，2）内有两解⇒分离参数⇒y=k与y=g（x）在（0，2）内有两个交点⇒由g（x）的导数求极值点作出满足条件的图像⇒求出参数范围.

解：因为函数f（x）在（0，2）内存在两个极值点，

当x变化时，g′（x）与g（x）的变化情况列表如下：

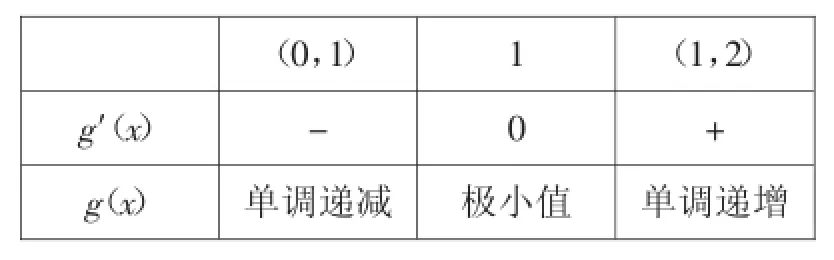
（0，1）1（1，2）g′（x）-0+ g（x）单调递减极小值单调递增

分离参数法是我们经常用到的一种方法.在解答的过程中思路清晰，其关键同样在于转化以及利用极值作出函数图像，利用数形结合.

策略三、最值法

（1）求a，b；

（2）证明：f（x）＞1.

分析：由题可得f（1）=2，f′（1）=e，进而求出a，b；第（2）问题属于证明题，不等式左边比较麻烦，需要对不等式进行化简，再证明.

解：（1）略.

（2）证明：将不等式转换成g（x）＞h（x）的形式⇒［g（x）］min＞［h（x）］max.

所以g（x）＞h（x），即f（x）＞1.

此种方法对于一些既含有指数函数，又含有对数函数的题目比较实用，通过化简将它们分离，对于后面求最值降低难度.但此种方法需要进行合适的变形，这时需要读者多尝试几种变形.

策略四、构造函数

例4已知函数f（x）=-2（x+a）lnx+x2-2ax-2a2+a，其中a＞0.

（1）设g（x）是f（x）的导函数，讨论函数g（x）的单调性；

（2）证明：存在a∈（0，1）使得f（x）≥0在区间（1，+∞）内恒成立，且f（x）=0在区间（1，+∞）内有唯一解.

解析：（1）（略）.

（2）证明：由f（′x）=2（x-a）-2lnx-2（ 1+）=0，解得a=

当a=a0时，有f′（x）=0，f（x0）=φ（x0）=0，由（1）知，f′（x）在区间（1，+∞）上单调递增，故当x∈（1，x0）时，f′（x）＜0，从而f（x）＞f（x0）=0；当x∈（x0，+∞）时，f′（x）＞0，从而f（x）＞f（x0）=0.所以，当x∈（1，+∞）时，f（x）≥0.

综上所述，存在a∈（0，1），使得f（x）≥0在区间（1，+∞）内恒成立，且f（x）=0在区间（1，+∞）内有唯一解.

构造函数是解决导数问题的常用手段，巧妙地构造函数能使我们对问题有更加深刻的认识，是解题的锐利武器.常用的构造方法有移项作差、结构抽象、确定主元等.本题的匠心之处在于两次构造函数.尤其是第一次以解代参，即以f′（x）=0时的a值代替f（x）中的参数a构造函数φ（x），它在（1，e）上有零点，且当a=a0时，有f′（x）=0，f（x0）=φ（x0）=0是解题的关键.

策略五、设而不求

又f′（-1）＜0，f′（0）＞0，故f′（x）=0在（-2，+∞）上有唯一实根x0，且x0∈（-1，0）.当x∈（-2，x0）时，f′（x）＜0；当x∈（x0，+∞）时，f′（x）＞0，从而当x=x0时，f（x）取得最小值.

由f（′x）0=0，得ex0 =，ln（x0+2）=-x0，故（fx）≥（fx）0

例5已知函数f（x）=ex-ln（x+m）.当m≤2时，证明f（x）＞0.

证明：当m≤2，x∈（-m，+∞）时，ln（x+m）≤ln（x+2），故只需证明当m=2时，f（x）＞0.当m=2时，函数f′（x）=ex-

综上，当m≤2时，f（x）＞0.

求方程f′（x）=0的根在解导数问题中是承上启下的一步，此时受阻，解题将难以为继.像本题中，虽然f′（x）= 0的根的确存在，可无论如何都求不出来.怎么处理？上述解答告诉我们，可以虚设零点，但设而不求，只利用其满足的条件就能到解题目的.这种“设而不求”的方法，在数学中是经常遇到的，特别是解析几何中直线与圆锥曲线的交点.

策略六、分类讨论

例6已知函数（fx）=x2-ax（3a＞0），x∈R.

（1）求f（x）的单调区间和极值；

（2）对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）·f（x2）=1，求a的取值范围.解：（1）单调递减区间为（-∞，0）和（，+∞），单调递增为

+∞），都存在x2∈（1，+∞），使得（fx）1·（fx）2=1”等价于A⊆B，显然，0∉B.

下面分三种情况讨论：

分类讨论是将一个较复杂的数学问题分解成若干个基础性问题，通过对基础性问题的解答来实现解决原问题的思维策略.分类讨论要坚持不重不漏、标准统一的原则.分类讨论的步骤是：确定对象、合理分类、逐类讨论、归纳总结.本题中，两个集合A、B中的元素是倒数关系，能否取导数取决于它是否为零.又因为x1∈（2，+∞），∈（1，+∞），所以按照＞2、1≤≤2、＜1三种情况讨论.

总之，导数及其应用是高中数学的重要内容，是进一步学习高等数学的重要基础.在高考试卷上，它是以压轴题的形式呈现的.由于其信息量、思维量、运算量都比较大，需要较高的数学分析、解决问题的能力.由以上各例可以看出，上述几种方法不是相互排斥的，而是相辅相成的.在具体问题中，往往是几种方法互相配合、共同发力.只要运用得当，就能收到良好的效果.