基于区间分析的机械结构稳健优化设计

陈 静，吴振扬 ，王文博，闫 昊

(1.桂林理工大学 a.广西矿冶与环境科学实验中心；b.机械与控制工程学院，广西 桂林 541004；2.中国能源建设集团江苏省电力建设第三工程有限公司 热机专业公司，江苏 镇江 212001)

基于区间分析的机械结构稳健优化设计

陈 静1a,1b，吴振扬2，王文博1b，闫 昊1b

(1.桂林理工大学 a.广西矿冶与环境科学实验中心；b.机械与控制工程学院，广西 桂林 541004；2.中国能源建设集团江苏省电力建设第三工程有限公司 热机专业公司，江苏 镇江 212001)

为了提高机械结构稳健优化设计工程适用性，分析机械结构稳健优化设计过程，综合考虑目标函数和约束的稳健性、设计变量的离散性、设计变量区间的公差约束，建立基于区间分析的机械结构稳健优化数学模型，结合机械结构稳健优化设计特点，构建连续型设计变量和离散型设计变量二级稳健优化设计框架和流程，最后通过实例验证了该方法的有效性。

区间分析；机械结构；稳健优化；公差

0 引言

机械结构设计过程中，存在各种不确定性因素，如材料特性、结构尺寸、载荷等的波动变化会影响产品质量特性。影响产品的质量特性的不确定性因素可以分成两类，可控制因素和不可控制因素。可控制因素也称为设计变量，如结构尺寸、材料的种类等；不可控制因素就是指在设计及加工的过程中人为不好控制的因素，也称为设计参数，如载荷、材料特性等，或者是即使可以控制，也需要大量的时间或者金钱成本。稳健设计[1]是研究在考虑不确定性因素的前提下降低不确定性因素对产品质量的影响。稳健优化设计通过增强对可控制因素的控制，使产品性能受不确定因素变化的影响较小，在工程设计问题中得到广泛应用[2-3]。

根据对不确定因素处理方式的不同，稳健优化设计可被分成概率和非概率稳健优化设计两种。概率稳健优化设计，需要预先知道不确定因素的概率密度函数，并且在实际工程中，某些不确定因素的精确概率分布很难获得[4]。对于很难找到其概率分布的不确定参数可以用区间来描述。因此，基于区间分析的非概率稳健优化设计[5-6]在工程中的应用越来越广泛。

在机械结构的优化设计方面，国内外学者运用区间分析方法做了大量研究探索。孙伟等[7]直接利用区间分析算法求得在不确定因素影响下变化后的目标函数及约束的上下界，采用确定性的区间数序排列方法和基于度的区间数序排列方法对稳健优化的数学模型进行转换,并且能够求得满足决策者任意偏好信息的稳健解。董荣梅等[8]能够根据设计者的偏好求解具有任意稳健性指标的优化解。许焕卫等[7]提出利用最大波动法分析目标函数及约束的稳健性。Jinglai Wu等[9]提出用高阶泰勒包含函数来解决区间运算的扩展问题。但是，目前稳健优化的数学模型主要针对连续型设计变量，在机械结构的设计变量中，结构尺寸多数为整数，还有推荐的尺寸系列或经验值，并且结构尺寸还有公差，因此，连续型设计变量的优化结果并不能直接使用。为了提高机械结构稳健优化的工程适用性，本文在文献[7-8]提出的稳健优化的数学模型的基础上，同时考虑离散型设计变量和设计变量的公差，研究基于区间分析的机械结构稳健优化设计。

1 机械结构稳健优化工程设计过程

(1)连续型设计变量稳健优化设计

基于连续型设计变量和设计参数进行稳健优化设计，得到连续型设计变量的优化结果。

(2)结构尺寸优化设计

对于设计变量中的结构尺寸，首先，将连续型设计变量的优化结果圆整后，再取推荐的尺寸系列或经验值，常用的取值方法有取最近的值、取最近的大值、取最近的小值等方法。结构尺寸经取值后,是否能达到稳健设计的目标是不确定的。

(3)结构尺寸公差设计

结构尺寸可按标准公差系列确定公差，标准公差系列由基本尺寸的标准公差和公差等级构成，国家标准对基本尺寸进行了分段，结构尺寸的标准公差值依据其基本尺寸所处的尺寸分段来确定。因此,结构尺寸是区间数，即设计变量值是区间数。此时,特别是结构尺寸中的自由尺寸，其公差值较大，是否还能达到稳健设计的目标也是不确定的。

2 基于区间分析的机械结构稳健优化设计数学模型

2.1 目标函数的稳健性

2.1.1 优化模型

目标函数的稳健性指同时优化目标的均值和波动，并考虑结构尺寸的公差约束，建立含不确定因素的优化模型为：

s.t.

hj(X,Y)=0;j=1,2,…,m

Xmin+ΔX1≤X≤Xmax-ΔX2

(1)

2.1.2 结构尺寸的公差约束

由于结构尺寸公差有对称公差和不对称公差，采用上偏差ΔX1和下偏差ΔX2表达结构尺寸公差，用区间数表达包含公差的结构尺寸，采用区间数的运算，表达包含公差的结构尺寸的约束，其表达式为：

(2)

2.1.3 不确定性目标函数的确定性转换

i=1,2,…,t

(3)

(4)

式中，Ac、Ar、Bc、Br分别为区间AI和BI的中值与半径。

由式(4)可知，当且仅当区间BI的中值和半径都小于区间AI的中值和半径时，区间BI才优于区间AI。对于BI，其中值和半径的计算公式为：

(5)

式中，

(6)

(7)

(8)

式中，λ为权重系数，0≤λ≤1。

2.2 不等式约束的稳健性

(9)

(10)

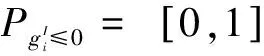
(11)

2.3 等式约束的稳健性

(12)

式(12)可以转化为两个不等式约束：

(13)

若设计者要求等式约束的稳健性不小于φj时，式(13)可以转化为[4]：

(14)

3 基于区间分析的机械结构稳健优化设计

3.1 机械结构稳健优化设计求解策略

根据上述目标函数及约束的稳健性分析，将不确定性的优化转化为确定性的优化问题后,优化模型呈现多目标、非线性的形式。罚函数法是一种将有约束的优化转化成无约束优化的方法，其结构简单、计算方便、求解效率高；遗传算法是一种启发式的随机搜索方法，其全局搜索性强、搜索效率较高。因此，本文采用罚函数法将有约束的优化转化成无约束优化问题，采用遗传算法对优化问题进行求解。

3.2 机械结构稳健优化设计框架和流程

3.2.1 基于区间分析的机械结构稳健优化设计框架

依据基于区间分析的机械结构稳健优化设计数学模型,结合机械结构稳健优化工程设计过程，将机械结构稳健优化设计框架分为连续型设计变量稳健优化、离散型设计变量稳健优化两个阶段。

3.2.2 基于区间分析的机械结构稳健优化设计流程

依据基于区间分析的机械结构稳健优化设计框架,建立基于区间分析的机械结构两级稳健优化设计流程图如图1所示。

(1)连续型设计变量稳健优化设计

①在设计变量区间随机选取X，产生初始种群。

②依据设计参数区间，计算目标函数的间，进行不确定目标函数确定性转换，设置目标权重λ，采用加权法将双目标优化转化为单目标优化。

③依据设计参数区间，计算约束区间，计算约束的区间可能度，进行不确定约束确定性转换。

④采用罚函数法将有约束优化转化为无约束优化，采用遗传算法对无约束优化问题进行求解；如果收敛或者达到最大迭代次数，得到设计变量X的连续型优化解；否则，根据X和公差查标准得上偏差ΔX1和下偏差ΔX2。

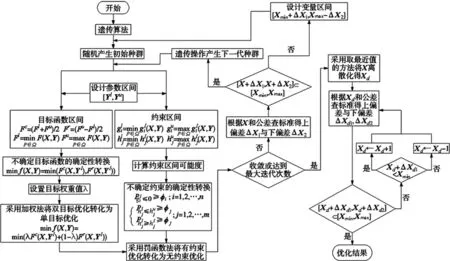
图1 基于区间分析的机械结构稳健优化设计流程图

(2)离散型设计变量稳健优化设计

①依据连续型设计变量X的优化解，采用取最近的值的方法，将X离散化得Xd。

②根据Xd和公差查标准得上偏差ΔXd1和下偏差ΔXd2。

依据基于区间分析的机械结构稳健优化流程可知，①通过区间数学的包含关系，判断含公差的设计变量是否在设计变量区间，来考虑设计变量的公差约束；②设计变量离散化策略，采用取最近值的方法，得到离散化设计变量；③当离散型设计变量不满足设计变量约束时，采用取最近值的方法对其进行调整。

4 算例

悬臂梁结构如图2所示，在悬臂梁上分别作用两个集中载荷F1和F2。

图2 悬臂梁结构

悬臂梁的优化问题要求在严格满足强度和刚度的约束条件下，悬臂梁的造价最低，将悬臂梁的造价最低转化为体积最小的问题，则悬臂梁的优化问题的数学模型为：

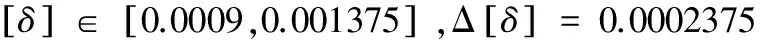
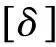
依据基于区间分析的机械结构稳健优化设计流程，采用两种方法对该优化问题进行求解，分别是不考虑公差的稳健优化解法(M1)和本文提出的方法(M2)，优化结果如表1所示，强度和刚度如表2所示；依据式(11)计算不等式约束的稳健性，不等式约束稳健性如表3所示，其中该问题的三个约束函数的稳健性指标分别用R1、R2、R3表示。

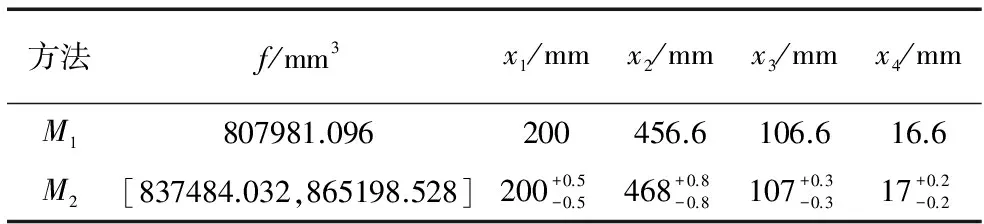
表1 优化结果

表2 强度和刚度

表3 不等式约束稳健性

由表1可知，本文提出方法所得的优化结果为带有公差的整数，可以直接用于工程设计。由表1、表2、表3可知，不考虑公差的稳健优化解好，但是，本文所提出方法所得的优化结果的约束稳健性高、强度和刚度高，因此，本文提出方法所得的优化结果损失了目标函数，但稳健性得到了提高。上述结果表明，要获得较大的稳健性，需要牺牲部分目标函数。

5 结论

结合机械结构稳健优化工程设计过程的特点，在考虑目标函数和约束的稳健性的基础上，同时考虑设计变量的公差、设计变量的离散性，建立基于区间分析的机械结构稳健优化设计模型，构建连续型设计变量和离散型设计变量的二级稳健优化设计框架和流程。本文提出方法所得的优化结果，可以直接用于机械结构的设计，并且，相对于不考虑结构尺寸公差的方法，稳健性好，提高了机械结构稳健优化的工程适用性。

[1] TaguchiG.Quality engineering through design optimization[M].NewYork:Krauss International Press,1986.

[2] 伍建军,吴佳伟.柔顺平行四杆机构多目标稳健优化设计[J].组合机床与自动化加工技术,2016(5):62-66.

[3] 迟建华,王承刚,田志涛,等.摆线针轮行星传动多目标稳健优化设计[J]. 组合机床与自动化加工技术,2016(5):32-35.

[4] 董荣梅,孙伟,许焕卫.基于区间分析的非概率稳健优化设计[J].大连理工大学学报,2011,51(1):51-55.

[5] 刘玉琳,陈文亮,鲍益东,等.基于区间分析的多边形坯料形状非概率稳健优化[J].机械工程学报,2014,50(10):65-71.

[6] J WU.A robust optimization for the frequency and decoupling ratio of a powertrain mounting system based on interval analysis[J].International Journal of Automotive Technology,2012,13(3):409-422.

[7] Wei sun,Rongmei Dong,Huanwei Xu.A Novel Non-Probabilistic Approach using Interval Analysis for Robust Design Optimization[J].Journal of Mechanical Science and Technology,2009,23(12):3199-3208.

[8] 许焕卫,孙伟,张旭.基于最大波动分析的稳健设计[J].农业机械学报,2008,39(12):162-165.

[9] Jinglai Wu,Zhen Luo,Nong Zhang,et al.A new interval uncertain optimization method for s-tructuresusing chebushev surrogate model[J].Computers and Structures.2014,146:185-196.

[10] DING Rui,LIN D K J,WEI Duan.Dual-response surface optimization:A weighted MSE approach [J].Quality Engineering,2004,16(3):377-387.

(编辑 李秀敏)

Robust Optimal Design of Mechanical Structure Based on Interval Analysis

CHEN Jing1a,1b, WU Zhen-yang2, WANG Wen-bo1b,YAN Hao1b

(1.a.Guangxi Scientific Experiment Center of Mining, Metallurgy and Environment;b.School of Mechanical and Control Engineering,Guilin University of Technology, Guilin Guangxi 541004,China;2. Engine Professional Company,China Energy Engineering Group Jiangsu No.3 Electric Power Construction Co., Ltd.,Zhenjiang Jiangsu 212001, China)

In order to improve the engineering applicability of robust optimization design of mechanical structure, analyzed the process of robust optimization design of mechanical structure, Comprehensive consideration of the robustness of objective function and constraint function, discreteness of design variables and tolerance constraints of design variable interval, to build the robust optimization mathematical model of mechanical structure based on interval analysis, to build two levels of robust optimization design frameworks and processes of continuous and discrete design variables with the features of robust optimization design of mechanical structure. Finally, an example was used to verify the effectiveness of the given method.

interval analysis; mechanical structure; robust optimization; tolerances

1001-2265(2017)02-0041-04

10.13462/j.cnki.mmtamt.2017.02.011

2016-05-29；

2016-07-04

陈静(1963—)，女，重庆人，桂林理工大学副教授，研究方向为不确定性多学科优化，(E- mail) jingc812@163.com。

TH122；TG65

A