Cyclic strength of sand under a nonstandard elliptical rotation stress path induced by wave loading＊

Zhong-tao Wang (王忠涛), Peng Liu (刘鹏), Dongsheng Jeng, Qing Yang (杨庆)

1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China, E-mail:zhongtao@dlut.edu.cn

2. Griffith School of Engineering, Griffith University Gold Coast Campus, Queensland, QLD 4222, Australia

(Received January 31, 2015, Revised July 1, 2015)

Cyclic strength of sand under a nonstandard elliptical rotation stress path induced by wave loading＊

Zhong-tao Wang (王忠涛)1, Peng Liu (刘鹏)1, Dongsheng Jeng2, Qing Yang (杨庆)1

1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China, E-mail:zhongtao@dlut.edu.cn

2. Griffith School of Engineering, Griffith University Gold Coast Campus, Queensland, QLD 4222, Australia

(Received January 31, 2015, Revised July 1, 2015)

The principal stress rotation is one of the most important features of the stress state in a seabed subjected to wave loading. Most prior investigations focused their attention on the cyclic behaviour of soil deposits under the circular rotation stress path based on the analytical solutions for a seabed of infinite thickness. In this paper, the nonstandard elliptical, i.e., non-circular, rotation stress path is shown to be a more common state in the soil sediments of a finite seabed with an alternating changeover in stress due to a travelling regular wave. Then an experimental investigation in a hollow cylinder triaxial-torsional apparatus is conducted into the effect of the nonstandard elliptical stress path on the cyclic strength. A special attention is placed on the difference between the circular rotation stress path and the elliptical rotation stress path. The results and observations show that the shear characteristics for the circular rotation stress path in the literature are not applicable for analyzing the cyclic strength of sand in a finite seabed, and also indicate that due to the influence of three parameters about the size and the shape of a nonstandard ellipse, the cyclic strength under a nonstandard elliptical rotation stress path is evidently more complex and diversified as compared with that under a circular rotation stress path. Especially the influence of the initial phase difference on the cyclic strength is significant.

Principal stress rotation, cyclic strength, nonstandard elliptical rotation stress path, wave loading

Introduction

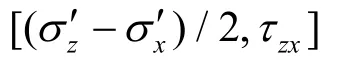
The seabed of infinite thickness is only an ideal case. Hsu and Jeng[14]developed a set of general solutions for the porous seabed of finite thickness. Their analytical solutions indicate that the thickness of the seabed plays a dominant role in the evaluation of the wave-induced response of the seabed. Later, the problem of the wave-induced dynamic response of the finite seabed has received much attention[15-22]. Meanwhile, laboratory experiments and field measurements of the wave-induced pore pressure and the effective stresses were also conducted on a porous soil of finite thickness. But the corresponding stress path for the seabed soil with finite thickness is not further examined, and there are not experimental evidences of its effects on the characterisation of the soil behaviour. Therefore, it is necessary to re-explore the work by Ishihara and Towhata[2]through theoretical and experimental investigations of a finite seabed.

The objective of this paper is to investigate the cyclic strength of the sand under the nonstandard elliptical rotation stress path induced by the wave loading. Before that, the nonstandard elliptical, i.e., non-circular, rotation stress path will be shown to be a more common state in the seabed soil of finite thickness due to the linear regular wave. And three parameters that determine the size and the shape of a nonstandard ellipse will be deduced. Then by using a hollow cylinder triaxial-torsional apparatus, the effects of the three parameters on the cyclic strength will be investigated separately and an experimental comparison between the circular stress path and the elliptical stress path will be made to demonstrate the necessity of adopting the elliptical rotation stress path for evaluating the cyclic strength of the sand in a finite seabed.

1. Nonstandard elliptical rotation stress path in the seabed

Considering the initial earth stress, the effective stress in the soil sediment can be expressed as

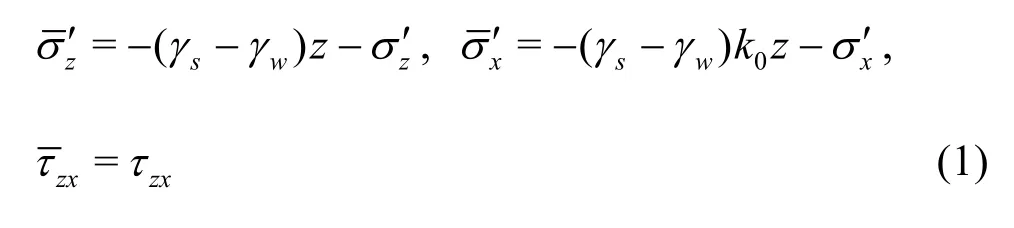
whereγsandγware the unit weights of soil and water, respectively, andk0is the lateral earth pressure coefficient at rest.σz′,σx′andτzxare the waveinduced effective stresses for 2-D progressive waves, as described by Hsu and Jeng[14].zis the vertical position in the seabed.

The normal stress difference is expressed as

where

whereRe{}indicates that only the real part of the complex solution is to be considered.eiϕ=cosϕ+ isinϕ, whereϕ=kx−ωt.kis the wave number,ωis the angular frequency of the wave,tis the time andxis the horizontal position.p0=γwH/ 2cosh(kd)represents the amplitude of the wave loading on the surface.His the wave height of the short-crested waves, anddis the water depth.M1can be deduced as follows based on the analytical solution of the dynamic response of the seabed under 2-D progressive waves by Hsu and Jeng[14]

The complex numbersC1throughC6are six coefficients, and the parameterδcan be interpreted as themodified wave number due to the wave action on a porous seabed.λis a parametric coefficient reflecting the saturation degree of the soil. All these parameters are described in detail in Hsu and Jeng[14]. BecauseM1is a complex number, it can be expressed as

A1is the real part, andB1is the imaginary part.

Equation (4) can be expressed as

whereais the amplitude of (σz′−σx′)/2andθ1is the initial phase angle of(σz′−σx′)/2.

Substituting Eq.(7) into Eq.(2), we have

The shear stress can be expressed as

where

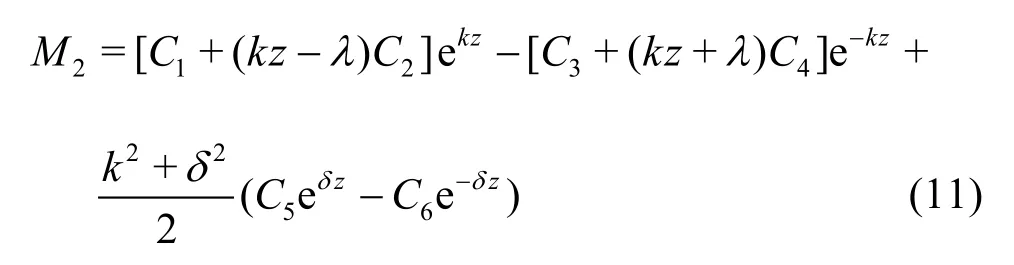
BecauseM2is a complex number, it can be expressed as

A2is the real part, andB2is the imaginary part.

Then, Eq.(10) can be expressed as

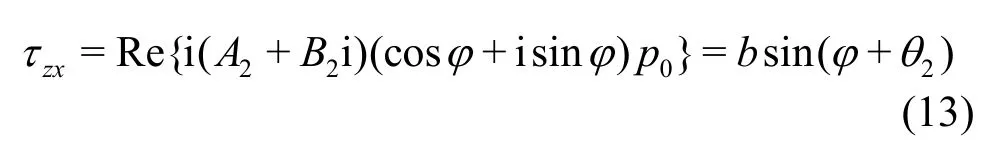
where

wherebis the amplitude ofτzxandθ2is the initial phase angle ofτzx.

In summary, we have

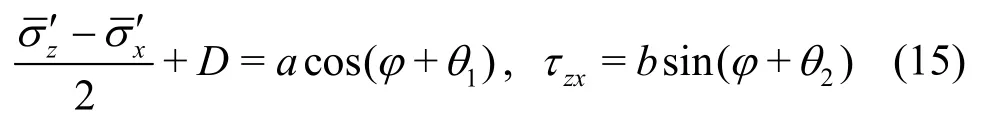
Equation (15) leads to

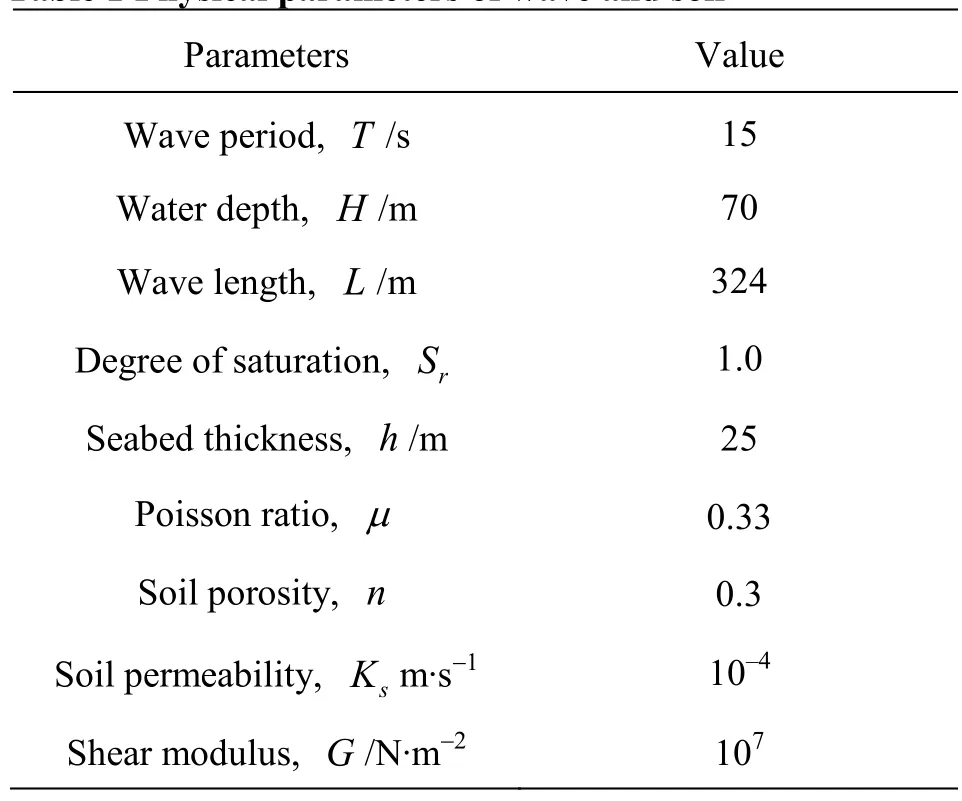
Table 1 Physical parameters of wave and soil

Figure 1 shows the stress path at various depths of the finite seabed, and Fig.2 shows the vertical distributions ofa,bandθversusz/h. Also plotted in Fig.2 are the numerical results obtained from the analytical solutions for the infinite seabed. The following observations can be made:

(1) The orientation of the principal stress rotates continuously. Furthermore, at the largest seabed depth,ais not equal tobaccording to the numerical results obtained from the analytical solutions for the finite seabed.

(2) Whenθ≠0, the stress paths form a nonstandard ellipses across the soil depth. As shown in Fig.1(b), the nonstandard degree of an ellipse is greater, near the seabed surface.

(3) The size and the shape of the ellipse vary with the depth of the finite seabed as shown in Fig.1.

(4)ais equal tobandθ=0when the thickness of the seabed becomes infinite as shown in Fig.2. The corresponding stress paths across the soil depth are not presented in this paper, but will precisely be a series of circles according to Eq.(15).

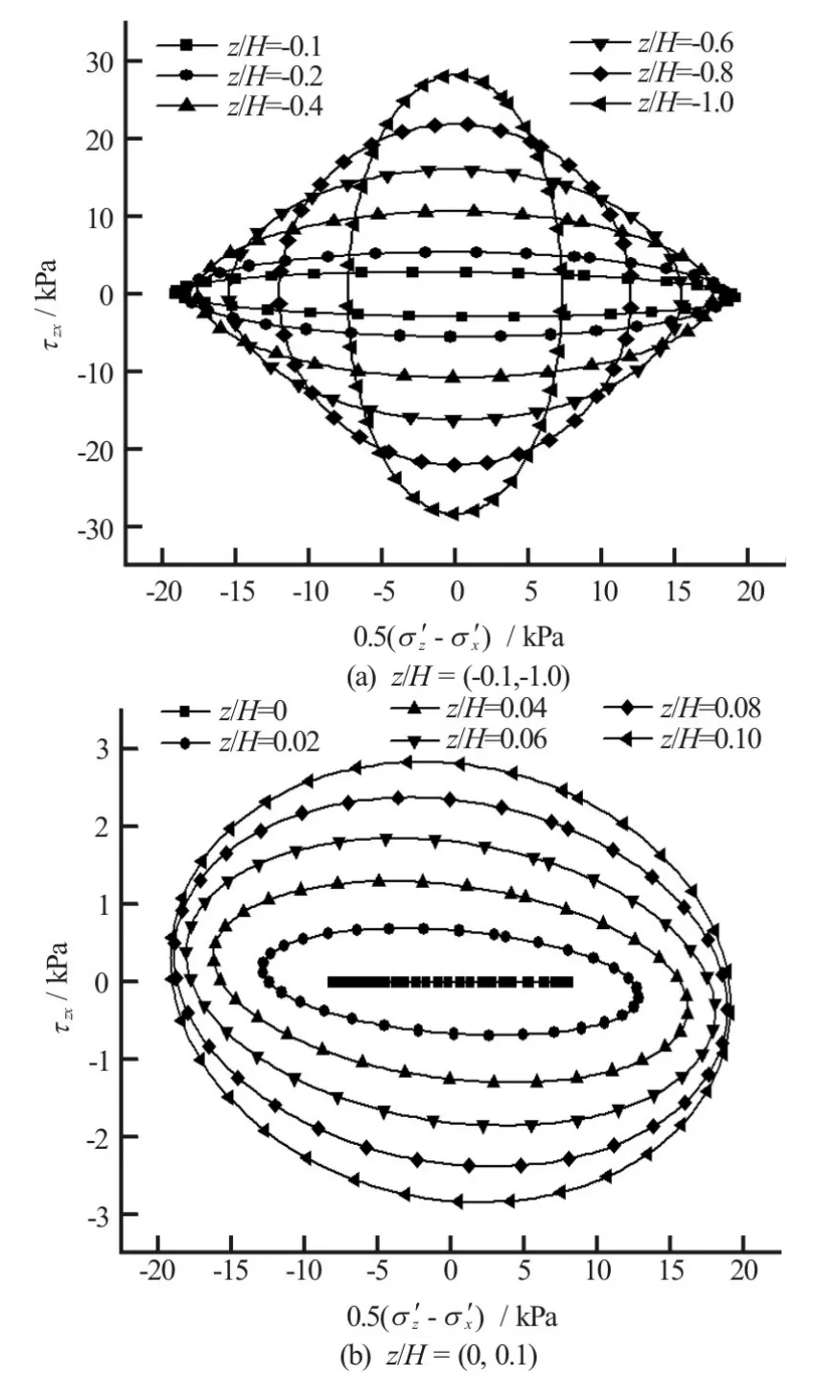
Fig.1 Stress paths on the [(′−)/2,τzx]plane at the different depths of the seabed. (theY-axis scale is enlarged 5 times for clarity in Fig.1(b))

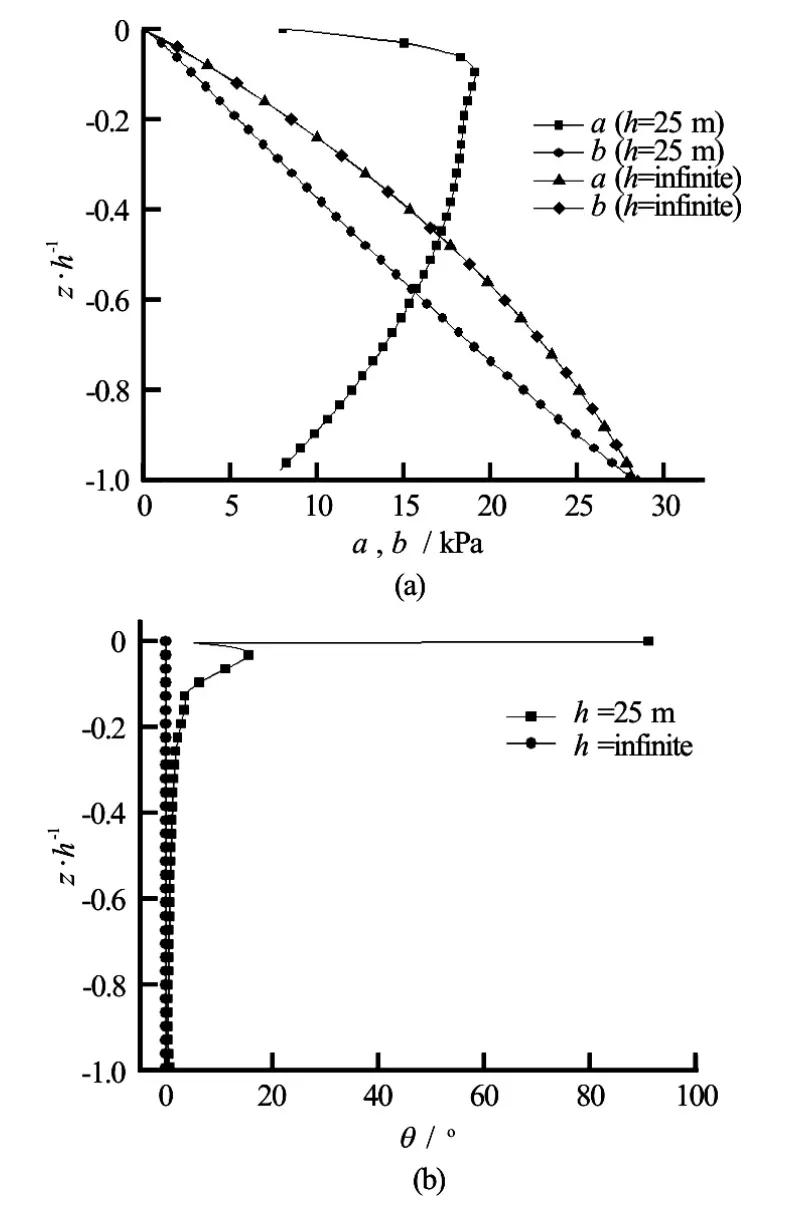
Fig.2 Vertical distributions ofa,bandθversusz/h

The nonstandardelliptical rotation stress path is shown to be more common than the circular rotation stress path in the finite seabed under a regular wave loading. Therefore, it is necessary to conduct undrained hollow cylinder triaxial-torsional tests to study the cyclic strength under a nonstandard elliptical rotation stress path. The cyclic strengthτfis defined as the cyclic shear stressτcycneeded to reach a specified value of the accumulated strain in a given number of uniform cycles. The number of stress cycles to the failure of the specimen is defined asNf. There is a correspondence between the cyclic shear stressτcyc, the cyclic strengthτfand the failure cyclesNf, and with a largerNf,τcycandτfare smaller.

2.1Test process

The testing is carried out with reconstituted specimens of Chinese Fujian Standard Sand, with a mean particle diameterD=3.4× 10−4mand the specific

50gravityGs= 2.643 . A ll spe cimens are isotro pically consolidatedunderameannormaleffectivestress

2. Investigation of cyclic strength through hollow cylinder triaxial-torsional tests

=100 kPaand a coefficient of the intermediate principal stressb=0.5. A loading frequency of 0.1 Hz is used for all tests. The initial relative densityDris controlled to be 30%. The details of the method of the hollow cylinder triaxial-torsional tests can be found in Yang et al.[6]. In the course of experiment,a,bandθare controlled independently to achieve a nonstandard elliptical or circular rotation stress path. The uniform failure criterion is defined as 5% of the generalised shear strain.

Table 2 Tests for comparison

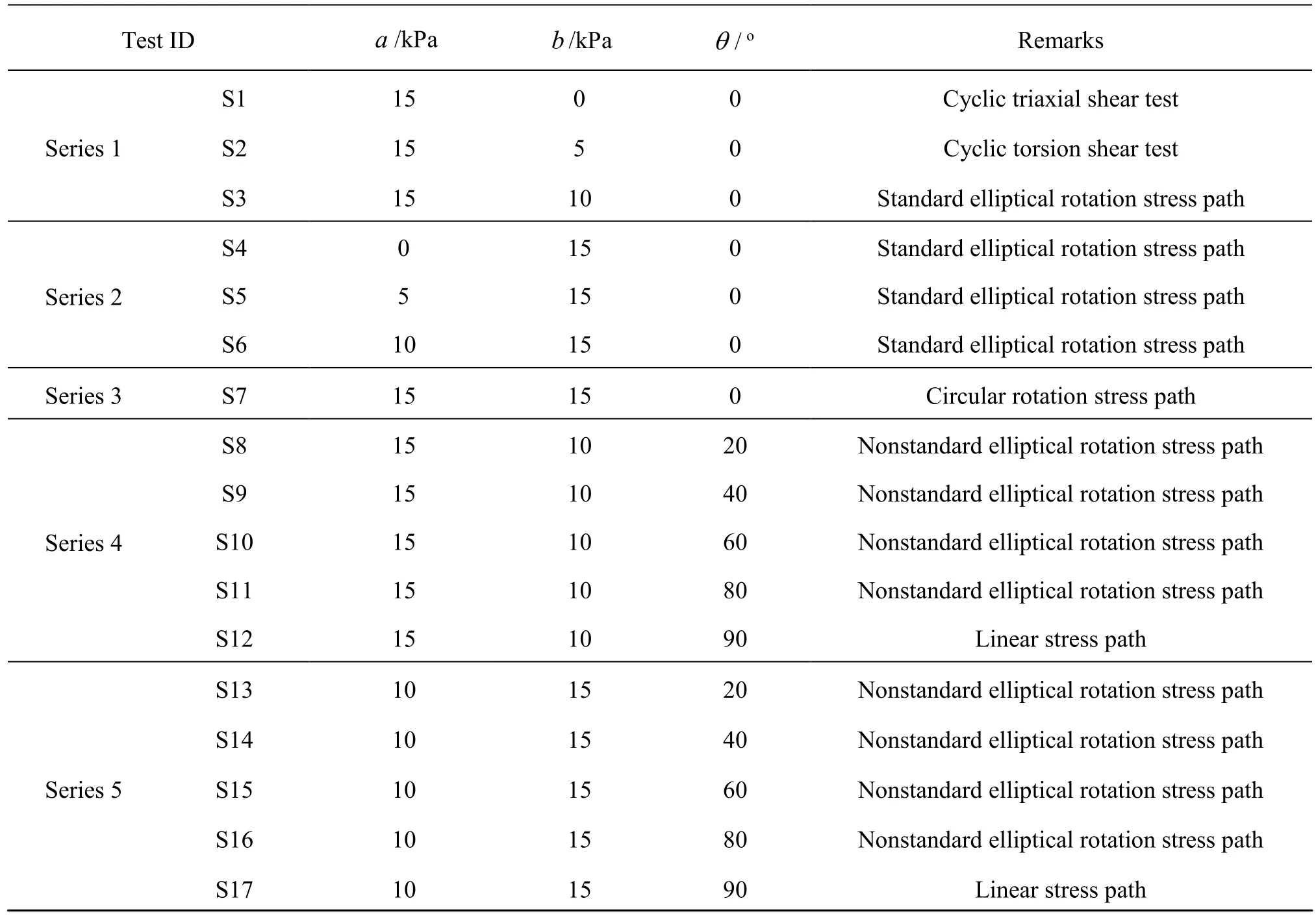
Table 3 Tests in detail

2.2Test programme

Firstly, a comparison of the experimental results between the circular stress path and the elliptical stress path is made to demonstrate the necessity of adopting the elliptical rotation stress path to evaluate the cyclic strength of the sand in the finite seabed. Secondly, seventeen hollow cylinder triaxial-torsional tests are carried out to explore the relationship betweenNfand the three parametersa,bandθfor the nonstandard elliptical rotation stress path.

2.2.1 Comparative tests between the circular rotation stress path and the elliptical rotation stress path Six hollow cylinder triaxial-torsional tests are conducted to demonstrate the difference of the cyclic strength between the elliptical rotation stress path and the circular rotation stress path. The stress paths are correspondingly inferred from the analytical solutions for the finite and infinite seabeds at the depths ofz/h=−0.16, −0.24, −0.32 of the example in Section 1.The calculated values ofa,bandθare listed in Table 2 together with the experimental values.

2.2.2 Tests for the nonstandard elliptical rotation stress path

Seventeen hollow cylinder triaxial-torsional tests are carried out to see the effect of the nonstandard elliptical rotation stress path on the cyclic strength. In Section 1, it is shown thata,bandθare three key parameters that determine the size and the shape of a nonstandard ellipse. Therefore, in this part, by fixing two of them and changing the other, some shear characteristics for a nonstandard elliptical rotation stress path can be found. Three parametersa,bandθare designed to cover the major range of the shear stress, the normal stress difference and the initial phase difference for the example in Section 1.

The program for the cyclic rotational shear test is as follows:

(1) Series 1: fixaand keepθ=0, changeb(a＞b).

(2) Series 2: fixband keepθ=0, changea(a＜b).

(3) Series 3:a=b,θ=0.

(4) Series 4: fixbanda, changeθ(a＞b).

(5) Series 5: fixaandb, changeθ(a＜b).

The tests are summarised in Table 3 in detail.

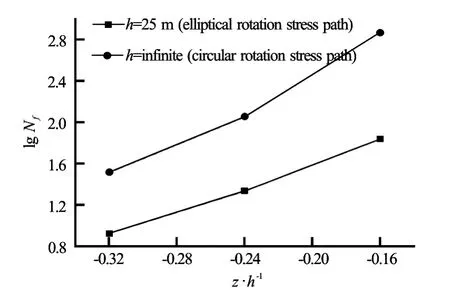
Fig.3 Comparison between the elliptical rotation stress path and the circular rotation stress path

2.3Test results and analyses

2.3.1 The results of the comparative tests between the circular rotation stress path and the elliptical rotation stress path

The results of the failure cycles for varying positions of the seabed under the elliptical rotation stress path and the circular rotation stress path are shown in Fig.3. The failure cycles for the latter are increased when the thickness of the seabed tends to infinite, which indicates that the stress strength induced by the wave loading may be underestimated if the finite seabed is regarded as infinite. Therefore, the shear characteristics under the circular rotation stress path in the literature are not applicable for analyzing the cyclic strength of the sand in the finite seabed.

2.3.2 The effect of the nonstandard elliptical rotation

stress path

The experimental results in Section 2.2.2 are plotted in Fig.4 and Fig.5. Figure 4 shows the relationship between the minor part (aorb) and lgNfwhen the major part (bora) is fixed to be 15 kPa andθ=0, indicating that:

(1)lgNfdecreases as the minor part increases.

Fig.4 The relationship between the minor part (aorb) and lgNf

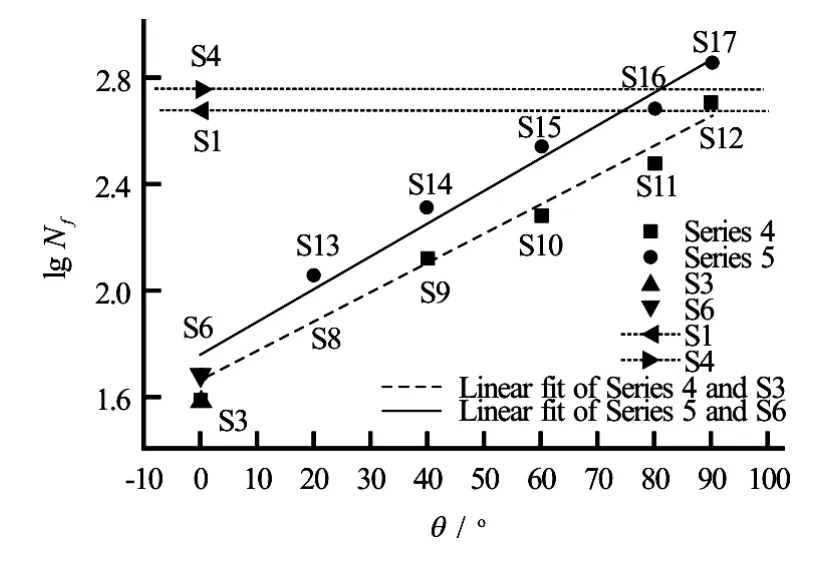
Fig.5 The relationship betweenθandNf

Figure 5 shows the test results of Series 4 and Series 5. The results of S3 and S6 are also plotted to show the relationship between lgNfandθ. The results of S1 and S4 are also evaluated. From Fig.5, it follows that:

(1)lgNfandθdisplay an approximately linear relation for specimens with the sameaandb, andlgNfincreases withθrapidly, which means that the influence ofθon the cyclic strength is significant.

(2) By comparing every pair of Series 4 and Series 5 like S13 and S8, at a givenθ,lgNfof Series 5 is larger than that of Series 4, as is consistent with the experimental results of Fig.4.

(3) Due to the influence ofθ, it is uncertain that the cyclic strength under the nonstandard elliptical rotation stress path is larger or smaller than that of the cyclic triaxial shear test or the cyclic torsion shear test (for example, the results of S1, S4, S6, S17).

3. Conclusion

The wave-in duced stress path in the seabed is traditionally considered as a circle. However, the circular rotation stress path only occurs in an infinite seabed. In this paper, a nonstandard elliptical rotation stress path is shown to be a more common stress state based on the analytical solutions for a finite seabed. Three parametersa,bandθrelated to the size and the shape of the ellipse are considered. An experimental comparison between the circular stress path and the elliptical stress path is conducted and the experimental results demonstrate the necessity of adopting the elliptical rotation stress path to evaluate the cyclic strength of the sand in a finite seabed. Then the cyclic strength under the nonstandard elliptical rotation stress path is investigated in more detail by seventeen hollow cylinder triaxial-torsional tests. The experimental results indicate that the cyclic strength under the nonstandard elliptical rotation stress path is evidently more complex and diversified as compared with a circular rotation stress path or a cyclic triaxial or torsion shear test. Especially the cyclic strength increases with the increase of the initial phase differenceθrapidly, which means that the influence ofθshould be paid more attention. The experimental observations in this paper might be used to establish a new failure criterion for the nonstandard elliptical rotation stress path.

[1] Madsen O. S. Wave-induced pore pressures and effective stresses in a porous bed [J].Géotechnique, 1978, 28(4): 377-393.

[2] Ishihara K., Towhata I. Sand response to cyclic rotation of principal stress directions as induced by wave loads [J].Soils and Foundations, 1983, 23(4): 11-26.

[3] Yang Z. X., Li X. S., Yang J. Undrained anisotropy and rotational shear in granular soil [J].Géotechnique, 2007, 57(4): 371-384.

[4] Lade P. V., Rodriguez N. M., Dyck E. J. V. Effects of principal stress directions on 3D failure conditions in cross-anisotropic sand [J].Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(2): 362-363.

[5] Rodriguez N. M., Lade P. V. Effects of principal stress directions and mean normal stress on failure criterion for cross-anisotropic sand [J].Journal of Engineering Mechanics, 2013, 139(11): 1592-1601.

[6] Kuenza K., Towhata I., Orense R. P. et al. Undrained torsional shear tests on gravelly soils [J].Landslides, 2004, 1(3): 185-194.

[7] Georgiannou V. N., Konstadinou M. Cyclic behaviour of loose anisotropically consolidated Ottawa sand under undrained torsional loading [J].Géotechnique, 2013, 63(13): 1144-1158.

[8] Blanc M., Benedetto H. D., Tiouajni S. Deformation Charcteristics of dry hostun sand with principal stress axes rotation [J].Soils and Foundations, 2011, 51(4): 749-760.

[9] Xiao J., Juang C. H., Wei K. et al. Effects of principal stress rotation on the cumulative deformation of normally consolidated soft clay under subway traffic loading [J].Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(4): 80-90.

[10] Graebe P. J., Clayton C. R. I. Effects of principal stress rotation on resilient behavior in rail track foundations [J].Journal of Geotechnical Engineering, 2014, 140(2): 1-10.

[11] Yu H. S., Yang L. T., Li X. et al. Experimental investigation on the deformation characteristics of granular materials under drained rotational shear [J].Geomechanics and Geoengineering, 2015, 11(1): 47-63.

[12] Konstadinou M., Georgiannou V. N. Effects of density on cyclic behaviour of anisotropically consolidated Ottawa sand under undrained torsional loading [J].Géotechnique, 2014, 64(4): 287-302.

[13] Pan H. Undrained dynamic strength behavior of saturated nanjing fine sand under wave load [J].Marine Georesources and Geotechnology, 2016, 34(2): 188-193.

[14] Hsu J. R. C., Jeng D. S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness [J].International Journal for Numerical and Analytical Methods in Geomechanics, 1994, 18(11): 785-807.

[15] Lee T. C., Tsai C. P., Jeng D. S. Ocean waves propagating over a porous seabed of finite thickness [J].Ocean Engineering, 2002, 29(01): 1577-1601.

[16] Liu Z., Jeng D. S., Chan A. H. C. et al. Wave-induced progressive liquefaction in a poro-elastoplastic seabed: A two-layered model [J].International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(5): 591-610.

[17] Hua L. N., YU X. P. Element-free Galerkin method for response of stratified seabed under wave action[J].Journal of Hydrodynamics, 2009, 21(4): 550-556.

[18] Sun Y. J., Lu S. Q., Lin W. Q. et al. In-situ study on nutrient release fluxes from shallow lake sediments under wind-driven waves [J].Journal of Hydrodynamics, 2016, 28(2): 247-254.

[19] Zhao H. Y., Jeng D. S., Guo Z. et al. Two-dimensional model for pore pressure accumulations in the vicinity of a buried pipeline [J].Journal of Offshore Mechanics and Arctic Engineering, 2014, 136(4): 042001.

[20] Zhang Y., Jeng D. S., Gao F. P. et al. An analytical solution for response of a porous seabed to combined wave and current loading [J].Ocean Engineering, 2013, 57: 240-247.

[21] Zhou X., Zhang J., Wang J. et al. Stability and liquefaction analysis of porous seabed subjected to cnoidal wave [J].Applied Ocean Research, 2014, 48: 250-265.

[22] Wang Z. T., Liu P., Yang Q. Dynamic strength of saturated loose sand under nonstandard elliptical stress path [J].Chinese Journal of Geotechnical Engineering, 2016 38(6): 1133-1139(in Chinese).

* Project supported by the Natural Science Foundation of China (Grant Nos. 51639002, 51209033), the Specialized Research Fund for the Doctoral Program of Higher Education (Grant No. 20120041130002).

Biography:Zhong-tao Wang (1974-), Male, Ph. D., Associate Professor

Peng Liu, E-mail:lp-536@163.com