Active thermophoresis and diffusiophoresis

Huan Liang(梁欢) Peng Liu(刘鹏) Fangfu Ye(叶方富) and Mingcheng Yang(杨明成)

1Beijing National Laboratory for Condensed Matter Physics and CAS Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences(CAS),Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3Wenzhou Institute,University of Chinese Academy of Sciences,Wenzhou 325001,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: active matter,colloid,thermophoresis,diffusiophoresis

1. Introduction

Active matter consists of self-propelled units that are capable of individually converting ambient energy into their locomotion.[1–3]Due to inherently out-of-equilibrium feature,active matter systems often exhibit exotic nonequilibrium phenomena not found in passive systems,including complex collective motions,[4–9]motility-induced phase separation,[10,11]abnormal rheology,[12]and thermodynamics.[13–15]In spite of the fundamental differences between active and passive systems, the basic thermodynamic concepts in passive systems have been widely extended and studied in active systems, which has significantly advanced our understanding of nonequilibrium properties of active matter. For instance,except for the case of active Brownian particles, the mechanical pressure of active systems is usually not a state quantity,[13,16,17]in stark contrast to equilibrium systems. The depletion interaction in equilibrium colloids[18]has also been conceptually generalized to the active bath,[19–22]and the effective interaction between passive particles in the active bath substantially depends on an external constraint suffered by the passive particles.[23]Additionally,in general,the effective temperature in the active bath cannot be uniquely defined,and different physical processes often correspond to different effective temperatures.[24–26]

Besides the basic thermodynamic quantities mentioned above,it is desirable to extend nonequilibrium thermodynamic concepts, usually discussed in the linear response regime of passive systems, to the active bath. Phoresis is one typical representative of such concepts, and it refers to the directed migration of suspended particles in a passive solution with an external gradient field.[27]Paradigmatic examples include thermophoresis,[28,29]diffusiophoresis,[30,31]and electrophoresis,[32]whose driving fields respectively correspond to the gradients of temperature,solute concentration and electric potential. The passive phoretic effects have been extensively applied to control mesoscale objects[33–35]and to design self-propelled particles,[36–42]in which the required gradient fields are self-generated.

In a very recent theoretical work,[43]the concept of phoresis has been extended from passive to active systems. Specifically,the passive solvent with an externally applied thermal or chemical gradient is replaced by a fluid of ideal active Brownian particles with a spatially nonuniform activity or concentration. In this inhomogeneous active bath, a suspended passive particle is shown to drift against the gradient of the activity or concentration, reminiscent of the passive phoresis. Actually,the directed transport of passive objects in an active bath with an activity gradient has been investigated in earlier theoretical and simulation work,[44–46]although the similarity to phoresis was not discussed and the concept of active phoresis was not put forward. This inhomogeneous activity-induced transport of passive objects has even been exploited to explain the experimental observation that the spontaneous movement of the nucleus from the cortex to the center of the oocyte cell,[47]where the activity of intracellular molecular motors is assumed to be position-dependent. However,most of these studies[43–45]only consider an ideal active bath composed of noninteracting self-propelled particles. On the other hand,although the active particles in Ref. [46] are nonideal, directed transport only occurs for attractive couplings between the active particle and passive objects due to special system settings,different from the results in Refs.[43–45]. So,it is interesting to study the active phoresis of a passive particle in inhomogeneous nonideal active baths,particularly with purely repulsive interactions between the active and passive particles.

In the present work, we perform simulations to systematically study the active thermophoresis and diffusiophoresis of a passive colloidal object immersed in inhomogeneous active baths. Distinct from previous works, we consider a nonideal active bath composed of interacting active Brownian particles (ABPs) that couple with the passive colloid through a purely repulsive potential. Our results show that the interactions between the “solvent” particles have a great impact on the active phoretic effects. Particularly, the active thermophoretic drift can change the direction with the activity gradient of the ABPs, and the active diffusiophoretic motion is always along the concentration gradient of the ABPs, in contrast to the case of the active phoresis in ideal active baths.The results can be rationalized by analyzing the osmotic pressure and concentration distribution of the solvent particles.Moreover,we quantify the active thremophoretic and diffusiophoretic forces experienced by frozen passive colloidal particles and the thermoosmotic-like flow of the ABPs induced by the passive colloidal particle. The findings are reminiscent of the scenario of passive phoresis, further suggesting the concept of phoresis can be extended to active bath.

2. Simulation method and system

We consider a two-dimensional system with periodic boundary conditions in thexandydirections. The inhomogeneity of the active bath is prescribed in thexdirection, as sketched in Figs. 1(a) and 1(c). In the thermophoretic situation, the system is composed of small active Brownian particles (ABPs) of diameterσand a large passive colloidal particle of diameter 3σin a rectangular box of the dimensionsx0×y0(x0= 2y0andx0≥46σ), with the mean packing fraction ¯ρ. The ABPs are subjected to a linearly positiondependent self-propelling forceFd(x) [Fig. 1(a)], which corresponds to a nonuniform effective temperature of the active bath.Because of the periodic boundary conditions,Fd(x)has a symmetric profile,with the maximum valueFmdon the boundary and the vanishing magnitude in the middle of the system.The interactions between different ABPs and between the active and passive particles are taken as the repulsive Lennard–Jones-type potential,U(r)=4ε[(σ/r)24-(σ/r)12]+εifr ＜21/12σ, andU(r)=0 otherwise. The dynamics of the ABPs obeys the overdamped Langevin equations,

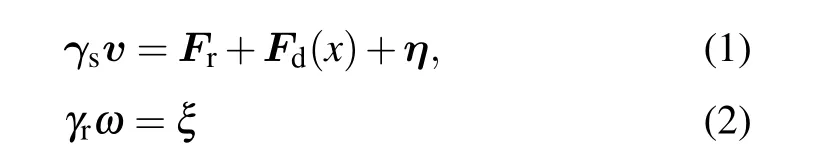
withFrthe static force on the ABP, andγs=100 andγr=γsσ2/3 being the translational and rotational friction coefficients,respectively. Here,ηandξare separately the stochastic force and torque from the thermal bath, which are Gaussian distributed with zero mean and variance〈ηi(t)ηj(t′)〉=2kBTγsδijδ(t-t′)and〈ξ(t)ξ(t′)〉=2kBTγrδ(t-t′),with the temperaturekBT=ε=1. The dynamics of the passive colloidal object evolves similarly according to Eq. (1) but withFd=0 and the translational friction coefficientγl=3γs.

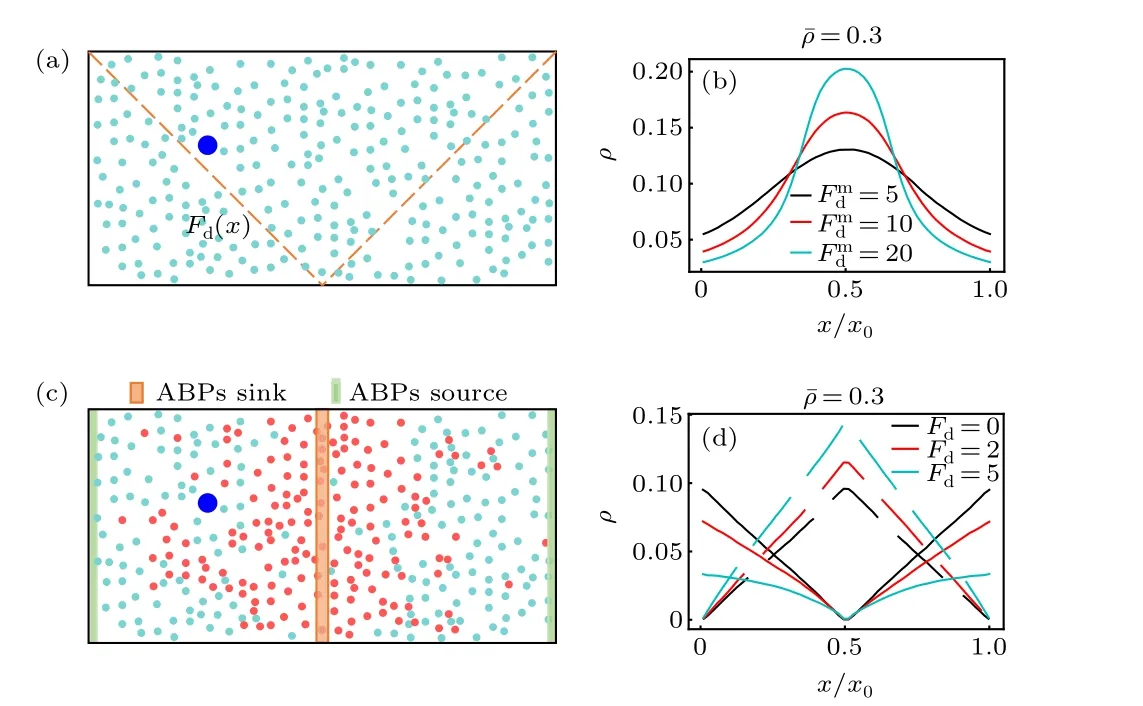
Fig. 1. (a) Schematic diagram of thermophoretic system. A large passive colloidal particle(large blue circle)is immersed in a fluid of the ABPs(small cyan circle)experiencing a linearly position-dependent activity Fd(x)represented by the dashed line. (b) The steady-state density distribution of the ABPs in the thermophoretic system with ¯ρ =0.3, for different gradients of the self-propelling force (i.e., Fmd ). (c) Sketch of diffusiophoretic system,in which a large passive colloidal particle(large blue circle)is suspended in a fluid mixture composed of small passive particles (red circle) and ABPs.Here, the sink and source of the ABPs are located in the system center and boundary regions, respectively. (d) The density distribtutions of the small passive particles (dashed line) and ABPs (solid line) in the diffusiophoretic system with ¯ρ =0.3 and Pr=1.0,for different Fd exerted on the ABPs.

In the diffusiophoretic system, the “solvent” is a mixture consisting of small passive particles and ABPs experiencing a constantFd, as sketched in Fig. 1(c), unlike the singlecomponent active systems in the theoretical work.[43]To establish a stationary concentration gradient of ABPs, the sink and source of the ABPs are imposed separately in the middle and boundary regions of the simulation system. Specifically,when a solvent particle moves into the middle region, it will transform into a small passive(active)particle with the probabilityPr(1-Pr); while, a reverse operation is performed in the boundary region of the system. Such artificial chemical reactions can quickly generate a steady-state concentration gradient of the ABPs as well as the small passive particles. It should be noted that this binary-component solvent(except the background thermal bath)is employed in order to naturally achieve a steady-state gradient of the ABPs. This setup follows the idea usually used in the simulation of passive diffusiophoresis,[48,49]since,otherwise,a density gradient of single-component solvent will inevitably induce a macroscopic pressure gradient.Different solvent particles(including the small passive and active particles)interact with each other via the same repulsive Lennard–Jones-type potential. Similar to the thermophoretic case,the motions of the solvent particles and the big passive colloidal particle are described by the overdamped Langevin equations. Here, the small passive solvent particles have the same translational friction coefficientγsas the ABP and a vanishingFd.

3. Results and discussion

3.1. Density distribution of the“solvent”particles

Before the investigation of the active phoresis, we measure the steady-state density distribution of the solvent particles in the nonuniform environment in the absence of the big passive colloidal object. Figure 1(b) plots the concentration of the ABPs as a function of thexcoordinate in the thermophoretic systems. In this case, the position-dependent activity induces a spatially inhomogeneous distribution of the active particles that prefer to accumulate in the region of low activity(namely in the middle of the system),consistent with previous work.[50–52]Since the activity gradient is symmetric with respect to the system center, the density distribution of the ABPs also has a symmetric profile. Further, when the mean packing fraction of the ABPs remains fixed ¯ρ=0.3,the inhomogeneity of the ABP concentration increases as the activity gradient(i.e.,Fmd)enhances.

In the diffusiophoretic case, the stationary concentration distributions of the ABPs and passive solvent particles almost linearly depend on thexcoordinate, as shown in Fig. 1(d).And, they have opposite trends, since, by construction, the source and sink of the ABPs respectively correspond to the sink and source of the passive solvent particles. Interestingly,when the mean packing fraction ¯ρand the reaction probabilityPrare constant,the density gradients of the ABPs and passive particles are dependent on the self-propelling force applied to the ABPs[Fig.1(d)]. With the rise ofFd,the density gradient of the ABPs decreases,while that of the passive solvent particles increases. This behavior can be understood based on the following fact. The ABP subjected to a strongFdhas a large effective diffusion coefficient, such that it more easily leaves its source region and enters its sink region at the system center,thus resulting in a flatter concentration profile of the ABPs.As a consequence, more ABPs transform into small passive particles,and the density gradient of the passive solvent particles becomes larger.

3.2. Active thermophoresis of passive colloidal particle in active bath

When a large passive colloidal particle is suspended in the active bath with a spatially varying activity, it will usually experience a directed drift parallel to the activity gradient,producing a nonuniform density distribution. This behavior is similar to the traditional thermophoresis in passive solutions.Figure 2(a)displays the probability distribution of the passive colloidal particle in the gradient direction for different maximum self-propelling forcesFmd. For smallFmd, the colloidal particle is inclined to move to the region of low activity (the center of the system) and exhibits a “thermophobic” motion;while, for largeFmd, it tends to accumulate in the region of high activity and behaves “thermophilically”. And, there exists a crossover between the thermophobic and thermophilic motions as theFmdvaries.

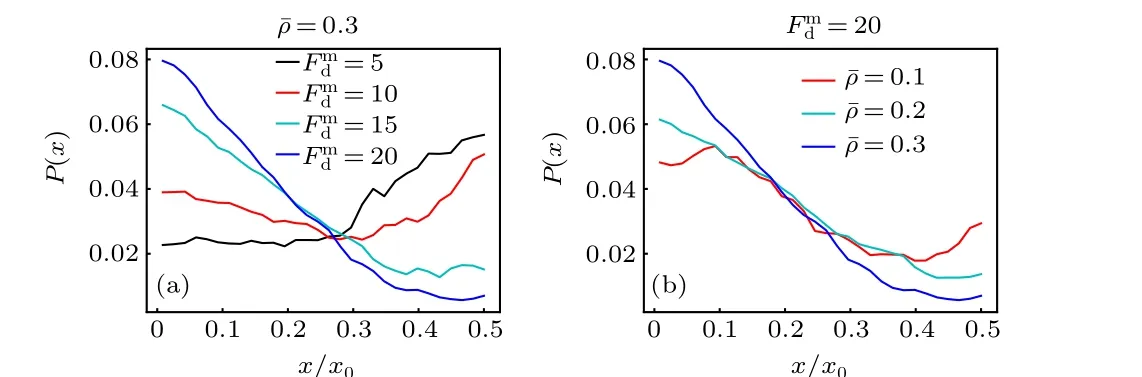
Fig. 2. Probability distribution of the large passive colloidal particle as a function of the x coordinate(a)for different Fmd with ¯ρ =0.3 fixed,and(b)for different mean packing fraction of the ABPs ¯ρ with Fmd =20 fixed.

Previous theoretical works[43,44]have predicted that the passive object immersed in an ideal active bath drifts against the activity gradient, since the high-activity area has a higher swimming pressure. This prediction is consistent with our results at smallFmd, but is opposite to those at largeFmd. This difference mainly arises from the fact that the active particles in our system are interacting(instead of ideal)ABPs and they occupy most space of the low-activity region for large enoughFmd[see Fig. 1(b)]. In this situation, the passive colloidal particle cannot easily enter the crowded low-activity region and thus accumulate near the system boundary (high activity). From the point of view of pressure, the Virial pressure contributed by the interparticle interactions overwhelms the swimming pressure in the crowded region. This thermophilic motion weakens with the decrease of the mean packing fraction of the ABPs, as shown in Fig. 2(b), since the crowding effect of the ABPs is weak at low ¯ρ. Moreover, the results above are also different from those obtained in the simulation study,[46]in which the attractive interactions between the passive colloid and active bath particles drive the colloid to drift towards the low-activity region, while the net drift vanishes for repulsive interactions owing to the special system settings.However,in our nonideal active baths,the passive colloid can transport both along and against the activity gradient,depending on the magnitude ofFmd. This highlights the importance of the excluded-volume interactions between the ABPs in the active thermophoresis.

To further investigate the active thermophoresis,we measure the driving force exerted on a frozen passive colloidal particle by the active bath. In the simulations, two identical colloidal particles are fixed separately at two symmetric positions,as displayed in Fig.3(b). Due to the symmetry,we only consider the left colloidal particle. Figure 3(a) indicates that the active thermophoretic forceFlargechanges nonmonotonically,with a direction reversal,as the activity gradient increases.For small and largeFmd,Flargepoints to the low-activity and highactivity regions,respectively. And,the magnitude ofFlargeincreases with the mean packing fraction of the ABPs[Fig.3(a)].These observations are consistent with the probability distribution of the passive colloidal particle in Fig. 2. It is well known that,for the passive thremophoresis,the reaction of the thermophoretic force on a fixed colloidal particle can induce a thermoosmotic flow of the surrounding solvent.[29,53,54]Similarly, it can be expected that there also exists a flow of active particles around the active thermophoretic object. Indeed,figure 3(b)illustrates such an osmotic flow in the opposite direction to the active thermophoretic force. Because of the system symmetry,the flow field has a symmetric pattern.

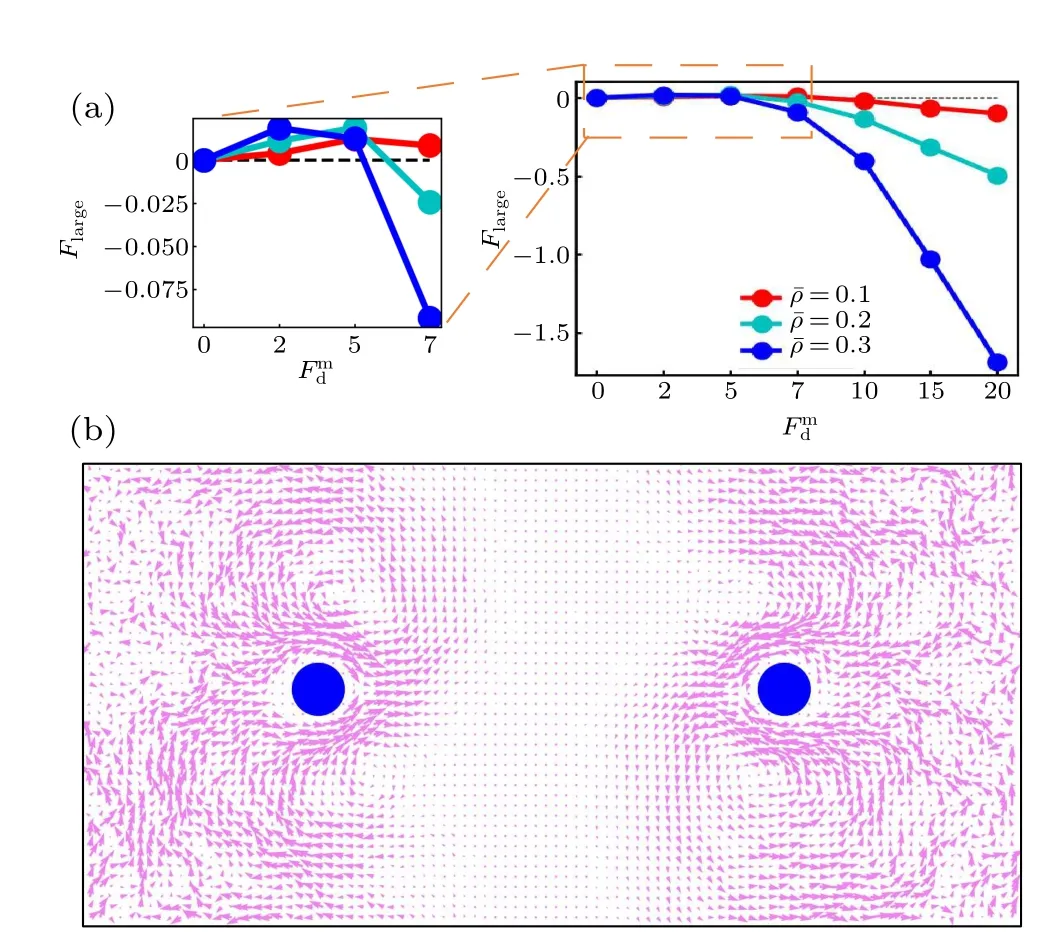
Fig. 3. (a) The active thermophoretic force on the passive colloidal particle frozen in the left half simulation box as a function of Fmd , for different¯ρ. The positive direction of Flarge points to the system center (namely thermophobic). Inset is an enlarged view of the active thermophoretic force for small values of Fmd .(b)The flow field of the ABPs induced by the reaction of Flarge exerted on the passive colloidal particle. Here, Flarge is negative, with Fmd =20 and ¯ρ =0.3.

Before closing this section,we study the position dependence of the active thermophoretic force. From Fig.1(b),the density profile of the ABPs is nonlinear, although the activity gradient is constant. This implies that the environmental inhomogeneity felt by the passive colloid hinges on its position,such thatFlargeis position-dependent. Figure 4 plots theFlargesuffered by the colloidal particle fixed at three different positions. It is clearly shown thatFlargechanges with itsxcoordinate (uniform in theydirection), meaning that the active thermophoretic accumulation of the colloidal particle is a consequence of the averageFlargein the present system.

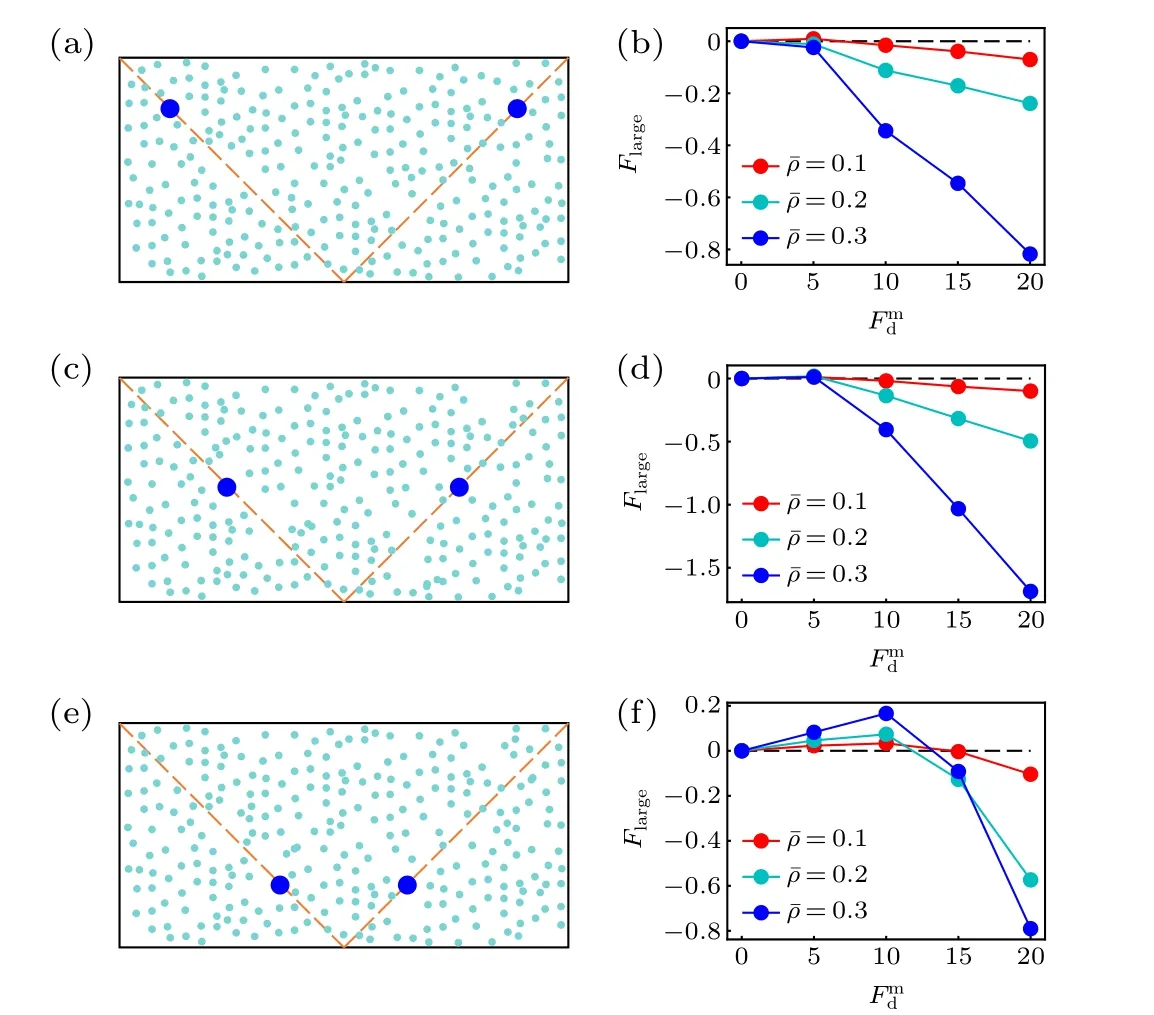
Fig.4. Sketch of two passive colloidal particles fixed in the nonuniform active bath,with their x coordinates separately(a)x1 = x0 and x2 = x0,(c)x1=x0 and x2=x0,(e)x1= x0 and x2= x0. [(b),(d),(f)]The active thermophoretic forces on the left frozen colloidal particles,which separately correspond to panels(a),(c),and(e).

3.3. Active diffusiophoresis of passive colloidal particle in active bath

Now we replace the activity gradient with a concentration gradient of the ABPs,and investigate the active diffusiophoresis of the passive colloidal particle in the mixture composed of active and passive solvent particles. Figure 5 displays the probability distribution of the large passive colloidal particle.Under the parameters under study,the passive colloid drifts to the source region of the ABPs(the system boundary)and accumulates there. The observation is opposite to the theoretical prediction of the previous work,[43]where the passive colloid in a single-component ideal active bath always moves to the low-concentration area of the ABPs. This difference can be explained as follows. For the single-component active bath,the density(thus osmotic pressure)of the active particles near the source is higher than near the sink region, which drives the passive colloid to drift towards the low-concentration region. While, for our present active-passive mixture bath, the solvent particles have a larger packing fraction close to the sink of the ABPs, as plotted in Fig. 1(d). Figures 5(a) and 5(b) also show that the accumulation of the passive colloidal particle monotonically increases separately with increasing the self-propelling force and the mean packing fraction.

Following the case of the active thermophoresis,we also quantify the active diffusiophoretic force on a passive colloidal particle fixed atx=x0/4, as plotted in Fig. 6. With the increase of the ABP activity and the packing fraction of the system, the magnitude ofFlargerises [Fig. 6(a)]. And, the active diffusiophoretic force is always along the concentration gradient of the ABPs. These results are consistent with the probability distribution of the colloidal particle in Fig. 5. In addition, the magnitude ofFlargebasically enhances with the transition probabilityPr[Fig. 6(b)], since a largerPrcauses a higher concentration gradient. As the active diffusiophoretic force in the present system is relatively small,its resulted diffusioosmitc flow is weak and is not provided here. Finally,we study the position dependence of the active diffusiophoretic force by changing the position of the passive colloidal particle. In contrast to the active thermophoretic case, the active diffusiophoretic force on the colloidal particle is hardly dependent on its distance from the ABP source, as displayed in Fig. 7. This is because the density profiles of the ABPs and passive solvent particles are almost linear [see Fig. 1(d)]. In other word,the environmental inhomogeneity experienced by the passive colloidal particle is almost constant throughout the system(except for the areas close to the sink and source).

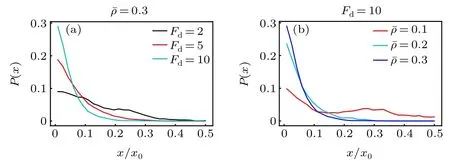
Fig.5.Probability distribution of the active diffusiophoretic passive colloidal particle (a) for different self-propelling force Fd and (b) for different mean packing fractions of the solvent particles ¯ρ,with Pr=1.0 being fixed.

Fig.6. The active diffusiophoretic force on the frozen passive colloidal particle as a function of(a)the self-propelling force for different ¯ρ with Pr=1.0 and(b)the transition probability Pr for different Fd. Here,the positive direction of the force points to the sink of the ABPs(the system center).

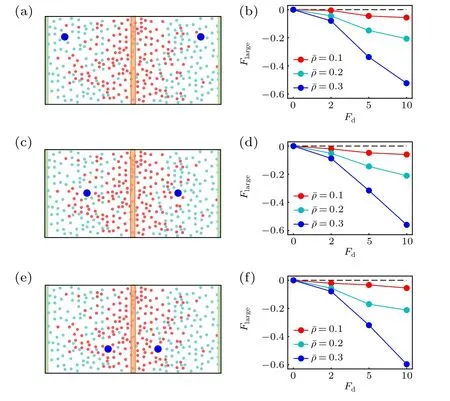
Fig. 7. Sketch of two active diffusiophoretic colloidal particles fixed in the nonuniform active bath,with their x coordinates separately(a)x1=0 and x2 =x0,(c)x1 =x0 and x2 =0,(e)x1 = and x2 = 0. [(b),(d),(f)] The active diffusiophoretic forces on the left colloidal particles, which respectively correspond to panels (a), (c), and (e). In the simulations, the transition probability Pr=1.0 remains fixed.

Although the active diffusiophoresis is obtained by imposing a steady-state constant concentration gradient, a similar behavior could be expected to happen in a dynamic gradient field. A recent theoretical study shows that a spatially local, and temporally abrupt change in fluid particle density may give rise to a diffusiophoretic-type motion of immersed inclusions.[55]

4. Conclusion

In the work,we numerically demonstrated that the passive colloidal particle exhibits phoretic-like motions in nonuniform nonideal active fluids. In the active bath consisting of the ABPs with a spatially varying activity,corresponding to an effective temperature gradient, the suspended passive colloidal particle suffers from a thermophoretic-like force and thus unidirectionally drifts parallel to the gradient. In the active fluid of the active-passive solvent mixture having a concentration gradient of the ABPs, the passive colloidal particle experiences a diffusiophoretic-like force and hence directed motion. The active thermophoresis and diffusiophoresis sensitively hinge on the imposed external gradients and the activity and packing fraction of the solvent particles, and even reverse the direction.Our results are largely different from those predicted by the previous theoretical work with ideal active baths,[43,44]which highlights the important role of the interactions between the solvent particles in the active phoresis. The phoretic-like transport and accompanying phoretic osmoticlike flow could be used to manipulate mesoscopic particles and to understand the tracer transport in living cells.[56,57]Our findings,particularly the active thermophoresis,would be easily verified by considering a colloidal particle in a bacterial solution with a spatially varying activity.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 11874397) and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB33000000).