On d-Dimensional Lattice(co)sine n-Algebra∗
Shao-Kui Yao(姚少魁),Lu Ding(丁璐),Peng Liu(刘鹏),Chun-Hong Zhang(张春红), and Wei-Zhong Zhao(赵伟忠),
1School of Mathematical Sciences,Capital Normal University,Beijing 100048,China
2Institute of Applied Mathematics,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China
3National Center for Mathematics and Interdisciplinary Sciences,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China
1 Introduction
In finite-dimensional algebra plays an important role in physics.As two important in finite-dimensional algebras,thew∞and SDi ff(T2)algebras have received considerable attention. They are the algebras of smooth area-preserving di ff eomorphisms of the cylinderS1×R1[1]and torusT2,[2−3]respectively. The general algebra of di ff eomorphisms of theN-torus has also been constructed.[4]The sine algebra is a kind of in finitedimensional algebras.[5−6]It arises as the unique Lie algebra deformation of SDi ff(T2)in some suitable basis.It should be pointed out that this sine algebra is indexed by a two-dimensional integer lattice.The generalized sine algebra which is indexed by thed-dimensional integer lattice has also been presented.[6]It was found that the problem of Bloch electrons in a constant uniform magnetic field admits the sine algebra as the symmetry algebra.[7]Moreover the sine algebra has the important applications in the quantum Hall effects.[8]
3-algebra has been paid great attention due to a world-volume description of multiple M2-branes proposed by Bagger and Lambert[9−10]and Gustavsson.[11]Recently one has also made an attempt of studying its applications in integrable systems[12−14]and condensed matter physics.[15−19]Some in finite-dimensional Nambu 3-algebras which satisfy the fundamental identity(FI)have been well constructed,such as Virasoro–Witt 3-algebra,[20−21](super)w∞3-algebra[22−23]and SDi ff(T3)3-algebra.[24]It should be mentioned the fiis not an operator identity.It holds only in special circumstances.Dinget al.[25]investigated the(co)sinen-algebra,where the generators are indexed by the 2-dimensional integer lattice.They constructed a sine 3-algebra which is a Nambu 3-algebra.Recentlyn-algebra has attracted great interest in condensed matter physics,since there are the close relations between quantum Nambu bracket in even dimensions andA-class topological insulator.[15]In this paper,we shall present a realization of the sine algebra,which is indexed by thed-dimensional integer lattice and derive the corresponding generalized(co)sinen-algebra.The properties of thisd-dimensional lattice(co)sinen-algebra including the limiting case will be analyzed.
2 Sine 3-algebra
Let us take the differential operators

whereαis a real parameter andNote that the differential operators we introduce here are indexed by a two-dimensional integer latticem=(m1,m2).
Using Baker–Cambell–Hausdorf formula

wherewe obtain that the commutation relation of the generators(1)is

where
The in finite dimensional sine algebra(3)has the important applications in physics.Dereli and Vermin[7]considered the following magnetic translation operators:
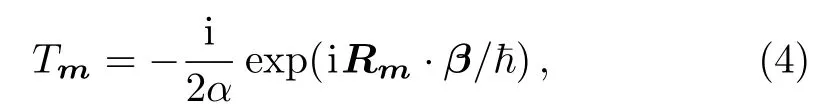
whereRm=m1a1+m2a2is an arbitrary Bravais lattice vector,β=(β1,β2)is a vector which is classically connected with the cyclotron center.In terms of the magnetic translation operators(4),they gave an explicit physical realization of the sine algebra(3).
In the limit(3)becomes
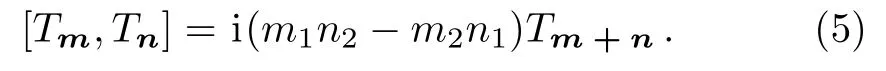
The in finite-dimensional algebra(5)is isomorphic to the centerless algebra of area-preserving di ff eomorphisms on the torus,i.e.,the SDi ff(T2)algebra.[2−3]
Let us now turn our attention to the case of 3-algebra.The operator Nambu 3-bracket is defined by[26]
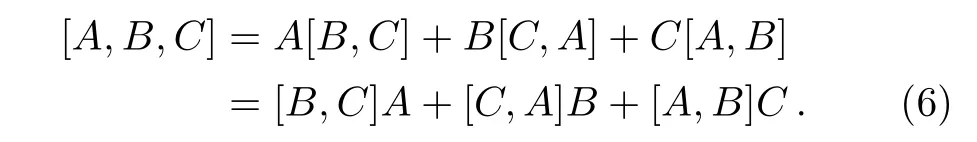
Substituting the generators(1)into the operator Nambu 3-bracket(6),we obtain the sine 3-algebra
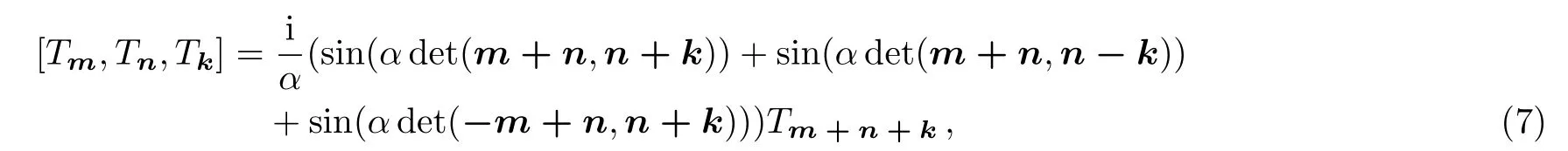
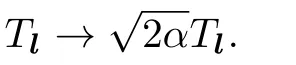
It was found that whenα=π/2,the sine 3-algebra(7)satisfies the FI[25]
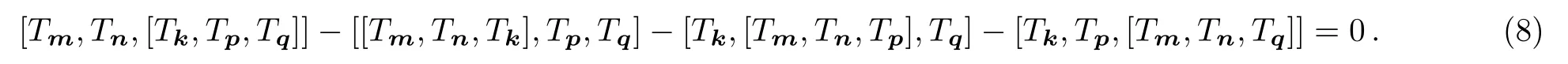
Taking the limitα→0 in(7),we obtain the 3-algebra[12]
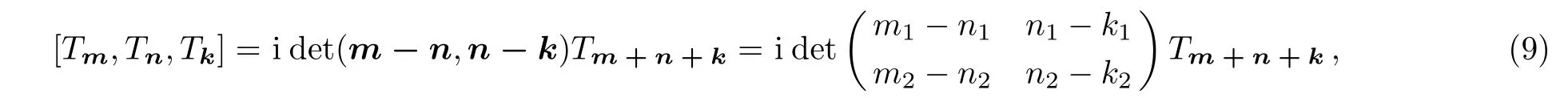
which also satisfies the FI(8).
As the generalized case of(1),let us take the following generators:
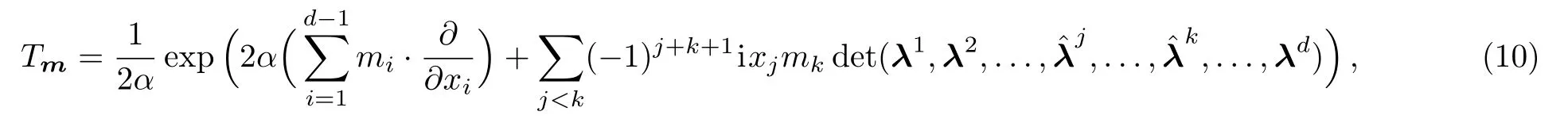
where the vectodenotes thed-dimensional integer lattice,i.e.,the parameter vectorsHere we denote a notational convention used frequently in the rest of this paper.Namely for any arbitrary symbolβ,the hat symbolstands for the term that is omitted.
The commutation relation of(10)is
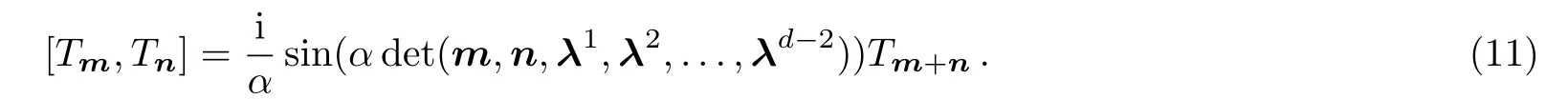
Since the generalized sine algebra(11)involves the operatorsTmwith indicesm=(m1,m2,...,md),we call(11)thed-dimensional lattice sine algebra.[6]
In the limitleads to the following in finite dimensional Lie algebra:

Whend=2,(12)gives the in finite-dimensional Lie algebra(5)which is isomorphic to the SDi ff(T2)algebra.[2−3]Substituting(10)into the quantum Nambu 3-bracket(6),we obtain thed-dimensional lattice sine 3-algebra
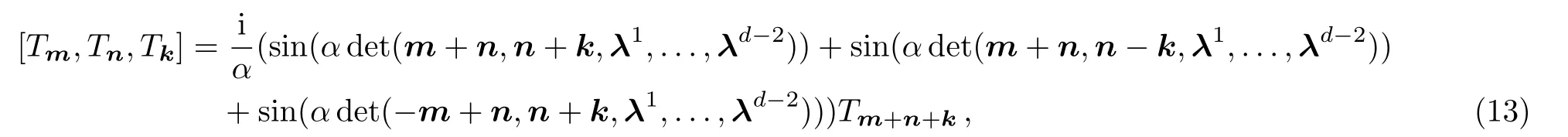

Let us consider the case of the special valueα=π/2 in(13).In this case,(13)becomes
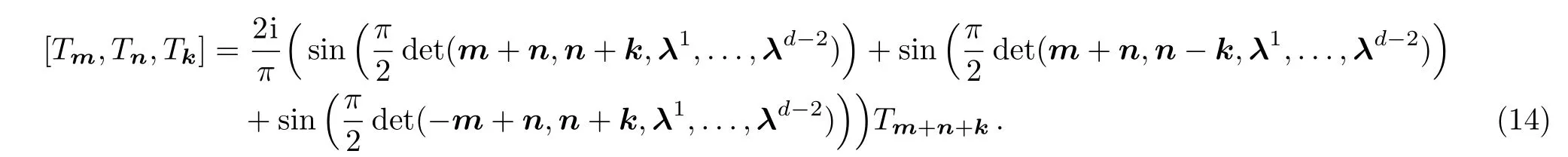
Whend=2,the sine 3-algebra(14)becomes(7)which satisfies the FI(8).We therefore proceed by investigating the arbitraryd-case.When the constantsare even,(14)is a null 3-algebra.Let us now focus on(14)by assuming that the constantis odd.By direct calculation,we find that(14)with any oddis actually equivalent to the case of.Thus in the following discussions,we takeinλd−2.
Suppose now that(14)satisfies the FI(8)for the case ofd−1.Corresponding to the generatorsTm(10),let us consider the following generators:

where
Substituting the generators(15)into the operator Nambu 3-bracket(6),we obtain
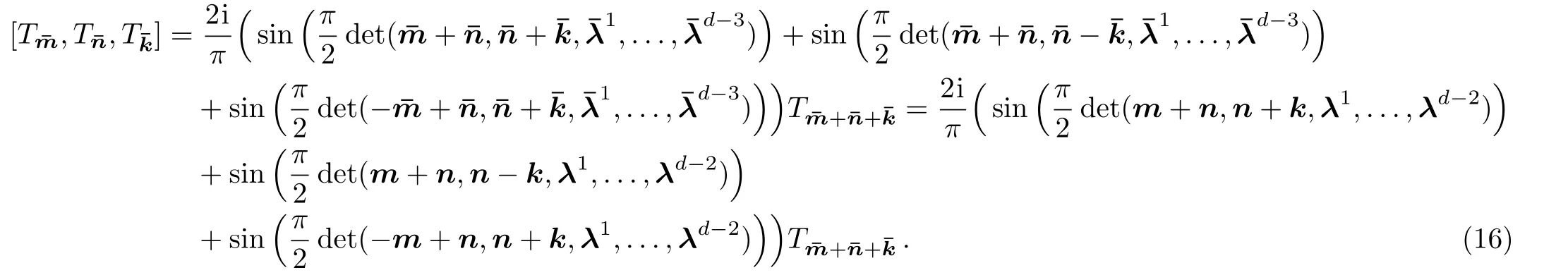
Not as the case of(14),(16)is a(d−1)-dimensional lattice sine 3-algebra.However it should be noted that there are the same structure constants for(14)and(16).Comparing with the each term in the left hand side of the FI(8)for thed−1 andd-dimensional lattice sine 3-algebras(14)and(16),a direct calculation shows that there are the same coefficients with respect to the generatorsand,respectively.Since the(d−1)-dimensional lattice sine 3-algebra(14)satisfies the FI(8),thed-dimensional lattice sine 3-algebra(16)necessarily satisfies the FI(8).It is obvious that the skew-symmetry holds for(14).Therefore we conclude that thed-dimensional lattice sine 3-algebra(14)is a Nambu 3-algebra.
In the limit(13)reduces to

By means of the following equality:

where,are the arbitrary constant vectors,it is easy to prove that the FI(8)holds for(17).Since the skew-symmetry also holds for(17),thus(17)is a Nambu 3-algebra.
As an example,let us consider the generators
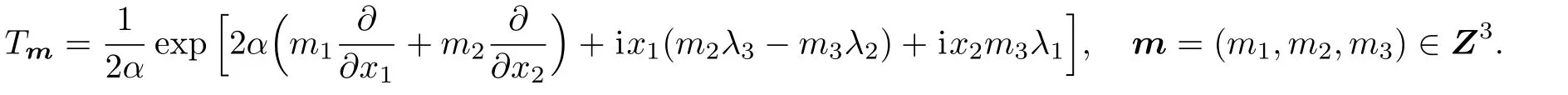
The corresponding Lie algebra and 3-algebra are

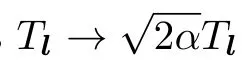
Let us take the limitin Eqs.(19)and(20),respectively.Then we have
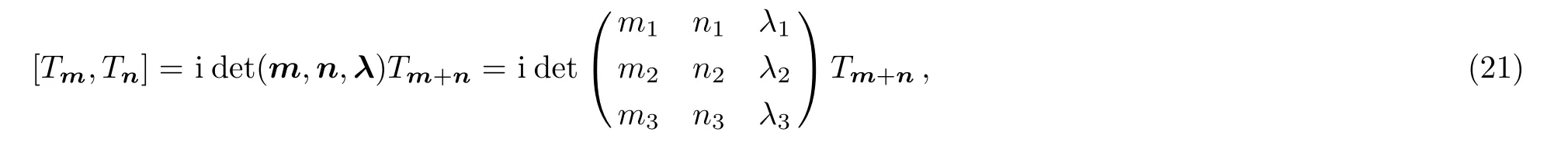

For the 3-torusT3,the periodic function basis are given by

whereandSubstituting(23)it into the Nambu 3-bracket
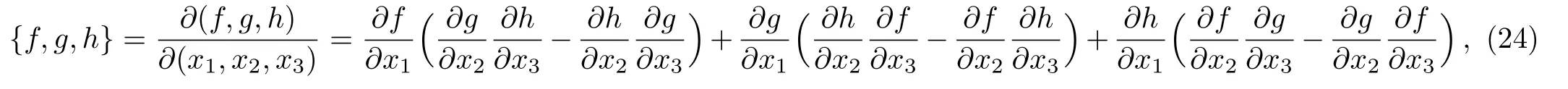
it leads to theT3Nambu–Poisson 3-algebra[24]

We have known that the algebra(5)is isomorphic to the centerless algebra of area-preserving diffeomorphisms on the torus.Comparing(22)with(25),we note that they are indeed the different 3-algebras.
3 Sinen-algebra
Then-bracket is defined by[27−28]

Since the generators(10)are the associative operators,(26)can be rewritten as

whereis the L´evi–Civit`a symbol,i.e.,
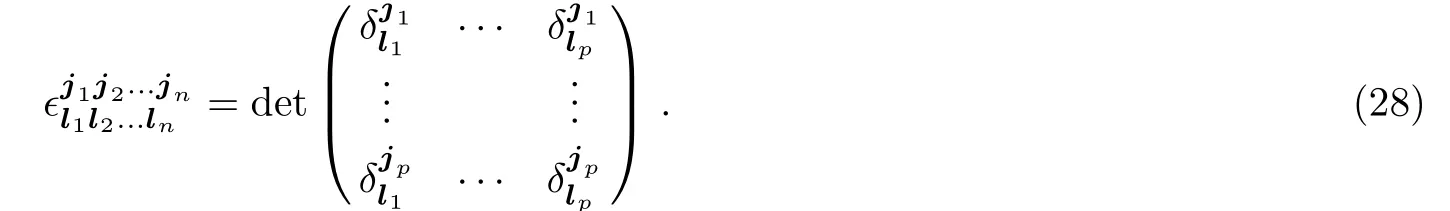
Based on(27),after a straightforward calculation,we obtain thed-dimensional lattice(co)sinen-algebra

where we take the scaled generatorsin then-bracket.In the limit of,we see that(29)gives a nulln-algebra for
For the Nambun-algebra,the corresponding fiis

Let us takeandPerforming straightforward calculations,we find that the left hand side of(30)is zero,however the right hand side is not.It implies that the FI(30)does not hold for then-algebra(29)with anyn.
In Ref.[27],it has been proved that whennis even,then-bracket with arbitrary associative operators satisfies the generalized Jacobi identity(GJI)

Due to the associative operatorsTm(10),we can con firm that then-algebra(29)withneven is a higher order Lie algebra.
As an example,let us consider thed-dimensional lattice cosine 4-algebra

whereIt is a higher order Lie algebra.
Whend=2,Eq.(32)gives the cosine 4-algebra derived in Ref.[25]
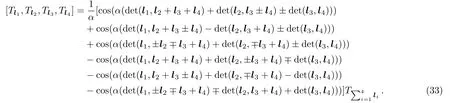
Whend=3,Eq.(32)becomes

Takingλ1=(0,0,1)in(34),we see that there are the same structure constants for(33)and(34).In the limit ofwe note that thed-dimensional lattice sine 3-algebra(13)gives a non-trivial Nambu 3-algebra.However the limiting case of(32)reduces to a null 4-algebra.
Let us turn to thenodd case in Eq.(31).In this case,the left hand of(31)can be rewritten as


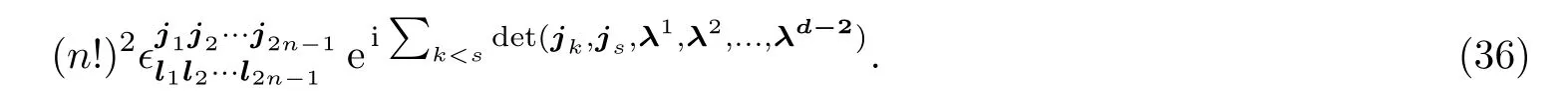


which does not equal zero.Therefore the GJI(31)does not hold for oddn.
Although thed-dimensional lattice(co)sinen-algebra(31)withnodd does not satisfy the the GJI(31),an interesting case is for the 2-dimensional lattice cosine 5-algebra with the special valueα=1/3

Dinget al.[25]found that the cosine 5-algebra(38)is a higher order Lie algebra.Inspired by this result,let us consider thed-dimensional lattice cosine 5-algebra with

Due to the skew-symmetry ofthe skew-symmetry holds for(39).By applying the mathematical induction,proceeding similarly as the case of(14),it is not hard to prove that(39)satisfies the GJI(31).Therefore theddimensional lattice cosine 5-algebra(39)is a higher order Lie algebra.
4 Super sinen-algebra
Let us take the following generators:
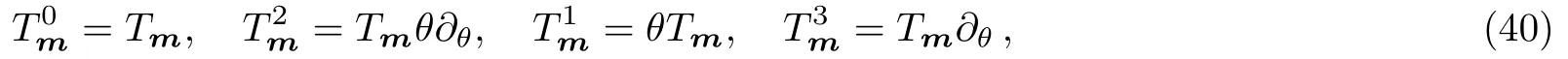
whereθis the fermionic variable,the parities of these generators are
The generators(40)form the super sine algebra
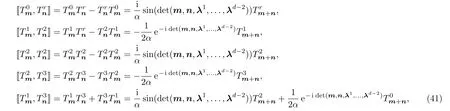
wherer=0,1,2,3.
The super multibracket of ordernis defined by[29]
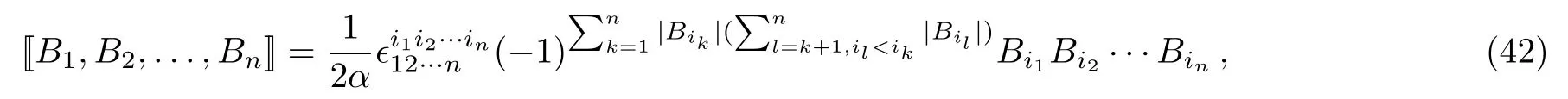
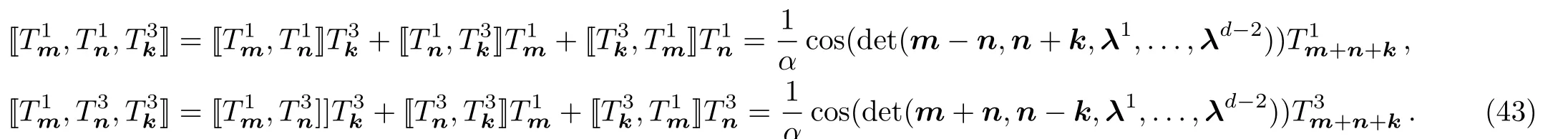
where|Bi|is the parity ofBi.
Substituting the operators(40)into(42),we obtain the super sine 3-algebra.Due to too many 3-algebra relations,we only list the fermionic 3-algebras that will be used in the later discussion
The super extensions of Nambu 3-algebra are of general interest.Recently Chenet al.[23]presented a super Nambu 3-algebra,i.e.superw∞3-algebra,which satisfies the super FI

Let us consider the super sine 3-algebra for the case ofα=π/2.In this case,we see that the bosonic 3-algebra(20)satisfies(44).However the super FI(44)fails for the fermionic 3-algebras(43).Thus for the special valueα=π/2,the generators(40)do not form the super Nambu 3-algebra.
Substituting the operators(40)into(42)and using the following product relations between the generators:
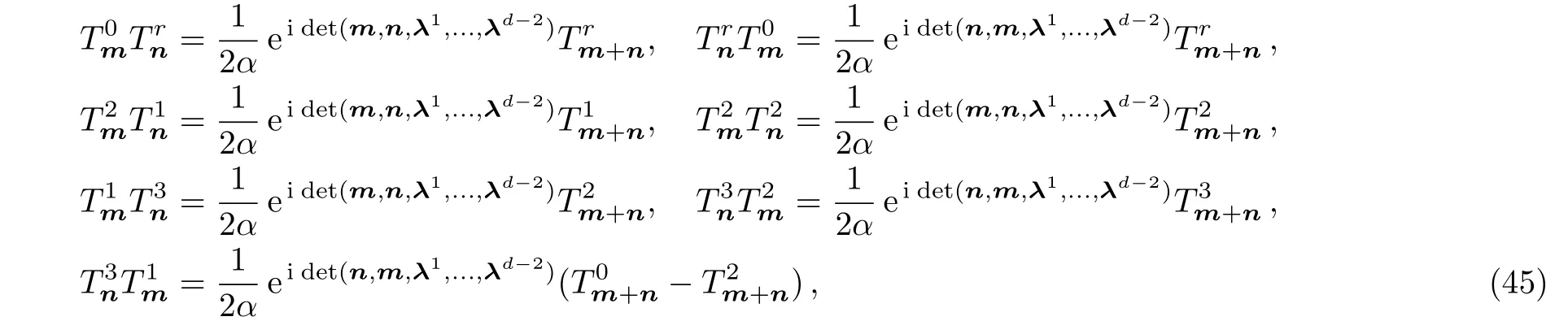
wherer=0,1,2,3,we may derive the super sinen-algebra

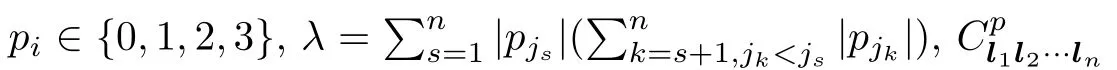
As an example,let us consider the super sine 4-algebra.Since there are too many 4-algebra relations,we only list some of them as follows:
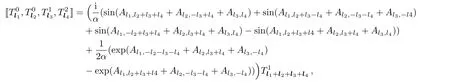

where
It is known that forneven,the super multibracket(42)with the associative operators satisfies the super GJI[29]
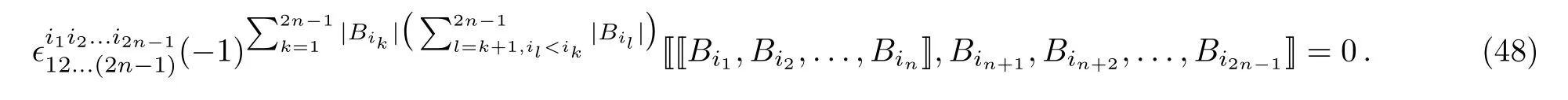
Note that the generators(40)are the associative operators.Thus(46)is a super higher order Lie algebra which satisfies the super GJI(48).
5 Summary
Recently there has been considerable interest innalgebras,especially 3-algebras,as expressed in the physics literature. In this paper we gave the operators which are indexed by thed-dimensional integer lattice. The resultingn-algebra is thed-dimensional lattice(co)sinen-algebra.Due to the associative operators,this generalized(co)sinen-algebra is the higher order Lie algebra for theneven case.We analyzed thed-dimensional lattice sine 3-algebra and found that by choosing the special parameter valueαin the 3-algebra,the correspondingd-dimensional lattice sine 3-algebra may be a Nambu 3-algebras which satisfy the so-called FI.By applying the appropriate scaling limits on the generators,we proved that thed-dimensional lattice sine 3-algebra also reduces to a nontrivial Nambu 3-algebra.Furthermore we found that thed-dimensional lattice cosine 5-algebra with the special parameter valueαmay be a higher order Lie algebra.An interesting open question is whether there exists the special parameter values such that thed-dimensional lattice sinen-algebra with oddn>5 is the Nambunalgebra or higher order Lie algebra.We also constructed the super sinen-algebra which is the super higher order Lie algebra for theneven case.It is well-known that the(super)sine algebra has the important applications in physics.As then-ary generalization of the ordinary Lie algebra structure,the applications of the(super)sinen-algebra derived in this paper should be of interest.
References
[1]C.N.Pope,L.J.Romans,and X.Shen,Phys.Lett.B236(1990)173.
[2]E.Floratos and J.Iliopoulos,Phys.Lett.B201(1988)237.
[3]I.Antoniadis,P.Ditsas,E.Floratos,and J.Iliopoulos,Nucl.Phys.B300(1988)549.
[4]E.Ramos,C.H.Sah,and R.E.Shrock,J.Math.Phys.31(1990)1805.
[5]D.B.Fairlie and C.K.Zachos,Phys.Lett.B224(1989)101.
[6]D.B.Fairlie,P.Fletcher,and C.K.Zachos,Phys.Lett.B218(1989)203.
[7]T.Dereli and A.Vermin,Phys.Lett.B288(1992)109.
[8]H.Azuma,Prog.Theor.Phys.92(1994)293.
[9]J.Bagger and N.Lambert,Phys.Rev.D75(2007)045020.
[10]J.Bagger and N.Lambert,Phys.Rev.D77(2008)065008.
[11]A.Gustavsson,Nucl.Phys.B811(2009)66.
[12]M.R.Chen,S.K.Wang,K.Wu,and W.Z.Zhao,J.High Energy Phys.12(2012)030.
[13]M.R.Chen,S.K.Wang,X.L.Wang,K.Wu,and W.Z.Zhao,Nucl.Phys.B891(2015)655.
[14]Y.X.Yang,S.K.Yao,C.H.Zhang,and W.Z.Zhao,Chin.Phys.Lett.32(2015)040202.
[15]B.Estienne,N.Regnault,and B.A.Bernevig,Phys.Rev.B86(2012)241104(R).
[16]T.Neupert,L.Santos,S.Ryu,C.Chamon,and C.Mudry,Phys.Rev.B86(2012)035125.
[17]K.Hasebe,Nucl.Phys.B886(2014)681.
[18]K.Hasebe,Nucl.Phys.B886(2014)952.
[19]C.H.Zhang,L.Ding,Z.W.Yan,K.Wu,and W.Z.Zhao,arXiv:hep-th/1606.07570.
[20]T.L.Curtright,D.B.Fairlie,and C.K.Zachos,Phys.Lett.B666(2008)386.
[21]T.Curtright,D.Fairlie,X.Jin,L.Mezincescu,and C.Zachos,Phys.Lett.B675(2009)387.
[22]S.Chakrabortty,A.Kumar,and S.Jain,J.High Energy Phys.09(2008)091.
[23]M.R.Chen,K.Wu,and W.Z.Zhao,J.High Energy Phys.09(2011)090.
[24]M.Axenides and E.Floratos,J.High Energy Phys.02(2009)039.
[25]L.Ding,X.Y.Jia,K.Wu,Z.W.Yan,and W.Z.Zhao,Nucl.Phys.B904(2016)18.
[26]Y.Nambu,Phys.Rev.D7(1973)2405.
[27]J.A.de Azc´arraga and J.M.Izquierdo,J.Phys.A:Math.Theor.43(2010)293001.
[28]T.Curtright and C.Zachos,Phys.Rev.D68(2003)085001.
[29]P.Hanlon and M.Wachs,Adv.Math.113(1995)206.
 Communications in Theoretical Physics2016年10期
Communications in Theoretical Physics2016年10期
- Communications in Theoretical Physics的其它文章
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- A Complex Network Model for Analyzing Railway Accidents Based on the Maximal Information Coefficient∗
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
