First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
Rong Yang(杨荣)Bin Tang(唐斌)Tao Gao(高涛)† and Bing-Yun Ao(敖冰云)‡
1Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China
2College of Materials Science and Engineering,Chongqing Jiaotong University,Chongqing 400074,China
3Institute of Finance&Trade,Chongqing City Management College,Chongqing 401331,China
4Science and Technology on Surface Physics and Chemistry Laboratory,P.O.Box 718-35,Mianyang 621907,China
1 Introduction
Plutonium monocarbide(PuC)is considered as one of the very promising advanced fuel materials for fast breeder reactor.Whereas plutonium dicarbide(PuC2)is often recommended to improve the performance of tristructural-isotropic(fuel)-coated particles for the veryhigh-temperature reactors.Compared with oxide fuels,carbide fuels have many advantages[1]such as good thermal conductivity,high heavy atom density and high melting point.As a consequence,modeling of the structural and physical properties of plutonium carbides from theoretical viewpoint is indispensable to their applications in the nuclear industry.
Plutonium dicarbide has tetragonal structure(CaC2type),which is isostructural with tetragonalα–UC2.[1−2]Unlike plutonium monocarbide which has been studied extensively,the investigations on plutonium dicarbide are very scarce.Experimentally,only some data on structural parameters[3]and thermodynamic properties[4−6]can be obtained.In theory,Wenet al.[7]performed a calculation on PuC2to investigate the structural,electronic and magnetic properties using the Hyed–Scuserie–Ernzerhof(HSE)hybrid functional.However,the theoretical studies of the elastic property and the chemical bonding of PuC2are still lacking.The elastic constants describe the mechanical property of materials in the region of small deformations where the stress-strain relations are still linear.The investigation on the chemical bonding can deepen the understanding of the structure of PuC2and its nature.Hence in this paper,we systematically investigate the crystal structure,magnetism,electronic structure,chemical bonding and elastic properties of PuC2.The chemical bonding and elastic properties are calculated for first time.
Since Pu is located at a special site where the transition of 5f electrons from itinerancy to localization occurs,[8]it is a considerable challenge to investigate the physical properties of PuC2theoretically.The standard local spin-density approximation(LSDA)approach underestimate the strong on-site Coulomb repulsion of the Pu 5f electrons and consequently fail to capture the electronic localization effects.The LSDA+U method with the socalled Hubbard parametric term(U)could be one way to take into account a partial localization of the 5f electrons.Recently,plutonium hydride,oxides,and monocarbide have been studied by using density functional theory(DFT)+U calculations.[7,9−10]In this paper,we use the LSDA+U approach to describe the strongly correlated metal PuC2.As for the value of U parameter,we tune it to reproduce a certain set of experimental lattice constant and other properties.
In this paper,we first use the LSDA+U scheme to investigate the structural and magnetic properties of PuC2.We find that by choosing an appropriate Hubbard U parameter around 1.5 eV,the structural parameters and magnetism for PuC2can be in good agreement with the experimental or other theoretical results.Then the electronic properties are given. Furthermore,the valenceelectron charge density and the difference charge densities along the(100)plane,the Bader charge analysis are determined to discuss the chemical bonding.Finally,we predict the elastic constants.
This paper is organized as follows.The calculation method and details are described in Secs.2 and 3,we present and discuss the results.In Sec.4,we draw our conclusions.
2 Computational Details
All our calculations are based on first-principles density functional theory with the projector-augmentedwave(PAW)method[11−12]using the Vienna ab initio simulation package(VASP)code.[13]The electronic exchange and correlation is treated within LSDA[14]and LSDA+U[15]method for strongly correlated Effect of 5f electrons.The rotationally invariant form of the LSDA+U approximation is used with a spherically averaged double counting term introduced by Dudarevet al.[16]The Dudarev approach of the DFT+U is the most widely used approach in studies of plutonium compounds.[7,9−10]Within this approach,only the difference between the spherically averaged screened Coulomb energyUand the exchange energyJis important.That is,there is one single parameter which will be calledUeff.We set the parametersU=0 eV andJ=0 eV(Ueff=0 eV);U=3.0 eV andJ=1.5 eV(Ueff=1.5 eV);U=3.0 eV andJ=0 eV(Ueff=3 eV)for LSDA+U.Through comparing with the experimental data,we choose a suitable value of the parameterUefffor PuC2.In our calculations,the nonmagnetic(NM),ferromagnetic(FM)and antiferromagnetic(AFM)states are considered.In the antiferromagnetic(AFM)calculations,we employ a 1–k AFM con figuration assuming the magnetic moments of plutonium ions lie in the plane ferromagnetically and alter their signs in the[001]direction(see Fig.1).
For the calculations of PuC2,a 6 atom conventional cell is employed.As kinetic energy cuto ffand K-point meshes are significant for the accuracy of the first principle calculations,we make a test before calculation to guarantee an excellent convergence.K-points are set to 11×7×7 and the electron wave function is expanded in plane waves up to a cutoffenergy of 500 eV.Convergence is reached when the total energies converge with 10−6eV and ionic relaxation is performed until the force acting on each atom is below the threshold of 0.001 eV/˚A.
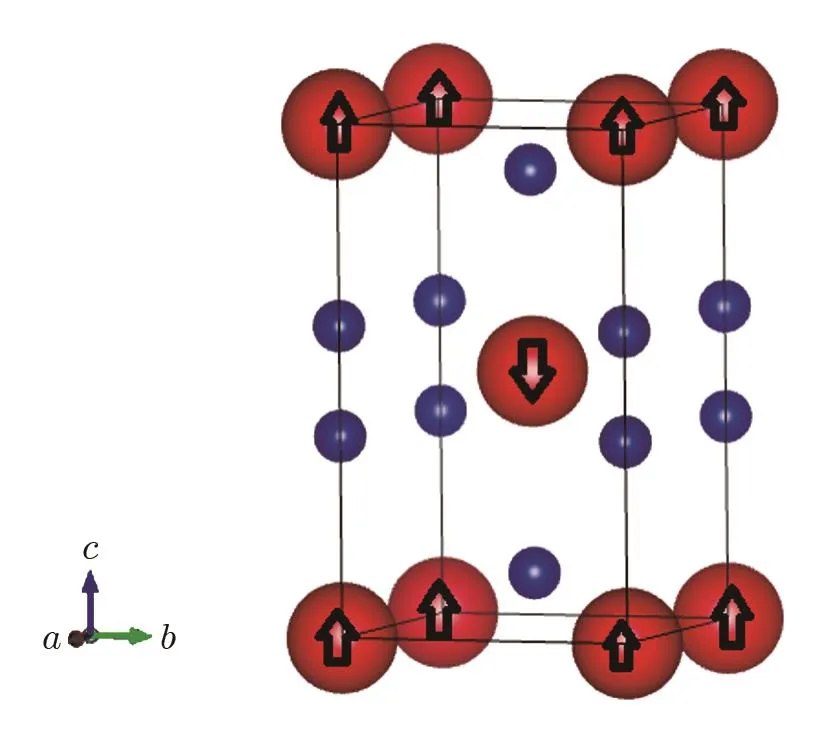
Fig.1 (Color online)The crystal structure of PuC2 with 1k antiferromagnetic(AFM)order.Red(big)balls represent Pu atoms and blue(small)balls represent C atoms.
Bader charge analysis[17]based on the quantum theory of atoms in molecules(QTAIM)is used to determine the charge transfer between Pu and C atoms.Based on the Hooke’s law,the elastic sti ff ness tensorCijklcan be expressed as:[18]
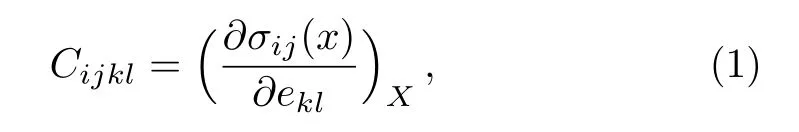
whereσijandeklrefer to the applied stress and Eulerian strain tensors,respectively,Xandxare the coordinates before and after the deformation for crystals,respectively.We calculate the elastic constants for PuC2from the “stress-strain” technique.[19]According to this method,the total energies are calculated as function of suitable applied strains.In our calculation the strain is varied in steps of 0.002 from–0.02 to 0.02.The elastic constants are obtained by fitting the energy-strain curves.For the tetragonal structure,there are six independent elastic constantsC11,C12,C13,C33,C55,andC66.
3 Results and Discussion
3.1 Structural and Magnetic Properties
The structure of PuC2is equivalent to that of CaC2,whose space group is I4 mmm(No.139).The occupied Wycko ffpositions are 2a of Pu and 4e of C.Figure 1 shows the structure of PuC2.In our calculations,the unit cell lattice parameters and atomic coordinates are fully relaxed to find the equilibrium structure.The calculated lattice constants,relative energy,magnetic moment and band gap for the nonmagnetic(NM),ferromagnetic(FM)and antiferromagnetic(AFM)states of PuC2are presented in Table 1.Table 1 shows that LSDA severely underestimates the lattice parameters,compared with the experimental data.After turning on Hubbard parameterU,an increase ofUeffleads to an increase of the lattice parameter.This can be explained as follows.With the introduction of HubbardU,the localization of the 5f electrons of Pu will be enhanced,while the cohesion of the crystal is further decreased,which leads to the increase of the lattice constant.WhenUeffis increased to 3 eV,the calculated lattice parameters are bigger than the experimental values.SoUeffwhich is bigger than 3 eV is not suitable for PuC2.
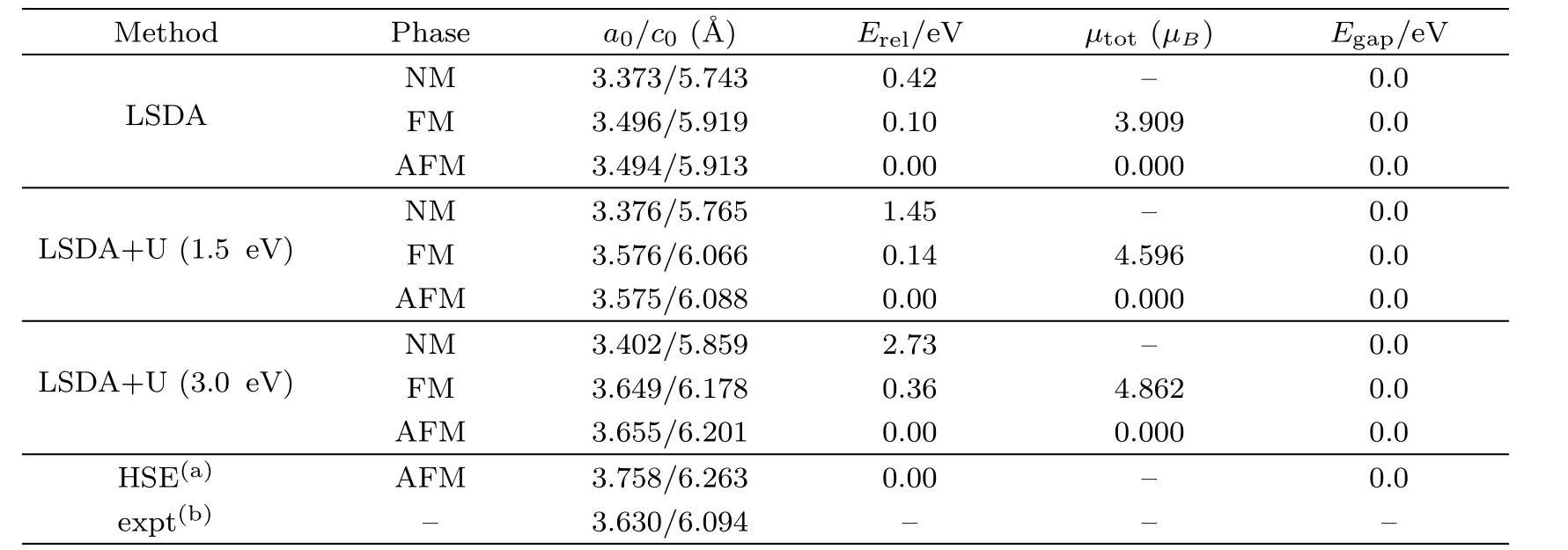
Table 1 Complication of data on NM,FM and AFM states of PuC2:lattice constant(˚A),relative energy Erel(eV/per Pu2C3or PuC2),total magnetic momentµtotand band gap(eV).
For PuC2,the total energy of the AFM phase is the lowest in LSDA,LSDA+U(1.5 eV)and LSDA+U(3.0 eV)framework.It indicates that PuC2is AFM,which is consistent with the result obtained by Wenet al.[7]For the lattice parametera0of PuC2,the discrepancy between the experiment[3]and our calculations is 3.75%for LSDA,1.52%for LSDA+U(1.5 eV)and 0.69%for LSDA+U(3.0 eV)in the AFM states.The difference of lattice parameterc0is 2.97%for LSDA,0.10%for LSDA+U(1.5 eV)and 1.38%for LSDA+U(3.0 eV)in the AFM states.Regarding the lattice parametersa0andc0,1.5 eV is suitable for PuC2.The results obtained by Wenet al.[7]are also listed in Table 1.We find that our results are better than theirs.
In brief,our results indicate that the calculated structural parameters and atomic coordinates are consistent with the experimental values.These results are sufficient to study the electronic structure,chemical bonding and elastic properties.Regarding the lattice parameters,the LSDA+U(Ueff=1.5 eV)scheme seems to be most close to the experimental value.In the following sections,our calculations are performed based on the results that PuC2is AFM.
3.2 Electronic Properties
The total and partial densities of states for PuC2in LSDA+U(Ueff=1.5 eV)are depicted in Fig.2.The total DOS curves all cross over the Fermi level(EF)with a nonzero occupation of Pu 5f electrons on it.It indicates that PuC2is metal.The lower part of the valence bands,from –7.5 eV to –15 eV,is mainly of the C 2s character.The low-lying bands,from –2.5 eV to –5 eV,are derived mainly from the C 2p states.The DOS of Pu atoms is mainly dominated by the 5f partial DOS and the Pu d orbits contribute a little to the total DOS.
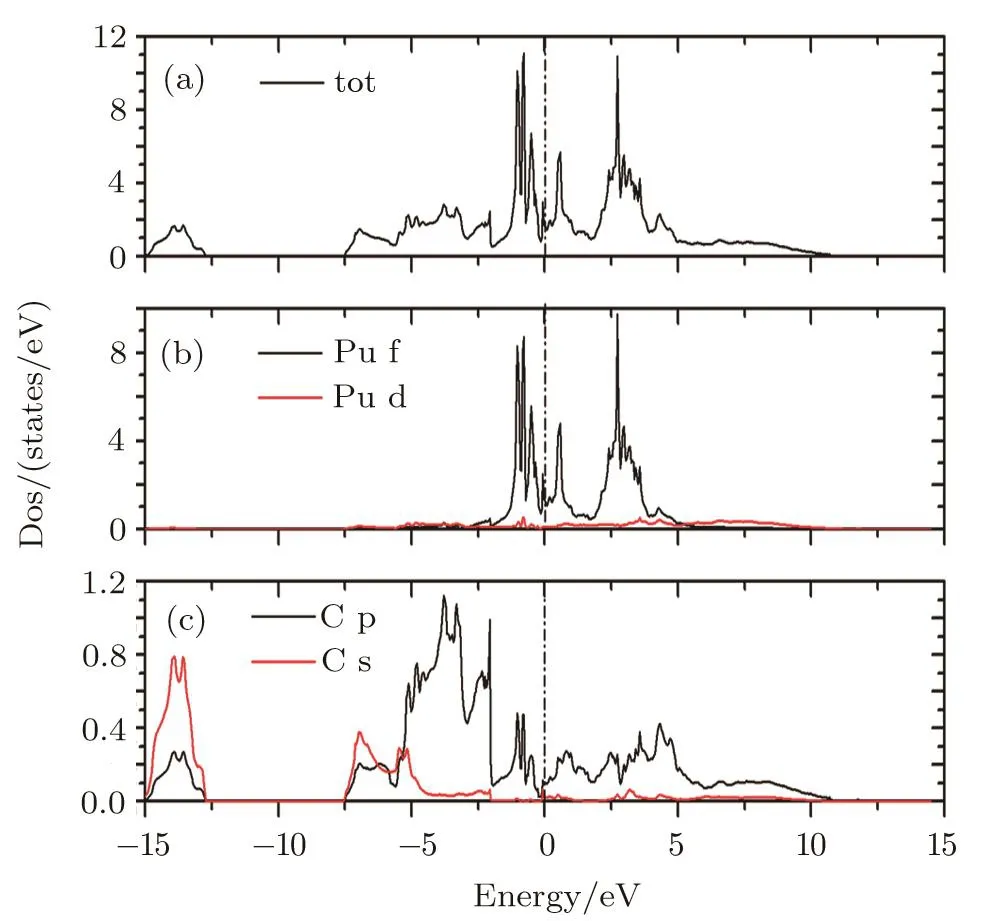
Fig.2(Color online)Total and partial densities of states for PuC2in LSDA+U(Ue ff=1.5 eV)framework.
Since we could not find any experimental data of DOS of PuC2,we will interpret it on the basis of photoelectron spectrum of Pu-based metallic systems.Photoelectron spectroscopy studies of Pu metals[20]exhibit the same type of features that the 5f states appear in the vicinity of the Fermi level and three sharp peaks appear within 1 eV,located at the Fermi energyEF,and at 0.50 eV and 0.85 eV.Obviously,the experimental studies show that the Pu 5f density of states play an important role in it.Thus the Pu 5f density of states are calculated for different values ofUeff(Fig.3).From Fig.3,no peak is found in the vicinity of the Fermi level when the value 3 eV of the Hubbard potential is used.The absence of these peaks has direct relevance to the 5f character of the calculated PuC2ground state obtained in LSDA+U(3.0 eV).When the value ofUeffis lifted,the 5f states in the vicinity of the Fermi level are reduced,which indicates that the localization of 5f electrons is highly strengthened.And we also find that the DOS of PuC2from LSDA and LSDA+U(1.5 eV)schemes have three sharp peaks within 1 eV,as is shown in Table 2.So on the basis of the lattice parameter and density of states,the LSDA+U(Ueff=1.5 eV)scheme seems to be more suitable for PuC2.
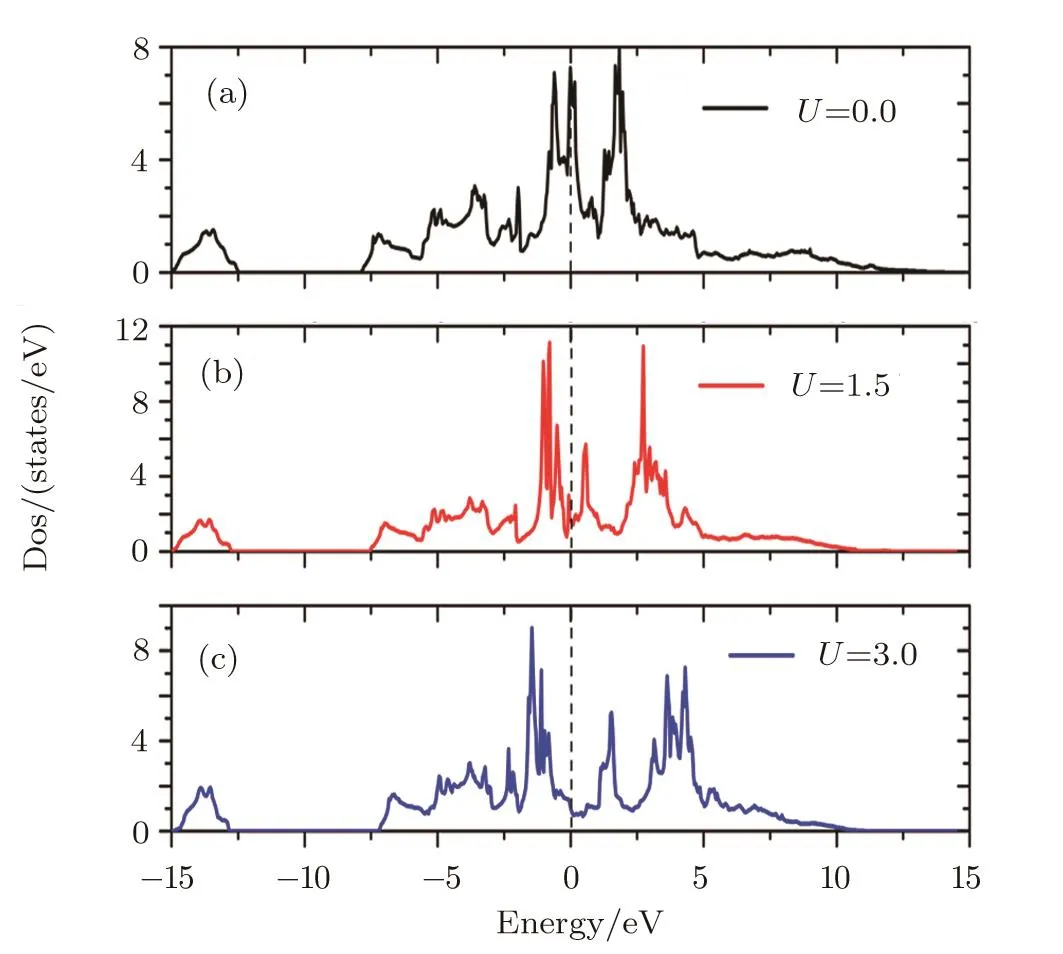
Fig.3 (Color online)Pu 5f densities of states for PuC2 calculated by LSDA+U method for different values of the U term.

Table 2 Three peaks of DOS within 1 eV located at P1,P2,and P3(in eV)for PuC2in LSDA and LSDA+U(Ue ff=1.5 eV)framework.
From the PDOS for Pu d and C s,Pu d and C p(Fig.4),we can analyze the Pu-C interaction of PuC2.The DOS of Pu d,C s,and C p have sharp peaks at the equivalent energy,which indicate that hybridization exists between Pu d and C p orbitals,Pu d and C s orbitals.The hybridization Effect implies certain covalent character in the bonding of PuC2.This can be con firmed by the later charge density analysis.
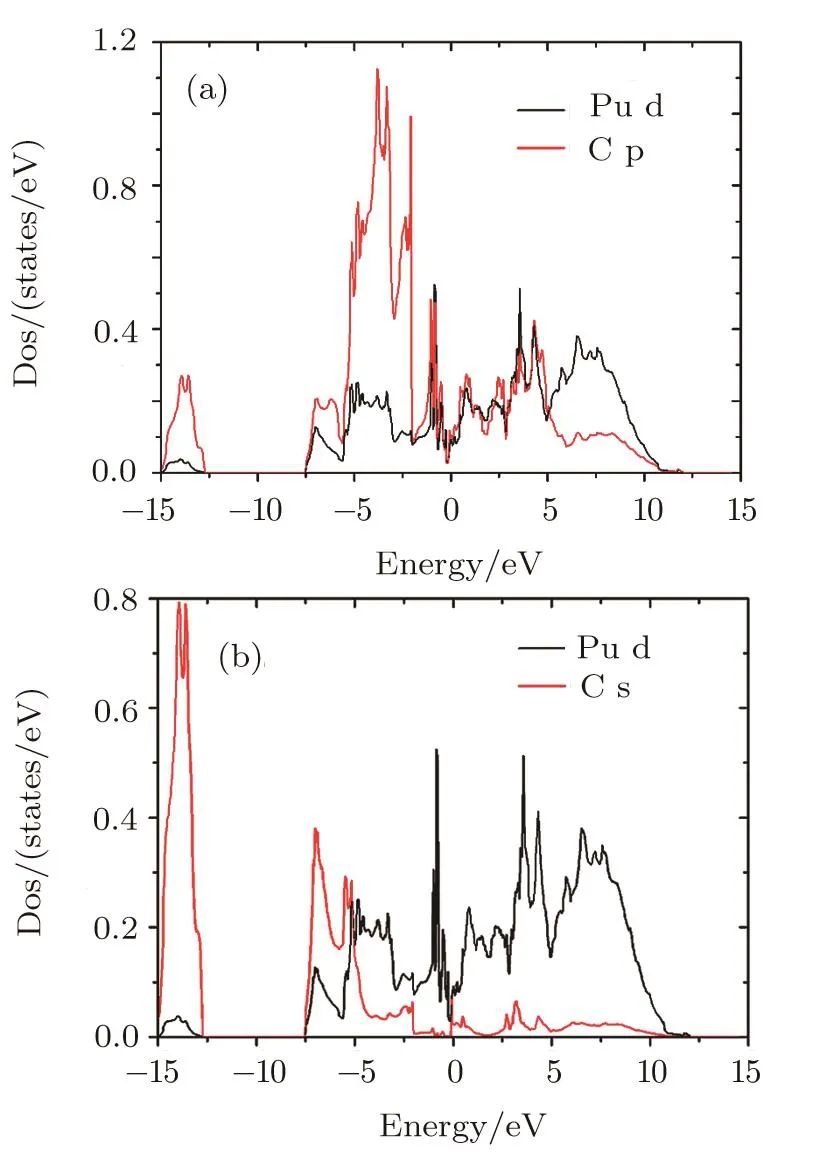
Fig.4 (Color online)partial densities of states for the(a)Pu d and C p(b)Pu d and C s of PuC2in LSDA+U(Ue ff=1.5 eV)calculations.
3.3 Chemical Bonding
In order to understand the electronic bonding character for PuC2,the valence-electron charge density and the difference charge densities along the(100)plane are plotted in Fig.5.From Fig.5(a),we can see that most of the electrons are bound around Pu atomic nuclei,only a few valence electrons can escape the bondage of the nuclei.For PuC2,the charge density distribution is largely deformed toward their bonds between the nearest C1-C2 atoms,which implies significant covalent character in the bonding of C1 and C2 atoms.This can be attributed to the sp2hybridization between C1 and C2 atoms.In the difference electron-charge density contour maps(Fig.5(b)),the blue zone and orange zone represent the loss of charge and the gain of charge.For PuC2,there is much light charge buildup with the typical characteristic of metallic bonding in the interstices regions away from the bonds,which suggests that PuC2is metallic as indicated by the DOS analysis.This can be related to part of the Pu 5f electrons transferred into the interstitial region.And we can also see that much of charge piles up in the bonding regions of Pu and C atoms.This indicates that the bonding of Pu and C atoms has certain covalent character in PuC2,as suggested by the PDOS for Pu d,C s and C p(Fig.4).Meanwhile,it is also obvious that there is net charge transferred from the Pu atom to the C atom.The feature re flects that ionic character exists in the PuC2systems.The competition between the ionic character and covalent character in the PuC2systems can be associated with the charge transferred between Pu and C atoms.We employ the bader charge analysis[17]to examine the charge transferred between the Pu atom and C atom.
We all know that Pu atom has 16 electrons outside the core,and C atom has 4 electrons outside the core.From Table 3,each Pu atom losses 1.66|e|,while a charge of 0.93|e|is transferred to C1 atom and 0.73|e|is transferred to C2 atom in PuC2system.These estimates suggest that the ionic character is weaker than the covalent character in the PuC2systems.Meanwhile,the results indicate that C1 atoms of PuC2are easier to gain electrons than the C2 atoms,namely that the ionic character of Pu-C1 is slightly stronger than Pu-C2.

Table 3 Calculated bader charges(QB)and bader volumes(VB)for AFM PuC2 in LSDA+U(Ue ff=1.5 eV)framework.
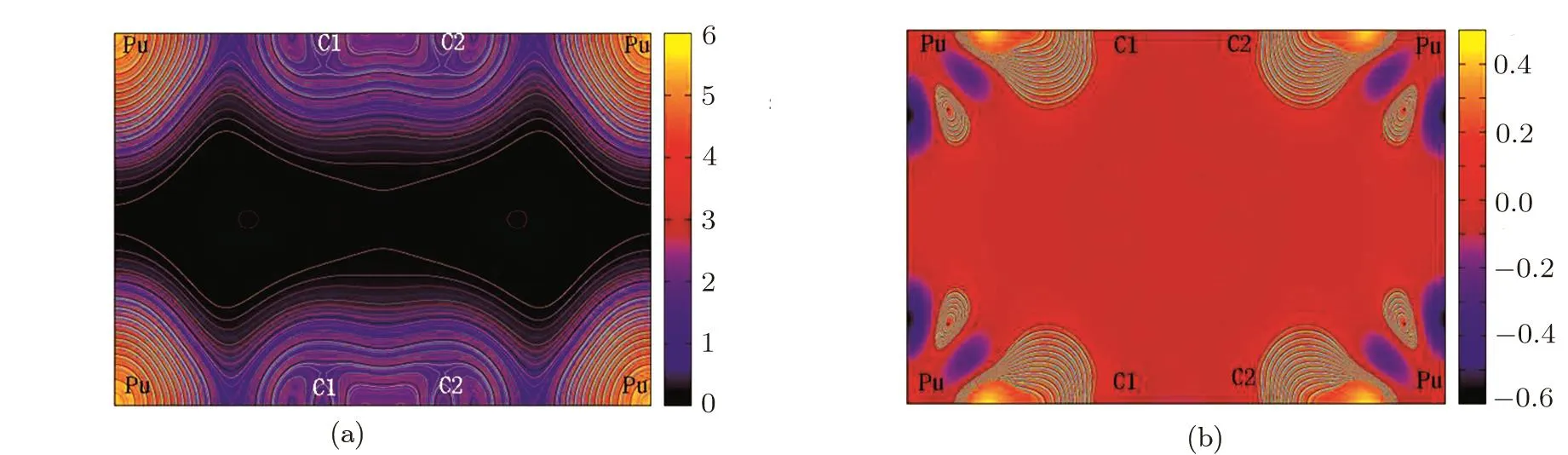
Fig.5 (Color online)Contour plots of(a)the charge density and(b)the charge density difference for PuC2 along the(100)plane in LSDA+U(Ue ff=1.5 eV)calculations.
Combining with the PDOS,the difference charge densities and the bader charge analysis,we can reach the following conclusion:(i)typical characteristic of metallic bonding are present in PuC2system;(ii)mixtures of covalent and ionic character are present in both Pu-C1 and Pu-C2 bonding,but the ionic character is slightly weaker than the covalent character;(iii)significant covalent character is present in the C1-C2 bonding.
3.4 Elastic Properties
Because the structure of PuC2belongs to the tetragonal structure,there are six independent elastic constantsC11,C12,C13,C33,C55,andC66.From the obtained elastic constants,the elastic modulus can be further calculated by Voigt[21]and Reuss[22]approximation.The Voigt bulk modulus(BV),the Reuss bulk modulus(BR),the Voigt shear modulus(GV),and the Reuss shear modulus(GR)are defined by:
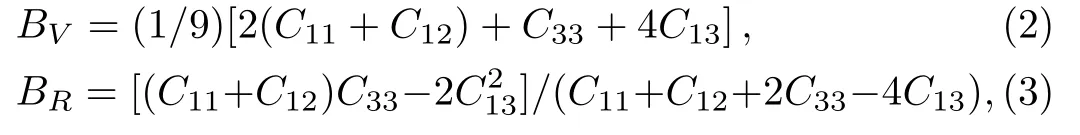
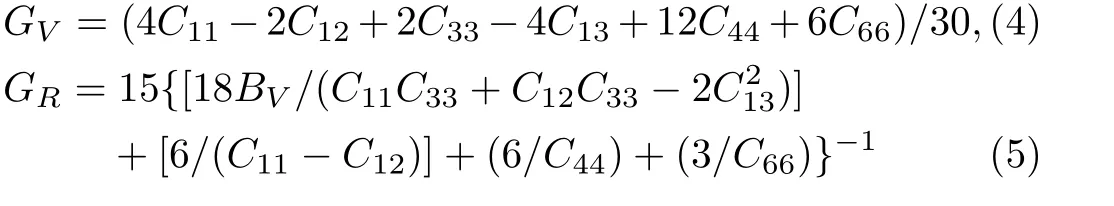
Our results are listed in Table 4.
The necessary conditions for mechanical stability are given byC11>0,C33>0,C44>0,C66>0,(C11–C12)>0,(C11+C33–2C13)>0,and[2(C11+C12)+C33+4C13]>0 for tetragonal crystal.[23]Our calculated elastic constants imply that PuC2is elastically stable.Based on Hill approximation,[24]the bulk modulusB=(BR+BV)/2 and the shear modulusG=(GR+GV)/2 can be derived.The calculatedBandGare 93 GPa and 56 GPa,respectively.G/Bcriterion can be used to predict the ductile and brittle behavior.According to Pugh’s empirical rule,[25]a higher value than the criticalG/Bratio of 0.57 associates with brittleness and a lower value corresponds to ductility.The obtainedG/Bvalue of 0.60 indicates that PuC2is a brittle material.The Poisson’s ratioσis also obtained:σ=(3B−2G)/[2(2B+G)]using the calculated bulk modulusBand shear modulusG.The calculated Poisson’s ratioσis 0.34,which is within the range(from 0.25 to 0.45)for typical metals.To the best of our knowledge,the mechanical properties have not yet been measured experimentally and calculated theoretically for PuC2,so there are currently no experimental or theoretical data for comparison.Hence we hope our results can help to provide useful reference on investigating the elastic properties of PuC2.

Table 4 Calculated elastic properties of PuC2.GV,GRare shear modulus in GPa,BV,BRare bulk modulus in GPa.
4 Conclusions
The LSDA and LSDA+U methods have been applied to systematically study the crystal structure,magnetism,electronic structure,chemical bonding,and elastic properties of PuC2.Regarding the lattice parameter and density of states,Hubbard parametric term(U)is tuned to 1.5 eV for PuC2.The optimized lattice parameters are consistent with known experimental data.The total energy calculations indicate that the ground state of PuC2is found to be AFM.This agrees with the other theoretical results.The calculated electronic properties indicate that PuC2is metallic mainly contributed by Pu 5f electrons.Through PDOS,charge density differences and bader charge analysis,the Pu-C bonding has a mixture of covalent and ionic components and the ionic character is weaker than the covalent character in the PuC2systems.Meanwhile,C1-C2 bonding has strong covalent character because of sp2hybridization between C atoms.The calculated elastic properties show that PuC2is a brittle material.We hope that our research are helpful for further studies on PuC2.
Acknowledgments
The authors are grateful to the Center of High Performance Computing Physics discipline of Sichuan University for computing.
References
[1]D.Srivastava,S.P.Garg,and G.L.Goswami,J.Nucl.Mater.161(1989)44.
[2]J.G.Reavis,M.W.Shupe,C.W.Bjorklund,and J.A.Leary,Trans.Am.Nucl.Soc.10(1967)111.
[3]D.M.Chackraburtty and N.C.Jayadevan,Acta Crystallogr.18(1965)811.
[4]C.E.Holley and Jr,The Thermodynamic Properties of Uranium and Plutonium Carbides,Los Alamos Scientific Laboratory,Los Alamos,N.M.,LADC-5487(1962).
[5]R.N.R.Mulford,F.H.Ellinger,G.S.Hendrix,and E.D.Albrecht,Plutonium 1960,Cleaver-Hume Press Ltd.,London(1961)p.301.
[6]R.N.R Mulford,J.O.Ford,and J.G.Ho ff man,Proceedings of the Symposium on Nuclear Materials,IAEA,Vienna(1962)p.517.
[7]X.D.Wen,R.L.Martin,G.E.Scueria,S.P.Rudin,and E.R.Batista,J.Phys.Chem.C117(2013)13122.
[8]S.S.Hecker,Metall.Mater.Trans.A39A(2008)1585.
[9]B.Sun,P.Zhang,and X.G.Zhao,J.Chem.Phys.128(2008)084705.
[10]J.J.Ai,T.Liu,T.Gao,and B.Y.Ao,Comput.Mater.Sci.51(2012)127.
[11]P.E.Bloechl,Phys.Rev.B50(1994)17953.
[12]G.Kresse and D.Joubert,Phys.Rev.B59(1999)1758.
[13]G.Kresse and J.Hafner,Phys.Rev.B47(1993)558.
[14]S.H.Vosko,L.Wilk,and M.Nusair,Can.J.Phys.58(1980)1200.
[15]A.I.Liechtenstein,V.I.Anisimov,and J.Zaanen,Phys.Rev.B52(1995)5467.
[16]S.L.Dudarev,G.A.Dudarev,S.Y.Savrasov,C.J.Humphreys,and A.P.Sutton,Phys.Rev.B57(1998)1505.
[17]R.F.W.Bader,Atoms in Molecules:a Uantum Theory,Oxford University Press,New York(1990).
[18]J.F.Nye,Physical Properties of Crystals,Clarendon Press,Oxford(1985).
[19]J.W.Yang,T.Gao,and L.Y.Guo,Physica B429(2013)119.
[20]T.Gouder,L.Havela,A.B.Shick,F.Huber,F.Wastin,and J.Rebizant,J.Phys.Condens.Matter.19(2007)476201.
[21]W.Voigt,Lehrburch der Kristallphysik,Teubner,Leipzig(1928).
[22]A.Reuss and Z.Angew,Math.Mech.9(1929)49.
[23]Z.Wu,E.Zhao,H.Xiang,X.Hao,X.Liu,and J.Meng,Phys.Rev.B76(2007)054115.
[24]R.Hill,Phys.Soc.Lond.65(1952)350.
[25]S.F.Pugh,Philos.Mag.45(1954)823.
 Communications in Theoretical Physics2016年10期
Communications in Theoretical Physics2016年10期
- Communications in Theoretical Physics的其它文章
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- A Complex Network Model for Analyzing Railway Accidents Based on the Maximal Information Coefficient∗
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
- In fluence of Defects and Crystallographic Orientation on Mechanical Behavior of Nanocrystalline Aluminium∗
