ZnO/ZnSe Ⅱ型同轴纳米线光学性质的模拟研究

郑晅丽，吴志明，曹艺严，孔丽晶

(厦门大学 物理科学与技术学院，福建 厦门 361005)

ZnO/ZnSe Ⅱ型同轴纳米线光学性质的模拟研究

郑晅丽，吴志明，曹艺严，孔丽晶

(厦门大学 物理科学与技术学院，福建 厦门 361005)

利用有限时域差分方法研究了纳米线直径、阵列周期和AZO衬底对ZnO/ZnSe同轴纳米线阵列光学性质的影响，并通过二维光学模式分析阐明了光吸收的物理机制. 模拟结果表明：衬底对吸收增强的程度有限且较弱；适中的填充因子将更有利于ZnO/ZnSe纳米线阵列的光吸收；较大直径的纳米线阵列可以支持更多模式的光传播，吸收率可显著增强. 而决定此异质结阵列在带隙以上吸收率的物理机制为短波长波段的周期性阵列的衍射效应及长波长波段与传导模相关的单根纳米线尺寸效应.

Ⅱ型异质结同轴纳米线阵列；ZnO/ZnSe；光学性质；有限时域差分

近年来，随着人们对半导体纳米材料的研究不断深入，新颖的材料结构不断涌现. 其中，Ⅱ型异质结同轴纳米线因其具有许多单一材料所不具备的特殊性质(例如：无需特殊掺杂就可产生类似于PN结的载流子分离效应，通过异质界面跃迁以及同轴纳米线的陷光效应提高光吸收和光电转化效率，等等)，有望成为未来光伏器件的重要组成部分[1-2]. 相比于其他金属氧化物材料，ZnO来源丰富，生长技术相对成熟，化学性能稳定，安全无毒，以其作为核或壳的Ⅱ型异质纳米结构材料的研究已引起研究人员的极大兴趣. 研究表明纳米线阵列的结构参量等对其吸收性质影响巨大[3-4]，且阵列的光学属性又是决定其光伏器件效率的关键因素. 因此，探讨各结构参量对ZnO/ZnSe Ⅱ型同轴纳米线阵列光学性质的具体影响，分析其中潜在的物理机制，对于此类太阳能电池的制作很有意义. 本文利用有限时域差分方法(Finite difference time domain,FDTD)分析了纳米线直径、阵列周期和AZO衬底对ZnO/ZnSe同轴纳米线阵列的光学性质的影响，阐明了决定其2.70 eV以上吸收率高低的2个主要物理机制. 目前，该仿真实验作为研究性实验项目引入物理开放性实验教学，克服了传统实验教学方式受时间、空间限制的困扰，通过构建模型、编写程序代码和分析数据等一系列自主学习过程，让学生尽早地接触科研、体验科研、感受科研的魅力，为他们后续的发展打下坚实的基础.

1 数值计算原理

1.1 模拟的几何结构及参量设置

图1为模拟的ZnO/ZnSe同轴纳米线阵列的结构示意图. ZnO/ZnSe同轴纳米线为圆柱形结构，而且按正方形周期排布，垂直生长在AZO(ZnO∶Al-glass)透明导电薄膜上. 背景介质为空气. 入射的平面光波沿z轴方向传播，电场的极化方向平行于x轴.

图1 ZnO/ZnSe同轴纳米线阵列结构示意图

本文中所涉及参量：L为纳米线的长度，D1和D2分别代表ZnO核层的直径和ZnO/ZnSe纳米线的总直径，阵列周期P定义为两相邻纳米线中心间的距离，填充因子ff等于D2/P. 为了尽量简化计算过程，节约计算时间，并考虑实际生长和应用需要，固定纳米线长度L、掺Al的ZnO层厚度、玻璃基底厚度均为1 μm，D1为50 nm. 分别从60～270 nm改变D2的大小，步距为30 nm，从0.2～1改变ff，步距为0.1，计算不同几何配置下阵列的吸收谱、反射谱、透射谱和单位体积吸收率的空间分布.

1.2 阵列光学性质分析方法

根据坡印廷矢量的定义有

S=E×H,

(1)

通过FDTD算法求解麦克斯韦旋度方程可以得到不同波长下电磁场的空间分布，由此求出坡印廷矢量的大小. 同轴纳米线内单位体积的吸收率可表示为

A(r,λ)=0.5Re [·S].

(2)

由式(1)和式(2)可得

(3)

则不同波长下纳米线阵列的总吸收率为

(4)

式中:c为真空光速，λ为光波波长，r为位置矢量，E为电场强度，ε为材料的电容率. 文中所用的ZnO(ZnO∶Al)、ZnSe等材料的折射率和消光系数分别来自参考文献[5-6].

1.3 二维光学模式分析方法

模式m在纳米线顶部的电磁场能量为

Pm(z=0)=PincTmηm,nor,

(5)

式中：Tm为模式m在纳米线顶部(z=0)处透射率，Pinc为入射光的能量，ηm,nor为归一化后模式m与入射光的耦合效率，代表了入射光与模式场的相关度. 根据比尔-朗伯定律，沿纳米线轴向传播的模式m的电磁场能量符合指数衰减规律，即

Pm(z+L)=Pm(z)e-αmL,

(6)

由式(5)和式(6)可推导出模式m在纳米线内的吸收率为

Tmηm,nor(1-e-αmL).

(7)

这里假设每个模式都彼此独立、互不干扰，并且定义吸收率大于1%的光学模式为主模式.

2 结果与讨论

2.1 不同几何参量对ZnO/ZnSe纳米线阵列光学性质的影响

图2所示为D2=120 nm、ff=0.5与D2=180 nm、ff=0.3时，有AZO衬底和无AZO衬底情况下ZnO/ZnSe纳米线阵列的吸收谱. 通过比较同一几何配置下的2条吸收谱，可以发现AZO衬底的存在导致吸收谱出现间距较宽的小幅振荡，使纳米线阵列的吸收率得到一定程度的增强，在λ=300～500 nm波段内，上述2种配置结构的吸收率分别增强了0.42%及8.1%. 值得注意的是，这些小幅振荡主要是由纳米线顶部与底部之间弱的法布里-珀罗共振引起，这与Si等间接带隙半导体材料构成的纳米线阵列不同[9]，衬底对吸收增强的程度有限且较弱，绝大部分的入射光被ZnO/ZnSe同轴纳米线吸收.

图2 不同几何配置下，AZO衬底对ZnO/ZnSe 纳米线阵列吸收性质的影响

为了阐明阵列周期P对ZnO/ZnSe纳米线阵列光学特性的影响，固定纳米线直径D2为120 nm，计算不同阵列周期P(ff=0.3～1.0)下阵列的吸收、反射和透射谱，如图3所示.

(a)吸收谱

(b)反射谱

(c)透射谱图3 D2=120 nm时，不同阵列周期P下ZnO/ZnSe 纳米线阵列的光学性质

在短波长区域(即λ<400 nm)：当P从120 nm增大到200 nm时，阵列的透射率几乎均为0，说明此时阵列的吸收率主要由其反射率决定. 与此同时，3种几何配置下的阵列的吸收率随着P的增大而逐渐增大，这可能是因为在这一波段ZnSe具有较大的消光系数；当P在240～300 nm范围内，随着P的持续增大，阵列的反射率逐渐下降，此时阵列的吸收率主要由其透射率决定，同时吸收谱前端出现的波谷也随之展宽加深，阵列的吸收率逐渐下降，这可能是入射光在纳米线间的衍射过程减弱所引起的[10]；当P>300 nm后，随着P的增大，相邻纳米线间的相互作用减弱，使阵列的透射率和反射率均大幅度提高，最终导致其吸收率显著下降. 在长波长区域(即λ>400 nm)：反射率随P的增大呈现逐步减弱趋势，阵列的反射被很好地抑制；此时，由于纳米线层不充足的光吸收，光将到达衬底表面，导致透射率在各几何配置下均显著增强；同时，由于发生光散射增强的能量区域向长波长方向移动，可以观察到图3(a)的吸收谱发生了红移. 综上所述，适中的填充因子将更有利于ZnO/ZnSe纳米线阵列的光吸收.

近年来，研究者发现纳米线阵列本征的抗反射效应和共振模式的有效激发是其吸收率增强的主要原因[11-12]. 为了验证这一观点并且阐明纳米线直径D2对阵列光学性质的影响，固定填充因子ff为0.5，计算不同纳米线直径D2下阵列的吸收谱、反射谱和吸收率在x-z平面内的空间分布，如图4所示. 从图4(b)中可以清楚地看到：除了D2=60 nm的反射率曲线在长波长区域出现了几个起伏较大的反射振荡峰，使纳米线阵列在300～500 nm的波长范围内的总反射率超过4%，其余6种几何配置的总反射率均小于4%，证明ZnO/ZnSe纳米线阵列的确具有良好的抗反射特性. 另外，图4(a)显示：在长波长区域(即λ>360 nm)，随着D2从60 nm增大到120 nm，阵列的吸收率由于吸收边的红移而显著增大；相反地，当D2超过150 nm，吸收率开始逐渐减小. 同时，由图4(c)可知，D2为60 nm的阵列中，光吸收分布较为单一和分散；相反，在D2为120 nm的阵列中，光吸收主要沿纳米线轴向呈漩涡状分布；而当D2超过150 nm后，场分布越发不集中，这是导致图4(a)中吸收率随D2的增大最终逐渐下降的原因. 图4(c)的这些现象说明对于小直径的纳米线，只能支持少量的模式在纳米线阵列内传播，入射光只能通过较为单一的路径被纳米线阵列吸收，因此吸收率较低；相比之下，较大直径的纳米线阵列可以支持更多模式的光传播，吸收率可显著增强.

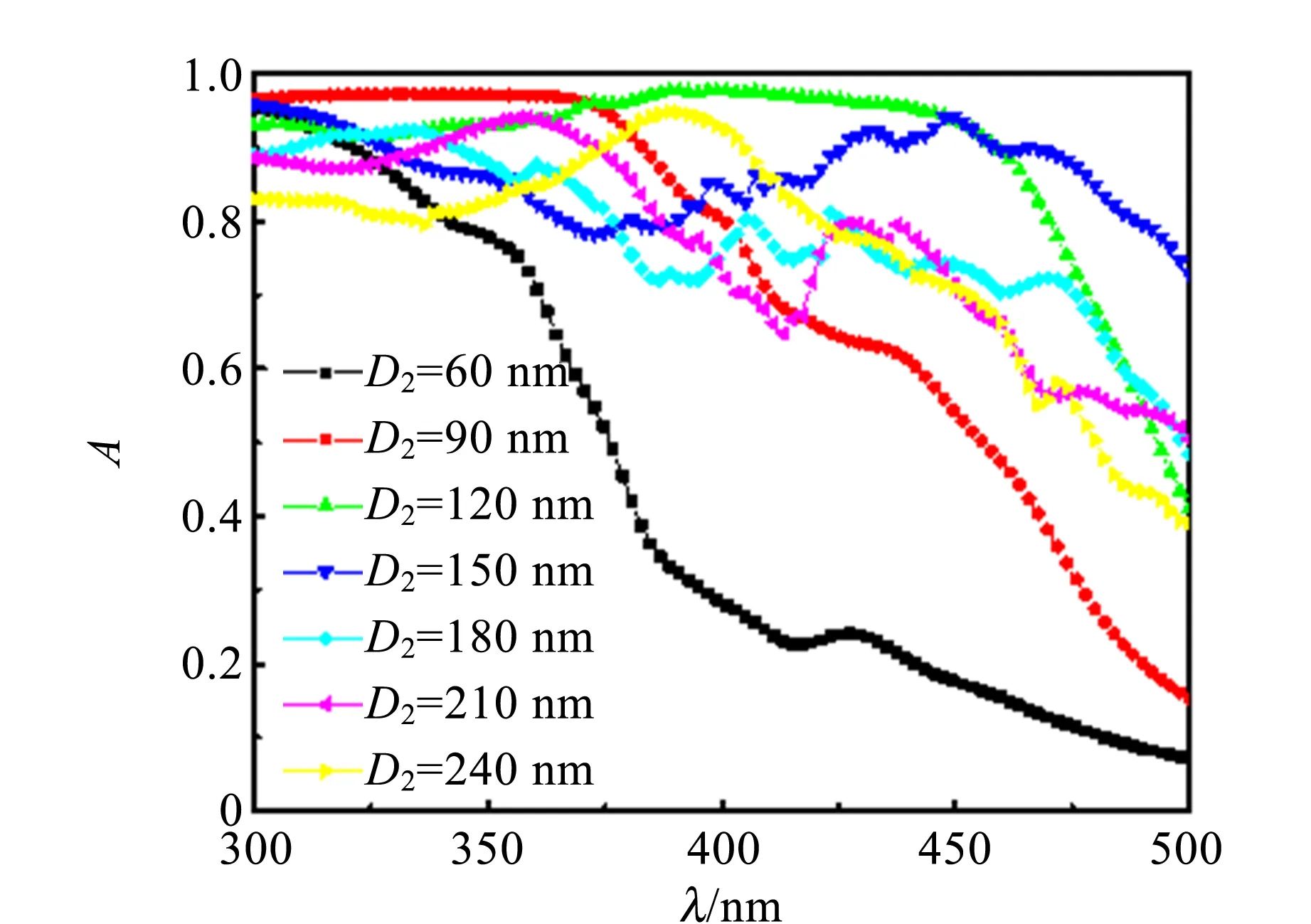
(a)吸收谱

(b)反射谱

(c)吸收率在x-z平面的空间分布图4 ff=0.5时，不同纳米线直径D2下ZnO/ZnSe纳米线阵列的光学性质

2.2 光学模式分析

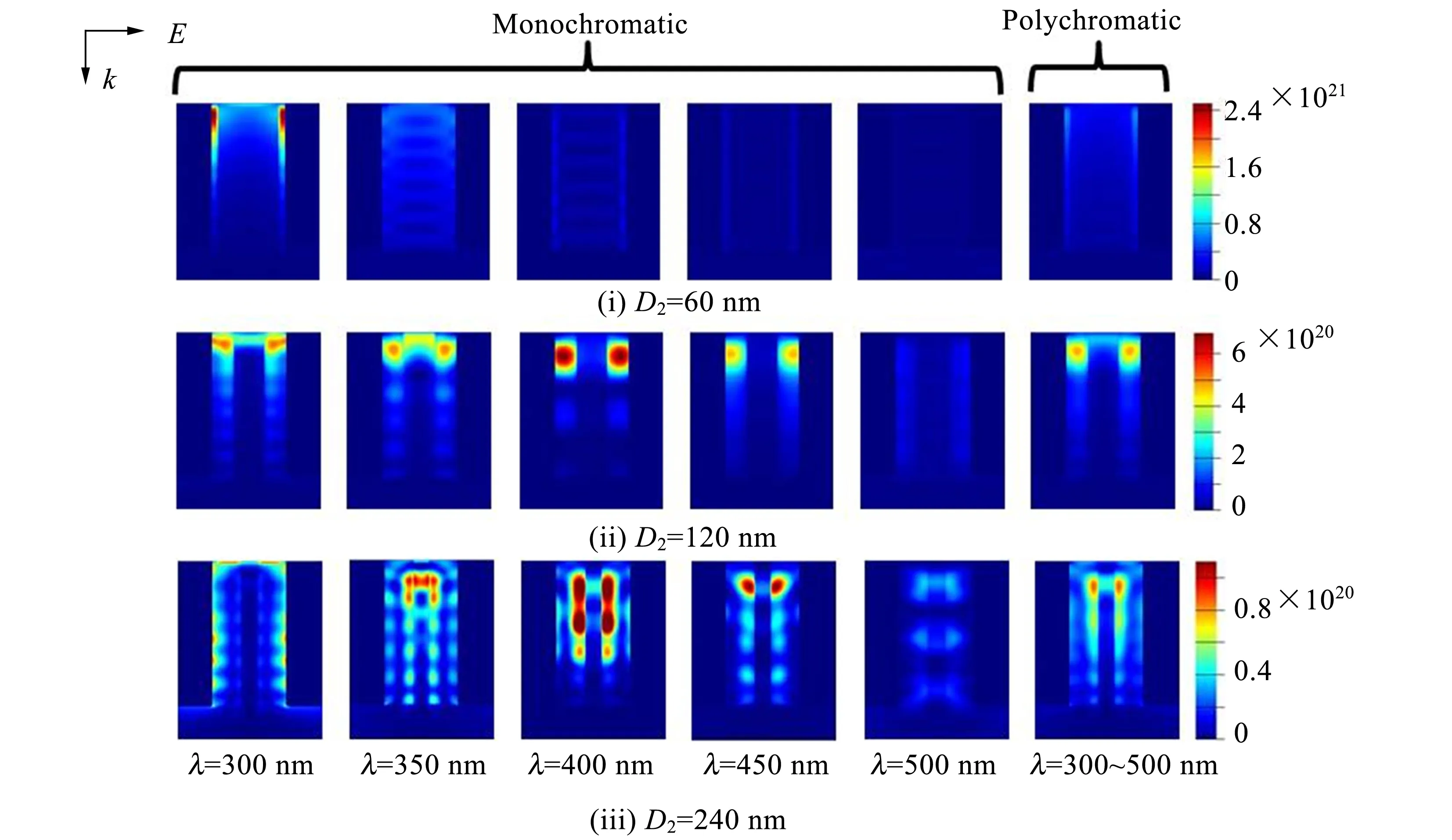
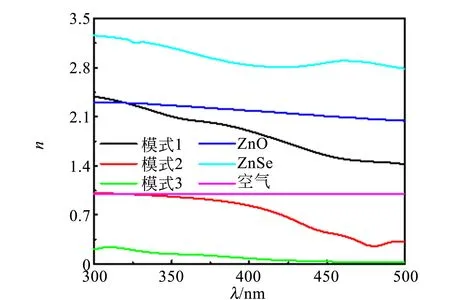
为了更进一步理解波导共振对纳米线光吸收过程的作用，计算了阵列的最优吸收率(由光吸收率对300～460 nm范围的波长积分得到)，并对最佳几何配置(D2=120 nm,P=240 nm)下的阵列进行二维光学模式分析，如图5所示. 为了排除法布里-珀罗共振对阵列吸收率的影响，这里仅考虑无衬底的ZnO/ZnSe同轴纳米线阵列的情况. 图5(b)显示，3个主模式(A>1%的光学模式)的总吸收谱线与纳米线阵列的吸收谱线基本吻合，说明纳米线阵列的光吸收主要由这3个主模式决定. 从图5(a)的光学模式的有效折射率随波长变化曲线可以看到，在300～500 nm波段内，3个主模式中只有模式1的有效折射率介于ZnSe与空气的折射率之间，满足光波导条件，属于完全的传导模. 模式2在λ<318 nm波长范围内的有效折射率略大于1，为传导模，在这之后的长波长区域内逐渐衰减为辐射模. 模式3在全波段内的有效折射率均小于1，为完全的辐射模.

从图5(b)可知模式1和2对纳米线阵列总的光吸收的贡献最大，分别为59.0%及26.3%. 在λ<355 nm的短波长区域内，模式1的有效折射率与ZnO的折射率接近，因此，其与入射光的空间耦合度差，对纳米线阵列的吸收贡献小. 另一方面，模式2的有效折射率接近空气的折射率，因此，该模式与自由空间阻抗匹配使其与入射光有效耦合. 同时，如图5(c)所示，模式2的电场紧紧地围绕在纳米线周围，说明在此阵列周期(P=240 nm)情况下相邻纳米线间光的相互作用巨大. 上述2个条件将很可能导致衍射现象的发生，最终导致模式2在这一波段的吸收率高达50%，这与之前的猜测一致；当λ>355 nm之后，模式1的吸收率均大于40%，且其吸收峰位置(λ=457 nm)与纳米线阵列的吸收峰位置一致，说明在这一波段，纳米线阵列的吸收率主要由模式1控制. 这主要是因为此波段模式1与入射光的耦合效率高，而其他模式与入射光的耦合效率逐渐降低.

(a)有效折射率随波长变化曲线

(b)吸收谱

(c)电场在x-y平面的空间分布(模式2)图5 D2=120 nm、P=240 nm下，ZnO/ZnSe同轴纳米线阵列中各模式的光学性质

3 结束语

利用FDTD算法计算了不同几何配置下ZnO/ZnSe同轴纳米线阵列的光学性质，获得不同几何参量对其光吸收特性的影响，阐明决定该异质结阵列在带隙以上吸收率高低的两大物理机制——短波长波段的周期性阵列的衍射效应及长波长波段与传导模相关的单根纳米线尺寸效应. 该理论还可应用于解释其他直接带隙半导体材料，如CdSe和CdS等作为壳层的ZnO基Ⅱ型同轴纳米线阵列的光吸收过程. 同时，此模拟项目已成功转化为开放性实验教学内容，通过科研成果与实验教学的有机结合，使学生能接触和了解与本学科相关的最新进展，激发和培养他们的创新思维和科研能力.

[1] Wu Z M, Zhang Y, Zheng J J, et al. An all-inorganic type-Ⅱ heterojunction array with nearly full solar spectral response based on ZnO/ZnSe core/shell nanowires [J]. J. Mater. Chem., 2011,21(16):6020-6026.

[2] Gu Z, Prete P, Lovergine N, et al. On optical properties of GaAs and GaAs/AlGaAs core-shell periodic nanowire arrays [J]. J. Appl. Phys., 2011,109(6):064314-064314-6.

[3] Hu L, Chen G. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications [J]. Nano Lett., 2007,7(11):3249-3252.

[4] Xie W Q, Liu W F, Oh J I, et al. Optical absorption in c-Si/a-Si:H core/shell nanowire arrays for photovoltaic applications [J]. Appl. Phys. Lett., 2011,99(3):033107-033107-3.

[5] Michallon J, Zanuccoli M, Kaminski-Cachopo A, et al. Comparison of optical properties of Si and ZnO/CdTe core/shell nanowire arrays [J]. Materials Science and Engineering B, 2013,178(9):665-669.

[6] Connolly J, diBenedetto B, Donadio R. Specifications of Raytran material [J]. Proc. SPIE, 1979, 181:141-144.

[7] 陈根祥,路慧敏,陈勇,等. 光钎通信技术基础 [M]. 北京:高等教育出版社,2010.

[8] Kupec J, Witzigmann B. Dispersion, wave propagation and efficiency analysis of nanowire solar cells [J]. Optics Express, 2009,17(12):10399-10410.

[9] Zanuccolia M, Michallon J, Semenihinc I, et al. Numerical simulation of vertical silicon nanowires based heterojunction solar cells [J]. Energy Procedia, 2013,38:216-222.

[10] Li J, Yu H, Li Y. Solar energy harnessing in hexagonally arranged Si nanowire arrays and effects of array symmetry on optical characteristics [J]. Nanotechnology, 2012,23(19):194010.

[11] Wen L, Li X, Zhao Z, et al. Theoretical consideration of Ⅲ-V nanowire/Si triple-junction solar cells [J]. Nanotechnology, 2012,23(50):505202.

[12] Fountaine K T, Whitney W S, Atwater H A. Resonant absorption in semiconductor nanowires and nanowire arrays: Relating leaky waveguide modes to Bloch photonic crystal modes [J]. J. Appl. Phys., 2014,116(15):14302.

[责任编辑：任德香]

Simulation on the optical properties of ZnO/ZnSe type-Ⅱ coaxial nanowire arrays

ZHENG Xuan-li, WU Zhi-ming, CAO Yi-yan, KONG Li-jing

(Department of Physics, Xiamen University, Xiamen 361005, China)

The effects of nanowire diameter, array period and AZO substrate on the optical properties of ZnO/ZnSe coaxial nanowire arrays were studied by finite difference time domain method. The absorption mechanisms of the heterostructure were elucidated through two-dimensional optical mode analysis. The simulation results showed that the absorption enhancement of the substrate was limited and weak, moderate fill factor would be conducive to the absorption of ZnO/ZnSe nanowire arrays. Larger nanowire diameter could support more models of light transmission and enhance the absorptivity significantly. The absorptivity mechanisms of the heterojunction arrays above the band gap depended on the diffraction effect of the periodic arrays in short wavelength band and the size effect of single nanowire associated with the transmission model in long wavelength band.

type-Ⅱ heterojunction coaxial nanowire arrays; ZnO/ZnSe; optical property; finite difference time domain

2016-05-30

郑晅丽(1983-)，女，福建厦门人，厦门大学物理科学与技术学院工程师，硕士，研究方向为太阳能电池.

O43

A

1005-4642(2017)02-0001-06

“第9届全国高等学校物理实验教学研讨会”论文