浅水中爆炸水底介质对水中冲击波峰值压力影响的试验研究

王振雄， 顾文彬， 陈江海， 徐景林， 刘 欣， 陆 鸣

(1.解放军理工大学 野战工程学院，南京 210007； 2.武汉军械士官学校，武汉 430075)

浅水中爆炸水底介质对水中冲击波峰值压力影响的试验研究

王振雄1， 顾文彬1， 陈江海1， 徐景林1， 刘 欣1， 陆 鸣2

(1.解放军理工大学 野战工程学院，南京 210007； 2.武汉军械士官学校，武汉 430075)

作为评判水中爆炸冲击波强度的一个重要因素，水中冲击波峰值压力研究至关重要。在满足爆炸相似律的基础上对水中爆炸试验的相似要求进行推导，建立试验条件下水中冲击波峰值压力的回归模型。在两种水底介质、不同水深情况下进行试验，采集不同测点的水中冲击波的峰值压力，运用π定理和量纲分析、最小二乘法对试验数据进行分析，得出了符合爆炸相似律的公式，并验证了回归公式的准确性。通过显著性检验可知浅水中爆炸中测点和装药的距离对水中冲击波峰值压力的影响最大，水深因素的影响可忽略。对不同水底介质试验中的数据分析得出水底介质对峰值压力影响较大，软泥夹石水底试验中测得冲击波峰值压力约为软泥水底试验中冲击波峰值压力的4/3倍。

水中爆炸；冲击波峰值压力；相似理论；试验研究

水中冲击波是装药在浅水中爆炸形成的造成目标破坏的重要原因，其破坏效果与目标形状、结构及材料性质等有很大的关系，峰值压力通常用来评判水下爆炸的冲击波强度。随着水中爆炸载荷测试技术的发展，给水中冲击波峰值压力的研究带来了方便[1]，国内外研究人员对水中爆炸产生冲击波进行过许多试验研究。BJARNHOLT[2]曾提出一种水中爆炸压力测试和数据评估的新方法；HAMMOND[3]对柱形装药在水中爆炸的研究表明近距离范围内, 装药形状对爆炸冲击波性能有很大影响；MICHAEL等[4]通过测试分析，认为装药半径与装药密度对水中冲击波压力有影响；李澎等[5]曾对水下爆炸冲击波传播近似计算进行过研究；李金河等[6]通过对不同种类装药在水中爆炸冲击波性能参数及其相似常数的研究说明含铝炸药水中爆炸冲击波远场的传播服从指数变化的相似律, 其冲击波性能比标准炸药TNT优越；COLE等[7]在总结前人成果的基础上，通过大量的试验研究，全面阐述了水下爆炸的物理现象和基本规律，建立了一定范围内爆炸流场中冲击波峰值压力、比冲量及能量密度的计算公式。 对于水中冲击波的研究主要集中在：冲击波峰值压力的测试；冲击波在自由面影响下的压力特性研究及边界条件影响下的传播规律以及通过水中冲击波来反推炸药的一些参数等。

浅水中爆炸冲击波要受到水面和水底两种界面的影响，在水面和水底要经过多次反射、透射,所产生的波系的相互作用使得问题更加复杂化[8]。影响冲击波峰值压力的主要因素有水深、炸高、测点位置(测点距离装药中心的水平距离及测点距离水底的距离)，装药量与装药性能参数以及水底介质参数也在很大程度上影响着冲击波的峰值压力。由于水底的影响较为复杂，对有水底影响的冲击波压力特性研究还比较少，对于同时受水底水面影响的浅水中爆炸冲击波压力特性研究则更少[9]。要考虑各种因素对冲击波影响，尚无法建立一个合理的理论计算模型。本文在相似理论的基础上建立峰值压力的回归模型，采用0.4 kg压装TNT进行试验，不同水底介质情况下，对不同因素影响下的测点的冲击波峰值压力进行采集，通过数据拟合回归出冲击波压力峰值计算公式，进行显著性检验分析对冲击波压力峰值影响较大的因素，并且得出不同水底情况下，冲击波峰值压力的计算公式。

1 试验的相似要求及相似条件的确定

为了验证水中冲击波的相似律，库尔进行了大量的试验表明所有水冲冲击波参数因药量和距离的变化都可精确的预估，也证明了水中爆炸相似律是冲击波的普遍规律。但由于药包近区的特殊性，相似律验证区域通常为水中压力180 MPa以内的范围，约相当于7倍球形装药半径外的区域[10-11]。根据爆炸相似理论，原型试验与试验之间至少要满足三个基本相似要求，即：几何相似、运动相似和动力相似。三个基本要求是必要的，但是不是充分的。在不考虑水的黏性和重力条件下，制约浅水中爆炸作用参数包括：几何参数、水介质参数、水底介质参数、炸药参数和水中冲击波参数。制约浅水中爆炸冲击波参数的各因素及量纲见表1。

表1 浅水中爆炸的主要物理量

选取E(ML2T-2)、r(L)、C(LT-1)三个物理量为基本物理量。根据爆炸相似理论，在模型与实物之间的无量纲参数应该保持不变，则要求试验的相似条件满足采用相同的试验水介质(含静水压力相等)，且水底地质条件相同；采用相同种类及密度的炸药；水深、装药到水底的距离、装药中心到测点的水平距离、测点到水底的距离与装药半径几何相似；装药形状几何相似，且装药量与装药半径的立方成正比。

若上述试验相似条件成立，即原型试验与试验物理上相似，即满足

(1)

2 峰值压力回归模型建立与回归分析方法

2.1 峰值压力拟合模型

装药与测点几何参数的相对位置示意图(见图1)。

图1 测点相对位置关系示意图Fig.1 Diagram of measuring points

由于pm≫p0，pm的大小取决于装药的总能量E、装药距离水底的距离H、测点距离水底的距离h、水深d、测点到装药的水平距离L以及p0和ρ0，写成函数表达式为

pm=φ(H,h,d,L,E,p0,ρ0)

(2)

如果选择E、p0和ρ0为独立变量，根据π定理可以得出

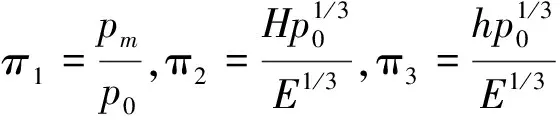
由此，冲击波峰值压力与装药及测点位置的关系可表示为

Φ(π1,π2,π3,π4,π5)=0

(3)

由于E=CQ(C为装药质量;Q为爆热)，在Q、p0一定的条件下，式(3)可以写成

(4)

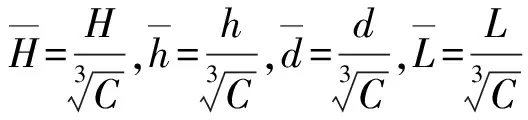
则

(5)

式中，系数A及指数a1，a2，a3，a4由试验数据确定。

2.2 试验系数回归方法

对式(5)两边取对数

(6)

即

Y=a0+a1X1+a2X2+a3X3+a4X4

(7)

根据最小二乘法，选取ai(i=0,1,…,4)使剩余平方和有极小值

(8)

式中:n为峰值压力统计表中的测点数；Yj为统计表中第j个峰值压力；X1j、X2j、X3j、X4j分别为式(7)中变量X1、X2、X3、X4对应的Yj的设置参数。要使Q有极小值，ai(i=0,1,…,4)必需满足

(9)

由式(9)可得方程组

(10)

其中

(11)

解方程组(10)的系数矩阵，可求得ai(i=0,1,…,4)。

2.3 回归精度分析

在多元线性回归中，变量之间的相关系数很复杂。任意两个变量之间都可能存在着相关系数。当自变量之间的相关性很大时，会对因素分析带来很大麻烦。Xi、Xj之间的相关系数由式(12)计算

(12)

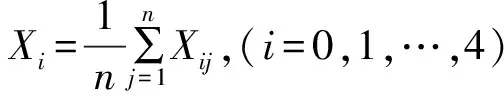
求出回归系数后，还应该计算并分析回归精度以及剩余平方和

(k=0,1,…,4)

(13)

U越大，表示回归的规律性越强，效果也就越好；剩余标准差

(14)

回归均方与剩余均方比

(15)

利用F值可以对整个回归进行显著性检验，即Y与所考虑的k个自变量X1，X2，X3，…,Xk之间的线性关系究竟是否显著。

3 试验数据及分析

通常在浅水中爆炸时，爆炸能量一部分消耗在水底介质的破碎或抛掷上；一部分转化为震动能量，以地震波的形式在水底传播；另一部分能量以水中冲击波的形式在水中传播，三者的能量分配无论在理论上或试验测量中研究都比较困难。水中产生的扰动在水域的自由面和底面之间传播，扰动在两个界面处反射，并产生相互作用而引起复杂的波系，因此浅水中爆炸应当考虑水域自由面和底面的联合影响[12]。装药在水中爆炸，产生的水中冲击波以球形向外传播，在水中直接传播至测点位置，如图1中1所示；当冲击波传至自由水面时，冲击波在水面处发生反射，反射波类似在空气中的镜像炸药爆炸产生的冲击波在水中继续传播如图1中的2所示；与自由水面的影响相同，水中爆炸的冲击波作用在水底，使水底快速变形，并被压实，产生反射波在水下传播如图1中3所示。装药与测点的相对位置不同，测点所受的压力也会不同，测点的峰值压力是图1中1，2和3的共同作用的结果，但相对位置的不同，三者的影响程度也会不同。

为了对水中冲击波峰值压力的影响因素进行研究，采用0.4 kg的立体压装TNT进行试验，爆破测试区域及传感器设置图如图2、图3所示。对不同水深、炸高、测高及水平距离的测点峰值压力进行测量，并对不同水底介质的测点进行监测，获得不同情况下的冲击波峰值压力，将测得数据导出通过Matlab处理可得冲击波压力时程曲线，测点的典型冲击波压力时程曲线如图4所示[13]。根据回归模型对数据进行处理，进而分析影响浅水中爆炸水中测点峰值压力的主要因素，拟合得出浅水中峰值压力计算公式，对公式回归精度进行分析并验证其准确性。

图2 传感器设置图Fig．2Settingsofaensor图3 试验区域Fig．3Experiments’area

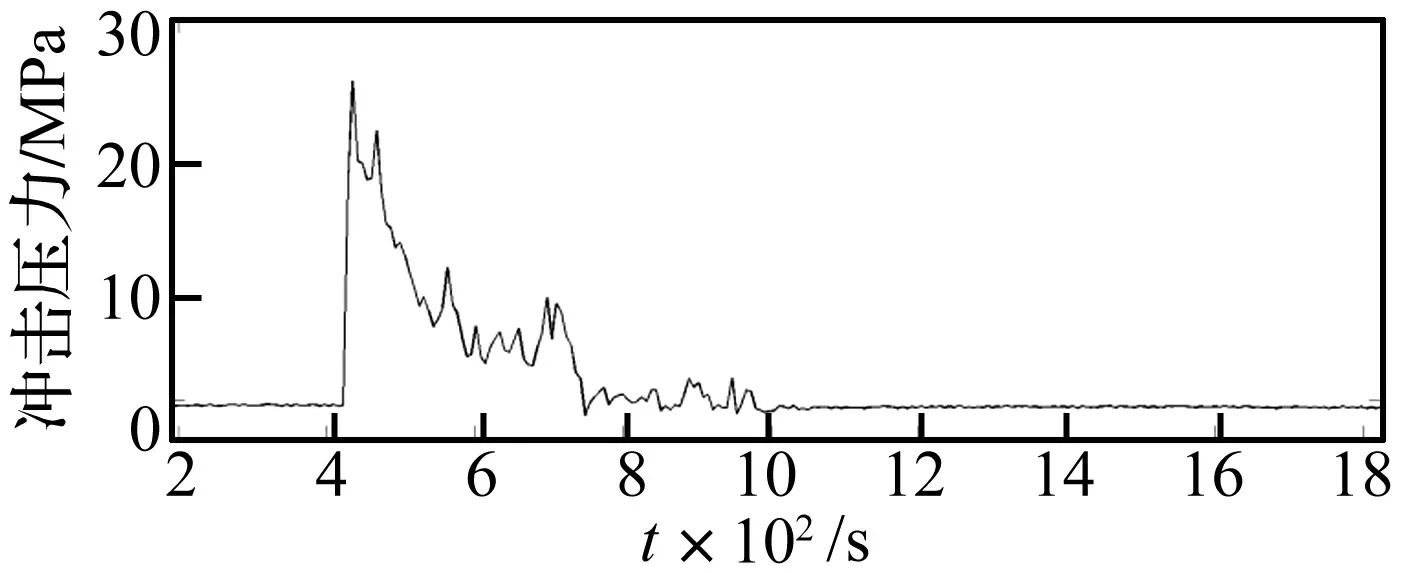
图4 传感器采集典型水冲冲击波压力曲线Fig. 4 Curve of typical flush water shock wave

3.1 软泥水底的冲击波峰值压力研究

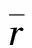
(16)

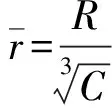
从图4可看出冲击波压力的变化比无限水中爆炸的冲击波压力衰减要复杂，由于水底和水面的作用，测点的冲击波波形衰减出现了明显的震荡，测点位置不同波形的震荡也不同。对冲击波波形影响的因素很多[14]，本文主要研究水深，测深，距离等几个因素对冲击峰值压力的影响，因此对测点波形变化的影响因素不做具体分析，主要对峰值压力进行采集并处理。

表1的数据利用最小二乘法，回归方程为

0.024X2+0.040X3-1.054X4

(17)

表2 F检验表

由表2可知,X4对Y的影响最为显著，其次是X1，再次是X2，而X3对Y的影响不显著。因此装药中心到测点的水平距离对入射波阵面峰值压力的影响最显著，其次是炸高，再次是测高，水深对入射波阵面峰值压力的影响不显著。去掉回归方程中含有X3的项，重新进行数据分析可得回归方程为

(18)

从能量分配的观点看，由于0.4 kg TNT集团装药等效装药半径为r=4 cm，试验水深H=47 cm。显然，H>7r，所以爆炸所产生能量主要用于形成水中冲击波和水底爆炸成坑，显然不会逸出水面，不会形成空气冲击波。文献[15]认为水深对测点峰值压力影响较小。在一定比例距离内，测高一定，炸高增加使相同比例距离的测点压力也增加。因此，浅水中爆炸试验条件下，流场测点的峰值压力可以不考虑水深影响。各自变量之间的相关性很小。因此软泥水底试验条件下，单个装药浅水中爆炸时，测点冲击波压力计算公式为

(19)

部分测点处的峰值压力回归计算与测点的实测峰值压力对比，结果如表3所示。依据回归公式计算得出的33个测点冲击波峰值压力与对应测点实测冲击波峰值压力之间的相对误差在0.48%～15.68%，其中相对误差超过15%的测点只有一个，该测点应视为奇异测试数据。因此利用回归公式反推测点的冲击波峰值压力，与对应测点的实测峰值压力比较，并结合测试波形的分析，可进一步剔除实测的奇异结果。相对误差在5%～10%的测点有8个，占据统计测点的24.2%，其余测点的误差均<5%，33组对比数据的平均误差值为4.34%。可见在该试验条件下，回归公式能够用于单个装药浅水中爆炸流场中冲击波峰值压力的计算，结果有较高的精度。

3.2 软泥夹石水底冲击波峰值压力研究

软泥夹石水底条件下，统计实爆模型试验中，爆炸流场中部分测点峰值压力的实测结果见附表2。利用最小二乘法，对附表2所列数据进行初步回归计算，通过F检验及分析可得水深因素X3对压力回归参量X5的影响不显著。因此，该试验条件下流场测点的冲击波峰值压力回归处理可以不考虑水深影响。

软泥夹石水底试验条件下，流场测点冲击波峰值压力计算公式为

(20)

比较相同测点回归公式的计算值与实测值可知见附表4，36个测点的实测值与计算值之间的相对误差在0.15%～21.33%，<5%的测点占29个，只有一个测点的相对误差超过20%，36组对比数据的平均误差值为3.54%，所以采用回归公式计算结果的精度较高。

3.3 水底介质对冲击波峰值压力影响的分析

假如爆炸能量不能被水底吸收，装药在水中沉底爆炸将等效于一个无限水中爆炸的双倍药包，假设能量都集中水里，作为近似值，双倍药包在任何距离上的峰值压力增加至1.26倍，持续时间和冲量也会增加而增加，炸高的影响大于测高的影响；测点峰值增加，能流密度增至2倍。然而水底不可能为刚性界面，必然会消耗吸收一部分爆炸能量，水底的介质不同，消耗的爆炸能量不同，由于水底和水面反射波的影响，水中冲击波的强度会小于双倍药包的近似值。根据近些年的试验研究，当装药置于近软泥水底处爆炸时，水底反射的首先不是冲击波(或者压缩波)，而是反射稀疏波；随着水底介质被压实，继而反射的才是反射压缩波[16]。水底对水中冲击波的影响同自由面正好相反，在水底泥层或者岩石层反射时，或者从其他巨大障碍物表面反射时，形成的是反射波与水中传播的波相互作用影响着冲击波峰值压力。

结合表1、表2的数据，将不同水底条件下，峰值压力pm的库尔公式分别为

软泥水底介质

(21)

软泥夹石水底介质

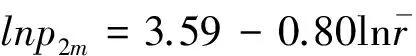
(22)

为了对不同水底介质对峰值压力的影响进行研究，在两种不同水底介质的浅水中进行试验，相同测点位置的峰值压力如表3所示。软泥夹石水底测点的峰值压力均大于软泥水底对应测点的峰值压力，表明水底介质越硬，装药浅水中爆炸载荷越大，有利于提高爆破破坏作用。

表3 两种不同水底介质峰值压力

根据表3实测数据，近似可得

3p2m=4p1m

(23)

经验式(16)计算和试验测点峰值压力的拟合曲线如图5所示，从图中可以看出软泥夹石水底试验条件下测点的峰值压力分布在距离理论计算值的近，对比两图可知软泥夹石水底测点在相同的比例距离上峰值压力要比软泥水底高，这是由于水底和水面的反射波对冲击波压力的切断以及相互作用不同而导致的差异。浅水中爆炸，相同试验条件下，软泥夹石水底冲击波峰值压力为软泥水底冲击波峰值压力的4/3倍。

(a) 软泥水底 (b) 软泥夹石水底图5 不同水底介质峰值压力拟合曲线Fig.5 Fitting curve of peak pressure of shock wave in different water bottom

分析实测值与回归分析结果可知，试验条件下的两种水底介质，测点冲击波峰值压力都随炸高和测高的压力随水平距离的增加而减少，这种影响远大于炸高和测高；水底影响的条件下，测点峰值压力均小于相同位置无限水中爆炸冲击波峰值压力值；软泥水底情况下测点峰值压力的幅值均小于软泥夹石水底相同测点的冲击波峰值压力，说明软泥水底吸收的爆炸能量更多，水底介质硬度越高，水冲冲击波峰值压力增加越多。

4 结 论

通过建立浅水中爆炸影响冲击波峰值压力因素的回归模型及分析方法，对各个影响因素进行分析，并通过试验数据对模型进行回归分析和检验，得出以下结论：

(1)通过回归模型得出的回归公式计算数据较为准确，相对误差较小，在公式适用范围内，计算结果有较高的精度。

(2)炸高、测高、水深及水平距离对水中测点冲击波峰值压力都有影响，其中装药中心到测点的水平距离对入射波阵面峰值压力的影响最显著，其次是炸高和测高，水深对入射波阵面峰值压力的影响不显著。

(3)水底介质硬度越高，冲击波压力峰值越大相同试验条件下，软泥夹石水底浅水中爆炸的冲击波峰值压力为软泥水底冲击波峰值压力的4/3倍。

[ 1 ] 顾文彬.浅层水中爆炸冲击波压力特性试验与数值模拟研究[R].博士后研究工作报告,解放军理工大学,2000.

[ 2 ] BJARNHOLT G.Suggestions onstandards for measurement and data evaluationin the underwater explosion test[J]. Propellants Explosives Pyrotechnics, 1980,5(2/3):67-74.

[ 3 ] HAMMOND L.Underwater shockwave characteristics of cylindrical charges[R].Defence Science and Technology Organisation, AMRL, DSTO-GD-0029.

[ 4 ] MICHAEL M,SWISDAK J. Explosion effects and properties: PartⅡ, explosion effects in water:AD-A056694[R].1978.

[ 5 ] 李澎,徐更光.水下爆炸冲击波传播的近似计算[J]. 火炸药学报,2006,29(4):21-24. LI Peng, XU Gengguang. Approximate calculation of underwater explosion shock wave propagation[J]. Chinese Journal of Explosives and Propellants, 2006,29(4):21-24.

[ 6 ] 李金河,赵继波,谭多望,等.炸药水中爆炸的冲击波性能[J].爆炸与冲击, 2009, 29(2): 172-176. LI Jinhe,ZHAO Jibo, TAN Duowang, et al. Underwater shock wave performances of explosives [J]. Explosion and Shock Waves, 2009, 29(2): 172-176.

[ 7 ] COLE R H, WELLER R.Underwater explosions[J].Physics Today,2009,1(6):35.

[ 8 ] ZAMYSHLYSAEV. Pressure fields during underwater explosion in a free fluid[J].Dynamic Loads in Underwater Explosion, 1973,7(2):86-120.

[ 9 ] 顾文彬,叶序双,刘文华,等. 界面对浅层水中爆炸冲击波峰值压力影响的研[J]. 解放军理工大学学报(自然科学版)，2001,2(5):61-63. GU Wenbin, YE Xushuang, LIU Wenhua, et al. Peak pressure investigation of exploding wave influenced by interfaces in shallow-layer water[J]. Journal of PLA University of Science and Technology,2001,2(5):61-63.

[10] 梁向前.水下爆破技术[M].北京：化学工业出版社，2013.

[11] 周霖,徐少辉,徐更光.炸药水下爆炸能量输出特性研究[J].兵工学报,2006,27(2):235-238. ZHOU Lin, XU Shaohui , XU Gengguang. Research on energy output characteristics for underwater explosion of explosives[J]. Acta Armamentarii,2006,27(2): 235-238.

[12] Л П 奥尔连科.爆炸物理学(上)[M].孙承纬,译.北京：科学出版社，2011:596-648.

[13] 张德丰. Matlab数字信号处理与应用[M]. 北京：清华大学出版社,2010:297-327.

[14] SAITO T, MARUMOTO M. Experimental and numerical studies of underwater shock wave attenuation[J]. Shock Waves,2013,13(2):139-148.

[15] 顾文彬,马海洋,唐勇,等. 水底对浅水中装药爆炸效果的影响[J].爆破,2003,20(4):88-92. GU Wenbin, MA Haiyang, TANG Yong, et al. Influence of water bottom on the explosion effect of shallow-layer water charging [J]. Blasting,2003,20(4):88-92.

[16] 叶序双.爆炸力学基础[M].南京：解放军理工大学工程兵工程学院,2004.

Experimental study on the influence of the bottom medium on the peak pressure of explosion shock waves in shallow water

WANGZhenxiong1,GUWenbin1,CHENJianghai1,XUJinglin1,LIUXin1,LUMing2

(1.College of Field Engineering, PLA University of Science and Technology, Nanjing 210007, China; 2. Wuhan Ordnance N.C.O school,Wuhan 430075, China)

Peak pressure of the shock wave in water, an important factor for evaluating shock wave intensity of the underwater explosion, is vital to relevant studies. Based on the similarity law of the explosion, this research makes a deduction on similar requirements of the simulation experiments of underwater explosion and establishes the regression model about peak pressure of the underwater shock wave under test condition. Simulated tests were carried out under the condition of two types of water bottom media and different water depths, then peak pressures of underwater blast wave at different measuring points were acquired. Through formula fitting of test data by the π theorem, dimensional analysis and the least squares, a formula consistent with similarity law of explosion was obtained. And the analysis on regression precision of formula verified its accuracy. Significance test indicates that the influence of distance between measuring points and charge on peak pressure of underwater blast wave is the largest while that of water depth is the least and can be ignored. With analysis on data from tests with different water media, it is concluded that water bottom mediums affect peak pressure more. And peak pressure of blast wave in test at the water bottom of soft mud with stones is about 4/3 times that of the water bottom of soft mud.

underwater explosion; shock wave; peak pressure; similarity theory; experiment study

总后基建营房部项目(BY209J033)

2015-10-10 修改稿收到日期：2016-02-23

王振雄 男，博士生，1987年6月生

顾文彬 男，教授，博士生导师，1961年12月生

TD235

A

10.13465/j.cnki.jvs.2017.04.038