基于声发射信号的滚动轴承外圈疲劳剥落故障双冲击特征提取

孙守保， 郭 瑜， 伍 星

(昆明理工大学 云南省高校振动与噪声重点实验室，昆明 650500)

基于声发射信号的滚动轴承外圈疲劳剥落故障双冲击特征提取

孙守保， 郭 瑜， 伍 星

(昆明理工大学 云南省高校振动与噪声重点实验室，昆明 650500)

疲劳剥落是引起滚动轴承失效的主要原因。跟振动信号一样，当滚道出现疲劳剥落故障时滚动体在进入和退出剥落区时的声发射信号也存在对应的两类不同冲击特征，称为双冲击现象。对双冲击特征的提取可实现双冲击间隔的有效测量。声发射信号具有对早期故障敏感、不易受噪声干扰等优点。采用将两类特征分离处理的方法，将声发射信号中两类冲击特征分为两部分，通过AR模型和最小熵解卷积滤波增强故障特征信号，和基于复Morlet小波的谱峭度图算法提取优化解调频带对应的包络信号，对包络信号相加并进行双冲击间隔测量。实验研究表明，该方法能够有效地分离出滚动轴承外圈疲劳剥落故障声发射信号中的双冲击特征。

声发射；滚动轴承；外圈疲劳剥落；双冲击；复Morlet小波

滚动轴承(本文后续文字中简称轴承)是旋转机械装置中应用最广泛的零部件之一,也是机器中最容易损伤的零部件之一，对其进行故障检测有重要意义。轴承运行中，循环应力的作用易导致点蚀和疲劳剥落故障[1]。当初期裂纹出现时，其仍可正常工作较长时间[2]。文献[3]中指出，当滚道出现剥落故障时，滚子经过剥落区时会产生双冲击现象，并且将滚子进入剥落区时所产生的振动信号定义为阶跃响应，滚子退出剥落区时所产生的振动信号定义为脉冲响应。如果能准确提取轴承疲劳剥落故障的双冲击特征，可实现在运行状态下估算剥落区宽度，并用于轴承的剩余使用寿命预测。现有对轴承双冲击现象的研究主要基于振动信号。近来，SAWALHI等采用将阶跃响应和脉冲响应分离处理的方法成功提取出了轴承外圈故障振动信号中的双冲击特征。

声发射信号最先被定义为材料内部表面材料变形或损伤时快速释放应变能所产生的弹性应力波。MBA[4]在研究中将其定义为两个表面相对运动时相互作用而产生的弹性应力波。据此，我们认为滚子经过剥落区时分别作用于剥落区前沿和后沿也将产生与振动双冲击现象类似的声发射信号，本文将其分别记作进入响应和退出响应，但相关研究未见报道。与振动信号相比，声发射信号具有以下优点[5]：对早期故障更敏感，不易受机械背景噪声(<20 kHz)影响，并且对故障位置更敏感。基于这些优点，声发射信号在滚动轴承故障诊断技术中的应用越来越广泛[6]。本文同样采用分离处理方法，首先将声发射信号中的进入响应和退出响应分开，然后分别通过AR(Autoregressive Model)模型和最小熵解卷(Minimum Entropy Deconvolution, MED)滤波增强故障特征信号，再通过复Morlet小波构建滤波器树提取最优频带特征信号，最后对两个特征信号进行包络和标准化处理并相加即可提取得到双冲击特征。研究表明，该方法能够有效地分离出滚动轴承外圈疲劳剥落故障声发射信号中的双冲击特征。

1 轴承疲劳剥落故障双冲击现象

1.1 振动信号双冲击现象研究简介

EPPS[7]首次论述了轴承疲劳剥落故障的双冲击现象，在其研究中，提出了滚子在通过剥落区时会产生进入和退出两个事件，并在振动信号中明确指出进入和退出事件的起始点。滚动体在通过剥落区时产生双冲击现象示意图如图1所示(其中FN为滚动体所受滚道作用力;V为滚动体运动的切向速度)，由图1(a)和图1(b)为进入事件，其中A为进入点；由图1(b)和图1(c)为退出事件，其中B为退出点。DOWLING[8]在其研究中认为进入事件和退出事件均为脉冲响应，并且指出退出点相对于进入点存在180°相位变化。

图1 滚动体通过剥落区双冲击现象生成示意图Fig.1 Schematic of the generation of double impulse phenomenon

SAWALHI等明确提出了双冲击现象的概念，并且将进入事件定义为阶跃响应，退出事件为脉冲响应。如图1所示，自A点开始滚动体进入剥落区过程中，滚动体受力FN逐渐减小，方向由剥落区边缘指向滚动体中心，进入事件是一个较平缓的去应力过程，因此产生阶跃响应；当滚子到达B点时，滚子突然受到与运动方向相反的作用力FN(见图1(b))，激发冲击振动，因此退出事件产生脉冲响应。 SAWALHI等还阐述了阶跃响应主要包含低频成分，冲击响应则具有较宽的频带，并根据这两个特点提出了分离处理的方法使得两个特征信号在提取过程中都得到较好的增强。值得指出的是，以往研究均是基于振动信号进行的。

1.2 声发射信号双冲击现象

虽然现有研究中已有学者将声发射信号应用于轴承故障诊断的研究中，但未见关于声发射信号双冲击特征提取的相关报道。本文研究中采用与振动信号对比的方法调查研究声发射信号中的双冲击现象。

为方便比较，实验中，声发射传感器和振动加速度传感器安装在轴承座同一位置，以相同的采样率(1 MHz)同步采集声发射信号和振动信号(注：振动信号所需采样率远低于声发射信号所需采样率，研究中为比较方便使用同样采样率)。故障轴承外圈疲劳剥落宽度为2 mm，在转速为500 r/min下采集到的两类信号如图2所示，图2(a)为振动信号，图2(b)为声发射信号。

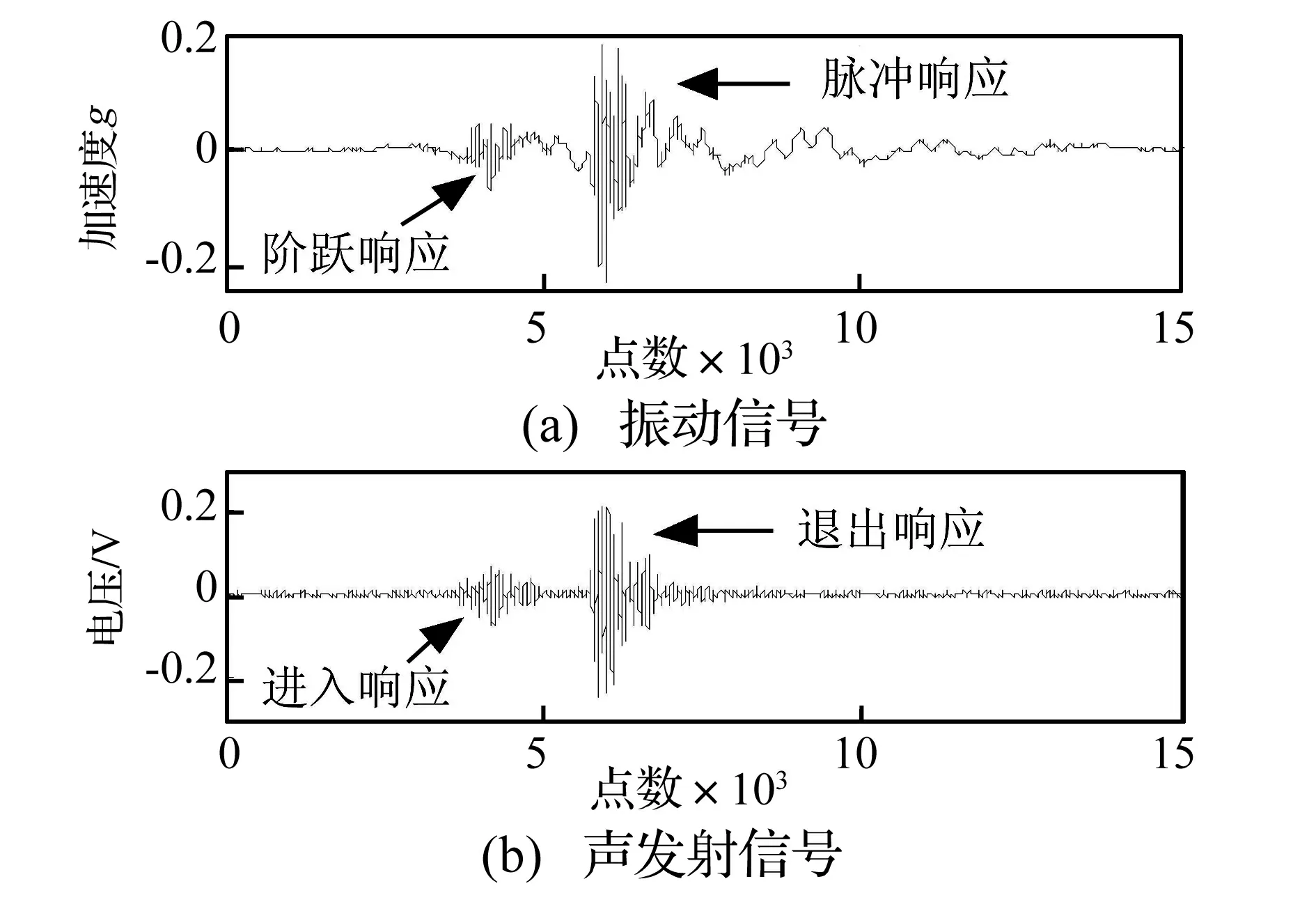
图2 外圈剥落故障(2 mm宽)球轴承信号Fig.2 Detected signal of outer race spalled ball bearing with fault width 2 mm

比对图2(a)和图2(b)可知，在振动信号中阶跃响应和脉冲响应出现的位置在声发射信号中存在对应的进入响应和退出响应。因此，外圈疲劳剥落故障轴承对应声发射信号也同样存在双冲击现象，但在波形上两者有较大差异。

2 双冲击特征增强与提取方法

2.1 分离提取方法

虽然外圈故障轴承声发射信号中的进入和退出双冲击特征都类似脉冲响应，但无论在幅值上还是频谱上二者存在较大差别。本文采用分离提取方法提取声发射信号中的双冲击特征，该方法在使用同一增强提取算法计算时可选取不同的参数分别处理进入和退出响应，使其都能得到较好的增强。其算法流程图如图3所示。分离提取方法主要步骤包括：①通过峰值搜索获取声发射信号中双冲击特征的峰值位置；②设置阈值为20%，将每组双冲击两个峰值之间采样点距离第二个峰值20%处作为分离参考点；③在分离参考点右侧到下一个参考点之间50%～80%的采样点数置零得到进入响应信号；④用原信号减去进入响应信号可得到退出响应信号。

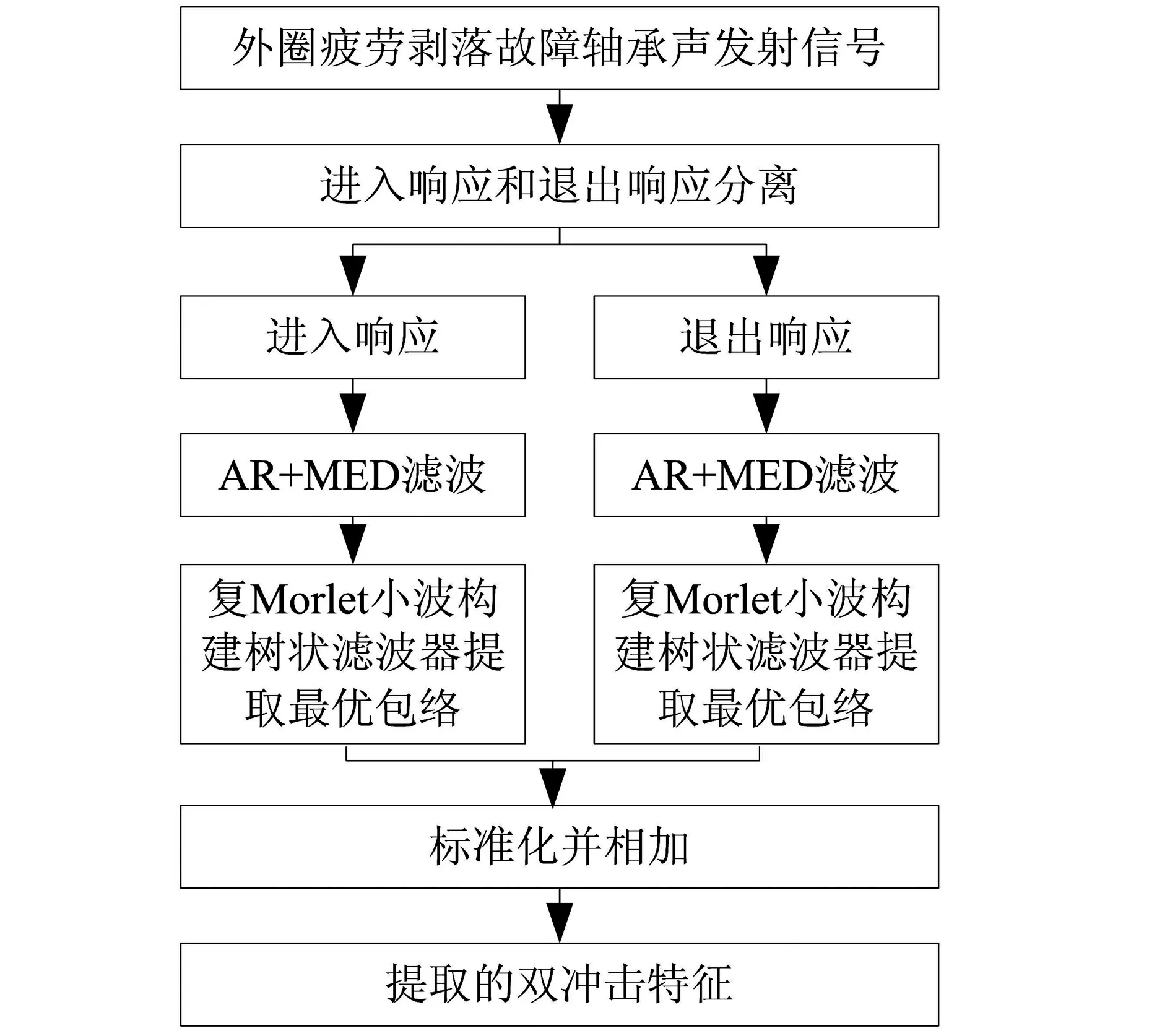
图3 双冲击特征增强和提取流程图Fig.3 Schematic of separation scheme to enhance and extract the double impulses

2.2 AR模型和MED的冲击成分增强

对分离后的信号分别用AR模型和MED滤波增强轴承故障特征信号。SAWALHI等[9-10]结合AR模型和MED有效增强了轴承故障特征信号，为轴承故障监测提供了便利。基于AR模型滤波的预白化过程可以提高声发射信号中冲击性成分的信噪比。设采集得到的轴承声发射信号记作xt，则预白化过程可表示为[11]

(1)

式中:et为AR模型残余信号，主要包含疲劳剥落故障引起的冲击性信号成分和加性白噪声;xt和xt-j分别为声发射信号序列在时间t和t-j点处的值;P为AR模型阶数;aj为自回归加权参数。预白化后得到残余信号et，去除了信号中的确定性成分，提高了信噪比。

MED能有效在混合信号中解卷出冲击性源[12-13]。而轴承发生故障时产生的振动通常具有冲击特征，因此MED适合对双冲击特征提取的前期降噪处理，其原理是寻找一逆滤波器(记作ft)将信号中的冲击源信号解卷出来。设et经过MED滤波后的信号为yt，则有

yt=(gt+nt)*ht*ft

(2)

式中:gt为轴承故障冲击源信号;nt为噪声干扰;*为卷积运算符；ht为传递路径影响。则yt可近似表示为

yt≈gt

(3)

为使yt尽可能的接近gt，MED参数(滤波器长度和迭代次数)的确定显得尤为重要。本文采用目标函数法(Objective Function Method, OFM)寻找使MED滤波器输出信号yt峭度值最大(使熵最小)的滤波器参数。目标函数法的实施是通过改变MED滤波器长度和计算迭代次数，其中使yt峭度值最大的滤波器长度和迭代次数将作为最优滤波器参数进行进一步计算。

2.3 基于复平移Morlet谱峭度图的包络提取

通过复Morlet小波构建滤波器组可分别提取进入和退出响应的优化包络。复Morlet小波定义为[14]

(4)

式中:σ为波形参数;f0为调制频率;j为虚数符号。其傅里叶变换式为

Ψ(f)=Ψ*(f)=e-(π/σ)2(f-f0)2

(5)

式中:Ψ(f)为ψ(t)的傅里叶变换;*为共轭；因为Ψ(f)为实数，所以Ψ(f)=Ψ*(f)；从滤波器的观点出发，复Morlet小波可看作以σ为带宽，f0为中心频率的滤波器。根据欧拉公式ejt=cos(t)+jsin(t)，式(4)可表示为

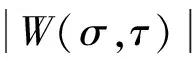
(7)

若将式(5)中的f0替换为不同中心频率fm，则可构建复平移Morlet小波树状滤波器，其频域表示为

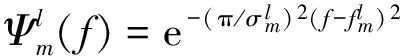
l=(1,2,…,L),m=(1,2,…,M)

(8)

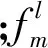
(9)

由式(7)和式(8)得基于复平移Morlet小波的树状滤波器信号包络提取可表示为[15]

(10)

在计算获得不同频带的包络信号后，通过谱峭度[16]，其计算如下

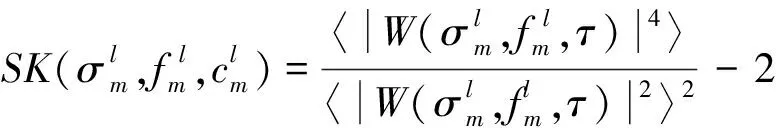
(11)

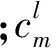
通过搜索最大单位带宽谱峭度可得到优化解调频带和对应的平方包络，其过程可表示为[17]

(12)

式中:σo为最优频带带宽;fo为最优频带中心频率;co则为提取的最优频带相应的最优平方包络;argmax为获取最大谱峭度对应的频带参数运算。

通过复Morlet小波构建树状滤波器组分别提取进入响应和退出响应最优包络信号。然后将其标准化并相加即可得到提取的双冲击特征。

3 实验研究

3.1 测试设备

研究中所提声发射信号双冲击提取方法在QPZZ-Ⅱ型故障模拟实验台(见图4(a))对实际模拟轴承外圈剥落故障进行了验证。试验台由三相交流电动机变频调速驱动，在轴承座附近有螺旋加载装置，可模拟轴承实际工作时的负载情况。试验中，声发射传感器安装在故障轴承所在轴承座上，如图4(b)所示。实验对象选择深沟球轴承(型号为6205)，外径52 mm，内径25 mm，具有9个滚动体。图4(c)展示了模拟加工的轴承外圈疲劳剥落故障，所示故障沿滚道方向(即宽度)尺寸为2 mm，深度为1 mm。声发射传感器和放大器分别选用WD型宽频传感器和配套前置放大器。数据采用 ADLINKPCI-9846H高速采集卡采集。试验时，转速调整为500 r/min，采样率Fs=1 MHz采集得到的声发射信号如图2(b)所示。

图4 测试设备Fig.4 Test equipment

3.1 数据分析

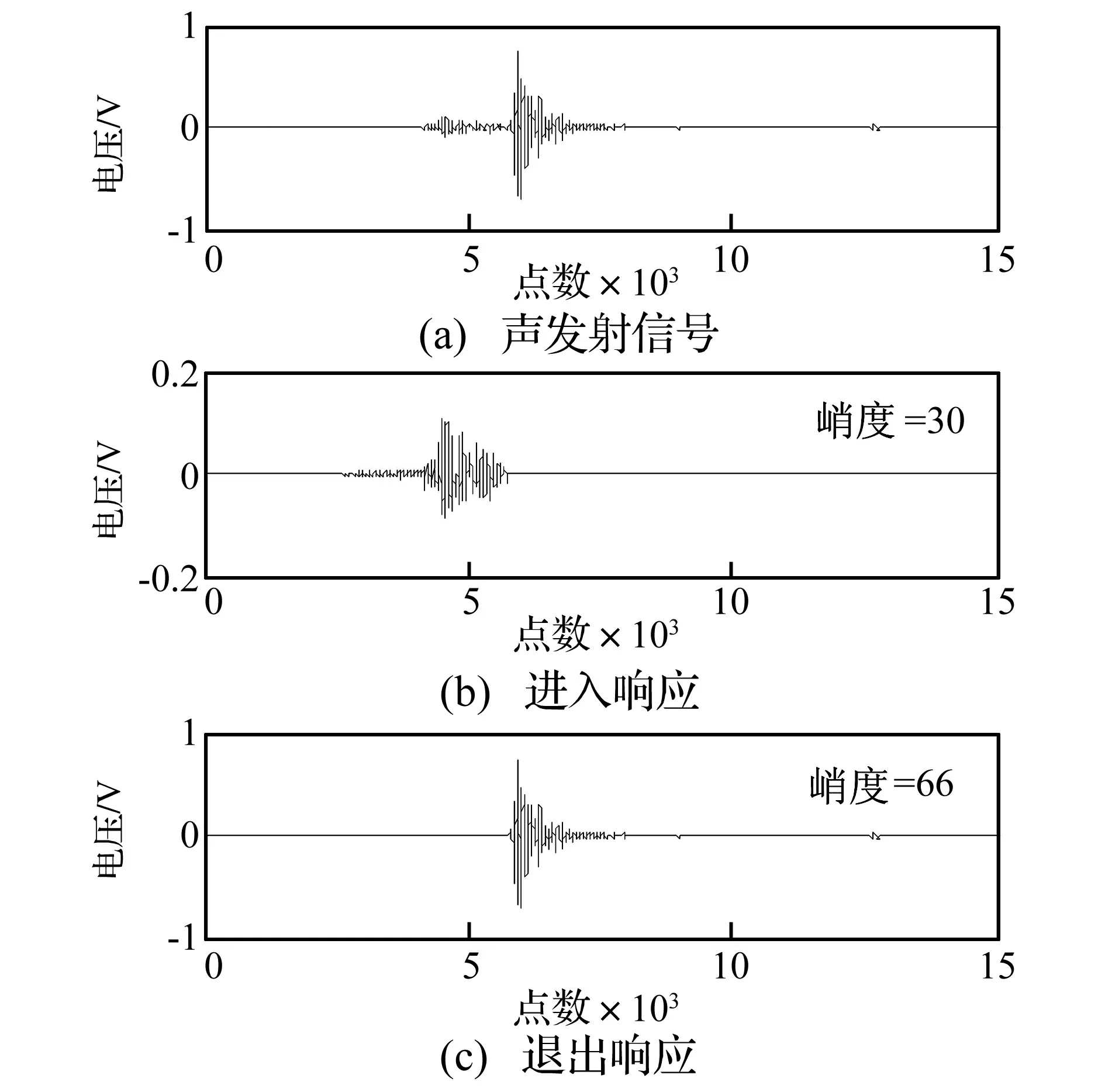
图5 信号分离Fig.5 Signal separation

采用图3所示方法首先将声发射信号中的进入和退出响应信号分离，结果如图5所示。图5(a)中所示进入响应信号相对退出响应信号较弱。分离后进入响应信号信噪比得到提高。分别对分离的进入和退出响应进行AR和MED滤波，得到特征增强的进入和退出响应分别如图6(a)和6(b)所示。与图5比较可知，两信号的峭度值得到较大提升，说明信号中的冲击成分得到增强，即两信号中的特征信号都得到了增强。

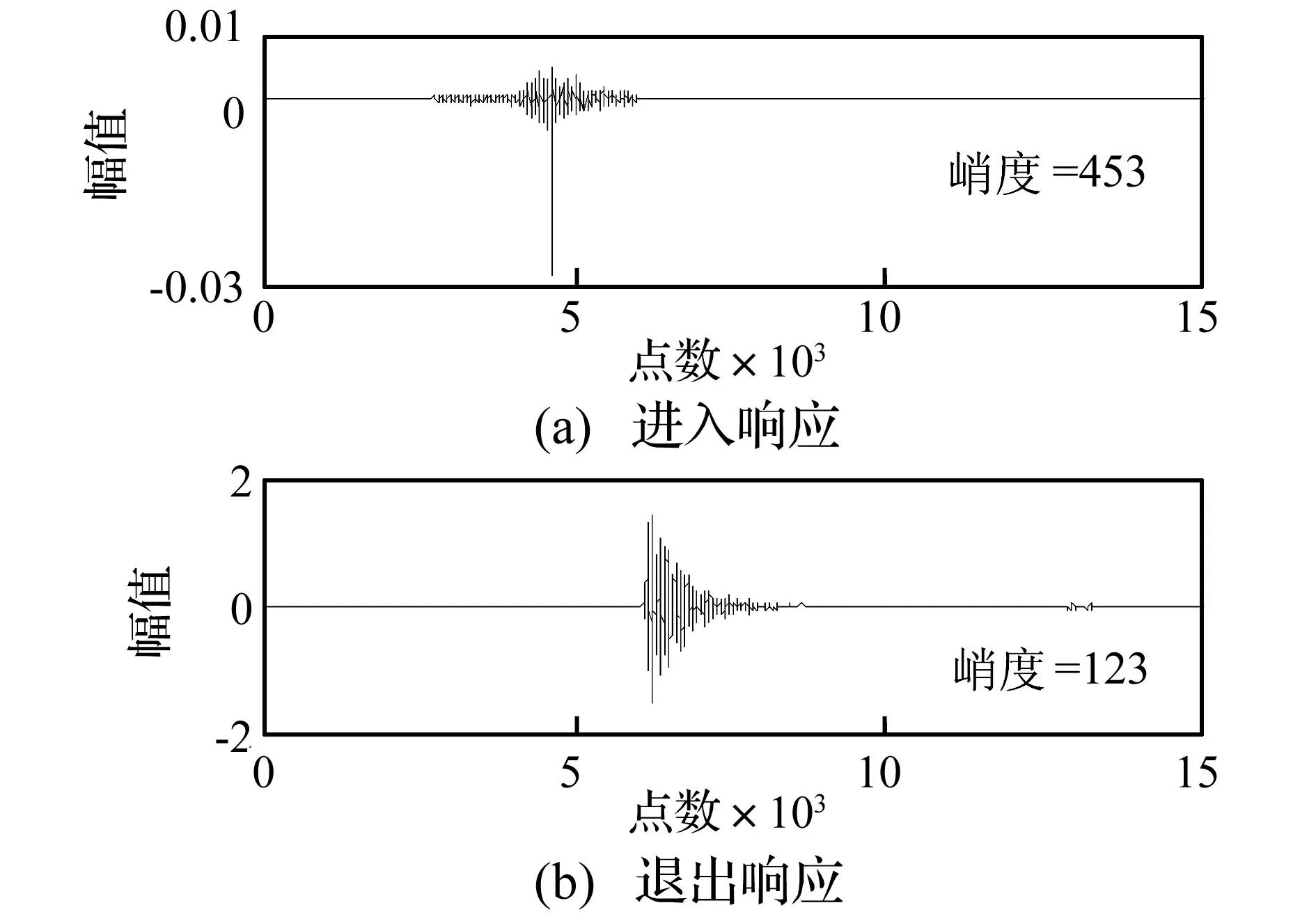
图6 AR和MED滤波处理结果Fig.6 AR and MED filter results

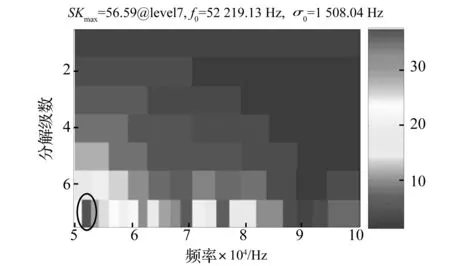
图7 进入响应谱峭度图Fig.7 SK of entry response

本研究中，复Morlet小波树状滤波器组的构建选择L=7级，k(l)=1, 2, 3, 4, 6, 12, 24及分析频带的倍频程数N=3。将通过AR和MED增强的进入响应信号和退出响应信号分别进行复Morlet小波滤波，进入响应和退出响应的谱峭度图分别如图7、图8所示。由于采样率高达1 MHz，为清晰显示分析结果，谱峭度图中频率轴上限设置为100 kHz，由图7和图8可见，进入响应信号和退出响应信号的最优频带(椭圆标记位置)的中心频率和带宽分别为(52 219.13 Hz, 1 508.04 Hz)和(62 099.36 Hz, 1 793.38 Hz)，最优频带对应的包络即最优包络。分别提取进入响应信号和退出响应信号的最优包络并标准化，最后将两者相加即得到双冲击特征信号，如图9所示。其中，图9(a)所示为标准化的进入响应特征信号，图9(b)为标准化的退出响应特征信号，图9(c)则表示提取的双冲击特征。研究表明，所述基于复Morlet小波滤波的方法可有效提取声发射信号中的双冲击特征。

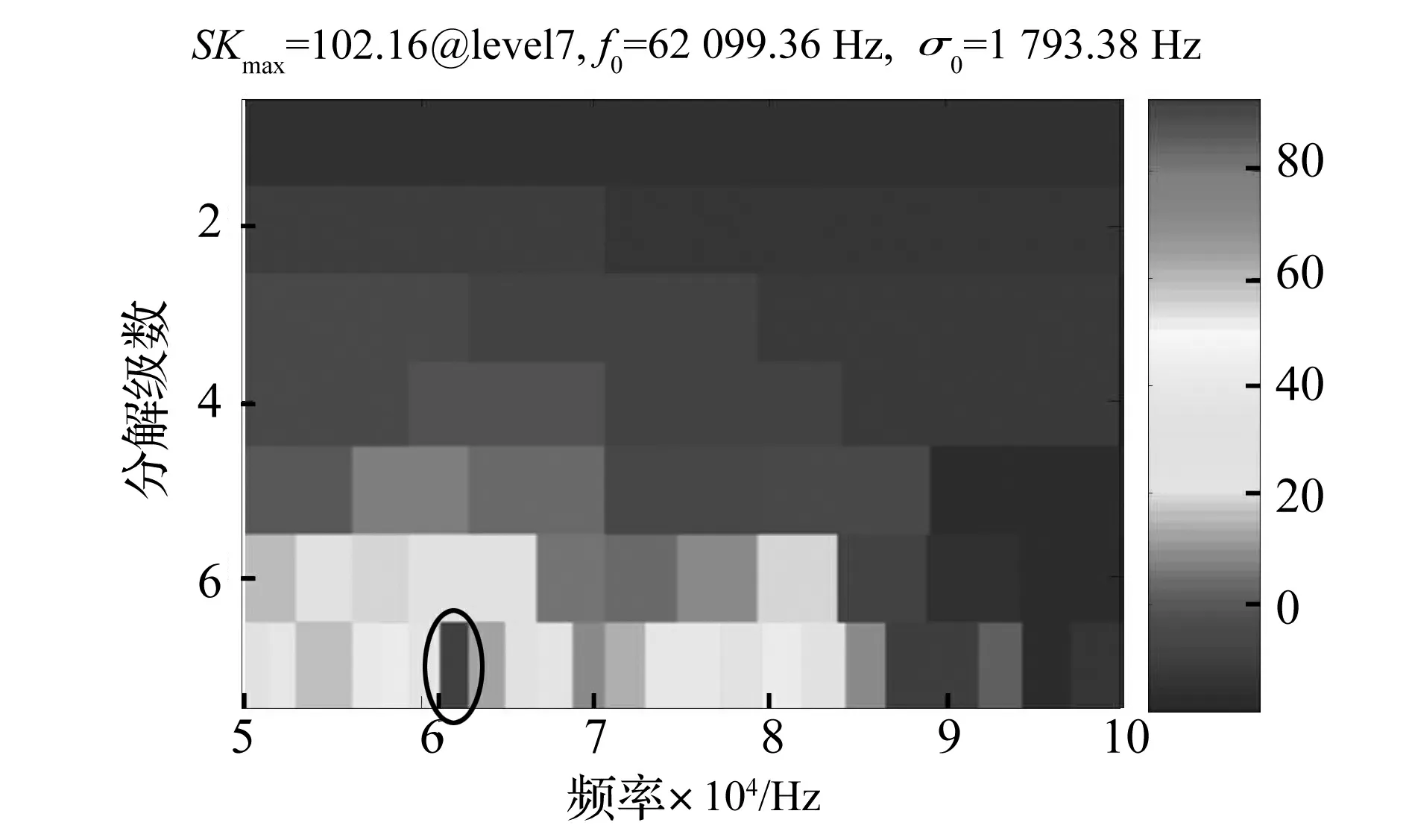
图8 退出响应谱峭度图Fig.8 SK of exit response

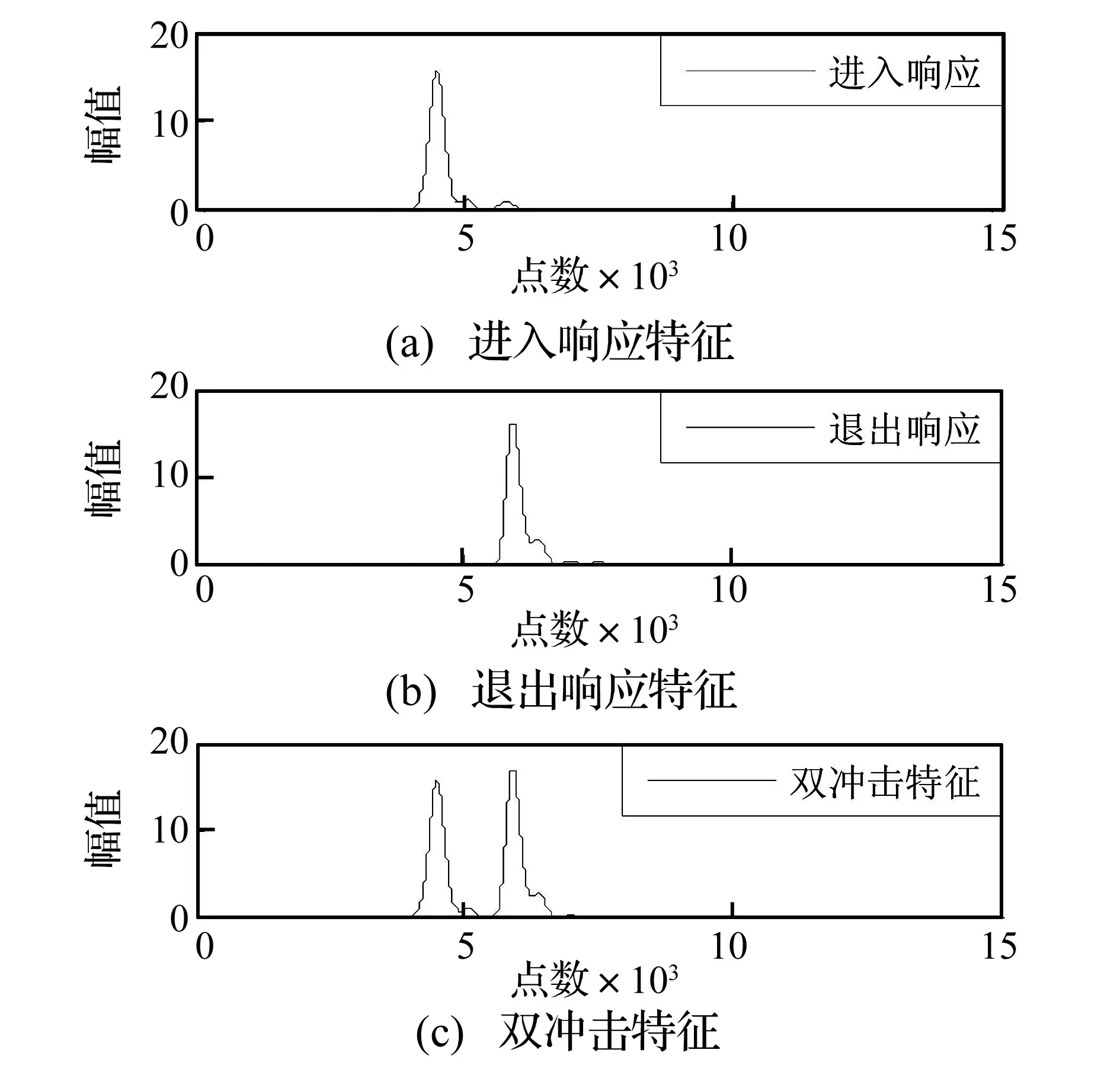
图9 提取的双冲击特征Fig.9 Extracted double impulses

4 双冲击特征提取应用研究

提取的双冲击特征可用于实现故障区(剥落区)尺寸估算，并进一步用于轴承剩余使用寿命预测。双冲击是滚动体经过剥落区，分别与剥落区前后边缘作用而产生的，因此其与故障区尺寸大小和转轴转速有关。根据双冲击间的采样点数和对应的采样率可计算得到双冲击的时间间隔，再结合转速即可估算滚动体所通过故障区的尺寸。

运用前文所述方法分别对转速为300 r/min，外圈故障尺寸分别为0.93 mm、1.24 mm、1.54 mm和2 mm的轴承声发射信号进行双冲击特征提取，结果如图10所示。

故障尺寸与双冲击间采样点数关系如图11所示。可见，在相同转速下随着故障尺寸的增大双冲击间数据点数有增多的趋势，但并非线性关系。为考察转速和双冲击的关系，同样使用本方法对外圈故障尺寸为2 mm，不同转速(300 r/min、400 r/min、500 r/min、600 r/min、700 r/min)下的轴承声发射信号分析结果如图12所示，随着转速的增加，双冲击间的数据点数减少，二者关系曲线如图13所示。结果初步表明双冲击间距与故障区尺寸和转速相关联，但并非简单的线性关系，后续工作中将对此进行深入研究。

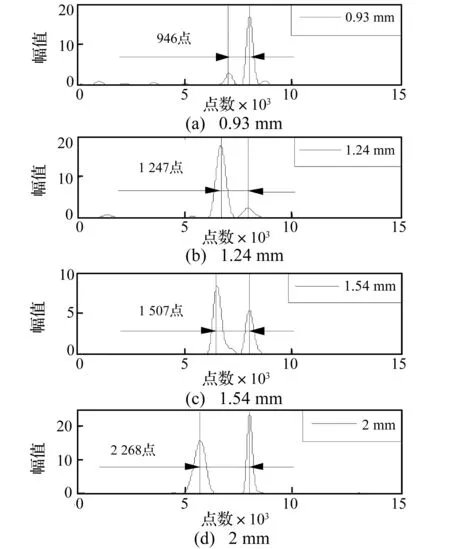
图10 在300 r/min转速下提取的不同尺寸轴承外圈故障双冲击特征Fig.10 Extracted double impulses of different fault sizes at 300 r/min

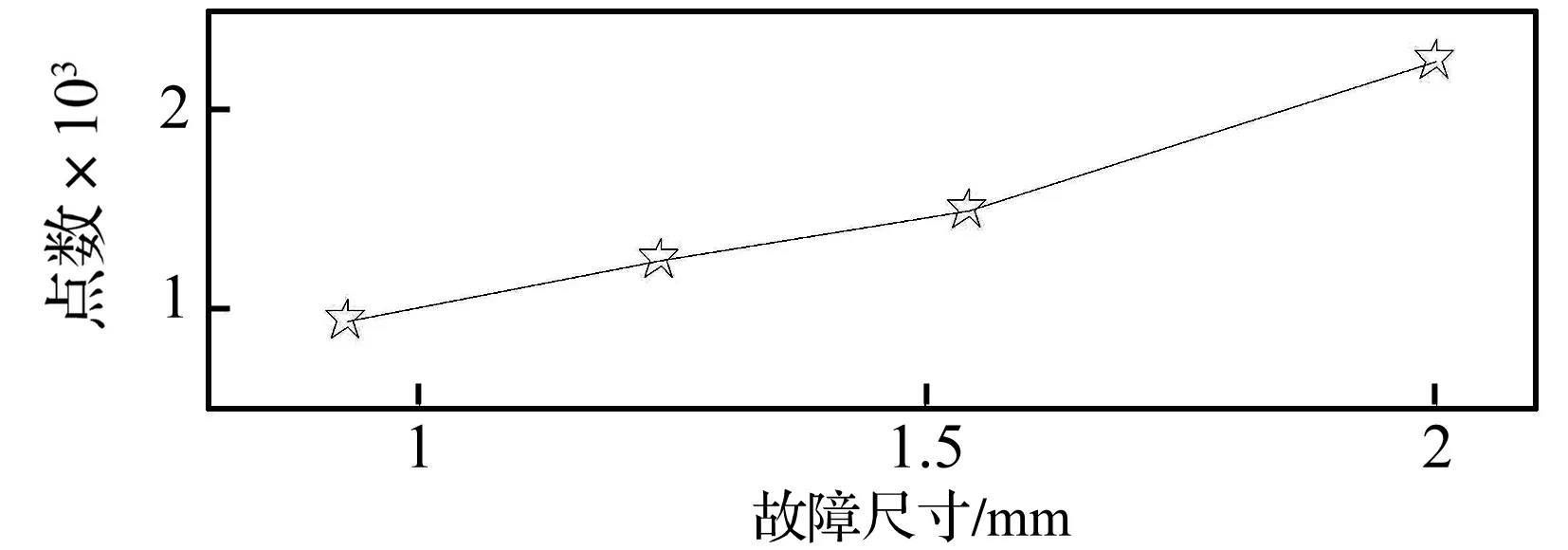
图11 在300 r/min转速下故障尺寸与双冲击间数据点数关系曲线Fig.11 Relationship of fault sizes and samples between the double impulses at 300 r/min

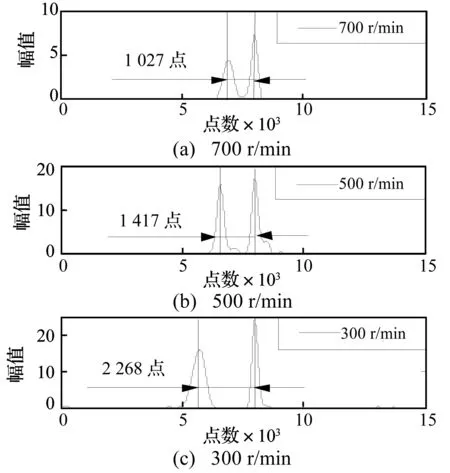
图12 在不同转速下提取的2 mm轴承外圈故障双冲击特征Fig.12 Extracted double impulses of different shaft speeds with fault width 2 mm

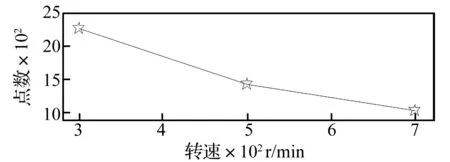
图13 2 mm故障轴承转速与双冲击间采样点数关系曲线Fig.13 Relationship of shaft speeds and samples between the double impulses with fault width 2 mm

5 结 论

实验研究表明，轴承外圈剥落故障声发射信号存在双冲击现象。AR模型和MED滤波可有效增强轴承故障特征信号。文中所述分离处理和基于复Morlet小波的特征信号提取方法可有效提取声发射信号中的双冲击特征，为进一步研究基于双冲击特征的剥落区估计奠定了基础。同时也丰富了现有基于声发射信号的轴承故障诊断方法。

[ 1 ] KUHNELL B T. Wear in rolling element bearings and gears—How age and contamination affect them[J]. Machinery Lubrication, 2004(9):62-64.

[ 2 ] SAWALHI N,RANDALL R.Vibration response of spalled rolling element bearings: observations, simulations and signal processing techniques to track the spall size[J].Mechanical Systems and Signal Processing, 2011,25(3):846-870.

[ 3 ] MATTHEWS J R. Acoustic emission[M].Boca Raton:CRC Press, 1983.

[ 4 ] MBA D.The use of acoustic emission for estimation of bearing defect size[J]. Journal of Failure Analysis and Prevention, 2008,8(2):188-192.

[ 5 ] LI R, HE D.Rotational machine health monitoring and fault detection using EMD-based acoustic emission feature quantification[J].Instrumentation and Measurement, 2012,61(4):990-1001.

[ 6 ] HEMMATI F, ALQARADAWI M, GADALA M S.Rolling element bearing fault diagnostics using acoustic emission technique and advanced signal processing[J].ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2015,5(9):1628-1636.

[ 7 ] EPPS I.An investigation into vibrations excited by discrete faults in rolling element bearings[D]. Christchurch:University of Canterbury Mechanical Engineering,1991.

[ 8 ] DOWLING M J.Application of non-stationary analysis to machinery monitoring[C]// New York:ICASSP IEEE Computer Society, 1993:59-62.

[ 9 ] SAWALHI N, RANDALL R, ENDO H.The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J]. Mechanical Systems and Signal Processing, 2007,21(6):2616-2633.

[10] SAWALHI N.Diagnostics, prognostics and fault simulation for rolling element bearings[D].Sydney: The University of New South Wales Australia, 2007.

[11] CHENG Junsheng, YU Dejie, YANG Yu.A fault diagnosis approach for roller bearings based on EMD method and AR model[J].Mechanical Systems and Signal Processing, 2006,20(2):350-362.

[12] LEE J Y,NANDI A.Extraction of impacting signals using blind deconvolution[J]. Journal of Sound and Vibration, 2000,232(5):945-962.

[13] 刘志川, 唐力伟, 曹立军.基于 MED 及 FSK 的滚动轴承微弱故障特征提取[J]. 振动与冲击,2014,33(14):137-142. LIU Zhichuan, TANG Liwei, CAO Lijun.Feature extraction of rolling bearing’s weak fault based on MED and FSK[J]. Journal of Vibration and Shock, 2014,33(14):137-142.

[14] SAWALHI N,RANDALL R B.Spectral kurtosis optimization for rolling element bearings[C]//Sydney:The 8th International Symposium on Signal Processing and its Applications, 2005:839-842.

[15] 郭瑜, 郑华文, 高艳, 等.基于谱峭度的滚动轴承包络分析[J]. 振动、测试与诊断,2011,31(4): 517-521. GUO Yu, ZHENG Huawen, GAO Yan, et al. Envelope analysis of rolling element bearing based on kurtogram[J]. Journal of Vibration, Measurement & Diagnosis,2011,31(4): 517-521.

[16] ANTONI J,RANDALL R.The spectral kurtosis: a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing, 2006,20(2):282-307.

[17] GUO Y, NA J, LI B, et al.Envelope extraction based dimension reduction for independent component analysis in fault diagnosis of rolling element bearing[J].Journal of Sound and Vibration, 2014, 333(13):2983-2994.

Double impulse phenomenon extraction of outer race spalled rolling element bearings based on acoustic emission signals

SUNShoubao,GUOYu,WUXing

(Key Laboratory of Vibration & Noise under Ministry of Education of Yunnan Province, Kunming University of Science and Technology, Kunming 650500, China)

Spalling is a major type of fatigue failures of rolling element bearings (REB). As the double impulses phenomenon can be observed in the vibration when a rolling element is entering or exiting the spall in the outer race or the inner race of the faulty REB, the double impulses phenomenon can be also observed in the acoustic emission (AE) signals generated by the faulty REB. If the space between the double impulses can be measured accurately, the width of the spall may be estimated. It will be helpful on the evaluation of remaining useful life (RUL) of REBs. The AE signal is more sensitive to the incipient fault and better to realize interferences isolation. Then, the separate treatment is used to extract the double impulses from the AE signal in this paper. In the proposed scheme, the AE signal was separate into two parts (the entering part and the exiting part) at first. Then the autoregressive model and the minimum entropy deconvolution method were used to enhance the two parts, respectively. After that, the complex Morlet wavelet based kurtogram were utilized to extract the optimal envelope, respectively. At last, the extracted envelopes were added together for the space measurement of the two impulses. Experiment analysis indicates that, the double impulse phenomenon can be effectively extracted in the AE signals of outer race spalled rolling element bearings.

acoustic emission; rolling element bearing; outer race spalling; double impulse phenomenon; complex Morlet wavelet

国家自然科学基金(51365023)

2015-10-15 修改稿收到日期：2016-01-10

孙守保 男，硕士，1990年生

郭瑜 男，教授,博士生导师，1971年生 E-mail: kmgary@163.com

TH133.3

A

10.13465/j.cnki.jvs.2017.04.001