双分裂导线尾流诱发振荡数值模拟研究

何小宝， 严 波,2， 伍 川， 张 博， 杨晓辉

(1.重庆大学 航空航天学院，重庆 400044；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044； 3.河南省电力公司电力科学研究院，郑州 450052；4.国家电网公司输电线路舞动仿真技术重点实验室，郑州 450052)

双分裂导线尾流诱发振荡数值模拟研究

何小宝1， 严 波1,2， 伍 川1， 张 博3,4， 杨晓辉3,4

(1.重庆大学 航空航天学院，重庆 400044；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044； 3.河南省电力公司电力科学研究院，郑州 450052；4.国家电网公司输电线路舞动仿真技术重点实验室，郑州 450052)

利用Fluent流体动力学软件模拟双分裂导线绕流场，计算两根子导线的空气动力系数，得到背风侧子导线的升力系数和阻力系数随其与迎风侧子导线相对位置的变化规律。进而利用ABAQUS软件模拟典型双分裂线路段的尾流诱发振荡过程，获得两根子导线的运动轨迹、振动幅值和频率特征。结果表明，两子导线的位移相位相反，运动轨迹近似为水平椭圆，与现场观测一致。模拟分析了间隔棒等间距和非等间距排布方式下双分裂导线尾流诱发振荡的特征。

双分裂导线；空气动力系数；尾流诱发振荡；数值模拟

当风场中分裂导线的背风侧子导线位于迎风侧子导线的尾流驰振区时，可能会发生气动失稳，诱发尾流驰振。分裂导线尾流驰振包括水平舞动、垂直舞动、扭转振动和次档距振动等[1]，其中次档距振动为主要形式。根据对二分裂和四分裂导线观察表明:次档距振动频率约为1～3 Hz，振幅约为0.1～0.5 m，子导线的运动轨迹一般呈水平扁长椭圆。导线尾流驰振严重时会造成子导线间相互碰撞，产生“鞭击”现象，甚至引起金具的破坏，对线路的安全运行造成严重威胁。

尾流区中子导线的气动特性是研究分裂导线尾流驰振的基础。PRICE[2]利用风洞试验测量了光滑和胶股双分裂导线在两种湍流度、不同雷诺数下背风侧子导线的升力系数和阻力系数与其在尾流区中位置的关系，但测量的位置限制在较窄的范围内。DIANA等[3]在风洞中通过按次档距振动时导线可能的运动形式来移动导线圆柱模型，测量了光滑和胶股双圆柱的气动参数，考虑了不同风速下导线移动频率和幅度对气动参数的影响。陈元坤[4]利用计算流体动力学方法，计算了不同雷诺数下双分裂导线绕流场，研究了子导线间距、湍流强度、雷诺数等对背风侧子导线气动系数的影响，但没有给出子导线气动参数在整个尾流区中的变化规律。

自20世纪70年代，分裂导线尾流驰振问题在国际上就引起关注，但公开报道的研究成果较少。WARDLAW等[5]利用风洞试验测量了光滑和绞股子导线尾流区稳定边界，研究了分裂导线间距和湍流对稳定边界的影响，并建立理论简化模型分析了次档距振动特征。TSUI等[6]利用有限元方法模拟了双分裂导线尾流驰振问题，指出使用三维模型的必要性。HARDY等[7]通过大量现场观测，研究了分裂导线尾流诱发振荡特征，并分析了风向、导线张力、子导线排列方式、间隔棒排布方式和数目等对尾流驰振的影响。YANG等[8]给出了计算分裂导线次档距振动极限幅值和最大次档距间距的方法。李黎等[9]采用稳定性理论利用二维振子模型研究了双分裂导线次档距振荡的机理。最近，本文作者课题组[10]对四分裂导线的尾流弛振进行了数值模拟研究，但忽略了背风侧子导线气动系数随其在尾流区中位置变化的影响，模拟得到的导线运动轨迹与现场观测结果存在较明显的差异，存在不足。

本文首先利用Fluent流体动力学软件模拟双分裂导线的绕流场，获得双分裂导线气动系数随两子导线相对位置的变化规律。利用ABAQUS有限元软件建立典型双分裂线路的三维有限元模型，模拟研究双分裂导线的尾流诱发振荡过程，分析次档距振动的特征，以及间隔棒等间距和非等间距两种安装方式对次档距振动的影响。本文方法和获得的结果，对双分裂导线次档距振荡抑制方法和技术的研究具有重要的参考价值。

1 导线空气动力特性数值模拟

1.1 绕流场数值模拟

目前，关于导线次档距振动和舞动等问题的研究，导线气动参数的数值模拟和风动试验大都采用准静态方法，已有的研究表明，采用准静态气动参数能够反映导线的主要运动特征。因此，本文仍采用准静态分析方法。

已有的研究表明，迎风侧子导线产生的尾流区边界与尾流中心线的夹角约为±20°。假设子导线直径为D，迎风侧子导线对背风侧子导线气动特性的影响区域在流动方向约为50D[11]，而在垂直于流动方向的影响范围与其水平间距有关，一般认为在±5D范围内影响最大[12]。

本文流场计算模型中，两根子导线水平间距范围取4D～50D，垂直间距范围取-5D～5D。分析的子导线直径为27.6 mm，尾流影响区域及计算模型参见图1。计算来流为稳定流，风速为12 m/s。

湍流模型选择Spalart-Allmaras模型[13]，采用有限体积法，增量步为0.001 s。其中左边界为速度入口，右边界为压力出口，上下边界为对称边界。模拟双分裂导线不同间距的绕流场时，迎风侧子导线位置固定，通过改变间距Y和Z来改变两根子导线之间的距离。

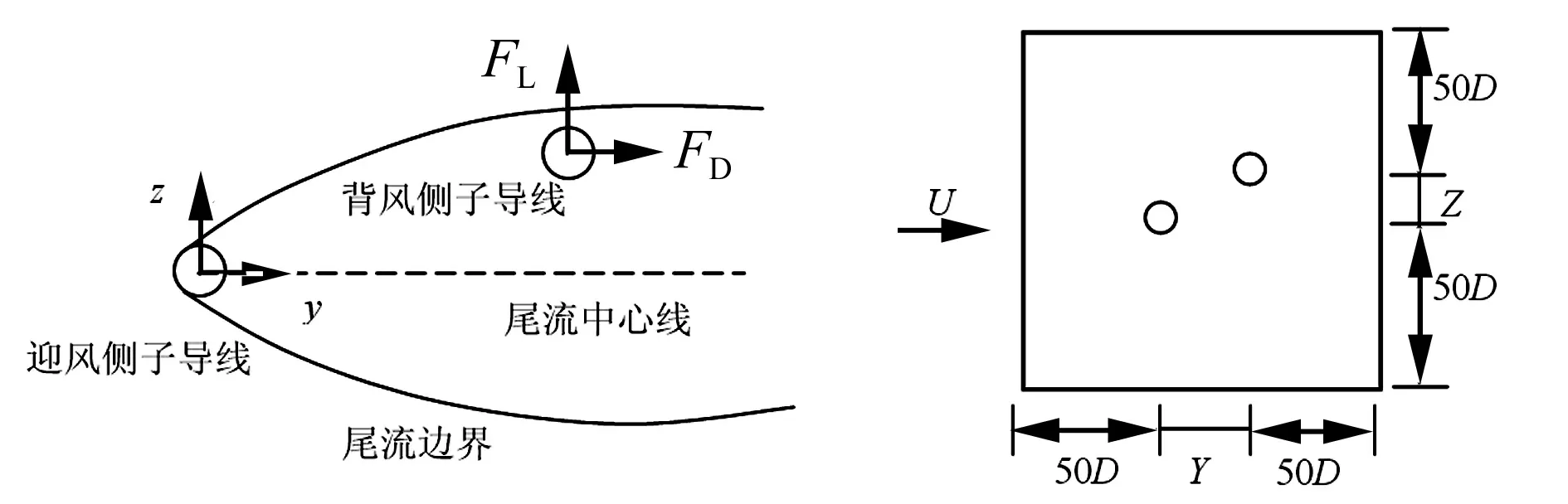
(a) 尾流影响 (b) 计算模型图1 双分裂导线尾流影响及计算模型Fig.1 Wake-induced andsimulation model of twin bundle conductor

在计算得到绕流场后，将导线模型表面的压强进行积分，即可得到作用在导线模型上的升力和阻力。作无量纲化后得到其阻力系数和升力系数

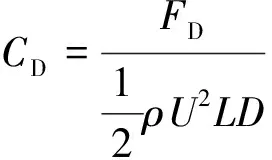
(1)

式中:FD、FL分别为导线模型所受的阻力和升力；ρ为空气密度；U为风速；L为导线模型的有效长度；D为导线的直径。

迎风侧子导线的气动特性基本不受背风侧子导线影响，其类似于单导线。因此，下面重点讨论背风侧子导线的气动特性。如图2所示为双分裂导线水平间距Y为10D，垂直间距Z分别为0D、1.5D和5D时的速度场。可见，两子导线在风作用下均产生了涡脱落现象。当Z=0D时，背风侧子导线受迎风侧子导线尾流干扰严重，但随着垂直距离Z的增大，这种影响逐渐减小，直至消失。

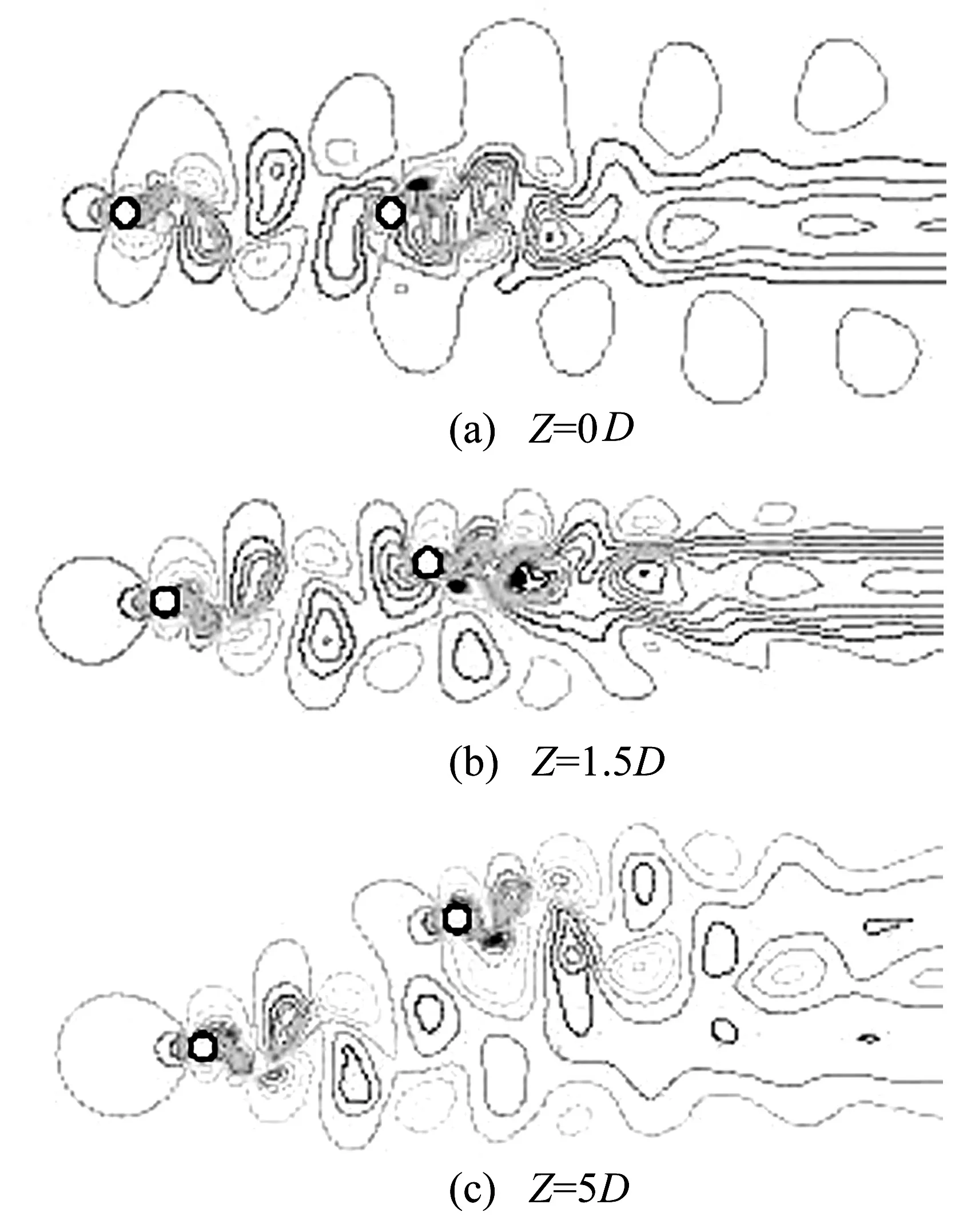
图2 双分裂导线子导线不同间距时的速度场Fig.2 Velocity field of twin bundled conductor with different distance

1.2 子导线气动系数

如图3所示为双分裂导线不同水平间距时，子导线气动系数随垂直间距的变化规律。可见，不同水平间距下，背风侧子导线的阻力系数和升力系数随垂直间距的变化趋势相似。随着水平间距的增大，最小阻力系数增大，而升力系数的最大值随水平间距的增大而减小。

阻力系数曲线关于尾流中心线对称，均为正值，且越靠近尾流中心越小。当垂直间距Z接近4D时其值趋于1.2，即接近单圆柱的阻力系数。而升力系数曲线关于尾流中心线反对称，在尾流中心线上为0，随着垂直间距的增大，升力系数先增大后减少，在尾流边界处接近于0。在尾流中心线以上升力系数为负值，在中心线以下为正，即升力始终指向尾流中心。这些规律与风洞试验结果一致，表明数值模型和结果是合理正确的。

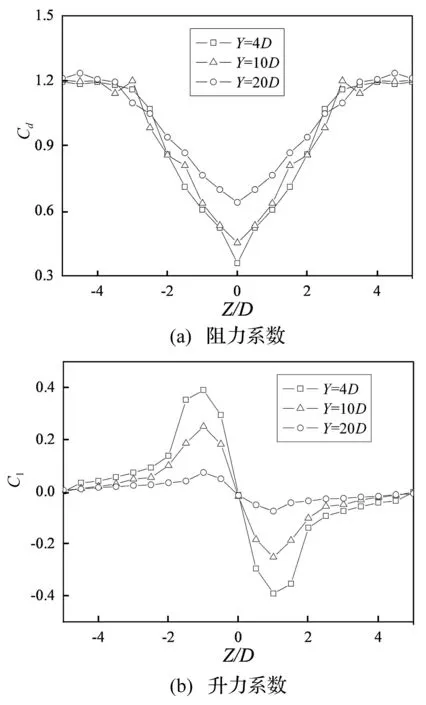
图3 不同水平间距时背风侧子导线气动系数随垂直间距的变化Fig.3 Aerodynamic coefficients of leeward conductor varying with vertical interval in different horizontal interval

图4为背风侧子导线的阻力系数和升力系数在尾流区中的变化规律。从图中可见，水平间距在30D以内，阻力系数的最小值变化较大；在此范围之外，其最小阻力系数随水平位置变化较小；阻力系数在垂直间距接近±4D时趋于最大值1.2。另一方面，子导线升力系数水平间距的影响范围约为20D，垂直间距影响范围约在±3D以内。总之，背风侧子导线的气动特性在迎风侧子导线尾流区内的变化明显，在研究次档距振动时不可忽略。

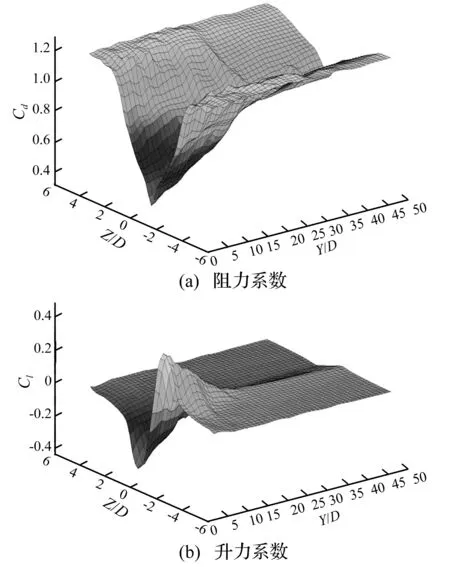
图4 背风侧子导线气动系数在尾流区中的变化规律Fig.4 Aerodynamic coefficients of leeward conductor varying in the wake

2 线路模型及其固有频率和模态

2.1 典型线路段模型

以档距200 m的双分裂线路段为研究对象，导线参数如表1所示。线路的初始水平张力为29.988 kN。线路上安装3个间隔棒，每个间隔棒的质量为4.8 kg，采用非等间距和等间距两种布置方案。非等间距布置方案按现行输电线路设计规程[14]确定，第1个间隔棒距离左端43.33 m，其余依次增加70 m和53.33 m。等间距布置时，各间隔棒之间相距50 m。线路简化模型如图5所示，导线两端固定，风垂直作用于线路。

表1 导线参数

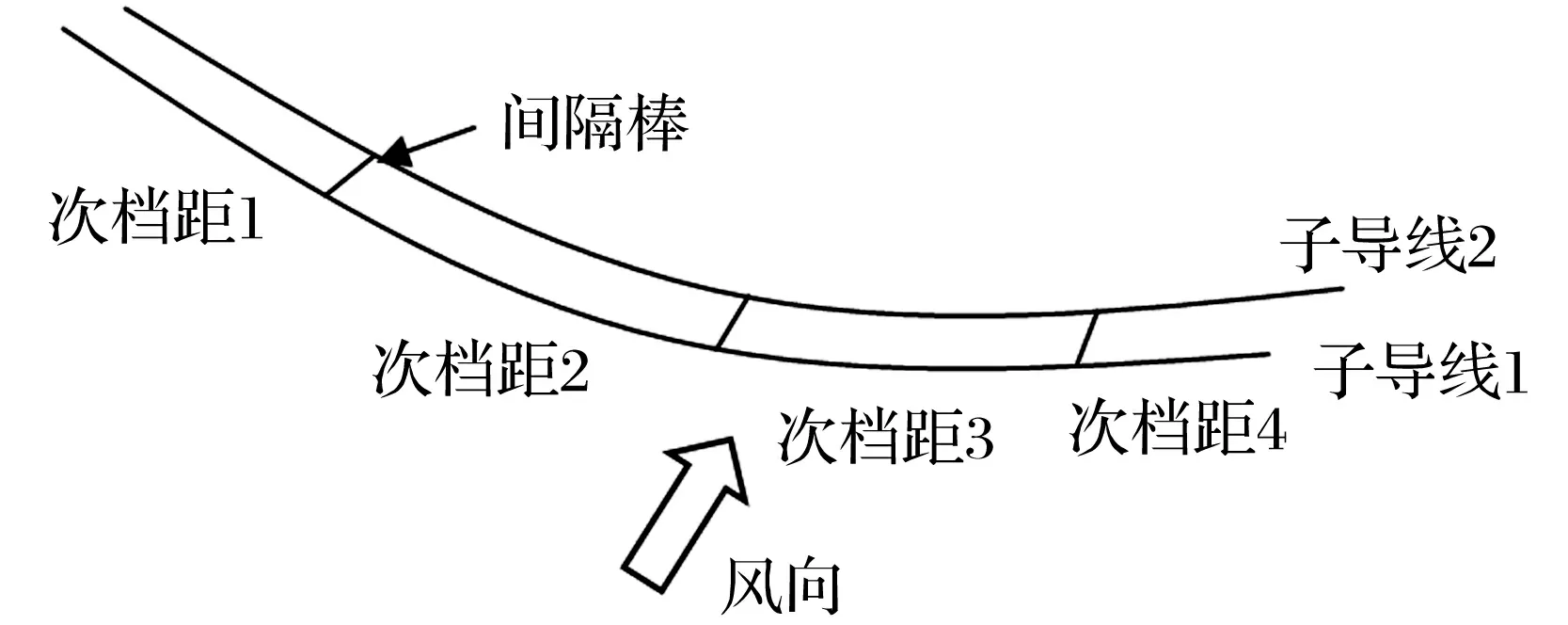
图5 双分裂线路简化模型Fig.5 Simplified model of twin double conductor line

2.2 整档模态和次档距局部模态

尾流诱发振荡发生时，除了发生次档距振动外，还可能发生整档振动。整档振动特征与整档的模态和固有频率有关，而次档距振动与次档距局部模态有关。利用ABAQUS软件分析得到两种间隔棒布置方式下该线路段在面内和面外的低阶模态和固有频率，如表2所示。可见，间隔棒的布置方式对线路整档模态和固有频率的影响非常小。

表2 线路段整档低阶模态和固有频率

Tab.2 Natural frequencies and modes of conductor line

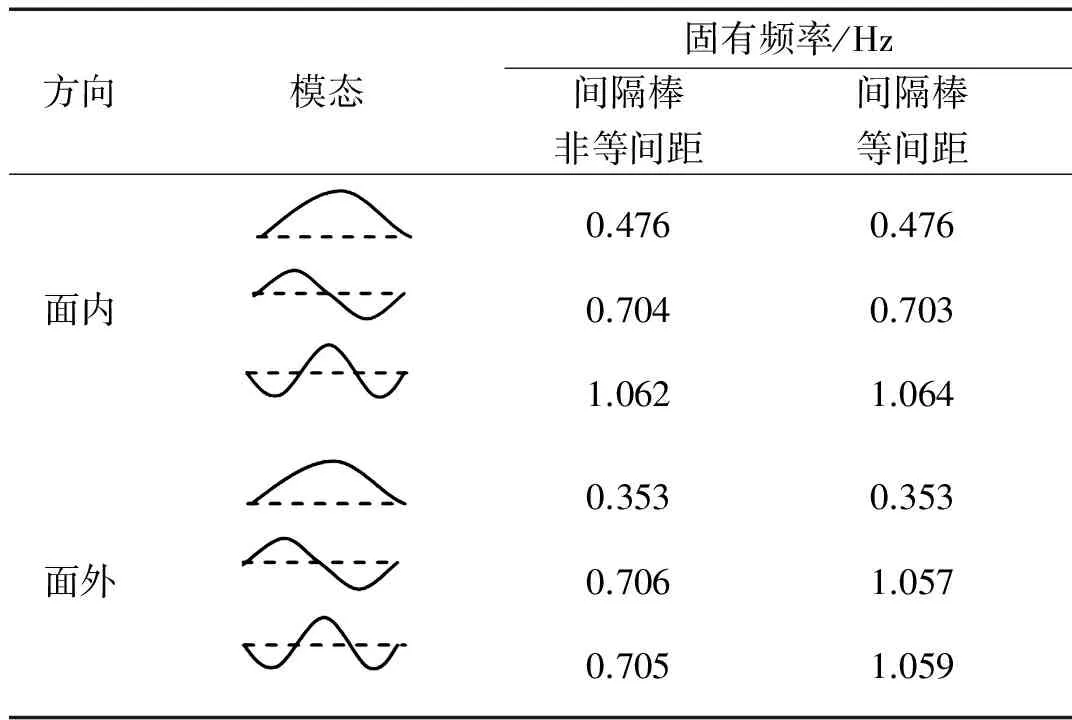
方向模态固有频率/Hz间隔棒非等间距间隔棒等间距面内0．4760．7041．0620．4760．7031．064面外0．3530．7060．7050．3531．0571．059

此外，间隔棒等间距布置时，线路在频率1.418 Hz开始出现密集的次档距局部模态；而间隔棒非等间距布置时，在1.011 Hz便出现次档距局部模态。图6所示为间隔棒两种排布方式的典型次档距局部模态和频率。

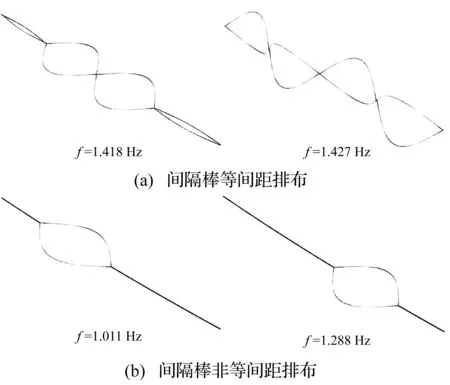
图6 线路段典型次档距局部模态和频率Fig.6 Local sub-span modes and frequencies of twin bundle conductor line

3 尾流诱发振荡数值模拟

3.1 数值模拟方法

输电导线属于柔性结构，其运动过程中的变形属于典型的几何非线性问题。本文采用ABAQUS有限元软件模拟尾流诱发振荡过程。在ABAQUS软件中，可将空间杆单元的材料性质设置为不可压缩得到索单元来模拟导线，而间隔棒采用空间梁单元模拟。在此，导线单元尺寸取0.5 m，经检验，可以满足单元收敛性。

作用在迎风侧子导线上的气动载荷仅有阻力，其阻力系数为1.2。作用在背风侧子导线上的气动载荷与其在尾流区中的位置有关，即与导线的运动状态有关。根据式(1)，作用在子导线上的气动力由式(2)确定

(2)

式中:气动系数CL(y,z)和CD(y,z)与导线运动过程中当前时刻的位置有关，通过其当前位置，可计算出其与迎风侧子导线之间的相对距离，再利用图4中的曲面进行插值确定其值。气动载荷的施加利用ABAQUS用户自定义单元子程序UEL实现[15]。

3.2 间隔棒等间距布置时次档距振动特征

图7为间隔棒等间距布置时，次档距2的两根子导线中点的位移时程曲线及运动轨迹。可以看出，导线的水平振动幅值较大，而垂直振动幅值较小，导线的运动轨迹接近椭圆，且椭圆主轴与尾流中心线的夹角较小。

图8所示为间隔棒等间距布置时各次档距中点子导线一个周期的运动轨迹。从图中可见，子导线1与2的位移相位差接近180°，与现场观察到的现象相一致[16]。此外，次档距1中子导线1的运动沿顺时针方向，子导线2的沿逆时针方向；而次档距3中两子导线的运动均沿逆时针方向，但这两种运动方式中两子导线的位移相位均相反。

图9为间隔棒等间距布置时线路在某时刻的运动状态。可见，此时次档距1中点两子导线呈张开状态，即所谓的“呼”；次档距2呈闭合状态，即所谓的“吸”。同理，次档距3的状态为“呼”，次档距4的状态也为“呼”。这一现象与现场观测结果也是一致的。

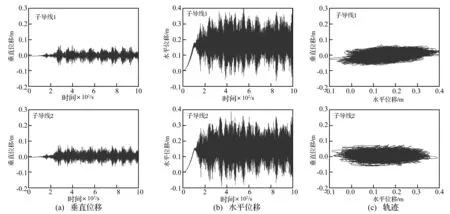
图7 间隔棒等间距布置时次档距2导线中点的位移时程和运动轨迹Fig.7 Time histories of displacements and motion traces at middle of sun-span 2 with equally arranged spacers

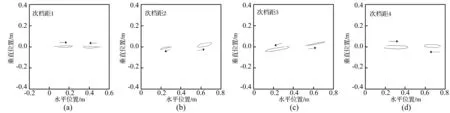
图8 间隔棒等间距布置时各次档距中点子导线的运动轨迹Fig.8 Motion traces of sub-conductors at the middle of sub-span with equally arranged spacers

图9 间隔棒等间距布置时某时刻导线的运动状态(位移放大10倍数)Fig.9 Motions status of conductor lines with equally arranged spacers at typical times (displacement magnification times: ten)

表3为间隔棒等间距布置时各次档距中点子导线的振动幅值的均方根值(Root Mean Square,RMS)。可见，垂直振幅的最小值为0.034 m，最大值为0.082 m；水平振幅的最小值为0.168 m，最大值为0.392 m。虽然间隔棒是等间距排布，但四个次档距的振动幅值并不相等，且两端次档距的振动幅值比中间的要小。

分裂导线发生尾流诱发振荡时，子导线间可能发生“碰线”。图10为各次档距中点两子导线间距的时程曲线。由图可知，各次档距中点两子导线的间距在0.4 m处上下波动。表4给出了各次档距中点两子导线的最大和最小间距，最小距离为0.146 m，最大距离为0.606 m，发生在次档距2的中点。可知子导线并未发生碰线。

表3 间隔棒等间距排布时各次档距中点两子导线的振动幅值

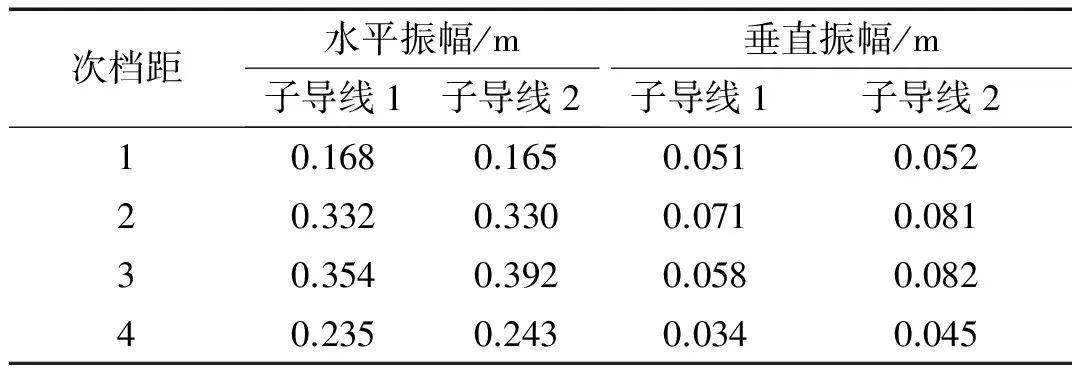
Tab.3 Oscillation amplitudes of conductors at the middle of sub-spans with equally arranged spacers

图10 间隔棒等间距排布时各次档距中点两子导线的间距随时间的变化Fig.10 Space between two sub-conductors at the middle of sub-spans varying with time with equally arranged spacers

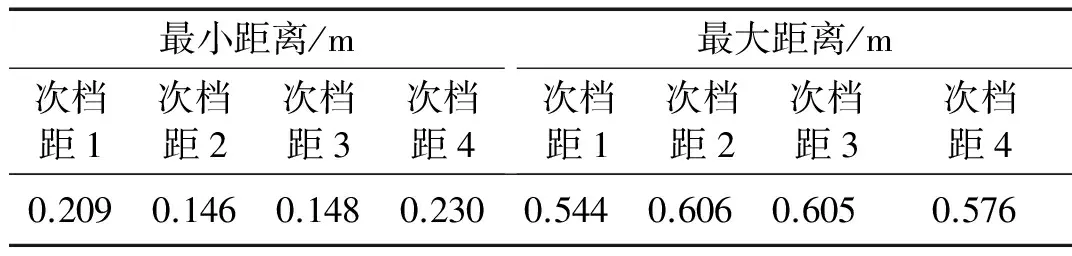
Tab.4 The maximum and minimum distance of two sub-conductors at the middle of sub-spans varying with time with equally arranged spacers

图11所示为次档距1两子导线中点位移的频谱。由图11(a)可见， 水平位移的频谱在0.353 Hz、0.700

Hz和1.390 Hz处出现峰值。由表2中结果可知，第一和第二个峰值分别接近于整档面外单半波和双半波振动模态的固有频率，即整档运动包含了单半波和双半波模态响应。参见图6可知，第三个频率峰值与次档距局部固有频率1.418 Hz相接近，即线路发生了次档距振动。

此外，由图11(b)可知，垂直位移的频谱在接近于面内单半波和双半波模态对应的固有频率附近出现峰值，而对应于次档距固有模态的频率峰值很小，说明发生次档距振动主要为面外振动。

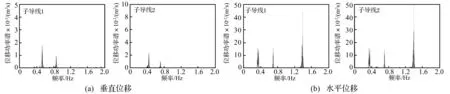
图11 间隔棒等间距时次档距1中点的位移频谱Fig.11 Displacement spectra of sub-conductors at the middle of sub-span1 with equally arranged spacers

3.3 间隔棒非等间距布置时次档距振动特征

本节讨论间隔棒按现行输电线路设计规程确定的排布方式下，其尾流诱发振荡的特征。图12为各次档距中点子导线一个周期的运动轨迹。可见，子导线1和子导线2的位移相位差接近180°，与间隔棒等间距布置时相一致。表5为各次档距中点子导线振动幅值，子导线水平振幅仍远大于垂直振幅。从间隔棒排布方式来看，次档距2的长度为70 m，是四个次档距中最大的，其振动幅值也最大；而次档距4的长度为33.33 m，长度最小，其振动幅值也最小。因此，次档距的长度对子导线振动幅值有较大影响。比较表3和表5中的结果可以看出，间隔棒两种排布方式的垂直振幅相差不大，但等间距排布时的水平振幅远大于非等间距排布的振幅。因此，采用非等间距排布方式可以大大减小尾流诱发振荡的振动幅值。

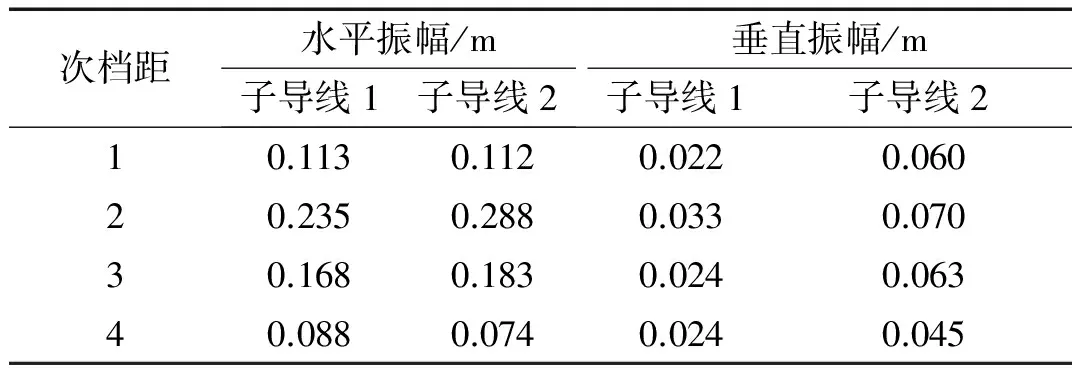
次档距水平振幅/m子导线1子导线2垂直振幅/m子导线1子导线210．1130．1120．0220．06020．2350．2880．0330．07030．1680．1830．0240．06340．0880．0740．0240．045

表6为各次档距中点两子导线的最大和最小距离。其中，最小距离为0.213 m，最大为0.502 m，子导线未发生碰线。间隔棒非等间距排布时次档距中点距离变化范围小于等间距排布。

表6 间隔棒非等间距排布时各次档距中点子导线间的距离

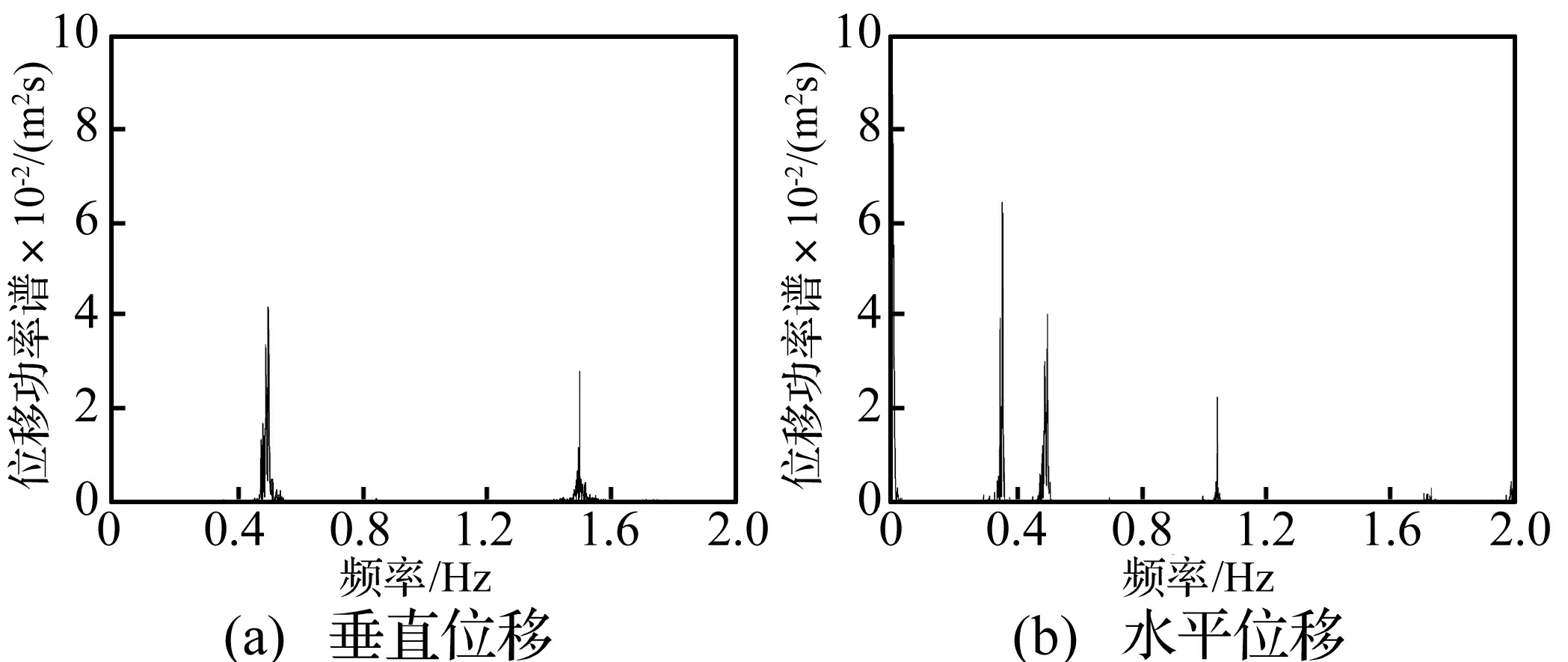
图13 间隔棒非等间距排布时次档距4中点子导线2的位移频谱Fig.13 Displacement spectra of sub-conductor 2 at the middle of sub-span 4 with equally arranged spacers

图13为次档距4子导线2中点位移的频谱。水平位移的频谱在0.356 Hz、0.499 Hz、1.044 Hz处出现峰值，第一个和第二个峰值分别对应水平单半波和垂直单半波振动模态频率，即，此时线路整档振动的主模态为单半波。第三个峰值对应于次档距模态频率1.011 Hz。

4 结 论

本文利用Fluent流体动力学软件模拟得到双分裂导线的气动系数，并利用ABAQUS软件模拟双分裂导线的尾流诱发振荡，得到如下结论：

(1)背风侧子导线的气动特性受其与迎风侧子导线间距的影响明显，研究分裂导线尾流诱发振荡时不可忽略。

(2)数值模拟结果表明，尾流诱发振荡过程中，导线的运动轨迹近似为水平椭圆，两子导线的位移相位差反相，接近180°，且水平振动幅值比垂直振动幅值大，与现场观察结果一致。

(3)间隔棒非等间距排布时导线的次档距振动幅值明显小于等间距排布情况。

(4)本文结果对双分裂导线次档距振荡的抑制方法和技术研究具有重要的参考价值，其方法可以进一步用于研究不同线路的间隔棒布置方案的优化。

[ 1 ] SNEGOVSKIY D. Wake-induced oscillations in cable structures: finite element approach [D]. Moscow: University of Liege , 2010.

[ 2 ] PRICE S J. Wake induced flutter of power transmission conductors [J]. Journal of Sound and Vibration, 1975, 38(1):125-147.

[ 3 ] DIANA G, BELLOLI M. Wind tunnel tests on two cylinders to measure subspan oscillation aerodynamic forces[J]. IEEE Transactions on Power Delivery,2014, 29(3):1273-1283.

[ 4 ] 陈元坤. 分裂导线的微风振动与次档距振动研究[D]. 武汉:华中科技大学,2011.

[ 5 ] WARDLAW R L, COOPER K R, KO R G, et al. Wind tunnel and analytical investigation into the aeroelastic behavior of bundled conductors [J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(2):642-651.

[ 6 ] TSUI Y T. On wake-induced vibration of a conductor in the wake of another via a 3D finite element method[J]. Journal of Sound and Vibration, 1986, 107(1):39-58.

[ 7 ] HARDY C, VAN DYKE P. Field observations on wind-induced conductor motions [J]. Journal of Fluids and Structures, 1995, 9(1):43-60.

[ 8 ] YANG J W, YU Z M, LUO S Q, et al. Optimization design on subspan oscillation of multi-conductor[J]. Advanced Materials Research, 2014, 940:347-350.

[ 9 ] 李黎，王腾飞，陈元坤. 分裂导线次档距振荡研究[J]. 振动与冲击，2014,33(17)：62-67. LI Li, WANG Tengfei, CHEN Yuankun. Research of sub-span oscillation of split conductor [J]. Journal of Vibration and Shock, 2014,33(17)：62-67.

[10] 严波，蔡萌琦，吕欣,等. 四分裂导线尾流驰振数值模拟研究[J]. 振动与冲击，2015，34(1)：182-189. YAN Bo, CAI Mengqi, LÜ Xin, et al. Numerical simulation on wake galloping of quad bundle conductor [J]. Journal of Vibration and Shock, 2015,34(1)：182-189.

[11] BELLOLI M, MELZI S, NEGRINI S, et al. Numerical analysis of the dynamic response of a 5-conductor expanded bundle subjected to turbulent wind [J]. IEEE Transactions on Power Delivery, 2010, 25(4):3105-3112.

[12] RAWLINS C B. Fundamental concepts in the analysis of wake-induced oscillation of bundled conductors [J]. IEEE Transactions on Power Apparatus and Systems, 1976,95(4):1377-1393.

[13] CAI M Q, YAN B, LÜ X, et al. Numerical simulation of aerodynamic coefficients of iced quad bundle conductors [J]. IEEE Transactions on Power Delivery, 2015, 30(4):1669-1676.

[14] 张殿生.电力工程高压送电线路设计手册[M]. 北京：中国电力出版社,2003.

[15] HU J, YAN B, ZHOU S, et al. Numerical investigation on galloping of iced quad bundle conductors [J]. IEEE Transactions on Power Delivery，2012，27(2)：784-792.

[16] SOHN H K, LEE H K, CHU J H, et al. Field observation and analysis of wind-induced vibrations in four-bundled conductor transmission lines [J]. KIEE International Transactions on PE, 2003, 3(2):109-114.

A numerical simulation on wake-induced oscillation of twin bundle conductor lines

HEXiaobao1,YANBo1,2,WUChuan1,ZHANGBo3,4,YANGXiaohui3,4

(1. College of Aerospace Engineering, Chongqing University, Chongqing 400044, China; 2. State Key Laboratory of Transmission & Distribution Equipment and Power System Safety and New Technology, Chongqing University, Chongqing 400044, China; 3. Henan Electric Power Research Institute, Zhengzhou 450052，China; 4. Key Laboratory of Galloping Simulation Technology of Transmission Line, State Grid Corporation , Zhengzhou 450052, China)

Lift coefficient and drag coefficient of leeward conductors varying with relative position of upwind conductors were simulated by fluid dynamics software Fluent. The wake-induced oscillation of typical twin bundle conductor lines were numerically simulated by ABAQUS software. The moving traces, vibration amplitude and frequency characteristics of sub-conductors were obtained. It is shown that the displacement phases of the two sub-conductors are opposite, and the moving traces are approximated as a horizontal ellipse. The simulation results are consistent with the field observation results. Finally, the characteristics of wake-induced oscillation of the twin bundle conductor line with equally and unequally installed spacers are compared.

twin bundle conductor; aerodynamic coefficient; wake-induced oscillation; numerical simulation

国家自然科学基金(51277186)；国家电网公司科技项目(521702140013)

2015-11-09 修改稿收到日期：2016-01-20

何小宝 女，硕士生，1990年9月生

严波 男，博士，教授，1965年5月生 E-mail: boyan@cqu.edu.cn

TM753;O39

A

10.13465/j.cnki.jvs.2017.04.010