基于灰色预测模型的青岛市卫生技术人员需求预测分析

王红霞，李志荣，薛刚，侯亚娟

青岛市卫生计生发展研究中心，山东青岛266000

基于灰色预测模型的青岛市卫生技术人员需求预测分析

王红霞，李志荣，薛刚，侯亚娟

青岛市卫生计生发展研究中心，山东青岛266000

卫生人员预测在卫生事业管理中占有重要地位，是卫生人力资源配置的重要依据。应用灰色预测GM(1,1)模型，以2005—2014年青岛市卫生技术人员数据资料为依据，求解模型得到青岛市2015—2020年卫生技术人员预测值，将实际值与预测值进行对比分析，检验结果表明模型预测结果较好，精度较高，误差率小。用该模型得到2015—2020年青岛市卫生人员预测值，为青岛市卫生人力资源规划提供依据。

GM(1,1)模型；灰色预测；青岛市；卫生技术人员

人力资源是卫生事业的战略性资源，卫生部门和机构的其他资源都是人力资源的附属资源。科学与合理的卫生人力资源配置会给居民带来更好的健康状况，同样还会改善整个卫生系统的绩效。因此，如何有效地配置卫生人力资源是区域卫生规划的重要问题[1]。目前，灰色预测模型被越来越多的专家认可和推荐，已成为人力预测方法中最有发展前途的方法之一[2-3]。该研究通过搜集青岛市2005—2014年卫生技术人员数资料，运用GM (1,1)模型灰色预测法对其进行分析和预测，为青岛市卫生人力资源培养与配置提供决策依据。

1 灰色预测模型

目前应用最为广泛的灰色预测模型就是关于数列预测的一个变量、一阶微分的GM(1,1)模型。GM(1,1)模型是基于随机的原始时间序列,经按时间累加后所形成的新的时间序列呈现的规律可用一阶线性微分方程的解来逼近。经证明，一阶线性微分方程的解逼近所揭示的原始时间数列呈指数变化规律,因此,当原始时间序列隐含着指数变化规律时,灰色模型GM(1,1)的预测将是非常成功的。

2 GM(1,1)模型原理

灰色预测GM（1,1）模型是一个拟微分方程的动态系统，其建模的实质是对原始数据先进行一次累加生成，使生成的数据序列呈现一定规律，而后通过建立一阶微分方程模型，求得拟合曲线，用以对系统进行预测。具体过程如下。

①给定原始序列：

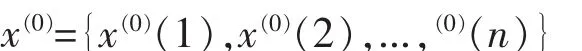
②1-AGO生成序列：

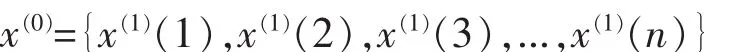
③紧邻均值生成序列：

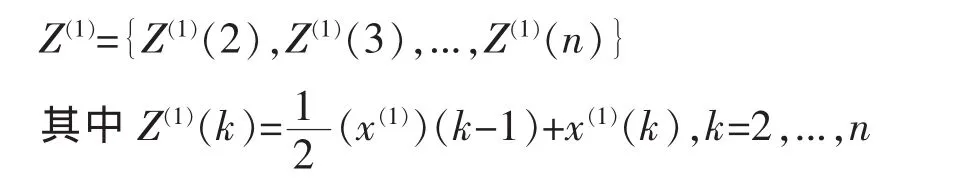
④建立灰色微分方程：

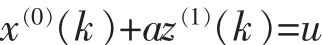
⑤对应的白化方程为：

⑥解得离散化形式为：

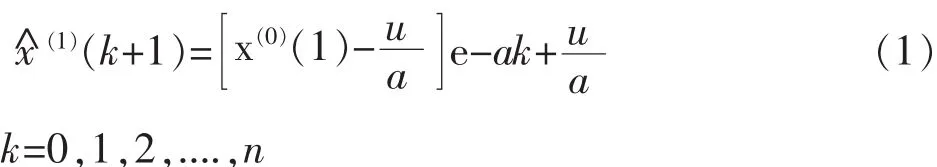
⑦1-AGO还原序列：

3 应用实例分析

利用2005—2014年青岛市卫生技术人员数据资料(数据来源于2015年青岛市统计年鉴)，应用灰色系统理论构建GM（1，1）预测模型，预测青岛市2015—2020年卫生技术人员规模。

3.1 建立预测模型

通过上述公式计算（见第2部分GM(1,1)模型原理），得出a=-0.0875，u=27115.3149代入公式（1），得预测模型为：

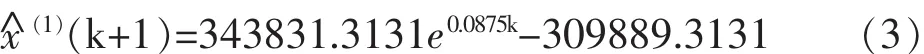
将k=0,1,2,…,9代入（3），得2005—2014年累加值。由公式（2）求出预测值，求出预测值，结果见表1。

3.2 模型精度检验

（1）残差检验。

绝对残差序列：

相对残差序列：

利用公式（4）求出绝对残差，利用公式（5）求出相对残差，结果见表1。利用公式（6）求出平均误差为2.25%。

表1 青岛市卫生技术人员数预测值与实际值的相对误差

从灰色预测方法原理可知，-a主要控制系统发展态势的大小，即反映预测的发展态势，被称为发展系数；u的大小反映了数据变化的关系，被称为灰色作用量，其中：①当-a＜0.3时，GM(1,1)模型可用于中长期预测；②当0.3＜-a＜0.5时,GM(1,1)模型可用于短期预测，中长期预测慎用；③当0.5＜-a＜1时,应采用GM(1,1)改进模型，包括GM(1,1)残差修正模型；④当-a＞1时,不宜采用GM(1,1)模型,可考虑其他预测方法。

表2 精度检验等级参照表

（2）关联度检验。

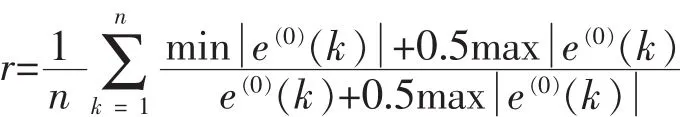
该例中

满足ρ=0.5时，r＞0.6的检验标准。

（3）后检查检验。

由原始数据序列x（0）（t）和绝对误差序列Δ（t）计算得原始数据序列和绝对误差序列的标准差分别为:

由原始数据序列x（0）（k）和绝对误差序列e（0）（k）计算得原始数据序列和绝对残差序列的标准差分别为：

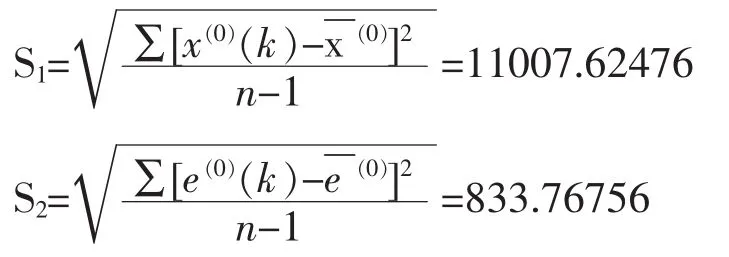
设S=0.6745 S1，则S=7424.6429，由于所有M均小于S，所以P=1。

表3 灰色预测精度检验等级标准

将检验指标P和C与灰色预测精度检验等级标准见表3，对比可知，预测模型较好。将k=9,10,11,12,13,14代入公式（3），经计算得到2015—2020年卫生技术人员数，见表4。

R197.1

A

1672-5654（2017）01（c）-0003-03

10.16659/j.cnki.1672-5654.2017.03.003

王红霞（1983.7-），女，山东临邑人，硕士，助理工程师，研究方向：卫生统计、卫生政策研究。