基于水平集方法和最小距离函数法的复杂装药燃面退移问题研究

王革， 韩万之， 李冬冬， 郜冶

(哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001)

基于水平集方法和最小距离函数法的复杂装药燃面退移问题研究

王革， 韩万之， 李冬冬， 郜冶

(哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001)

利用水平集(Level-set)方法和最小距离函数(MDF)方法，对固体火箭发动机装药燃面退移问题进行研究。基于Level-set方法和MDF方法的相互耦合，建立了一种可以准确预测固体推进剂装药燃烧表面退移的方法；对不同几何药型、不同燃速组合推进剂装药及带侵蚀效应的装药进行计算分析，其结果表明，该组合方法及所采用的网格界面分割和几何重构计算燃面面积的思想，在预测固体推进剂装药燃面瞬态退移问题上具有良好的适应性和较高的可信度。

兵器科学与技术； 装药燃面退移； 燃面面积； 水平集方法； 最小距离函数方法

0 引言

准确的固体火箭发动机内弹道计算对于预测固体火箭发动机工作过程有着重要意义，而装药燃面退移过程直接决定着其内弹道变化特性。

目前国内外燃面退移实现方法主要有以下5种：

1)通用坐标法。该方法于1968年，由Peterso等[1]提出，主要思想是：将初始空腔分解为基本几何元素，通过几何元素的扩大，实现燃烧表面退移。1975年，Nickson等[2]将通用坐标法应用到内弹道计算中，设计开发了固体火箭发动机性能程序(SPP)，经过后来一系列改进，成为了固体火箭发动机性能评估的标准。侯晓等[3]和周华盛[4]通过对通用坐标法计算燃面结果跳动的分析，分别采用直接求解燃面和通过将肉厚等份数设置为积分区间长度的倍数减小体积分误差的方法，消除了计算结果的波动。鲍福廷等[5]在通用坐标法的基础上，结合计算机图形处理直接获得几何数据，研制了三维装药设计程序，并建立了一套图形库。这种处理方式不依赖于复杂的求交运算，可以获得更为完备的燃烧室内通道参数，为一维内弹道计算及内流场计算提供详尽的数据。

2)实体造型法。随着几何造型技术的发展，出现了很多依托计算机辅助设计CAD软件平台，进行二次开发的方法，可以得到任意时刻燃面和与药柱体积相关的信息。1993年，田维平等[6]借助计算机辅助设计与辅助制造I-DEAS软件和实体造型方法设计开发了药柱CAD燃烧模拟分析系统——CAPBAS. 1993年，方蜀州等[7]利用实体造型法思想，借助AutoCAD11.0的绘图功能，在其高级造型扩展软件包AME的基础上开发了用于燃面计算的Regress3D程序。2003年，颜仙荣等[8]以计算机辅助设计与辅助制造UG软件为开发平台借助UG的实体造型功能，完成了固体火箭发动机装药的设计、燃面退移模拟和燃面计算，与实验结果的对比表明该方法具有较高的精度。2014年，刘伟[9]借助建模软件Pro/E，使用Qt平台进行软件界面的开发，实现了发动机药型设计与内弹道计算，并且可与通用计算流体力学CFD软件进行数据交流，实现药型设计、内弹道计算与流场计算一体化。

3)动网格方法。1995年，Hejl等[10]，用自适应网格方法解决轴对称和二维装药燃面计算问题，实现了不等速燃烧燃面计算。1998年，Breton等[11]用非结构网格方法进行二维装药内弹道计算，通过求解汉密尔顿一雅克比方程，解决不等速燃烧燃面计算问题。2014年，Gueyffier等[12]使用水平集(Level-set)方法和傅里叶变换等多种复杂运算及高阶算法计算界面节点移动，并配合使用体网格适应技术避免网格的重新划分。用来计算复杂药型的内流场，得到了比较好的结果。2005年，沈伟等[13]根据惠更斯波传播原理，构建了一种在CFD软件非结构网格系统上直接计算燃面推进的数值方法并实现了燃面推进。2006年，Jiao[14]提出了一种新的面网格移动技术——face offsetting。该技术提供了一个动网格界面移动的统一框架，即使燃面存在奇点和大曲率半径也可以得到比较精准的结果。2008年，贺征等[15]使用动态层方法对星形装药燃面退移及内流场进行了一体化计算，计算结果和准稳态计算结果以及实验数据的对比表明，动网格方法可以得到优于准稳态的结果。2013年，LI等[16]使用了face offsetting方法进行药柱燃面退移计算，配合网格光顺和网格重构技术处理流体域网格变形和扭曲，模拟了三维复杂药柱燃面退移内流场，结果和实验吻合较好。

4)界面追踪法。界面追踪法将发动机燃面视为流场中的自由边界，通过一定手段追踪或者捕获燃面位置，然后求得有关燃面面积和装药体积。其中用的最多的是Level-set方法。1996年，Sethian等[17]利用LSM，建立运动界面的控制方程，通过求解实现了对自由界面的追踪。2001年，HEGAB等[18]发展了一种异质推进剂的非稳态燃烧模型，同时模拟气相的燃烧和固相的传热，并且在界面处施加阶跃。在模拟界面退移时使用了Level-set方程推导出的汉密尔顿-雅克比方程，并且通过Level的不同标识出高氯酸铵(AP)和黏结剂。2003年，秦飞[19]将Level-set方法用于燃面计算。将装药燃面看作不同物质的分界面，建立了燃面控制方程，通过求解控制方程计算出燃面变化规律，并对含缺陷装药和变燃速装药进行了计算。2005年，Yild等[20]用LSM分别对二维和三维装药下不等燃速燃烧情况进行计算。2011年，Cavallini等[21]用准一维非稳态内弹道耦合Level-set界面退移计算了发动机从开始点火到推进剂燃烧殆尽整个过程，该方法特别适合计算侵蚀燃烧下发动机的内弹道，且可以给出比零维内弹道更准确的压力变化曲线。2014年，Wang等[22]使用Level-set方法和零维内弹道耦合计算发动机燃面退移，并将其应用于固体火箭发动机的装药设计。2014年，Hwang等[23]发展了3种使用固定网格的界面追踪法：界面追踪、射线法和最小距离函数(MDF)法。界面追踪是基于拉格朗日视角的方法，而射线法和MDF法是基于欧拉视角的方法。使用这3种方法进行模拟，发现MDF法比其他两种方法要更准确。2015年，何涛等[24]以FLUENT为平台，利用UDF进行二次开发，完成了星型装药燃面点火和燃面退移的建模， 研究了星型装药固体火箭发动机点火和燃面退移过程。

5)MDF方法。2005年，Willcox等[25]提出了MDF燃面计算方法，处理燃面计算普遍存在的通用性和稳定性问题。2007年，马长礼[26]对MDF迭代过程进行改进，提高了MDF方法燃面计算的精度，通过大量算例验证了MDF方法的通用性，对不等燃速燃面计算也进行了尝试。2009年，熊文波等[27]在单元法中，使用了网格到燃面的最小距离判断某一时刻单元内装药是否燃尽，通过相邻肉厚的体积微分获得燃面面积。这种方法避免了大量的数学推导，也避免了内型面标准几何体的复杂定义。

国内外研究工作表明，界面追踪方法已经比较好地运用到固体火箭发动机装药的燃面退移计算中，其中Level-set方法得到了比较好的结果。但是Level-set使用和计算也存在着一些问题，通常使用的都是汉密尔顿- 雅克比形式的Level-set方程，而这种方法在退移界面的曲率过大或过小时，求解存在问题，计算存在凸尖点的界面退移时需要特殊处理。本文主要结合MDF燃面计算方法，对Level-set方法进行改进，使其在燃面退移的计算上更加方便和准确，发展精确的燃面面积计算方法，为燃面退移和流场的耦合计算提供良好的基础。

1 数值方法与计算方案

1.1 计算方法

采用Level-set方法和MDF方法组合技术计算燃面退移。Level-set方法求解需要初场和燃面(界面)退移速度场，求解后可以得到当前燃面位置和流体与固体(简称流固)区域划分；MDF方法初始化需要燃面位置和流固区域划分信息，变换后可以为Level-set方程的求解提供所需的初场和燃面退移速度场，这两种方法可以互相配合，其整个过程如图1所示。

图1 燃面退移计算方案Fig.1 Calculation scheme of burning surface regression

主要流程如下：

步骤1 根据计算域中燃面位置和区域划分(流体区域和固体区域)初始化带符号最小距离函数Φe；

步骤2 变换Φe得到Level-set方程求解所需的水平集函数初场φt和界面退移速度场Vφ；

步骤3 求解Level-set方程，得到t+Δt时刻的水平集函数场φt+Δt；

步骤4 使用t+Δt时刻水平集函数场φt+Δt中的零等值面对计算域中的所有网格进行网格分割和几何重构，得到燃面位置信息，计算燃面面积和固体体积分数；

步骤5 根据t+Δt时刻的水平集函数场φt+Δt确定计算域中流体区域和固体区域的划分；

步骤6 重复步骤1～步骤5，直到计算结束。

1.2Level-set方法

使用Level-set方法求解燃面退移问题，主要就是利用一个水平集函数φ来表征出界面在不同时刻的位置，通常这样的函数φ需要满足两个条件：1)能够表征出流体区域和固体区域；2)能够表征出不同时刻界面的位置。

在此使用φ>0部分表征固体区域，φ<0部分表征外部流体区域，φ=0表征界面，如图2所示。

图2 Level-set水平集函数示意图Fig.2 Schematic diagram of Level-set function

传统level-set方程形式为

(1)

(1)式为非守恒形式，将其转换为守恒形式

(2)

(2)式为由非稳态项、对流项和源项组成的标量方程。

1.3MDF方法

MDF方法基本思想是：计算药柱内部各点到初始燃面的位置，即最小距离函数Φe，按照平行层退移规律，选取Φe的值等于已燃厚度e的点，即可组成已燃厚度e时的燃面，如图3所示，Φe=0是初始燃面位置，Φe=Δe是燃层厚度为Δe时的燃面位置。

图3 MDF方法示意图Fig.3 Schematic diagram of MDF

将MDF在整个计算域上按照如下方式扩展得到带符号的最小距离函：

(3)

式中：d为计算域中某点与初始燃面的距离。

可以说最小距离法可以独立地完成按照平行层退移规律的燃面计算，而且经过其他学者证明，精度和稳定性都很高。当装药燃速大小在空间存在差异时，MDF方法难以用来计算燃面退移，但是可以在燃面附近为燃面提供一个合理的界面退移方向，即MDF的法向。

1.4 界面分割和几何重构

t时刻的水平集函数场φt经过Level-set方程的求解，得到t+Δt时刻的水平集函数场φt+Δt. 根据φt+Δt中的零等值线，即界面，对计算域进行分割，在此使用基于等值面的方法进行界面分割，这种方法可以使界面在网格交界面处连续。为了方便计算界面，在网格内简化为一线段(二维)或平面(三维)，以二维为例，如图4所示。

图4 基于等值线方法的界面分割示意图Fig.4 Interface segmentation based on contour

界面分割之后，需要对重构的网格进行几何运算，求解网格中的界面面积和固体体积分数，以二维四边形网格为例，如图5所示，流程如下：

1)使用泰勒展开求得网格顶点处的水平集函数φ，如图5(a)中的网格顶点A、B、C和D的水平集函数φA、φB、φC和φD；

2)使用零等值线分割网格，如图5(b)中零等值线交网格界面于点E和点F，其中EF即为网格内的界面面积；

3)进行几何重构，排除φ<0的流体区域，剩余固体区域，如图5(c)中剩余多边形ABEFD；

4)对多边形ABEFD的顶点进行顺时针或者逆时针排序，如图5(d)中得到顶点序列P1、P2、P3、P4和P5；

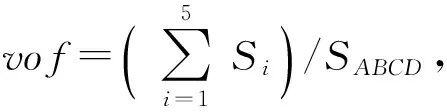
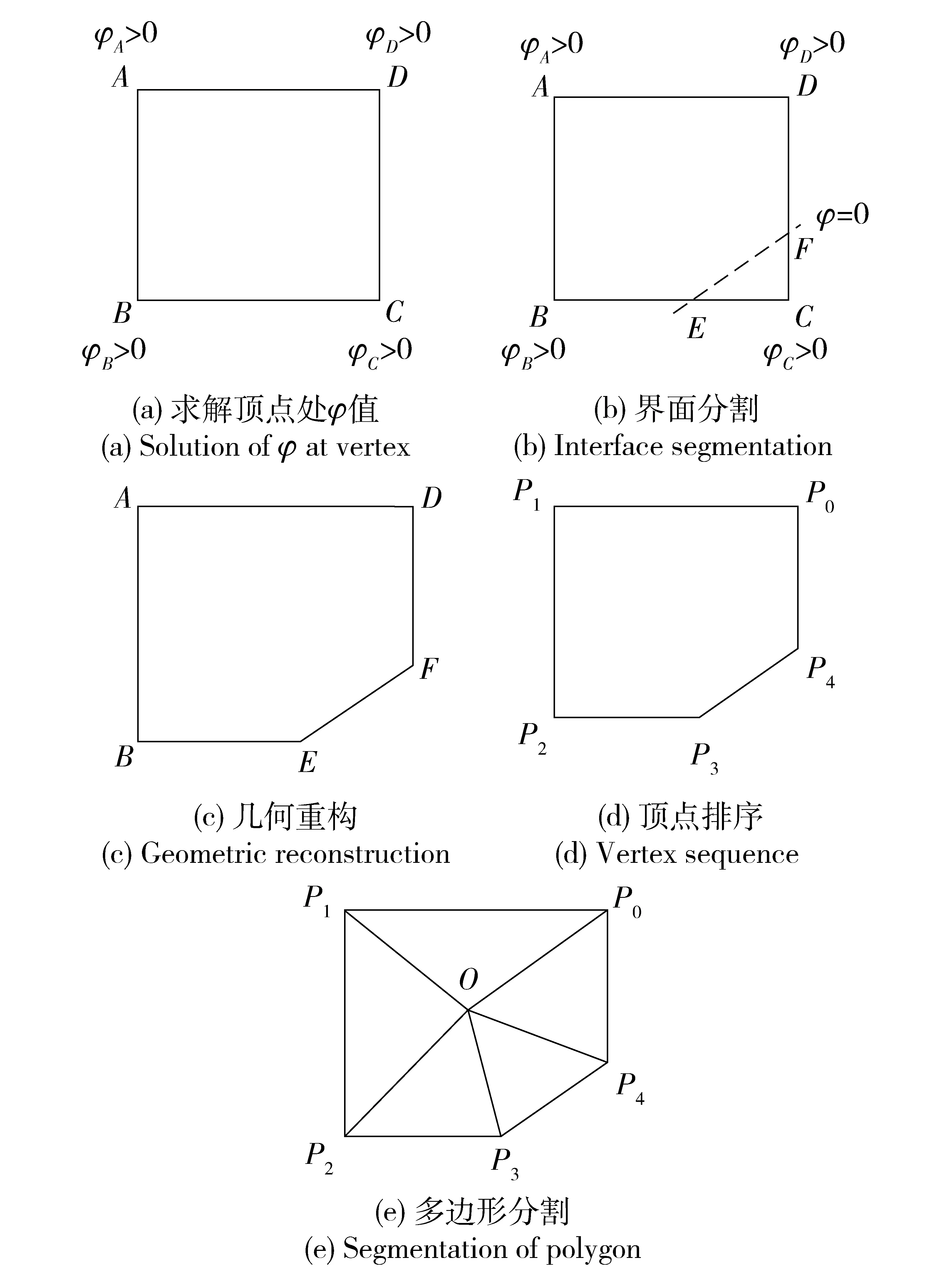
图5 三角分割求解界面面积和体积分数Fig.5 Triangular segmentation for solving interface area and volume fraction

这种网格界面分割和几何重构的方法，适合各种二维凸多边形网格或者三维凸多面体网格，适用性好，方便编程处理；另外，对网格进行界面分割时，可以将重构后得到的退移界面上的节点存储起来，为带符号的距离函数重新初始化提供所需的界面信息。

1.5Level-set方程求解

Level-set方程的求解需要为其指定初场φt和界面退移速度场Vφ.

1.5.1 Level-set初场设置

对带符号的距离函数进行如下变换可以得到一个水平集函数φ，如图6所示。

(4)

图6 水平集函数φ示意图Fig.6 Level-set function

式中：L表示燃面附近的一条窄带的宽度，通常选取网格平均尺寸的4～5倍距离。

选取这样的水平集函数主要有以下优点：

1)能够简单的标识出流体区域、药柱区域及燃面，φ<0的区域为流体区域，φ>0的区域为药柱区域，φ=0的等值面为燃面；

2)在界面附近有1阶线性分布的水平集函数，方便确定界面的准确位置；

3)在远离界面的位置处φ值方便确定，在药柱区域内φ=1.0，在流体区域内φ=-1.0，便于给定边界值，或可以直接使用源项固定部分区域的值作为内边界。

1.5.2 Level-set速度场Vφ的确定

图7 界面退移示意图Fig.7 Interface regression

2 界面退移计算验证

2.1 装药燃面退移分析

推进剂药柱根据燃烧表面的位置可以分为：端面燃烧药柱、侧面燃烧药柱和侧端面同时燃烧药柱。侧面燃烧药柱可分为：外燃药柱、内燃药柱和内外燃药柱。不管药柱如何复杂，根据平行层燃烧规律，再考虑其他因素的影响，燃面退移主要包含以下6种方式，如图8所示。

1)燃面平面退移，如端面燃烧药柱，在退移过程中，燃面始终保持为一平面，如图8(a)所示；

2)燃面凸面退移，如星形药柱的和车轮形药柱等，都存在装药部分凸向燃烧的燃面，在退移过程中，界面当地曲率不断增大，最后出现凸尖点，甚至其后退移过程一直存在凸尖点，如图8(b)和图8(c)所示；

3)燃面凹面退移，如星形药柱和车轮形药柱等存在内燃面的药柱都存在凹向燃烧室的燃面，且初始当地曲率都比较大(极限情况为凹尖点)，在退移过程中，当地曲率不断减小，形成曲率比较小的曲面，如图8(d)和图8(e)所示；

4)燃面部分烧完，燃面到达包覆层等位置，燃面与包覆层相交，如图8(f)所示；

5)装药可能是由不同燃速推进剂组成的，燃面以不同燃烧速度退移，如图8(g)所示；

6)装药部分燃烧表面出现侵蚀燃烧，下游燃速比上游高，如图8(h)所示。

图8 装药燃面退移示意图Fig.8 Schematic diagram of grain burning regression

为了验证Level-set方法和MDF方法组合技术是否能够用来计算上述燃面退移，采用以下4种计算模型进行验证：

1)三维星形装药，星形装药燃面在退移过程中，退移形式包含了图8(a)～图8(f)的6种形式；

2) 复杂三维装药燃面退移，退移形式包含了图8(a)～图8(f)的6种形式；

3) 不同燃速推进剂组成的单管内外燃装药燃面退移，可以用来检验上述中的退移形式图8(g)；

4) 发生侵蚀燃烧的单管内外燃装药燃面退移，可以用来检验上述中的退移形式图8(h)。

2.2 星形装药燃面退移

图9是计算采用的星形装药模型，装药几何参数如表1所示，装药两端面包覆不燃烧，星形界面按照平行层规律退移。

图9 星形装药模型Fig.9 Star grain modle

参数数值外径D/m0.269药柱长度L/m0.937药柱肉厚e1/m0.0565星角数n6星边夹角θ/(°)64.18角度系数ε0.88过渡圆弧半径r/m0.008星角圆弧半径r1/m0.008

提取各时刻垂直于装药轴线的横截面，可以看到LSM和MDF方法组合技术计算得到的燃面退移过程，如图10所示。从图10中可以看到：

1)星尖从凸曲面退移为凸尖点，且在初期星尖的角度不变，后期逐渐变大；

2)槽部的过渡圆弧逐渐变大；

3)星边初期一直保持为平面；

4)燃烧后期部分装药烧完，燃面与包覆层相交。

图10 星形装药燃面变化Fig.10 Change of burning surface in star grain

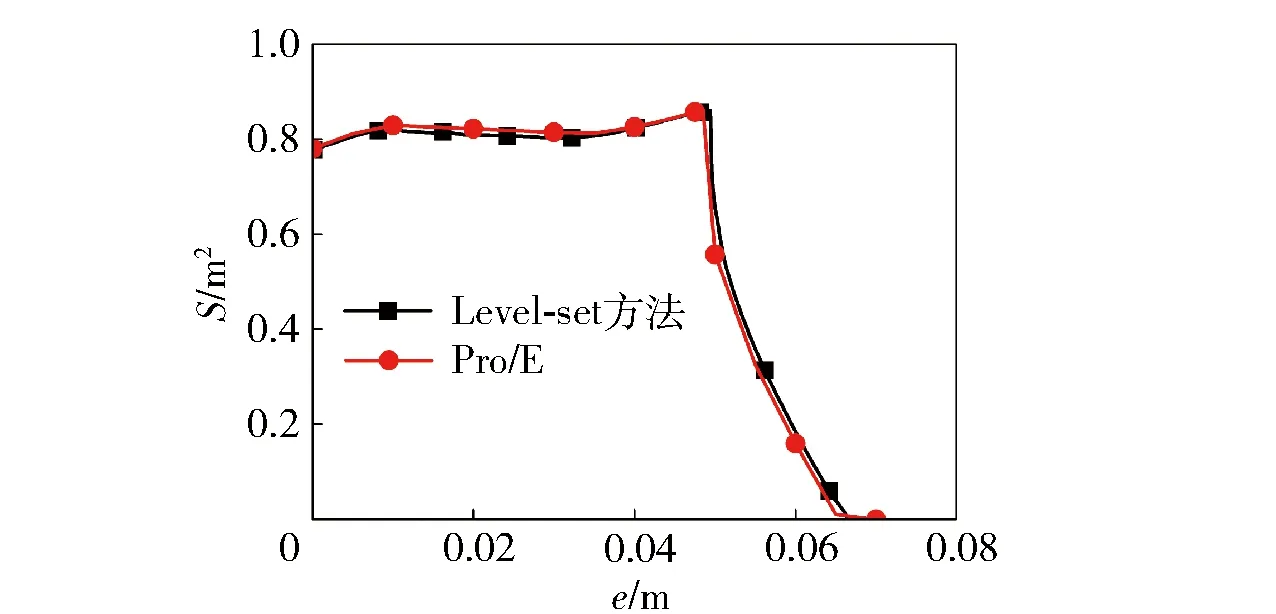
图11 星形装药燃面面积变化Fig.11 Change of burning surface in star grain

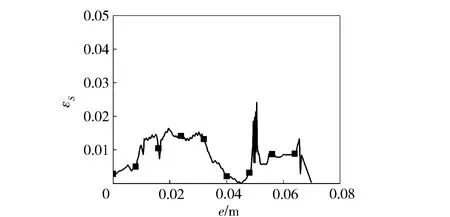
图12 燃面面积误差Fig.12 Deviation of burning area

对Level-set方法计算得到的Level-set函数场进行处理，采用1.4节描述的方法计算得到燃面面积S，如图11所示，将其与建模软件Pro/E输出的面积值相比，其面积误差εS曲线如图12所示。从图12中可以看到：Level-set方法计算燃面退移得到的燃面面积大小和建模软件输出的面积值是基本一致的，且误差最大不超过5%.

2.3 复杂三维装药燃面退移

图13为计算所采用的复杂三维药柱结构示意图，此药柱部分被包覆，部分裸露于燃气中，属于内外燃药柱，在此计算此药柱的燃面退移变化规律，检验在装药几何比较复杂的情况下Level-set和MDF组合方法计算燃面退移的准确性。

图13 复杂装药几何模型Fig.13 Geometrical model of complex grain

提取燃面退移过程中的燃面几何，如图14所示。从图14中可以看出药柱燃面的退移过程：1)初始时在药柱的内侧、两端及部分外侧都有燃面，此时燃面面积较大；2)随着药柱尾部燃烧殆尽，药柱变成近似短管形三维装药。

图14 装药燃面变化示意图Fig.14 Change of burning surface

计算Level-set和MDF组合方法得到的燃面面积，如图15所示。从图15中可以看出Level-set方法计算药柱退移的准确性：使用该方法计算得到的燃面面积与文献[26]给出的燃面变化曲线基本一致，说明Level-set和MDF组合方法可以准确地计算三维复杂装药的燃面退移。

图15 燃面面积变化曲线Fig.15 Curves of burning surface area

2.4 不同燃速推进剂组成装药的燃面退移计算

在此使用如图16所示的内外燃管形装药来验证Level-set方法和MDF方法组合技术是否能用来计算变燃速燃面退移，图16中药柱区域分为四部分，各个区域燃速各不相同，燃速之比分别为1.05∶1.10∶1.00∶1.15.

图16 不同燃速装药示意图Fig.16 Schematic diagram of grains with different burning rates

提取燃面退移过程中的燃面几何，如图17所示，图中Z、R分别为药柱长度和半径。从图17中可以看出燃面的变化过程：1)各区域处的燃面分别以各自对应的燃速退移，维持局部燃面的半径一致；2)在各区域交界处，由于两侧燃速不同，出现近似阶梯状曲面；3)燃速大的区域推进剂燃烧完后，总的燃面骤然减少，药柱可能存在脱落未燃尽的碎块。

计算Level-set和MDF组合方法求得的燃面面积，与燃速一致的装药燃面面积及文献[28]中提出的方法计算结果进行对比，如图18所示。图19为本文方法与文献中解析解的误差曲线。从图19中可以看到燃面面积的变化过程：1)在随着各区域装药燃烧完，燃面面积出现了多次明显降低，使得发动机工作末段与预期工作状态相差很大。如果不同批次推进剂的燃速存在明显差异将对发动机工作过程产生较大影响；2)在装药燃烧的前期，Level-set方法与解析解的方法相比误差在0.5%以下，在后期由于各区域推进剂先后燃尽，误差有所上升，但最大误差不超过5%.

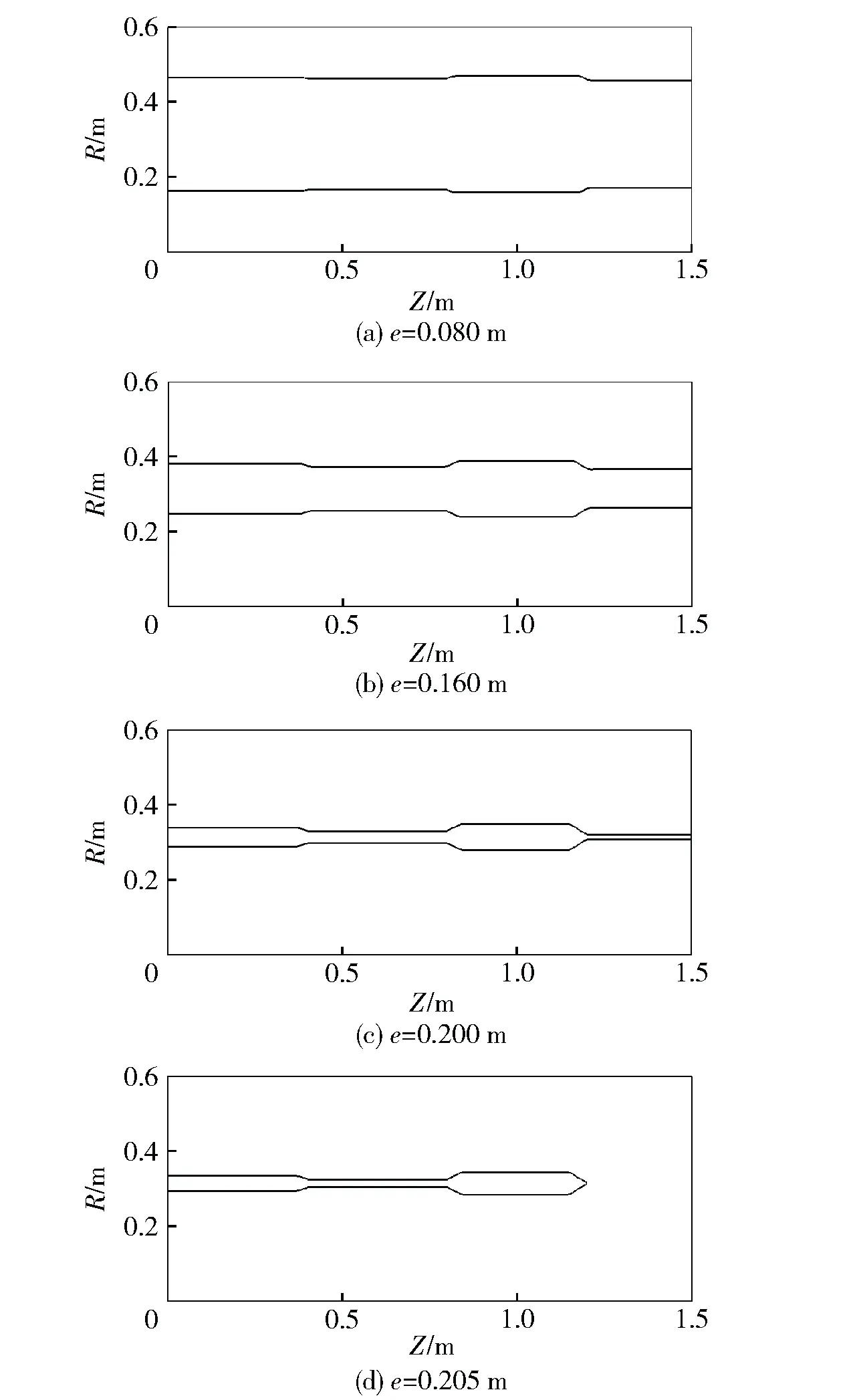
图17 不同燃速装药燃面变化Fig.17 Change of burning surfaces of grains with different burning rates

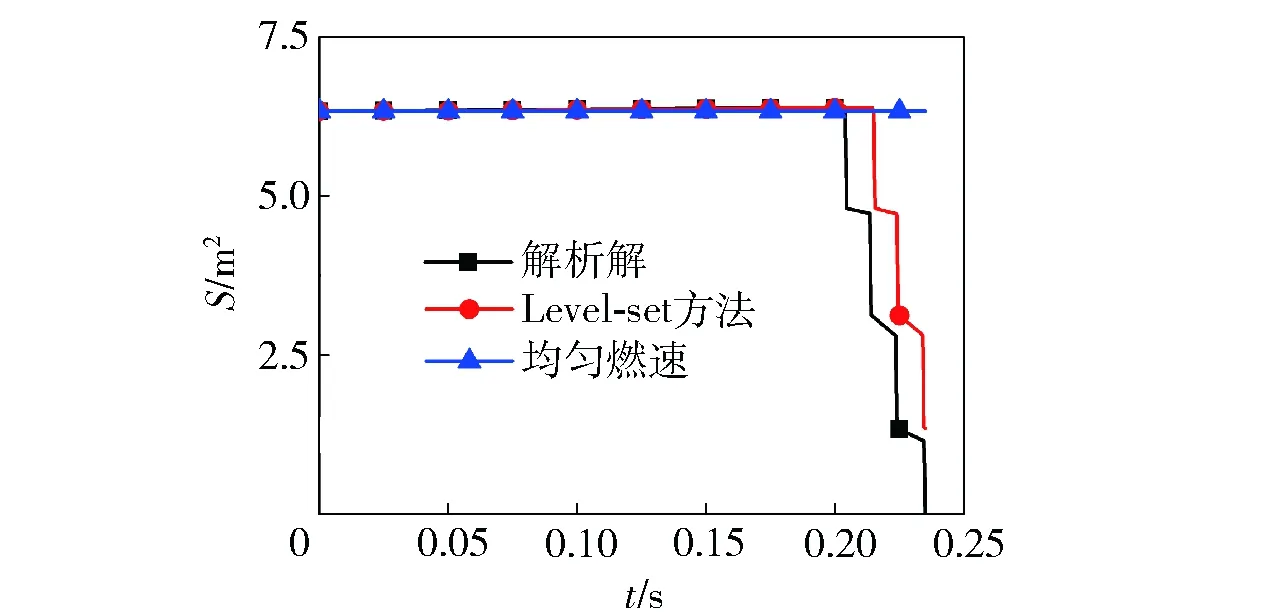
图18 变燃速装药燃面面积对比曲线(燃层厚度以燃速最低的区域计算)Fig.18 Comparison of burning surface areas with different rates (calculation of burning layer is based on minimum burning rate)

图19 燃面面积误差Fig.19 Deviation of burning area

2.5 侵蚀燃烧燃面退移计算

侵蚀燃烧效应指的是平行于装药燃烧表面的气体流动状态对装药燃速的影响。侵蚀燃烧效应使装药燃速增大，燃气生成率也随之增大，从而使燃烧室内燃气压强升高。在发动机工作初始阶段，装药通道截面积最小，气流速度大，侵蚀燃烧效应最严重。

侵蚀比ε通常被总结为关于喉通比J、密流G或燃通比等参数的经验公式，一般可以表示为如下形式：

(5)

式中：B表示喉通比J、密流G或者燃通比等参数；Bth表示发生侵蚀燃烧时参数B的临界值；K表示经验系数。

计算采用如图20所示的内外燃单管形装药，装药两端包覆，燃面为内外圆柱面，假定侵蚀燃烧只发生在燃通比比较大的管内燃气通道下游，且只发生在前期。侵蚀燃烧的计算需要和流场计算耦合，在此为了方便设置，在此并不进行与流场耦合的侵蚀燃烧燃面退移计算，而是根据侵蚀燃烧的特点，只进行类似于侵蚀燃烧形式的燃面退移计算。

图20 侵蚀燃烧模型示意图Fig.20 Schematic diagram of erosion combustion model

在此假定无侵蚀燃速r0为0.1 m/s，侵蚀比为采用如下形式：

(6)

提取各个时刻的燃面几何图，如图21所示。从图21中可以看到与实际侵蚀燃烧相类似的燃面变化趋势：1)管内燃气通道从某处开始一直到末端，因为侵蚀燃烧的影响，退移速度比上游大，且越靠近末端退移速度越大；2)装药后段比前段燃面退移速度大，形成一个近似锥面的曲面；3)内外燃面相遇，装药后段先烧完。

提取各个时刻的燃面面积，绘制曲线，与无侵蚀燃烧工况相比较，如图22所示。从图22中可以看到：1)在装药燃烧的前期，侵蚀燃烧使得装药燃面面积比无侵蚀工况要大，主要原因是侵蚀燃烧使得装药后段从圆柱面变为了锥面；2)在装药燃烧的后期，侵蚀燃烧使得装药燃面面积比无侵蚀工况小，主要原因是侵蚀燃烧使得装药后段提前烧完。

图21 侵蚀燃烧燃面变化图Fig.21 Change of burning surface with erosion combustion

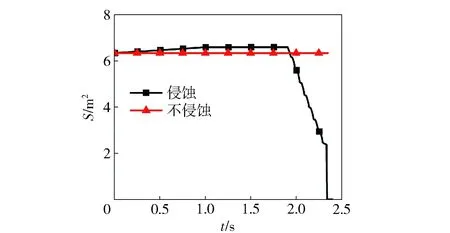
图22 侵蚀燃烧燃面面积对比曲线Fig.22 Comparison of burning surface areas in erosion combustion and normal combustion

综合侵蚀燃烧对燃速和装药燃面面积的影响，可以发现侵蚀燃烧会使发动机工作的初期压力明显高于无侵蚀时的压力预测值，研究侵蚀燃烧对发动机内弹道的影响有重大意义。

3 结论

通过上述对Level-set方法、MDF方法及其耦合算法和界面面积计算方法的介绍，对不同形式和不同情况下的装药进行计算分析可以得到以下结论：

1)Level-set方法和MDF方法组合技术可以比较准确地计算各种形式的燃面退移，包括平面燃面退移、凸曲面(凸尖点)燃面退移、凹曲面(凹尖点)燃面退移、装药部分包覆燃面退移、燃面以不同燃速退移和侵蚀燃烧燃面退移。

2)采用的面积计算方式可以比较准确地计算燃面面积，为瞬态内流场的计算提供了一个良好的基础。

目前本文燃面的耦合计算可以实现，并对不同结构的推进剂装药燃面退移过程进行有效的预测，但是由于所采用的MDF方法计算量较大，还需要对MDF计算进行一些技术上的改进，以期更快速、高效地进行燃面的耦合计算。

References)

[1] Peterson E G, Nielsen G C. Generalized coordinate grain design and internal ballistics evaluation program[C]∥Solid Propulsion Conference. Atlantic City, US: AIAA,2013:68-490.

[2] Coats D E, Levine J N, Nickerson G R. A computer program for the prediction of solid propellant rocket motor performance [R]. California: Ultra Systems Inc,1975.

[3] 侯晓,蹇泽群.三维药柱燃面的通用积分计算法[J]. 固体火箭技术,1993,9(3):1-6. HOU Xiao, JIAN Ze-qun. General integration calculation for burning surface of three dimensional grain[J]. Journal of Solid Rocket Technology, 1993, 9(3):1-6. (in Chinese)

[4] 周华盛.药柱通用坐标计算法计算结果跳动的原因分析及解决途径[J]. 固体火箭技术,1994,9(3):8-16. ZHOU Hua-sheng. Analysis and solution approach about pulsation cause of calculation results of the general coordinate calculation method of the grain[J]. Journal of Solid Rocket Technology, 1994,9(3):8-16. (in Chinese)

[5] 鲍福廷,李逢春.固体发动机装药CAD[J].固体火箭技术,1994,9(3):1-7. BAO Fu-ting, LI Feng-chun. Computer aided design of propellant grains for solid rocket motors[J]. Journal of Solid Rocket Technology, 1994, 9(3):1-7. (in Chinese)

[6] 田维平,王锟.固体发动机药柱CAD及燃烧模拟分析[J]. 固体火箭技术,1993,12(3):14-22. TIAN Wei-ping, WANG Kun. Computer aided design and burning simulation analysis of solid rocket motor grains[J]. Journal of Solid Rocket Technology, 1993,12(3):14-22. (in Chinese)

[7] 方蜀州,胡克娴.固体火箭发动机三维药柱燃面退移仿真技术及燃面通用计算方[J]. 固体火箭技术, 1993,12(4):10-20. FANG Shu-zhou, HU Ke-xian. The general technique of emulation and calculating of burning surface of 3D grain of solid rocket motors[J]. Journal of Solid Rocket Technology, 1993,12(4):10-20. (in Chinese)

[8] 颜仙荣,于胜春，王庆官.实体造型技术与固体发动机装药燃面计算[J].固体火箭技术,2003,26(2):20-22. YAN Xian-rong, YU Sheng-chun, WANG Qing-guan. The solid modeling technology and the grain-burning-area calculation[J]. Journal of Solid Rocket Technology, 2003, 26(2): 20-22. (in Chinese)

[9] 刘伟.基于Pro/E和Qt平台的固体火箭发动机内弹道性能计算[D].哈尔滨：哈尔滨工程大学, 2014. LIU Wei. Performance computing of solid propellant rocket motor[D]. Harbin: Harbin Engineering University,2014. (in Chinese)

[10] Voller V R, Brent A D. The modeling of heat, mass and solute transport in solidification systems[J]. International Journal of Heat and Mass Transfer, 1989, 32(9) : 1719-1731.

[11] Breton P L, Ribéreau D, Godfroy F. SRM performance analysis by coupling bidimensional surface burnback and pressure field computations[C]∥34th AIAA JPC Conference. Cleveland, US:AIAA, 1998.

[12] Gueyffier D, Roux F X. High-order computation of burning propellant surface and simulation of fluid flow in solid rocket chamber[C]∥50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference.Cleveland, US: AIAA, 2014.

[13] 沈伟,邢耀国.基于非结构网格的燃面推进算法[J]. 固体火箭技术, 2005, 28 (3):176-179. SHEN Wei, XING Yao-guo. A simulation method of burning surface regression based on unstructured mesh[J]. Journal of Solid Rocket Technology, 2005, 28 (3):176-179. (in Chinese)

[14] Jiao X M. Face offsetting: a unified approach for explicit moving interfaces[J]. Journal of Computational Physics, 2007, 220(2):612-625.

[15] 贺征,郜冶.动态网格在固体火箭发动机内流场计算中的应用研究[J].弹箭与制导技术, 2008,28(1):164-166. HE Zheng, GAO Ye. The study of dynamic grids application to calculate the inner flow field of solid rocket motor[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(1):164-166. (in Chinese)

[16] Li Q, He G Q. Coupled simulation of fluid flow and propellant burning surface regression in a solid rocket motor[J]. Computers & Fluids, 2014, 93(8):146-152.

[17] Sethian J A. Theory, algorithms, and applications of level set methods for propagating interfaces[J]. Acta Numerica, 1996, 5(5): 309-395.

[18] Hegab A, Jackson T L, Buckmaster J, et al. Nonsteady burning of periodic sandwich propellants with complete coupling between the solid and gas phases[J]. Combustion and Flame, 2001, 125(1): 1055-1070.

[19] 秦飞.固体火箭发动机复杂装药燃面算法研究[D]. 西安：西北工业大学,2003. QIN Fei. Method research for burning surface calculation of solid rocket motor with complicated grain[D]. Xi’an: Northwestern Polytechnical University, 2003. (in Chinese)

[20] Yildirim C, Aksel M H. Numerical simulation of the grain burnback in solid propellant rocket motor[C]∥41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Arizona, US: AIAA,2005:3995-4160.

[21] Cavallini E, Favini B, Di Giacinto M, et al. Internal ballistics simulation of a NAWC tactical SRM[J]. Journal of Applied Mechanics, 2011, 78(5): 748-760.

[22] Wang D H,Yang F, Fan H, et al. An integrated framework for solid rocket motor grain design optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(7): 1156-1170.

[23] Yao H H, Chiang C H. Tracking methods to study the surface regression of the solid-propellant grain[J]. International Journal of Engineering and Technology Innovation, 2014, 4(4):213-222.

[24] 何涛,孙振华.星型装药固体火箭发动机工作过程仿真研究[J].航空兵器,2015(1):61-64. HE Tao, SUN Zhen-hua. Numerical simulation of the working process in star grain solid rocket motor[J]. Aero Weaponry, 2015(1):61-64. (in Chinese)

[25] Michael A Willcox. Solid rocket motor internal ballistics simulation using three-dimensional grain burnback[J]. Journal of Propulsion and Power, 2007, 23(3):575-584.

[26] 马长礼.固体火箭发动机MDF燃面计算方法研究[D].长沙：国防科学技术大学, 2007. MA Chang-li. Research of MDF burning surface CaleUlation method for solid rocket motor[D].Changsha : National University of Defense Technology, 2007. (in Chinese)

[27] 熊文波,刘宇. 基于单元法的三维装药通用燃面计算[J]. 航空学报, 2009, 30(7):1176-1180. XIONG Wen-bo, LIU Yu. Generalized burning surface calculation of three dimensional propellant based on element method[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7):1176-1180. (in Chinese)

[28] 林小树, 王宝山. 双燃速固体火箭发动机内弹道计算方法[J]. 固体火箭技术, 1991 (4): 12-18. LIN Xiao-shu, WANG Bao-shan. Calculation method of solid rocket motor internal ballistic with dual burning rate[J]. Journal of Solid Rocket Technology, 1991(4):12-18. (in Chinese)

Research on Grain Burning Surface Regression Based on Level-set Method and Minimum Distance Function

WANG Ge, HAN Wan-zhi, LI Dong-dong, GAO Ye

(College of Architecture and Aerospace Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang， China)

The combustion surface regression is studied using Level-set method and minimum distance function (MDF) in SRM. A way that accurately predicts burning surface regression of solid propellant is established based on Level-set method and MDF. The grains with different geometries, the propellant grains with different burning rates and the grains with erosion combustion are calculated and analyzed. The results show that the combined method which calculates the burning area based on interface segmentation and geometric reconstruction has a good adaptability and high reliability on combustion surface regression.

ordnance science and technology; combustion surface regression; combustion surface area; level-set method; MDF method

2016-07-06

王革(1966—), 男, 教授, 博士生导师。 E-mail: wangge@hrbeu.edu.cn

V435+.12

A

1000-1093(2017)02-0280-12

10.3969/j.issn.1000-1093.2017.02.011