弹道中段目标进动周期的估计*

张艺瀛，高建军，李高鹏，郭汝江，蒋 坤

(哈尔滨工业大学 电子工程技术研究所，哈尔滨 150001)

弹道中段目标进动周期的估计*

张艺瀛*，高建军，李高鹏，郭汝江，蒋 坤

(哈尔滨工业大学 电子工程技术研究所，哈尔滨 150001)

为了克服循环平均幅度差函数法(CAMDF)估计弹道中段目标进动雷达散射截面(RCS)序列周期产生加倍误判的问题，引入了平均幅度差函数的凸包函数的概念，提出了凸包循环平均幅度差函数法(CHF-CAMDF)处理弹道进动目标的RCS序列，将处理后序列的最小谷值点所在位置与采样频率的商值作为所估计弹道目标的进动周期。相较于CAMDF，CHF-CAMDF在抑制加倍误判、抗噪性能以及序列长度敏感性三个方面都具有明显的优越性，能够有效地提取弹道中段目标的进动周期，提供了一种有助于真假弹头识别的可靠依据。

弹道导弹；目标识别；进动周期；凸包函数；循环平均幅度差函数

1 引 言

弹道中段的飞行距离远、时间长，占整个弹道导弹飞行时间的70%以上。这个阶段是弹道防御系统识别与拦截的重要阶段，基于提高导弹自身生存能力的目的，导弹飞行过程中一般会释放箔条、诱饵等假目标。为了保持姿态稳定，弹头在弹道中段一般保持进动状态。考虑到实际的投送成本，导弹在弹道中段释放的高仿真诱饵一般是充气型诱饵或刚性复制诱饵，也就是说诱饵和弹头在质量和质量分布方面存在较大差异，这种差异将导致两者在转动惯量上存在差异，使得高仿真诱饵的进动频率与真实弹头的进动频率差别明显。因而，有效地估计出弹道目标的进动周期有助于真假目标识别。

不少学者针对弹道目标进动周期的提取方法展开了研究。文献[1]中采用自相关函数法(Autocorrelation Function，AUTOC)与平均幅度差函数法(Average Magnitude Difference Function，AMDF)相结合的方法提取目标的进动周期，不过没有从根本上解决加倍误判的问题。文献[2]利用线性调频算法，通过控制时间采样间隔获取一维距离像序列，然后从一维距离像序列中提取目标的进动周期。文献[3]分析了采用循环平均幅度差函数(Circular Average Magnitude Difference Function，CAMDF)法估计进动频率产生加倍误判的原因，但是并没有针对性地提出当样本序列长度为周期长度的整数倍时抑制加倍误判的有效方法。文献[4]采用希尔伯特-黄变换处理雷达测量得到的窄带雷达散射截面(Radar Cross Section,RCS)序列获取目标的进动周期，这种频域处理方法的精确度受限于观测的时域数据长度。文献[5]采用快速傅里叶变换(Fast Fourier Transformation，FFT)在频域提取进动频率，不过由于FFT变换点数的限制有可能导致频谱泄露，文中为了抑制频谱泄露的出现进行了插值处理，而插值本身就是不精确的，插值方法的选取直接影响估计结果，说明该方法对进动频率估计不稳定。由上述分析可知，传统频谱分析法的局限性在于估计精度取决于观测的数据长度，要达到较高精度必须有较长的观测数据长度；时域周期提取函数的关键在于有效抑制分频和倍频所带来的误判。

为此，本文首先分析了进动目标RCS序列的周期特性，然后结合进动目标RCS序列的周期特性和AMDF的周期估计原理，提出了一种采用凸包削波法来改进CAMDF的新方法——凸包循环平均幅度差函数法(Convex Hull Function-Circular Average Magnitude Difference Function，CHF-CAMDF)。仿真结果表明，该方法提高了运算效率，有效抑制了倍频和分频误判的出现，具有较强的抗干扰能力，能够有效地从短时进动目标RCS序列中提取进动周期。

2 传统平均幅度差函数法

传统的平均幅度差函数定义为

(1)

当采用短时处理技术对目标信号进行加方窗处理后，式(1)变为

(2)

式(2)中：xw(n)=x(n)w(n)，

平均幅度差函数法周期估计其原理是当k0等于实际周期长度时候，|xw(n+k0)-xw(n)|为最小值，即D2(k0)为最小值。在较为理想的情况下，只要搜索到D2(k)的最小谷值点，就可以得到其周期的估计值，若采样频率为f0，则序列周期Te估计表达式为：Te=k0/f0。同理可知，ke=ak0,a=1,2,…时，当x(n)为严格周期信号时，即|xw(n+ke)-xw(n)|=0，则满足D2(k0)=D2(ke)。由以上分析可知，当ke=ak0时，易发生加倍误判。另外，由于随着滞后时间的增加，即k值的逐渐变大，求和项逐渐减少，导致D2(k)的值呈整体下降趋势，当下降到一定程度后，谷值点的清晰度检查变得较为困难，此时就会出现虚假谷值点，也会导致误判的发生。

为检验AMDF对于目标进动RCS序列的处理效果，建立如图1的弹头进动模型。图中:OA为目标对称轴,OM为进动轴，OS为进动轴OM在平面XOY的投影，α为进动角，β为姿态角，γ为进动轴与XOY平面的夹角，ω为自旋角速度，Ω为进动角速度。

图1 弹头进动模型Fig.1 Precession model of a warhead

仿真参数：关机点距离地面高度100 km，关机点速度4 500 m/s，关机点速度倾角30°，关机点方位角5°，关机点经度5°、纬度15°；雷达所在位置经度5°、纬度15°，雷达高度10 m，雷达频率1 GHz；弹头底部半径60 cm，端头半径5 cm，半锥角10°，进动频率10 Hz，进动角10°，采样频率10 Hz。由文献[6]可知，弹头的进动引起了姿态角的周期性变化，导致所观测到的弹头RCS序列呈周期性变化。根据文献[7]姿态角解算公式来求解弹道目标的姿态角，由文献[8]解算其RCS，考虑到动态RCS量测的误差，设各次量测是独立的，且量测的误差服从(u,σ2)的高斯分布，则当均值u=0 dBsm、方差δ2=0.25 dBsm时，提取其中60 s的RCS序列，并对其进行AMDF处理，如图2所示。

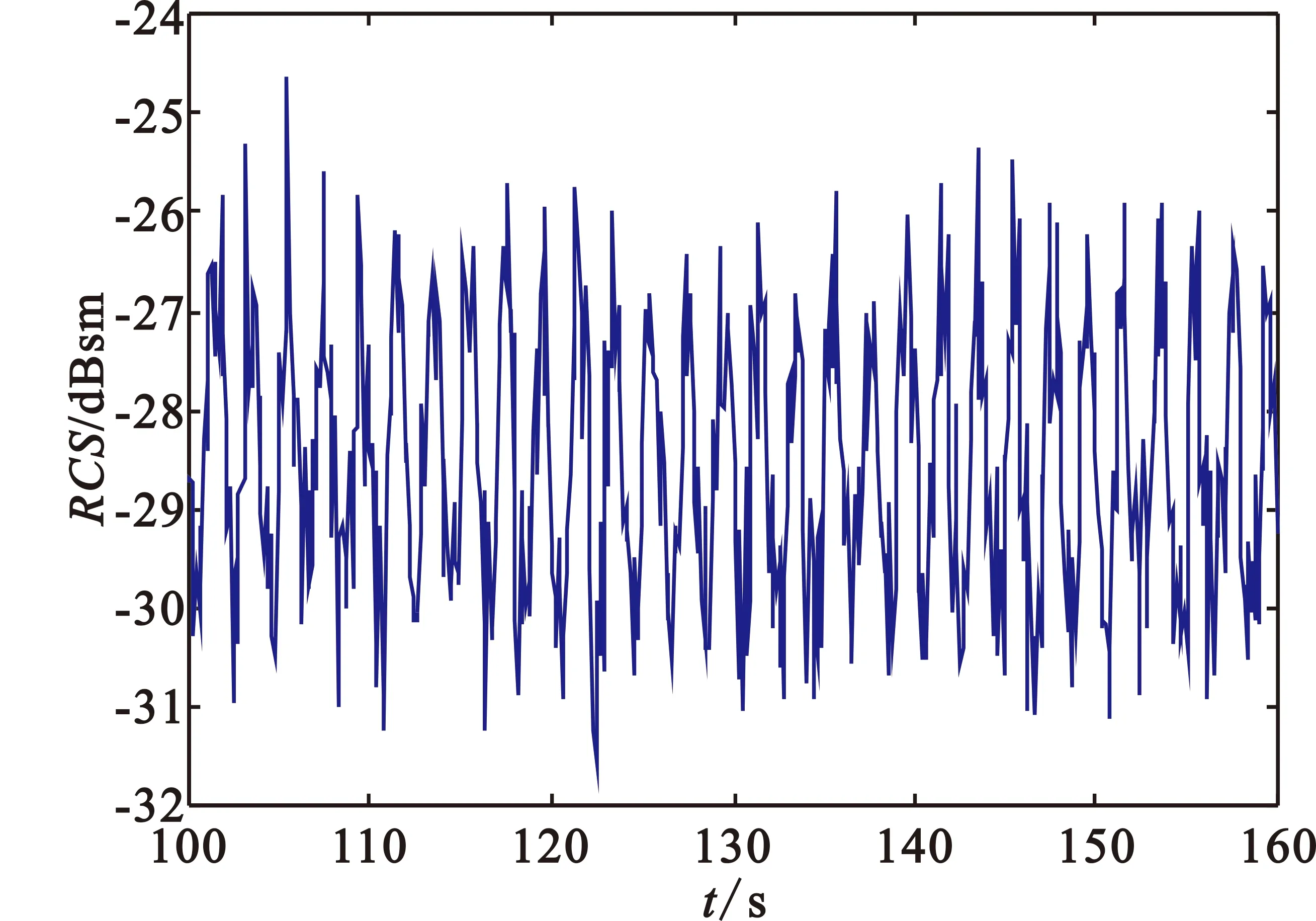
(a)进动目标RCS仿真序列

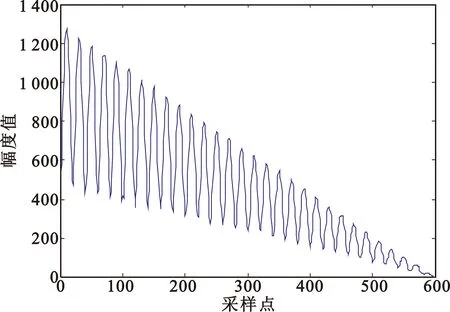
(b)AMDF处理结果图2 弹头RCS仿真及其AMDF处理Fig.2 RCS simulation and AMDF processing of a warhead

由图2可以看出，对于周期为2 s、采样频率为10 Hz的进动目标RCS序列，通过AMDF处理之后，出现3个特征，即AMDF的整体函数值呈下降趋势、谷值点处的谷值大小呈非严格减小趋势以及当时间滞后到一定程度后谷值点变得较为不清晰，出现虚假谷值点。这与以上对AMDF函数的分析结论完全一致。因而，如果依然提取最小谷值点进行周期估计时，必然会导致误判的发生。

3 循环平均幅度差函数法及其性质

为了克服传统AMDF随时间滞后幅度衰减的缺点，文献[9]提出了CAMDF。该方法采取类似循环卷积的方式对传统AMDF进行了重新定义：

(3)

式中：mod(n+k,N)表示对n+k进行模为N取余。

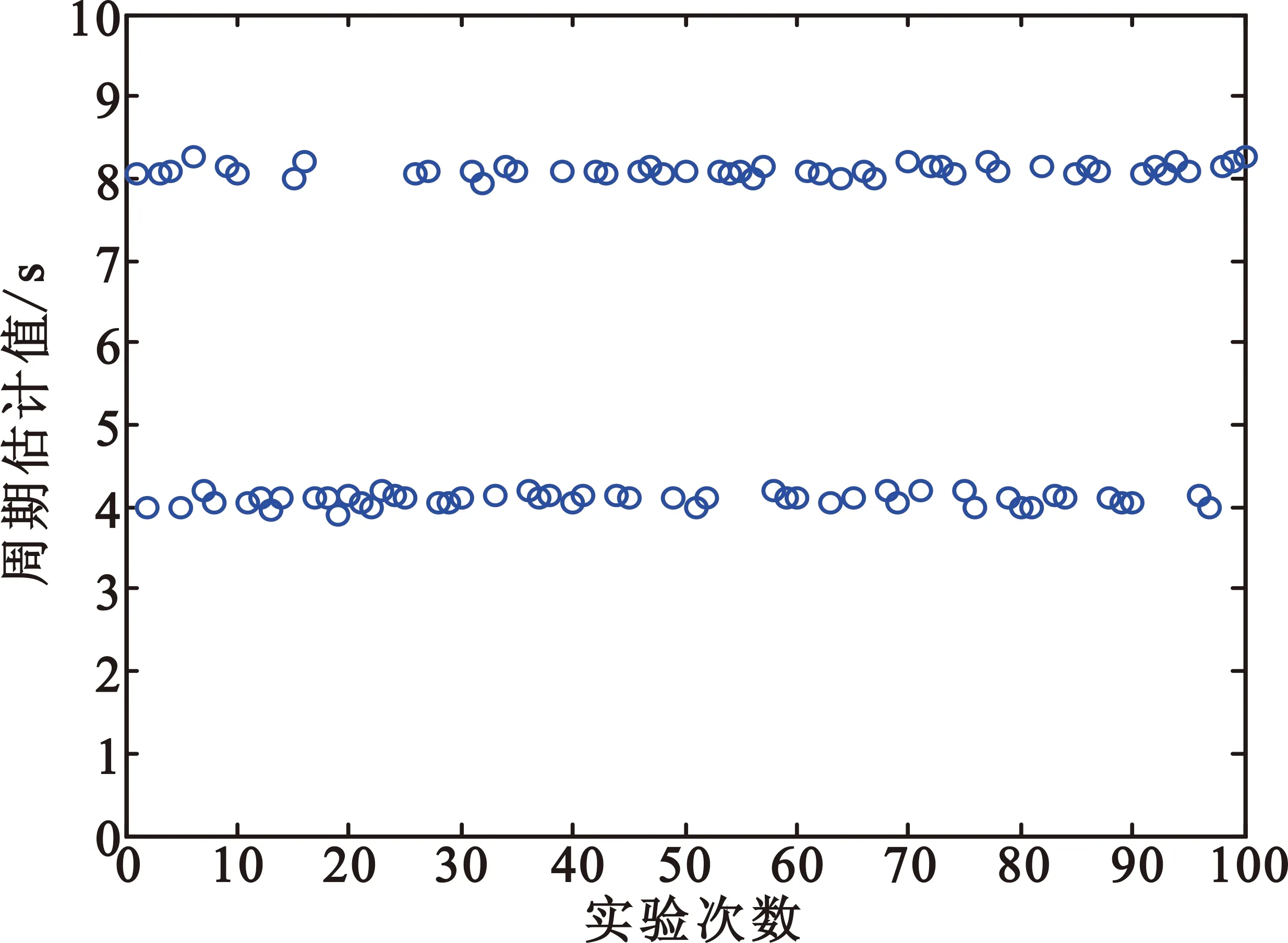
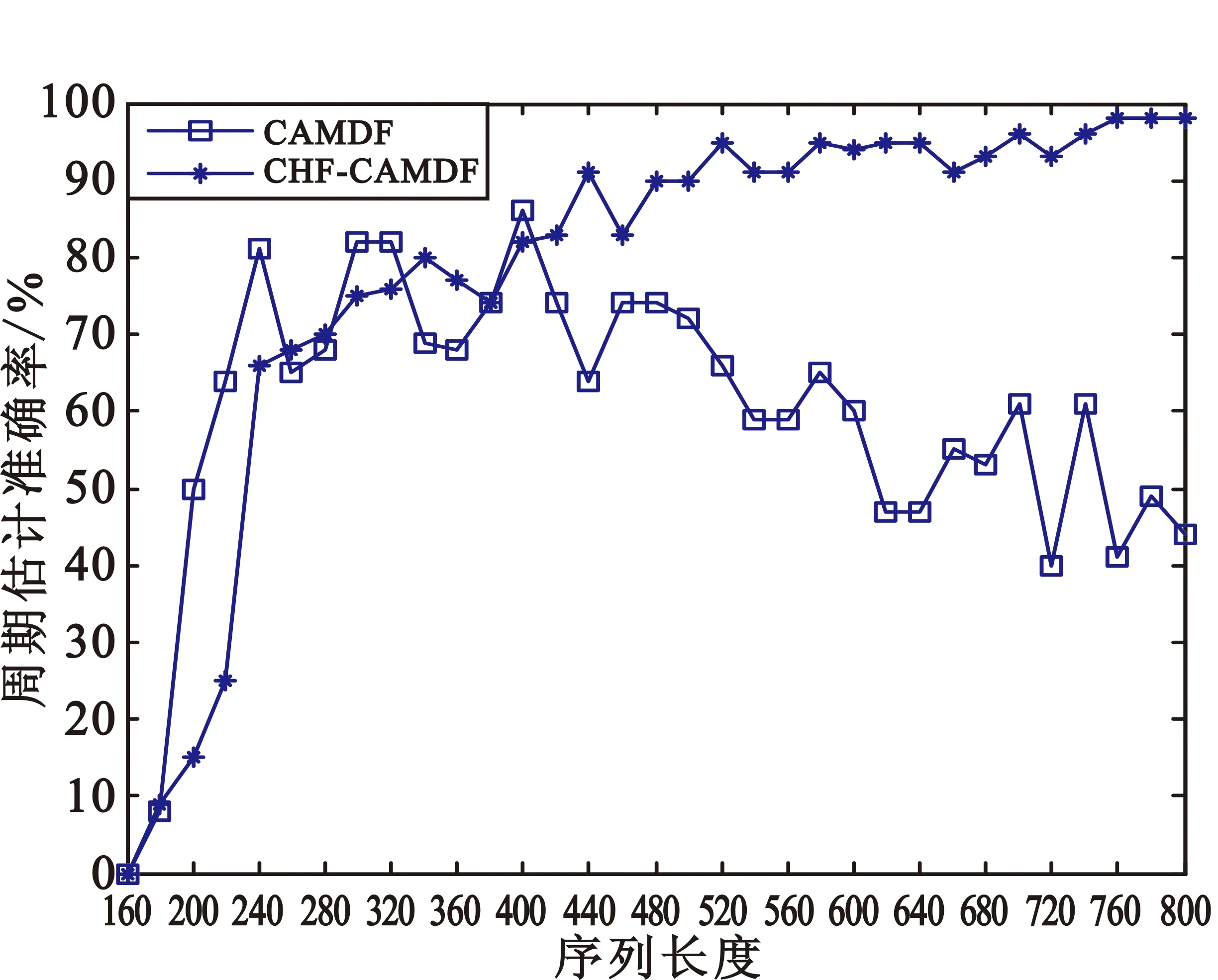
由文献[8]可知，当D(bT)

根据采样序列长度与实际周期长度T的关系，分两种情况进行讨论。

情况1 当N为T的整数倍时，即N=cT,c∈+且c≥2(b+1)，由定义知

(4)

由0≤n≤N-1，0≤bT≤⎣N/2」，则0≤n+bT<2N。下面根据n+bT与N的关系分3种情况讨论：

(1)当0≤n+bT

(5)

(2)当n+bT=N时，x(mod(n+bT,N))=x(0)，则

(6)

(3)当N

(7)

由式(5)～(7)，D(bT)可以表示为

(8)

同理，可得D(bT+T)的表达式为

(9)

当x(n)为严格周期序列时，由周期性可知，式(8)与式(9)相等，即

D(bT)=D(bT+T)=0。

(10)

当x(n)为周期性递减序列时，即满足x(n+kT)

D(bT)

(11)

情况2 当N为T的非整数倍时，即N=cT+m,0

(12)

(13)

证明过程同上，可得无论x(n)是严格周期序列还是周期性递减序列都满足

D(bT)

(14)

由以上推导可知，对于严格的周期序列，当序列长度为周期整数倍时，对于周期的估计会发生加倍误判；当序列长度为非周期整数倍时，则会避免加倍误判。而对于周期性衰减序列而言，无论采样序列长度是否为周期长度的整数倍，均能够很好地抑制加倍误判的发生。

4 改进的CAMDF算法

由于短时进动目标RCS序列呈明显的非平稳拟周期特性，如果用CAMDF估计其周期，为了抑制序列长度为周期整数倍时所发生的加倍误判，需将其转化为周期衰减序列。结合AMDF对于短时进动目标RCS序列的处理效果，本文在凸包概念的基础上，引入AMDF的凸包函数(Average Magnitude Difference Function - Convex Hull Function，AMDF-CHF)概念，具体定义如下：

设F(n)(0≤n≤N-1)是N点序列x(n)的AMDF，则函数

(15)

称为F(n)(0≤n≤N-1)的凸包函数。

由AMDF函数对短时进动目标RCS序列处理的效果以及AMDF-CHF的性质可知，函数φ(n)=F(n)-G(n)(0≤n≤N-1)具有非严格周期衰减性质，并且在序列周期整数倍附近的函数值为0，具有明显的周期界限。

图2 (a)中的目标进动RCS序列设为x(n)，图2(b)中的序列设为F(n)，则G(n)、φ(n)以及CAMDF处理结果如图3所示。

(a)凸包序列G(n)

(b)差值序列φ(n)

(c)CAMDF处理结果图3 改进的CAMDF算法的处理结果Fig.3 Processing result of the modified CAMDF algorithm

从图3可以看出，φ(n)总体呈非严格周期性衰减趋势，且具有明显的周期分界点，改进后的CAMDF算法依据最小谷值点的位置能够准确地判断出目标进动RCS序列的周期。

考虑到CAMDF依据最小谷值点进行周期估计，且最小谷值点位于第一峰值点之后，因而为了减弱毛刺点对周期判断的影响，进一步提高估计精度，可以从第一峰值点之后开始检测最小谷值所在位置。设序列x(n)的长度为N，采样频率为f，CAMDF处理后的序列第一峰值点位置为M，则最小谷值点位置k0满足k0∈(M,⎣N/2」)，则估计周期Te为

Te=k0/f。

(16)

由上所述，本文提出的CHF-CAMDF算法估计目标进动周期的算法步骤如下：

Step 1 对获取的进动目标RCS序列进行去噪预处理。

Step 2 对处理后的序列进行AMDF计算。

Step 3 将Step 2得到的序列进行CHF-AMDF处理。

Step 4 对Step 2和Step 3中得到的序列进行做差运算，得到相应的差值序列。

Step 5 对Step 4中的差值序列进行CAMDF处理，得到处理后的序列。

Step 6 对Step 5中得到的序列进行第一峰值点检测，然后搜索从第一峰值点直到序列长度一半区间范围内的最小谷值点位置。

Step 7 将Step 6中得到的最小谷值点位置除以采样频率，即为所估计的进动周期值。

5 仿真实验

仿真实验的目的是检验CHF-CAMDF和CAMDF对于不同进动目标、不同序列长度、不同噪声水平条件下的进动周期估计效果。进动目标选择钝头锥弹头和锥形诱饵，如图4；序列长度选择实际周期长度的整数倍和非整数倍；噪声选择不同分贝的高斯分布噪声。

(a)钝头锥弹头

(b)锥形诱饵图4 仿真目标Fig.4 Simulation target

建立进动模型(如图1)，相关参数同第2节。钝头锥弹头参数：弹头底部半径60 cm，端头半径5 cm，半锥角10°，进动频率0.25 Hz，进动角6°，采样频率20 Hz。锥形诱饵参数:诱饵底部半径40 cm，高114 cm，进动频率0.25 Hz，进动角8°，采样频率20 Hz。

为了检验CHF-CAMDF和CAMDF对目标进动RCS序列加倍误判抑制效果，随机选择仿真的序列长度为周期长度整数倍的640点采样序列，对所仿真的序列加上均值u=0 s、方差σ2=0.25 s的量测误差，进行100次蒙特卡洛实验，取其平均值作为估计的进动周期值，周期估计结果如图5所示。

(a)钝头锥弹头，CAMDF算法

(b)钝头锥弹头，CHF-CAMDF算法

(c)锥形诱饵，CAMDF算法

(d)锥形诱饵，CHF-CAMDF算法图5 基于不同算法的进动周期估计Fig.5 Precession period estimated by different algorithms

通过图5(a)和图5(b)以及图5(c)和图5(d)的对比可知，当采样序列长度为周期的整数倍时，采用CAMDF算法进行处理时，加倍误判较为严重，而采用本文提出的CHF-CAMDF算法进行处理时，能够有效抑制加倍误判的发生，且周期估计结果较为稳定。

为了检验CAMDF和CHF-CAMDF的抗噪声性能，本文在不同信噪比下进行了仿真实验，随机选择仿真的序列长度为周期长度整数倍的640点采样序列以及序列长度为周期长度非整数倍的670点采样序列，加上不同分贝的高斯白噪声，进行100次蒙特卡洛实验，取其均值作为实验结果，如图6所示(设相对误差在5%以内视为估计正确)。

(a)钝头锥弹头

(b)锥形诱饵图6 不同方法的抗噪性能比较Fig.6 Comparison of anti-noise performance among different algorithms

通过对图6分析可知，对于同一种目标，在相同条件下，本文提出的CHF-CAMDF算法的抗噪性能明显优于CAMDF算法；由于CAMDF算法无法抑制采样序列为周期整数倍时的加倍误判，所以在采样序列长度为周期整数倍和非整数倍两种条件下的估计准确率差异较大，反映了该算法的不稳定性；由于CHF-CAMDF算法有效地抑制了采样序列为周期整数倍时的加倍误判，所以无论采样序列长度与周期整数倍的关系如何，都不会影响算法抗噪性能的稳定性。

考虑到实际RCS序列采集的短时性，有必要检验CHF-CAMDF和CAMDF对于序列长度的敏感性。本文仿真的目标进动RCS序列周期为4 s，采样频率为20 Hz，即单个周期的实际长度是80个采样点。仿真实验设置如下：信噪比为20 dB，序列长度从第二个周期(160个采样点)开始，间隔步长20个采样点，到第十个周期(800个采样点)结束，共计33个样本点，对每个样本点进行100次蒙特卡洛实验，设实验结果服从正态分布(u,δ)，其中u为真实周期值，δ取0.5，当估计周期Te满足Te∈[u-δ,u+δ]时，视为有效估计结果，检测两种方法对序列周期的估计效果。实验结果如图7所示。

(a)钝头锥弹头

(b)锥形诱饵图7 不同方法的序列长度敏感性比较Fig.7 Comparison of sequence length sensitivity among different algorithms

从图7可以看出，由于受序列长度限制和噪声干扰，CHF-CAMDF和CAMDF在第二周期到第四周期内的估计效果差别不大。不过，随着序列长度的继续增加，CHF-CAMDF的优越性逐渐开始显现，在第四周期到第十周期内，CHF-CAMDF的估计效果大致呈温和振荡上升的趋势，且准确率较高，显示出了较强的稳健性；与CHF-CAMDF相比，CAMDF大致呈剧烈振荡下降的趋势，显示出了算法的极不稳定性。

6 结束语

本文通过建立弹道导弹的进动模型，对弹道中段目标进动RCS序列的特点进行了分析，并针对性地在CAMDF算法的基础上提出了估计目标进动周期的CHF-CAMDF算法。仿真实验表明，相较于CAMDF，CHF-CAMDF在抑制加倍误判、抗噪性能以及序列长度敏感性三个方面都具有明显的优越性，能够有效地提取弹道中段目标的进动周期。由于涉及军事背景，无法获取弹道中段目标的真实RCS信息，本文提出算法的处理的RCS序列都是基于目标的进动模型仿真得到的。在实际弹道中段，电磁环境的复杂性以及隐身技术的应用等会使得所探测的RCS序列与仿真得到的RCS序列存在差异，因而本文提出的算法在实际应用的效果还需要测试，如有必要，还需结合实际RCS序列的特点对算法进行改进。

[1] 赵炳秋，阳洪灿，吴垚. 弹道中段导弹目标进动特征提取方法研究[J].电光与控制，2016，23(7)：44-49. ZHAO Bingqiu,YANG Hongcan,WU Yao. Study on precession character extraction of ballistic targets in ballistic midcourse[J].Electronics Optics & Control,2016,23(7):44-49.(in Chinese)

[2] 何兴宇，童宁宁，胡晓伟,等. 利用HRRP序列提取弹道目标进动周期[J].现代防御技术，2015(4)：215-219. HE Xingyu,TONG Ningning,HU Xiaowei,et al. Precession period extraction of ballistic targets using HRRP series[J].Modern Defence Technology,2015(4):215-219.(in Chinese)

[3] 孙静. 一种基于改进CAMDF的进动周期估计方法[J].科学技术与工程，2015，15(27)：152-158. SUN Jing. Estimation of precession period based on improved circular AMDF[J].Science Technology and Engineering,2015,15(27):152-158.(in Chinese)

[4] 詹武平，陈剑军，刘利军. 利用雷达窄带RCS频域特性提取锥形目标进动参数[J].微型电脑应用，2015(3)：54-56.

ZHAN Wuping,CHEN Jianjun,LIU Lijun. Precession parameters extraction method for the target based on frequency character of radar narrow RCS[J].Microcomputer Applications,2015(3):54-56.(in Chinese)

[5] 胡杰民，付耀文，黎湘. 空间锥体目标进动周期估计[J].电子与信息学报，2008，30(12)：2849-2853. HU Jiemin,FU Yaowen,LI Xiang.Precession cycle estimation of cone-shaped spatial target[J].Journal of Electronics and Information Technology,2008,30(12):2849-2853.(in Chinese)

[6] 孟路稳，周沫，察豪,等.弹道导弹目标特性分析及雷达回波模拟[J].电讯技术，2015,55(2)：200-205. MENG Luwen,ZHOU Mo,CHA Hao,et al. Characterization analysis and simulation of radar echo from ballistic missile targets[J].Telecommunication Engineering,2015,55(2):200-205.(in Chinese)

[7] 孙佳佳，童创明，彭鹏,等. 弹道中段进动目标动态RCS仿真研究[J].科学技术与工程，2013，13(16)：4562-4566. SUN Jiajia,TONG Chuangming,PENG Peng,et al. Simulation of dynamic RCS data of coning targets in midcourse[J].Science Technology and Engineering,2013,13(16):4562-4566.(in Chinese)

[8] 黄培康，殷红成，许小剑. 雷达目标特性[M].北京：电子工业出版社，2005：86-99.

[9] 张文耀，许刚，王裕国. 循环AMDF及其语音基音周期估计算法[J].电子学报，2003，31(6)：886-890. ZHANG Wenyao,XU Gang,WANG Yuguo.Circular AMDF and pitch estimation based on it[J].Acta Electronica Sinica,2003,31(6):886-890.(in Chinese)

Precession Period Estimation of Ballistic Target in Midcourse

ZHANG Yiying,GAO Jianjun,LI Gaopeng,GUO Rujiang,JIANG Kun
(Research Institute of Electronic Engineering,Harbin Institute of Technology,Harbin 150001,China)

To solve the problem that double misjudgment is caused when the circular average magnitude difference function(CAMDF) is used to estimate the precession cycle of the radar cross section(RCS) sequence of the ballistic midcourse target,this paper introduces the concept of the convex hull function of average amplitude difference function and proposes the convex hull circular average magnitude difference function(CHF-CAMDF) to process the RCS sequence of the ballistic midcourse target,and the business value of the lowest valley location and the sampling frequency are estimated as the precession period of ballistic target.The simulation results show that CHF-CAMDF has obvious advantages in suppressing double misjudgment,anti-noise performance and sensitivity to the sequence length over the CAMDF. And CHF-CAMDF can effectively extract the precession cycle of the ballistic midcourse target,which provides a reliable basis for the identification of true and false warhead.

ballistic missile；target recognition；precession period；convex hull function；circular average magnitude difference function

2016-06-12；

2016-10-17 Received date:2016-06-12；Revised date：2016-10-17

总装备部预研基金项目

10.3969/j.issn.1001-893x.2017.02.016

张艺瀛，高建军，李高鹏，等.弹道中段目标进动周期的估计[J].电讯技术，2017,57(2):217-223.[ZHANG Yiying,GAO Jianjun,LI Gaopeng,et al.Precession period estimation of ballistic target in midcourse[J].Telecommunication Engineering,2017,57(2):217-223.]

TN959.1

A

1001-893X(2017)02-0217-07

张艺瀛(1993—)，男，河南人，硕士研究生，主要研究方向为雷达信号处理和雷达目标识别等；

Email:hitzyy@sina.com

高建军(1981—)，男，河北人，2010年于哈尔滨工业大学获博士学位，现为哈尔滨工业大学讲师，主要研究方向为雷达图像处理、雷达信号处理等；

李高鹏(1976—)，男，湖北人，副教授、硕士导师，主要研究方向为雷达信号处理、阵列信号处理和雷达目标识别等；

郭汝江(1976—)，男，黑龙江人，副教授，主要研究方向为雷达信号处理等；

蒋 坤(1992—)，男，四川人，硕士研究生，主要研究方向为阵列信号处理和雷达数据处理等。

*通信作者：hitzyy@sina.com Corresponding author：hitzyy@sina.com