基于PSO-BP算法的无线传感器网络定位优化*

卞国龙，黄海松，王安忆，于凯华

(1.贵州大学 现代制造技术教育部重点实验室，贵阳 550025；2.中国海洋大学 工程学院，山东 青岛 266100；3.国网山东省电力公司潍坊供电公司，山东 潍坊 261021)

基于PSO-BP算法的无线传感器网络定位优化*

卞国龙*1，黄海松1，王安忆2，于凯华3

(1.贵州大学 现代制造技术教育部重点实验室，贵阳 550025；2.中国海洋大学 工程学院，山东 青岛 266100；3.国网山东省电力公司潍坊供电公司，山东 潍坊 261021)

在研究现有定位算法的基础上，针对基于接收信号强度指示(RSSI)定位模型中的参数易受环境影响等问题，提出了一种新型的粒子群优化(PSO)算法与后向传播(BP)神经网络相结合的算法。BP网络算法权值的修正依赖于非线性梯度值，易形成局部极值，同时学习次数较多，需先通过粒子群算法进行优化。为了提高定位精度，首先采用速度常量法滤波处理，然后通过改进的混合优化算法对BP神经网络初始权值和阈值进行优化，并分析算法的性能。试验中隐层节点个数采用试错法，从12到19变化，以确定合适数目。实验结果表明，与一般加权算法和传统BP算法相比，改进的混合优化算法可大幅改善测距误差对定位误差的影响，同时可使25 m内最小定位误差小于0.27 m。

无线传感器网络；定位算法；测量误差；BP神经网络；粒子群优化；路径损耗模型

1 引 言

随着无线传感网络的发展，人们对定位技术的需求不断提升。定位算法主要分为两类:一类为基于测距的定位算法，如接收信号强度指示(Received Signal Strength Indication，RSSI)算法、TOA(Time of Arrival)算法等；另一类为基于非测距的定位算法，如APIT(Approximate PIT Test)、DV-Hop(Distance Vector-Hop)等。针对无线节点定位的难点问题，许多学者和专家进行了大量的研究工作，提出了许多定位优化算法。方震等通过分析RSSI测量值的变化，采用均值和加权法降低环境的影响，但忽略了路径衰减指数误差的影响，不能很好地适应实际条件[1]。加州大学Chris Savarese等提出了一种Two-phase positioning循环求解算法，首先求节点粗略坐标，然后循环求精，可以提高精度，但无法消除RSSI测距误差对定位计算的影响[2]。邹冈等对粒子滤波法改进，采用动态分簇结构网络，分别用并行粒子滤波法和信息粒子滤波法进行分布式估计，能节约通信能耗，但频繁重抽样去除权重值较小的粒子，导致粒子退化，影响精度[3]。

针对上述存在的问题，本文采用RSSI算法，利用路径损耗(Path Loss)模型将RSSI值转换为距离值。BP神经网络是一种自学习的智能网络，在许多领域得到应用。在现有的BP神经网络中，常通过梯度信息修正权值，易获得局部极值。现将粒子群优化(Particle Swarm Optimization,PSO)算法应用到BP网络中，利用其收敛速度快、全局搜索能力强的特点以及改进的PSO算法群体并行搜索的特点，寻找合适的BP网络初始权值和阈值。本文提出的PSO-BP网络收敛速度更快，可以进行大范围数据融合，减少环境对计算的影响，提高算法的稳定性和精度。

2 定位算法基础

2.1 RSSI算法测距原理

无线信号易受环境影响，常用的模型有自由空间传播模型、对数模型等，其中对数模型使用范围较广。模型参数通常由经验法测得，但在不同的环境下需对参数修正[4]。对数模型能测量当距离为d时接收功率P(d)。P(d)相对于P(d0)的计算式为

(1)

式中：P(d0)为参考距离d0处的信号强度；P(d)为d处信号强度；n为路径损耗指数，由环境决定。本文采用简化的对数距离路径损耗模型，对式(1)两边取对数并进一步优化得

(2)

根据接收到RSSI值和传播损耗模型，由式(2)发射点和接收节点间的距离可由下式求得:

(3)

2.2 改进的速度常量滤波优化

首先采用速度常量滤波算法对RSSI值进行处理。速度常量滤波法是考虑物体在运动范围内移动位置间有关联，前一刻位置和当前位置存在关系，采用速度常量使移动点某一时刻保持匀速运动以达到滤波效果，并以其值作为测试结果进行初步处理[5]。其分为估计测量阶段和预测计算阶段两部分，其中估计测量阶段为

(4)

式中：Rpv(i)为i时RSSI的测量值,Rpd(i)为i时刻RSSI的预测值,Re(i)为i时刻RSSI滤波值,Vpd(i)为i时刻RSSI变化率的预测值,Ve(i)为i时刻RSSI变化率的滤波值,ts为采样时间间隔,a和b为增益常量。预测计算阶段为

(5)

式中：Rpd(i+1)为i+1时刻RSSI的预测值,Vpd(i+1)为i+1时刻RSSI变化率的预测值。

速度常量滤波算法比较简单易实现，抑制作用明显，能够有效减小信号波动带来的影响，也能够较好地解决RSSI值的随机性干扰问题。

3 定位算法的优化

3.1 改进粒子群算法的处理

粒子群算法随机初始化一群粒子，每个粒子看作一个解。在每次迭代中，粒子对两个值更新，一个为全局适值Pg=(P1g,P2g，…，Ptg)，另一个为个体适值Pm=(P1m，P2m，…，Ptm)。

(1)在T维空间中，用Vi(k)=(vi1(k)，vi2(k)，…，vid(k))和Xi(k)=(xi1(k)，xi2(k)，…，xid(k))分别表示粒子i在第k次迭代时的速度和位置[6]。粒子在下一次搜索中找到Pm，位置和速度的更新公式分别为

Xi(k+1) =Xi(k) +γVi(k+1)，

(6)

Vi(k+1) =ωVi(k) +μ1rand(0,1)1(pmd-Xid(k))+μ2rand(0,1)2(pgd-Xid(k)) 。

(7)

式中：Xi(k+1)为下一刻位置；Vi(k+1)为下一刻速度；γ为约束因子；μ1和μ2为加速常量，值为1.52；rand(0,1)1和rand(0,1)2为独立的随机数；ω为惯性权重。粒子群算法利用粒子自身信息、个体适值和全局适值确定下一步位置，为正反馈，易获得局部极值。所以在t时刻，粒子位置Xid(k)可以通过蒙特卡洛(Monte Carlo)法优化[7]：

(8)

可由下式确定粒子k+1时刻位置：

(9)

式中：α、β为[0,1]间的随机数；X0(k)为随机初始位置参数；γ为收缩扩张系数，控制算法的收敛速度；L为k次迭代后的特征长度参数。T维空间的速度V表示粒子位置变化的概率值，而不是连续空间中的速度，可以用以下矩阵表示：

(10)

式中：vkn∈[-vmax，vmax]，k∈{1，2，…，g}，n∈{1，2，…，h}，V取值范围为[0，1]。

(2)惯性权重ω是粒子群算法中的重要参数，较大的ω有较强的全局搜索能力，但局部搜索能力会有所下降：

(11)

式中：ωmax、ωmin分别为惯性权重最大值和最小值，randn(0,1)为服从标准正态分布的随机数。Shi等[8]提出了一种线性递减模型，ω采用从0.9～0.4的线性方式递减：

ω=ωmax-c(ωmax-ωmin)/cmax。

(12)

式中：c为当前迭代次数,cmax为最大迭代次数。为了提高局部和全局搜索能力，构造出了ω非线性递减模型：

ω=ωmin+(ωmaxωmin)exp[-1/(1+1+c/cmax)] 。

(13)

(14)

(15)

式中：Δ(v，y)的表达式为

Δ(v，y) =y×(1-s(1-c/cmax)θ)。

(16)

式中：θ为非一致性程度，其在[2，5]范围内取值；s为[0，1]内的随机数。该调整能使粒子尽快跳出局部极值区域，提升收敛速度。

(3)适应度函数引导粒子的搜索方向，需要由误差进行计算。可设二维空间中移动点坐标为(x,y)，n个参考点的坐标分别为n1(x1,y1)，n2(x2,y2)，…，nn(xn，yn)。移动点到参考点距离为di，由于误差，di与计算值不相等。为了减小误差累积，将距离的的估算值与实际值的均方根误差作为适值函数。误差方程为

(17)

式中：(xi,yi)表示第i个参考点坐标；n为目标点邻近参考点数目，n≥3。在优化计算结果的基础上，为了再次平衡全局和局部搜索能力，需对ω进一步优化，在每次迭代中由下式确定权值：

(18)

式中：ωmin=0.4；ωmax=0.9；根据计算可得粒子当前的适值f；根据所有粒子的当前适值，可计算平均适值fh和最小适值fmin。

3.2 BP神经网络算法的优化

BP网络是一种按误差逆传播算法进行训练的网络，对BP网络训练时，当所有实际输出与理想输出相同时停止训练，否则要对权值进行修正。随机生成一群粒子Xi(t)=(wi1(t)，wi2(t)，…，wis(t))，网络输入层的输出和输入相同[10]。选择3层的BP网络，包括输入层h、隐含层数j、输出层u，那么隐层各节点的输入为

(19)

式中：ηw为隐层的阈值，w∈{1，2，…，j}；qiw为输入层至隐层的权值。信息首先由输入层经由Sigmoid激活函数f(x)=1/(1+e-x)传至隐层：

(20)

即可得隐层的输出为

(21)

式中：h为输入点个数，Gw为接收的刺激总和，Uw为隐层第w个神经元的输出。输出层有u个神经元，那么输出层的输入和输出分别为

(22)

(23)

式中：rwk为隐层至输出层的权值，Sk为接收刺激的总和，j为隐层节点数，Fi+1为输出层输出，ck为输出层阈值。BP网络在训练前将各层的权值和阈值初始化为[0，1]，这种随机初始化会使收敛速度较慢且不易获得最优解[11]。定义在训练样本(xk，yk)上的误差为

(24)

式中：Fk为输出层第k个节点的输出，u为输出层个数。输出层权值按下式更新：

rwk(t+1)=rwk(t)+Δrwk(t)。

(25)

在反向传播中，一般的BP算法沿目标函数下降最迅速的方向即负梯度方向调整权值，输出层权值的变化与误差函数对输出层权值的负梯度正相关：

隐层的权值按下式进行更新：

qiw(t+1)=qiw(t)+Δqiw(t)。

(26)

隐层权值沿负梯度方向的变化进行调整：

式中：η为学习率，η∈(0,1)。由上文可知，权值的修正完全依靠梯度值，这种优化方式易形成局部极值，而且训练次数较多，使收敛变慢[12]。同时，增加权值与阈值的平方和，训练会倾向较小的权值和阈值，使输出光滑，则误差函数改为

(27)

式中：n为样本数；qiw表示连接权和阈值；Ek表示第k个样本的误差；ξ为网络复杂度与经验误差的折中系数，由交叉验证法估算，ξ∈(0,1)。

3.3 PSO-BP神经网络算法优化

首先,确定网络结构，用前向算法计算每组训练样本的输出，用PSO算法搜索出使适值最小的位置。然后，用PSO算法训练BP网络，将粒子的当前位置Xi作为权值和阈值，将BP网络的误差作为PSO算法的适值，更新粒子。PSO-BP网络的计算步骤如下：

步骤1 根据神经网络类型和节点数目得到样本，对BP网络的参数初始化，把BP网络初始的权值和阈值作为PSO算法的一组初始粒子群。

步骤2 初始化粒子群的参数，包括学习因子、种群规模、迭代次数，根据变量的可能取值范围设定粒子的范围和速度。

步骤3 计算粒子的适值。根据输入输出样本计算每个粒子位置对应的适应值，根据初始粒子适应值确定个体适值和种群适值。

步骤4 确定评价函数。用PSO代替BP网络的初始寻优，在已接近最优解的基础上寻优，以式(27)作为寻优目标。当式(27)达到最小值时搜索出最佳权值和阈值。在每一次迭代中，根据新粒子适值更新粒子个体适值和全局适值。

步骤5 判断是否达到条件。假如迭代次数达到最大值或满足误差要求，停止迭代，否则转至步骤4。

步骤6 满足条件后，将获得的最优值对BP网络权值和阈值赋值，利用BP算法训练网络，然后输出最优解。

PSO-BP网络算法流程如图1所示。

图1 PSO-BP算法流程图Fig.1 Flow chart of PSO-BP algorithm

3.4 算法训练结果分析

为了使计算合理，输入为接收到的5个RSSI值，即网络输入层h为5，输出层u为5。采用试错法对隐层个数进行选取，实验结果如表1所示。经过比较后设定粒子数为n=50，惯性权重ω=0.6，学习因子μ1=μ2=1.52。表1是预测结果在隐层神经元个数不同时的训练结果，300次结果中能达到训练目标的为收敛成功。由表1可看出，相比于BP网络算法，该定位方法训练收敛时间短，定位结果稳定;当隐层个数为17时，训练误差最小，收敛成功率高，且训练次数较少，因此确定隐层节点个数为17。

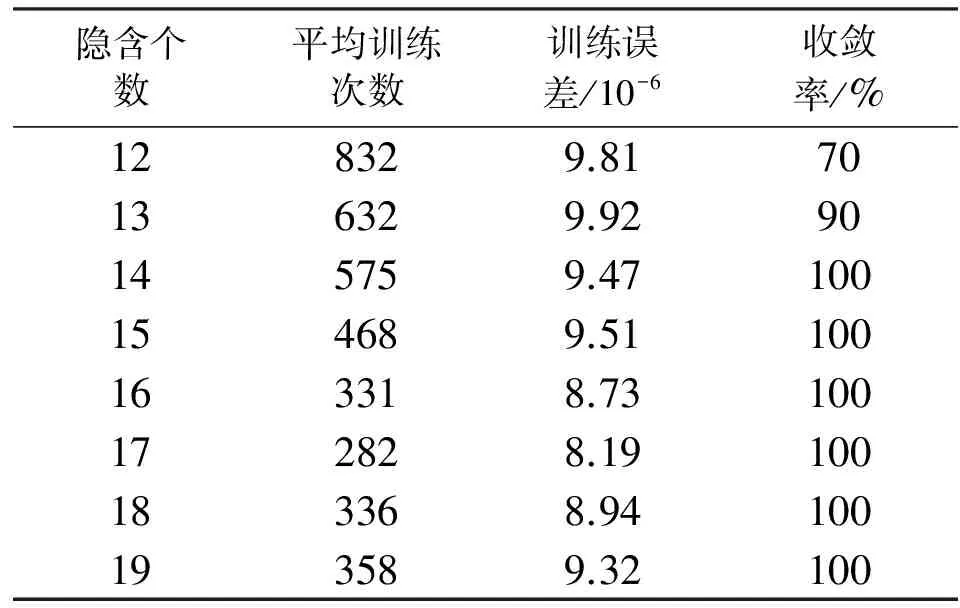
表1 隐层神经元个数对误差预测的影响Tab.1 Effect of the number of hidden layer neurons on the error prediction

将优化好的权值和阈值作为BP网络的初始权值和阈值进行训练，取隐层神经元数为17，训练次数为200，收敛精度设置为10-6时，训练结果如图2所示，可见满足要求。

图2 PSO-BP网络训练结果统计图Fig.2 PSO-BP network training results statistics

4 实验结果分析与统计

4.1 实验二维图与结果

为了进一步验证改进PSO-BP算法的性能，以实验室的部分区域作为试验区进行验证，实验区域为25 m×25 m，参考点数为6，节点通信半径R为20 m，节点随机地布置在定位区域内，如图3所示。不同编号节点在多次测量后的定位误差如表2所示，可知改进PSO-BP网络算法的定位误差相对变化较小，可以较好地提高定位精度。

图3 试验布置二维图Fig.3 Layout of the two-dimensional map

节点编号坐标/m加权质心算法改进PSO-BP算法实际测值误差/m加权质心算法改进PSO-BP算法1(4．1，4．2)(2．4，2．2)(3，3)1．631．032(6．7，22．4)(6．4，23．6)(6，24)1．740．763(8．4，21．9)(9．2，20．8)(9，21)1．070．274(11．2，19．4)(11．3，18．7)(12，18)1．540．985(14．2，15．5)(15．5，15．8)(15，15)0．990．876(18．7，10．9)(18．3，11．6)(18，12)1．260．497(20．5，22．4)(21．9，21．7)(21，21)1．301．10

4.2 测距误差与定位精度的关系比较

针对RSSI算法的测距会受环境影响的问题，由图4可知，随着测距误差的增大，定位误差也会增加，但PSO-BP算法比现有BP算法会进行更合理修正，降低了测距误差的影响，在相同的测距误差时PSO-BP算法的定位误差明显受影响较小，尤其当测距误差较大时，改进算法的抗误差性能更强。PSO-BP算法有效解决了传统BP算法测距修正的的局限性，在测距误差较大时也保持了较好的精度。

图4 测距误差对定位误差的影响Fig.4 Effect of ranging error on positioning error

4.3 不同的通信半径下的误差分析

试验区域为60 m×60 m，区间布置25个移动节点，7个参考点，不同的通信半径R下3种算法的定位误差如图5所示。R值相同时，现有BP算法的平均误差比改进的PSO-BP网络算法大，两种算法的误差最大相差0.273 m。随着R值增大，现有BP网络算法的误差变化会变小，一直处在0.281～0.429 m之间，但改进PSO-BP算法的误差随着通信半径增大误差减小效果更加明显。

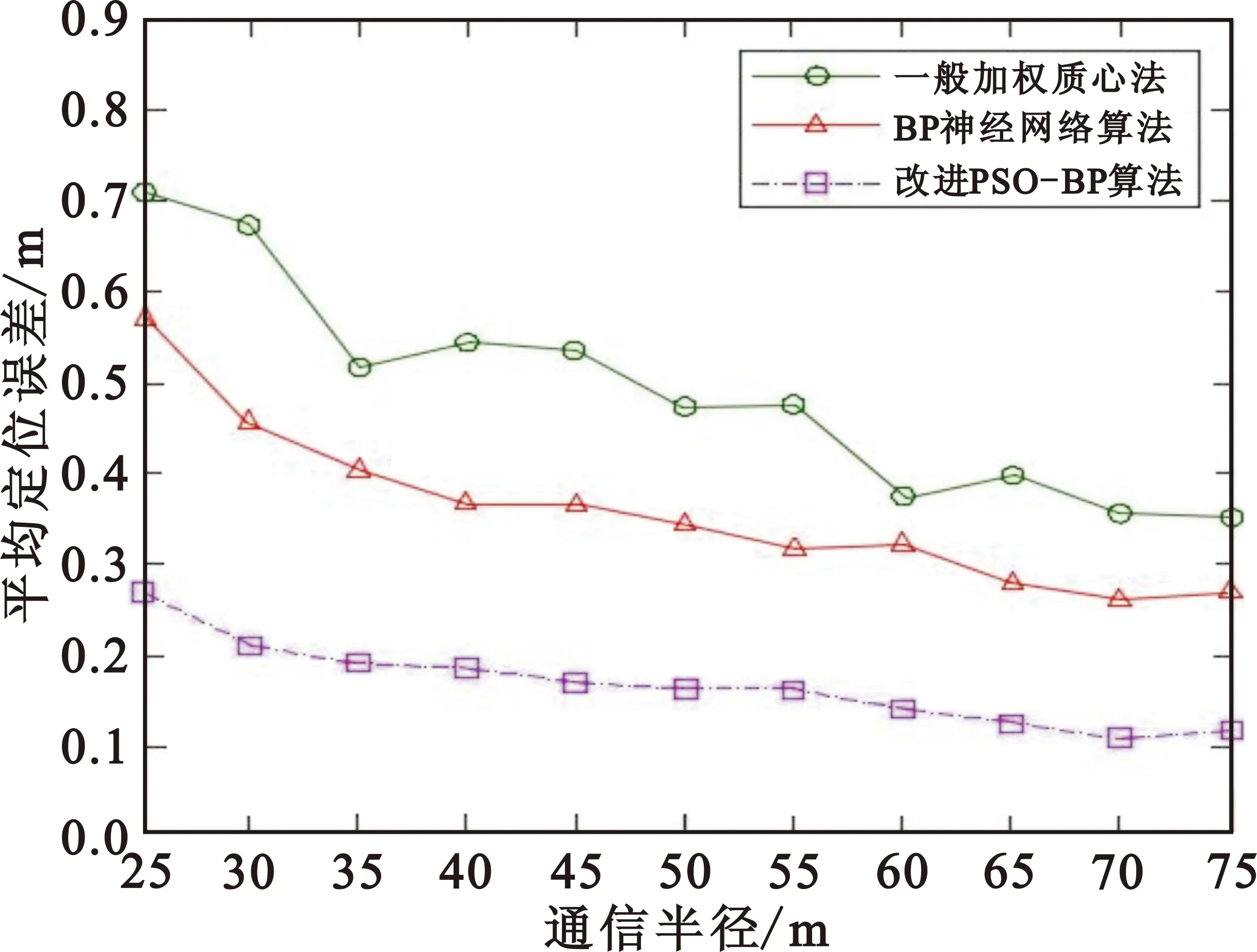
图5 不同通信半径下定位误差对比图Fig.5 Comparison of location error under different communication radius

5 结束语

BP网络算法是一种局部搜索算法，根据误差的反向传播修正权值和阈值，易获得局部极值，同时反向传播训练次数会较多。为了改进BP网络，本文提出利用PSO-BP网络优化RSSI值，然后对RSSI值进行处理，最后得到相应的距离数据。在新算法中PSO算法与BP算法结合，即用改进的粒子群算法对神经算法的权值训练形成一种新的算法，可以避免局部极值。在实验过程中，一些定位节点存在个体差异，精度始终较低。PSO-BP算法能得到理想的效果，具有局部搜索和全局搜索最优解的优势，增加了BP算法收敛速度和全局收敛性，提高了BP网络的学习能力，但在实际应用中，对如何确定一个合适的神经网络没有准确的理论指导，只能通过实验不断调整合适的网络结构。

[1] 方震,赵湛,郭鹏,等.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530. FANG Zhen,ZHAO Zhan,GUO Peng,et al.Analysis of distance measurement based on RSSI[J].Chinese Journal of Sensors and Actuators,2007,20(11):2526-2530.(in Chinese)

[2] SAVARESE C，RABAEY J，LANGENDOEN K.Robust-positioning algorithms for distributed ad-hoc wireless sensor network[C]//Proceedings of the USENIX Technical Annual Conference.Monterey:USEIX Press，2002:317-327.

[3] 邹冈,石章松,刘忠.传感器网络中的分布式粒子滤波被动跟踪算法比较研究[J].传感技术学报,2007,20(6):1344-1348. ZOU Gang, SHI Zhangsong, LIU Zhong.Comparative study of passive tracking algorithm for distributed particle filter in sensor networks[J].Chinese Journal of Sensors and Actuators,2007,20(6): 1344-1348. (in Chinese)

[4] GIORGIO Q,RICCARDO M,GIANLUIGI P,et al. Sensing,compression and recovery for WSNS:sparse signal modeling and monitoring framework[J].IEEE Transactions on Wireless Communications,2012,11(10):3447-3461.

[5] 江春冬,惠慧,陈云飞,等.与强度无关的位置指纹在线定位改进算法[J].电讯技术,2016,56(2):128-134. JIANG Chundong,HUI Hui,CHEN Yunfei,et al. An improved algorithm for online location fingerprint location independent of intensity[J].Telecommunication Engineering,2016,56(2):128-134.(in Chinese)

[6] AHMAD EI A,SLIM Z,SOFIENE A,et al. Low-cost localization for multi-hop heterogeneous wireless sensor networks[J].IEEE Transactions on Signal Processing,2015,13(7):1199-1212.

[7] CARLOS F,JOSE L,INMACULADA M.Time-space sampling and mobile device calibration for WIFI indoor location systems[J].IEEE Transactions on Mobile Computing,2011,10(7):913-926.

[8] SHI Y,EBERHART R.A modified particle swarm optimizer[C]//Proceedings of 1998 IEEE International Conference on Evolutionary Computation.Piscataway,NJ:IEEE,1998:69-73.

[9] CHATURVEDI P,DANIEL A K.Wireless sensor networks—a survey[C]//Proceedings of 5th International Conference on Recent Trends in Information Telecommunication and Computing(ITC).[S.l.]:IEEE,2014:393-422.

[10] YUN S,LEE J,CHUNG W,et al.A soft computing approach to localization in wireless sensor networks[J].Expert System with Applications,2012,36(4):7552-7561.

[11] WANG X,HE Z S.Target motion analysis in three-sensor TDOA location system[J].Information Technology Journal,2011,10(6):1150-1160．

[12] 刘洺辛,孙建利. 基于能效的WLAN 室内定位系统模型设计与实现[J].仪器仪表学报,2014,35(5):1169-1178. LIU Mingxin,SUN Jianli.Design and implementation ofWLAN indoor positioning system model based on energy efficiency[J].Chinese Journal of Scientific Instrument,2014,35(5) :1169-1178.(in Chinese)

Optimization of Wireless Sensor Network Positioning Based on PSO-BP Algorithm

BIAN Guolong1,HUANG Haisong1,WANG Anyi2,YU Kaihua3
(1.Key Laboratory of Advanced Manufacturing Technology,Ministry of Education,Guizhou University,Guiyang 550025,China;2.College of Engineering,Ocean University of China,Qingdao 266100,China；3.Weifang Power Supply Company of State Grid Shandong Electric Power Company,Weifang 261021,China)

The existing localization algorithms are discussed.For the problem that received signal strength indication(RSSI) based on the parameter model of positioning is easily affected by environment,a novel algorithm is proposed which combines particle swarm optimization(PSO) algorithm with back propagation(BP) neural network. The correction of the weight of the BP network algorithm depends on the nonlinear gradient value. It is easy to form local extremum. At the same time,the number of learning is more. It should be optimized by PSO algorithm. In order to improve the positioning accuracy,the speed constant method is used to perform filtering. Then the initial weights and thresholds of the BP neural network is optimized by the improved hybrid optimization algorithm.The performance of the algorithm is compared with that of the existing positioning algorithms. The number of hidden layer nodes varies from 12 to 19. The experimental results show that the improved hybrid optimization algorithm can significantly improve the effect of ranging error on the positioning error compared with the general weighted algorithm and the traditional BP algorithm. The minimum positioning error can reach 0.27 m in 25 m range.

wireless sensor network(WSW);localization algorithm;measurement error;back propagation(BP) neural network;particle swarm optimization(PSO);path loss model

2016-07-22；

2016-10-10 Received date:2016-07-22；Revised date：2016-10-10

贵州省科技支撑计划(黔科合GZ字[2015]3034);国家自然科学基金资助项目(51475097)；国家科技支撑计划(2014BAH05F01)；贵州省科技基金项目(黔科合J字[2015]2043);贵州省基础研究重大专项(黔科合JZ字[2014]2001)

10.3969/j.issn.1001-893x.2017.02.003

卞国龙，黄海松，王安忆，等.基于PSO-BP算法的无线传感器网络定位优化[J].电讯技术，2017,57(2):139-144.[BIAN Guolong,HUANG Haisong,WANG Anyi,et al.Optimization of wireless sensor network positioning based on PSO-BP algorithm[J].Telecommunication Engineering,2017,57(2):139-144.]

TN929.5；TP212.9

A

1001-893X(2017)02-0139-06

卞国龙(1989—)，男，山东潍坊人，硕士研究生，主要研究方向为制造物联、机械设备控制；

Email:1099205144@qq.com

黄海松(1977—)，女，贵州大方人，博士、教授、博士生导师，主要研究方向为先进制造技术、制造业信息化；

王安忆(1991—)，女，山东青岛人，硕士研究生，主要研究方向为机械电子技术；

于凯华(1991—)，男，山东潍坊人，2014年于武汉大学获学士学位，主要研究方向为电气电路工程。

*通信作者：1099205144@qq.com Corresponding author：1099205144@qq.com