明季西方高远测量仪器的引介与影响
——以《测量全义》之“小象限”为中心
潘澍原
(中国科学院自然科学史研究所,北京 100190;中国科学院大学,北京 100049)
仪器是科学活动的必要工具,也是物质文化的独特部分。文艺复兴时期,科学仪器成为欧洲社会生活中的活跃角色。明季耶稣会士利玛窦(Matteo Ricci,1552~1610)等辈梯航东来,西学随之输入,三棱镜、自鸣钟、天球仪、地球仪、日晷等西洋仪器即在最先展示与介绍之列([1],89~90,98,109~110页),并以新奇的外观和功能获得士宦权贵的关注与青睐。*科学仪器亦因此成为耶稣会士交结通关的重要手段,特别是万历二十八年末利玛窦等入京贡献,在数量有限的上贡方物中就有“自鸣钟”“玻璃镜及玻璃瓶”“映五彩玻璃石”“沙刻漏”等多种仪器([2],20页),而调试自鸣钟的需求则是他们获许留居的关键因素([1],296页)。嗣后不少士人进一步认识到西来诸器的实际功用,遂与耶稣会士合作译介其制作、用法、原理等知识,*有关案例研究,参见文献[3- 7]。高远测量仪器就是其中之一。
所谓高远测量,*“高远测量”取自康熙时期宫廷稿本《测量高远仪器用法》书名,鉴于明清之际西方数学知识译介的连续性,笔者袭用此语。该书承韩琦先生诲示得知,特此致谢。关于该书,参见文献[8],158页;[9],24页;[10],150页及同页脚注①;[11],267~270页;[12],95~105页。即高程(含高、深)、远距(含远、广、斜)等直线长度的测量(linear surveying)。其就中国古算而言即“句股”“重差”等测望之术,[13]在西方则是大地测量学(land surveyinggeodesy)和制图学的基本内容。西方高远测量知识源起甚早,希腊—罗马时期已具备某些基本方法,其后承传前绪并领受阿拉伯影响而进一步发展,成为中世纪中期学者圣维克多的休(Hugh of Saint-Victor,约1096~1141)所设实用几何中高程度量(altimetria)和平面度量(planimetria)的主要部分,*实用几何以测算现实对象几何度量的操作程序与仪器用法为主要内容,其知识传统萌发于罗马时代土地测量员(agrimensor)的工作实践,休则正式创设实用几何学,以明确区分于抽象化的理论几何学,并将其划分为高程度量、平面度量、宇宙度量(cosmimetria)三类,参见文献[14- 17]。关于欧洲中世纪中期高远测量知识所受阿拉伯影响的案例研究,参见文献[18],363~366页。及至文艺复兴时期日趋完善。除少许必要的几何理论之外,这一知识主要就是运用仪器实施测量的具体方法和实际操作,其步骤详明,推算简单,因而易于掌握,正合乎晚明社会之需。*西方水准测量、碎部测量等其他测量知识明季亦有传入,参见文献[11],254~257页。
关于明季西方高远测量仪器的引介及其反响,既有研究多集中于“矩度”,对该器的形制、用法、渊源、流播等皆有探讨。*李俨、沈康身、吴文俊曾简述明季西学著作中的高远测量知识及其仪器,参见文献[13],12~14页;[19],40~41页;[20],27~28页。冯立昇较早对明季传入的高远测量知识展开具体考察,涉及相关仪器,白欣在此基础上作出进一步梳理,参见文献[11],244~260页;[21],21~24,44~47页。关于矩度,冯锦荣考述其形制特征、西方背景及相关知识在清代的流播与研讨;黄一农揭示其作为火炮测准技术的关键仪器在明季兵书中的引介;姚妙峰就其引介的相似文本、具体来源、测量用法、本土接纳等方面展开更为细致的考察,参见文献[22],185~188页;[23],356~370页;[24],738~745,759~761页;[25];[3],37~40页;[26]。然而此类仪器并非“矩度”一种,其相互之间亦存在紧密关联。本文将首先梳理这些仪器在西方的发展脉络,再逐一考察它们在明季西学著作中的呈现,并结合具体来源分析它们的引介方式,以期对学界的现有认知稍作补正;在此基础上,着重探析《测量全义》所载“小象限”的仪器属性、制作原理和西方渊源,进而讨论其可能的传播与影响,及其被本土知识接纳并相与融合的具体方式。
1 西方高远测量仪器的主要类别及其源流
1.1 西方高远测量仪器的两大类别
按照所需量取对象和相应推算方法,西方高远测量仪器大要可分为两类。
一类仪器用以量取角度,而以平面三角形解法作相应推算。测量高远时,先令仪器与目标参望相准,而就所成视线和所知、所求线段构造平面三角形,再量取形内角度,结合已知边长,即可利用三角函数线段长度*迄至17世纪前期,三角函数普遍采用与设定半径长度相应的诸线段长度表示。推算所求边长:或于直角三角形内采用正、余弦或正、余切等适当线段,或于一般三角形内应用对边与对角正弦成定比的正弦定理。
此类仪器以象限仪(quadrant,拉丁名quadrans,一名四分仪)为典型。它原本用作天体地平高度(角)的观测,亦即地平垂面的角度测量,后来则发展出更多功能,分化为数种类型,在天文、计时、航海、测量等领域均有应用。[27- 28]其形制设计可追溯至希腊化时期天文学名家托勒密(Ptolemy,约100~约170)的描述,具体实物则在中世纪由阿拉伯人自星盘发展而来——取星盘四分之一并放大尺度,以便标示更为清晰而细密的弧度划分,传入欧洲后见诸斐波那契(Fibonacci,即Leonardo of Pisa,约1170~1240以后)等人的著作(图1),*斐波那契最先在欧洲绍述象限仪,其仪器形制见文献[29],204~206页。并随三角测量(triangulation)方法的普及成为欧洲大地测量所用的主要仪器(图2)([30],77~83,165~168页)。其弧心或安窥衡(alidade,sighting rule),或系权线(plumb-line),窥衡或仪身直边之上相应设置两个窥表(sight,亦称照准器)。使用时,或仪身不动,转动窥衡以准望并读数;或转动器身,用其直边准望而以权线读数。象限仪可直接量取锐角或校正直角,至于钝角则需通过其余角间接处理,为便于操作,形制增倍的半圆仪和全圆仪也在文艺复兴时期陆续出现。

图1 斐波那契向欧洲介绍的象限仪图示([29],204页)
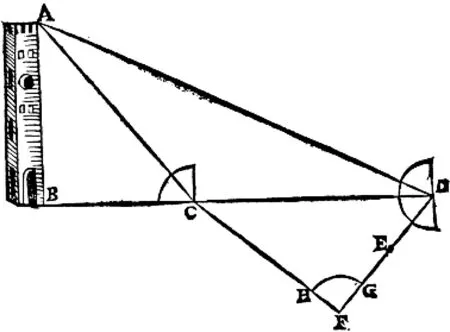
图2 西方著作所示用象限仪测量高远([31], De Dimetiendi…,fol.33v)
另一类仪器的直接量取对象或间接处理对象为长度,并以长度比例关系作相应推算。测量高远时,亦以之参望目标,而就所成视线和所知、所求线段构造平面直角三角形,同时构造相似的小三角形,再量取小形之上的某边长度(实际长度或比例长度,详后),结合两形已知边长,即可通过相似比例推算所求边长。
由定长直杆做成的表(staff,拉丁名baculus)是此类仪器的代表。作为西方最为古老而简易的测量仪器,表起初用于竖立地面成影以确定时日,故也称影表(shadow staffgnomon)。希腊—罗马时期,表已普遍用作高远测量([30],38~39页;[32],24~26页),其后一直作为基本仪器承继沿用。依据同一时刻物体高度与其日影长度的确定比值,已知表高,量取表影、物影,即推得物高。进而以表端、物端参望,构造相似三角形的对边比例关系,其视线如光线,目与表、物之间距亦如表影、物影,由此可在竖直平面内知远求高、知高求远;高、远俱不知时,则用两次测量以距差推求。至于地平测远,亦构造相似三角形为法,唯需以四表参望。

图3 西方著作所示用平面镜测高与用矩尺测高([33],fol.15v;[34],40页)
平面镜(拉丁名speculum)和矩尺(拉丁名normagnomon)亦属此类。两者原非测量高远的专门仪器,而是借作此用的简易工具(图3)。利用前者的光学特性和后者的几何特征参望目标,容易在竖直平面内构造出适合求解的相似直角三角形。*平面镜测量用法及其收载著作参见文献[30],284~285,315~316页;矩尺测量用法及其收载著作参见同书289,310~311页。
1.2 分度测量仪器:一类基于长度比例关系推算的高远测量仪器
以上所举第二类高远测量仪器表、矩尺、平面镜等,形制均较为简单,其本身仅能构造相似形,如目与表、人与镜、矩边射地点与矩角垂地点等相距长度,则需由尺、绳等另行量取。同属此类的分度测量仪器则操作便宜,它的出现正是表的测量功用渐续演进的结果。为直接量取表影长度或表目间距,乃引入与竖表垂直连接的横表,由此构成组合表(staff combination)。在其初始形式中,两表固定相接,表端至交接点长度恒定,测量者必须携之前后移动直至特定位置,方能使两表表端与目标点参望相准。就此缺陷,又演生出两种等价的改进方式:
a. 活动调节一表位置,至两表表端与目标点相准,记取另一表的伸出长度;
b. 一表表端连接斜杆,旋转至某处与目标点相准,记取另一表的被截长度。
如此,可在任意位置将实际高远等所求线段以相同比例转换到尺度较小的仪器之上,转换后的相应长度亦可由仪器本身直接量取读数([30],39,63页)。为进一步简化计算,又将横、竖两表实际长度作每分相等的均匀划分并刻画标度和相应数值,由此成为量取分度亦即比例长度的高远测量仪器,上述两种改进亦逐步形成此类仪器的两种典型代表,即十字杆(cross-staff)与几何矩(geometric square)。
(1)十字杆:纵横游移读取分度
十字杆,亦称雅各布杆(Jacob’s staff,拉丁名baculus Jacobi)或测量杆(拉丁名baculus mensorius),其主体一般由一支较长的主干(main staff)和一支较短的衡杆(crosspiecevane)垂直交接组成,短衡沿主干方向前后游移,通过衡杆上固定或移动的窥表准望,即可由主干的角度标度量取物体自身或两物之间的距度(即视角距,angle of sight),亦或量取物体的地平高度,或由主干的分度标度测算物体的高远距离(如图4测量广度)。其最初样式系由法国数学家、天文学家热尔松(Levi ben Gerson,1288~1344)发明,经若翰王山即著名德裔天文学家、数学家雷吉奥蒙塔努斯(Regiomontanus,本名Johannes Müller von Königsberg,1436~1476)的简化,*关于若翰王山的科学史迹,参见文献[35-36]。除天文学、数学的丰硕成果外,王山氏在科学仪器的发明、制作方面也十分活跃。他在匈牙利王国期间曾创制一种黄赤转换仪(torquetum),制作托勒密尺(regula Ptolemaei)即三角仪(triquetum)并论述其高远测量用法,后更在当时欧洲的金属加工与仪器制作中心之一纽伦堡设立专门作坊,制造十字杆、三角仪、浑天仪、日晷、星盘等,而这些仪器对其天文观测和历法编制助益良多,参见文献[36],98~100,135~140页;[5],17~19页。又,其人汉名以往学者作“玉山若干(若干玉山)”“玉山王干”([37];[38],154~155页)。2015年4月韩琦先生向笔者指出,“regiomontanus”内含“国王”与“山”之意,“玉山”当是“王山”之讹;笔者据此核查《崇祯历书》原刻本,其《月离历指》所及三处分作“王山玉幹”“玉(王)山玉幹”“若翰王山”([39],卷3,24b页,27b页;同书卷4,28b页),《西洋新法历书》本亦同,先生所见甚是,而“若翰”即Johannes之音译。又查得《古今图书集成》所收《月离历指》相应三处讹作“玉山王幹”“玉山王幹”“若幹玉山”([40],历象汇编·历法典,卷57,30册28b,29a页;卷58,30册34b页),前辈讹误或最初由此引出。广泛运用于天文、航海、大地等各类测量活动,成为文艺复兴时期欧洲最为流行的科学仪器之一([30],83~87,194~206页;[41])。

图4 西方著作所示十字杆及用其测广([33],fol.7v, 8v)
(2)几何矩:旋转游动读取分度
几何矩*该译名承用自冯锦荣,参见文献[22],187页;[25],151页。拉丁名quadratum geometricum,意为几何的方矩,“方矩”是其外形,而“几何的”在此具体指其用作测量。*quadratum与英文square同义,可专指正方形,亦可指矩尺(carpenter’s square)、三角板(set square)等以矩边为特征的图形,该仪器外形虽呈正方,但核心部分是两边标示分度的矩尺形。geometricum直译“几何的”,在此名中则用其原义“土地测量的”,安国风曾指出这一具体意涵,参见文献[42],298页。它初由阿拉伯学者创制,不久即引进欧洲,收入早期实用几何著作,*欧洲最早述及几何矩的著作系《无名氏几何学》(Geometria incerti auctoris)([43],330页)。该篇早先被归入热贝尔(Gerbert d’Aurillac, 约946~1003)名下,后续研究表明其著作年代应稍早于热氏。奥地利天文学家普尔巴赫(Georg Peurbach,1423~1461)加以改进并撰作专书解说[44](图5)以后逐渐流行([30],75~77页),*普尔巴赫将几何矩用作天文角度的精确观测,其角度值通过分度测量和正弦表间接获得,参见文献[30],77,150~151页;[36],26~27页。普氏天文学研究出众,对相关仪器亦述论甚多,参见文献[36],17~30页;[45]。值得指出的是,普氏的黄赤交角观测记录曾载入《崇祯历书》,译名作“褒尔罢”,参见文献[38],179页。普氏亦是前揭若翰王山的亲密师友,他们接续完成的《托勒密至大论概要》(Epytoma…in Almagestum Ptolomei,1496)是文艺复兴时期最重要的《至大论》译本,利玛窦曾携其书入华并作校算笔记,译撰《乾坤体义》之际甚或参考及此,后《崇祯历书》介绍的某些托勒密理论也可能据该书编写,所称“王宝翰”者当即二人其一,参见文献[46],26~27页间插图;[47],363~367页;[48],104,137页;[49],311~312页。学者著述多有推介,如意大利著名数学家、机械学家塔塔利亚(Niccolò Tartaglia,1499~1557)就曾在《新科学》(NovaScientia,1537)中详述其略作改造的仪器形制及多种测量用法。[50]*关于塔塔利亚的具体述论及该书后续版本的相关增补,参见文献[51],23- 29页。吴文俊曾据文献[52]认为几何矩系塔塔利亚为炮兵发射炮弹而设计([20],27,28页),然该器并非塔氏原创。
几何矩主体为一正方形框或板,以一角为枢纽(pivot),两对边作相同分度的均匀划分及其细分,经典分法以12分或24分、60分等较为多见,后期则有10分及100至1000小分等十进分法;再从两边各分点向枢纽牵引一段放射状直线,由此形成两条标示分度的垂直等长直边,称作直影(right shadow,拉丁名umbra rectaumbra extensa)和倒影(contrary shadow,拉丁名umbra versaumbra conversaumbra deiecta),意即竖表(直表)与横表(倒表)之影。与象限仪类似,几何矩也有使用窥衡或权线的两种类型([30],75~76页),测量时以窥衡或枢纽邻边之上的窥表与目标点参望相准,窥衡或权线所指直、倒影分度比全表分度即实际高远相比。如测量塔顶高度(图6),塔高(FG)与前距(GH)之比,即全表(12分度)与所得直影(3分度)之比;而塔高与后距(IH)之比,则为所得倒影(10分度)与全表(12分度)之比。*此例选自文献[53],24- 25页。

图5 普尔巴赫设计的几何矩图示([44],封面)
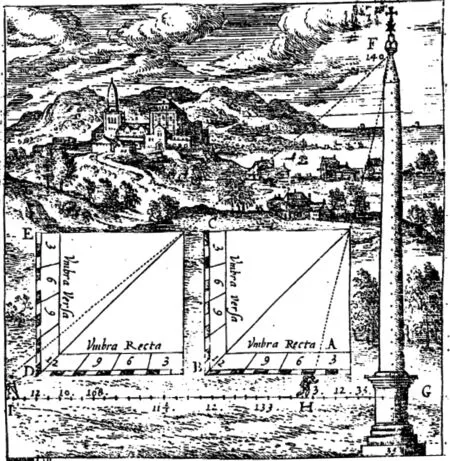
图6 以几何矩测量塔高([53],24页)
(3)影矩:同于几何矩的仪器组件
作为几何矩的核心部分,由直影和倒影两边构成的纵横等长且均匀标示分度的矩尺形即所谓的影矩(shadow square)*该名冯锦荣曾译作“日影正方形”“日影测定正方形”([22],187页;[54],183~184页;[23],356页;[25],155页)。因该仪器组件呈矩尺形,今据以改译为“影矩”,亦与“几何矩”的译法保持一致。,在欧洲实用几何传统上也被称为测高标尺(scala altimetra)*该名可见文献[53],3页;[55],93~94页边注;下文所示星盘实物(图7)。该名与圣维克多的休所设实用数学分类的关联承Jens Høyrup教授指示,笔者由此进一步展开考察,受益尤多,特此致谢。。在几何矩出现以前,影矩已作为测量高远的功能组件附载于其他仪器之上,几何矩则是由其实体化而成的独立仪器([30],68~70,75页)。
影矩最初当系波斯数学家、天文学家花拉子米(al-Khwārizmī,约780~约850年)在星盘仪母(mater)背面引入,*目前已知最早述及星盘影矩构造和用法的阿拉伯著作及其现代译注,参见文献[56],特别是139,141~145,165~166,170~171页。其中,涉及影矩构造的文本是否为花拉子米所作尚无确论。旧说认为首述影矩者系阿拉伯天文学家、数学家巴塔尼(al-Battānī,约858~929),参见文献[30],68页。后传至欧洲,*最早述及以星盘影矩测量高远的欧洲文献亦即前揭《无名氏几何学》([43],317~322页),文艺复兴时期的经典样式是分别刻画于仪背下部两象限中对称相接的两个影矩(图7),下边横者为直影,两边竖者为倒影。西式星盘的影矩分法亦如后来的几何矩多用12分或其倍数,而阿拉伯传统的东式星盘的影矩则往往同时设置12分度与7分度两种(图8)。*关于东式星盘与西式新盘的构造特征,参见文献[57],19~20页。另外,也有局限于某象限内的单影矩(图9、图10)或扩展至全象限的四影矩(图11),圣维克多的休还曾描述下部和右上象限三个影矩的样式(图12)([14],194,197页)。源自星盘的象限仪也往往在弧内设置影矩(图1、图13),而几何矩流行后也有在其内设置象限弧亦即影矩在象限弧外的相反形制(图14)出现([30],79,152,167~168页),这种角度与分度测量兼用的组合仪器,亦称作几何象限仪(geometric quadrant,拉丁名quadrans geometricus)([28],42页)。*文献[28]将“几何象限仪”与“几何矩”视为同一仪器的不同名称,冯锦荣曾对此予以沿用([22],187页;[25],140~141页)。笔者倾向于认为任何象限仪都必须包含四分之一圆弧,几何象限仪只是在普通象限仪或内或外加置影矩而已,几何矩则是影矩的独立仪器形态,两者仍有一定区别,如费恩(Oronce Finè, 1494~1555)同一部著作内既有独立仪器形态的几何矩,也有弧内附设影矩的几何象限仪(图13)([33],fol.3r,6r)。又,安大玉曾将“矩度”(即几何矩,详后)对应于西方的“四分仪”“幾何測量用の象限儀”“幾何象限儀”“幾何学的象限儀”([58],312页;[59],138~140,146~147页),乃是将quadratum误认作quadrantum(quadrans的属格形式)所致,与上述两名及其区分无关。附设影矩组件的星盘和象限仪同样具备基于长度比例关系推算的高远测量功能,而不必再另行制备和携带几何矩,因而在文艺复兴时期广泛使用(图15、图16)。此外,影矩还以各种样式设置于16~17世纪出现的多种新型测量仪器之上,足见其流行普及情势([30],180~194页;[28],43~45页)。*该星盘约1500年意大利制,牛津大学科学史物馆藏,藏品号35146。其影矩内标刻名称Scala Altimetra。图像截取自:http:www.mhs.ox.ac.ukastrolabecatalogueimageReportAstrolabe_ID=246.html*该星盘伊斯兰历996年(15878)波斯制,牛津大学科学史物馆藏,藏品号52399。图像截取自:http:www.mhs.ox.ac.ukastrolabecataloguebackReportAstrolabe_ID=170.html*该星盘1558年萨拉戈萨(Zaragosa)制,牛津大学科学史物馆藏,藏品号48892。图像截取自:http:www.mhs.ox.ac.ukastrolabecatalogueimageReportAstrolabe_ID=233.html*该星盘约9世纪晚期叙利亚制,牛津大学科学史物馆藏,藏品号47632。图像截取自:http:www.mhs.ox.ac.ukastrolabecatalogueimageReportAstrolabe_ID=131.html*该星盘约1600年巴黎制,牛津大学科学史物馆藏,藏品号35082。图像截取自:http:www.mhs.ox.ac.ukastrolabecatalogueimageReportAstrolabe_ID=245.html
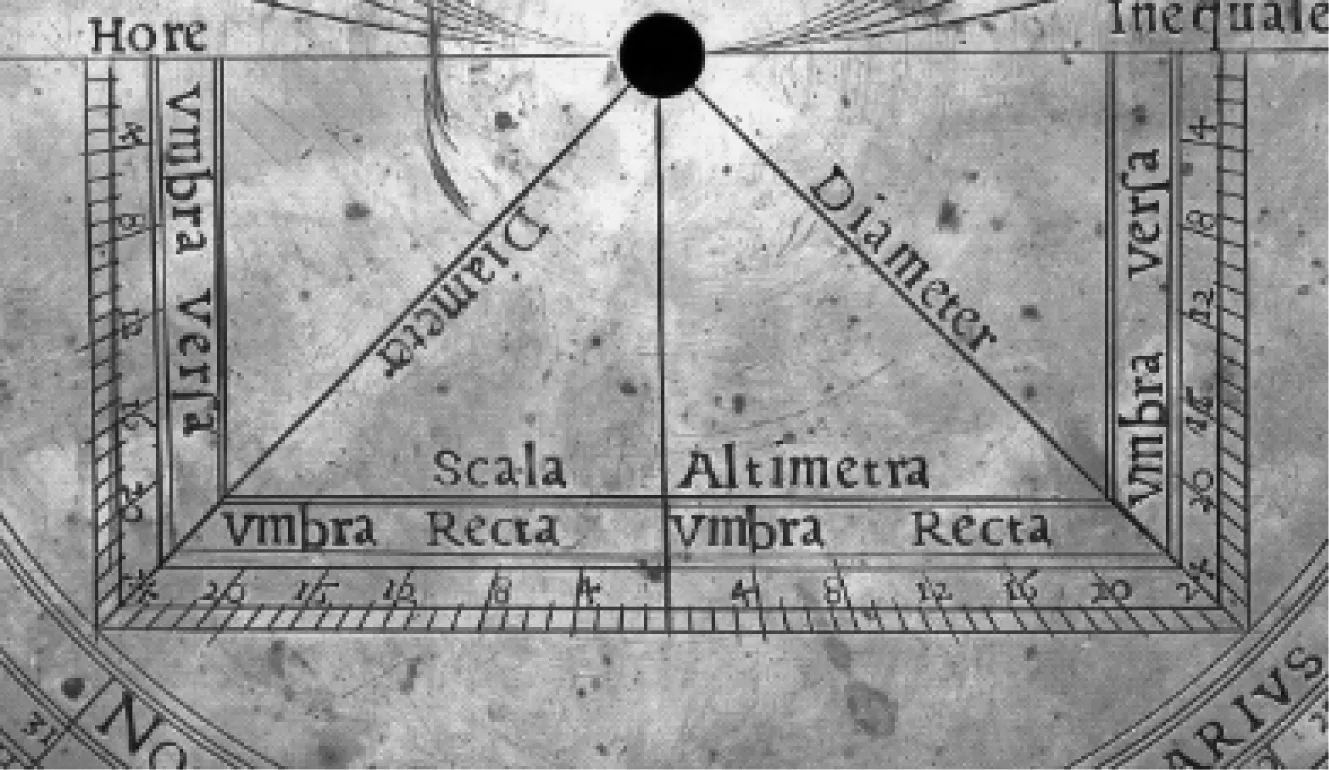
图7 西式星盘仪背下部24分度双影矩②

图8 东式星盘仪背下部左12分度右7分度双影矩③

图9 西式星盘仪背左上象限单影矩④

图10 东式星盘仪背左下象限单影矩⑤

图11 西式星盘仪背全象限四影矩⑥

图12 圣维克多的休设计的 星盘的三影矩([14],197页)

图13 西方著作所示内设影矩的几何象限仪([33],fol.6r)

图14 西方著作所示外设影矩的几何象限仪([53],3页)

图15 西方著作所示用星盘影矩测高处物高([60],fol.75)
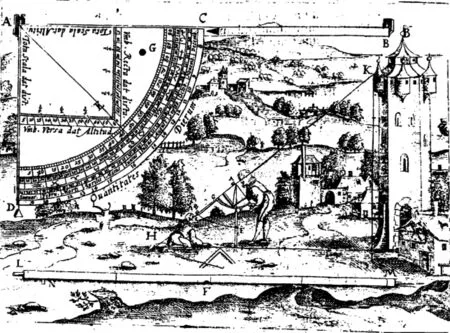
图16 西方著作所示用象限仪影矩测高([53],41页)
2 明季西方高远测量仪器的引介
西方高远测量仪器及其使用方法、原理等知识在明季的引进与介绍,*本段仅按时序简述相关史迹,具体考证参见笔者博士学位论文([12],41~45页),详细阐论另文发表。始于耶稣会入华早期。万历十七年(1589)利玛窦出离肇庆迁居韶州之初,就曾向韶州同知刘承范等人演示“测地”“测山川河海”之器,并用其测算光孝寺到皇冈山山顶的距离([61],5页)。为宣扬西学的知识优势以促进传教,利玛窦等耶稣会士每每介绍高远测量仪器,引起中国士人的浓厚兴趣,相关著述陆续问世。其一是李之藻(1565~1630)就其从利氏所学“通宪平仪”即星盘(planispheric astrolabe)原理、用法演撰的《浑盖通宪图说》(1607),该书末节“句股测望图说”([62],下卷,42a~50a页)即简述利用包括星盘组件影矩在内的多种仪器的高远测量方法([58],311~312页;[59],235~236页)。其二是利玛窦、徐光启(1562~1633)合作译撰的《测量法义》(约1610)[63],这部西方测量专论对基于长度比例关系推算高远的仪器、方法和原理均有阐述,所附《测量异同》则以“旧篇”与“今译”“对题胪列,推求异同”([64],1a页)。*其后李之藻编纂实用算术著作《同文算指》(1614),亦将《测量法义》《测量异同》的内容稍加简易而命作“测量三率法”([65],1a~11b页)收入,参见文献[66],10~11页。《浑盖通宪图说》测量部分和《测量法义》的解法、用例多相近同([26],8~10,68~69页),最初可能皆是据利玛窦在罗马学院(Collegium Romanum)研修期间(1572~1577)习得的知识分别编译成稿,*安国风(Peter M. Engelfriet)首先提出这种推断,认为后者编自利氏携至中国的课程笔记的可能性最大,参见文献[42],297页。关于此推断的进一步论证,参见文献[12],44页。后期修订时又或就利氏业师丁先生即耶稣会数学家克拉维乌斯(Christoph Clavius,1538~1612)所著《实用几何》(GeometriaePracticae,1604)卷3“使用几何矩的直线测量(Earundem linearum rectarum dimensionem per Quadratum Geometricum exequens)”([55],92~173页)有所参考。*因论题方法对应明确,学界一般将丁氏《实用几何》直接视为《测量法义》和《浑盖通宪图说》测量部分的底本,参见文献[67];[59],138~140页;[68],44页。新近研究表明,丁著论题多无具体算例,矩度形制相较《测量法义》亦有重要细节差异,参见文献[26],11~13页。其三,崇祯初年明廷开局修历之际,耶稣会士罗雅谷(Giacomo Rho,1593~1638)、汤若望(Johann Adam Schall von Bell,1592~1630)与徐光启、李之藻等人译撰的《测量全义》(1630~1631)对西方实用几何知识作出全面介绍,*《测量全义》属《崇祯历书》法原部,崇祯三年(1630)九月译成2卷,“系臣光启、臣之藻同陪臣罗雅谷译撰”;四年(1631)八月10卷编完进呈([69],346~349,385~386页)。该书各卷分述“测直线三角形”“测线”“测面”“测体”“测曲线三角形”“测球上大圈”“测星”“仪器图说”等([70],测量全义叙目,6a~b页),正是当时欧洲实用几何知识分类的体现。是书原刻本目前仅知两部残卷存世,藏法国国家图书馆和韩国首尔大学奎章阁。本文所涉该书内容,一般引用顺治二年(1665)《西洋新法历书》之重修本即文献[70],仅第三卷仪器相关内容引用《崇祯历书》之原刻本即文献[71]。其第2卷“测线上”摘译自意大利数学家、制图学家玛金尼(Giovanni Antonio Magini,1555~1617)的《论用象限仪与几何矩的测量方法》(DeDimetiendiRationeperQuadrantem, &GeometricumQuadratum)前3卷,*白尚恕曾考证《测量全义》第1卷和第2卷主要摘译自“《平面三角测量》(De Plani Triangulis, 1604)”“前部第四、五章”和“后部前三卷”([72],143,147页)。今查原书即文献[31],内含《论平面三角》(De Planis Triangulis)一卷与《论用象限仪与几何矩的测量方法》(De Dimetiendi Ratione per Quadrantem, & Geometricum Quadratum)五卷两种,即白氏所谓前、后部分,今用二者原名。兼述以平面三角形解法和长度比例关系推算为基础的高远测量知识,第3卷“测线下”则以数题增补,并附说仪器制作和使用。
以下分别就前揭各类各种西方高远测量仪器,列叙明季西学著述的相应介绍与论说。
(1)象限仪*明季西学著作介绍的天文测量仪器星盘和碎部测量仪器全圆仪亦有角度量取功能([62],上卷,2b,4a页;[73],2b页;[71],34b页),自然也可用于高远测量,但原书既未说明,今亦不予列论。
象限仪自耶稣会士入华早期便有携入、制作和展示([1],161,244,246页),但直至崇祯年间译撰《测量全义》时才得以图文解说的形式展开详细绍述,用以测量高远者则在该书第3卷。*该书第10卷所述“新法测高仪”六式中的“象限悬仪”“象限立运仪”“象限大仪”([70],卷10,29a,31a,31b页)均为天文观测所用,系自第谷(Tycho Brahe,1546~1601)著作译撰,参见文献[72],158~159页;[54],183~187页;[5],126~127页。又,最先对象限仪及其天体地平高度测量功能予以粗略图文介绍的汉文著作是1593年在菲律宾出版的《辩正教真传实录》,参见文献[25],138~139页。其“造象限仪法”依次解说仪身和窥衡制作,其中指明象限弧上标度自两端“皆可起算,互用之”,而窥衡亦可作两支,“同心同线,可定可移”([71],6a~7b页),透露出译撰者注重实际操作便利的用意。“用象限法”则给出该仪利用窥衡与权线读数的操作指南,而就其仪身位置分别称作“定仪”与“游仪”,并解释两者“其理同也”([71],7b~9a页)(图17)。这一兼顾两类的用法说明十分重要,因为在竖直平面内窥望高深时,定、游模式可任作选择;但若沿地平或斜坡安置仪器,权线无法指示标度,而只能使用窥衡。事实上,《测量法义》第2卷所有论题统一采用窥衡定仪的方式叙述象限仪的高远测量方法及具体步骤(如图18)。

图17 《测量全义》所示高远测量象限仪利用窥衡和权线读数([71],7b,8a,8b页)

图18 《测量全义》所示以窥衡象限仪平面测远(左)和望高测远(右)([70],卷2,1a页,17b页)
(2)表及平面镜、矩尺
《浑盖通宪图说》《测量法义》皆设立表因远测高、因高测远、因远测极远诸题,实与前揭丁先生《实用几何》卷3用表测量的部分论题相应([59],140页;[26],68页)。这些内容显然与中国传统立表测望的仪器、方法、理论等极为近似,*吴文俊曾就此认为明季西学著作相关论题的解法乃至所用仪器系利玛窦袭取自中国传统算术([20],27~28页),丁氏《实用几何》等西方著作所述诸题足证其论未允。然吴氏观点实际蕴含古代世界知识交流的问题意识,即当时西方高远测量知识本身在此前历史上曾否受到中国古算同类知识特别是“重差”的影响,而后者又如何辗转西传等等,仍待深入讨论,参见文献[18]。李之藻、徐光启在译介时径以“表”名其器,乃是合乎情理的自然之举。而通过两相比较,徐氏亦在《测量异同》中指明用表测量的传统中法与新译西法相同([64],1b,2b,4a页)。
平面镜和矩尺亦为《浑盖通宪图说》《测量法义》所载述,前者用以测高,后者用以测远([62],下卷,46a,49b~50a页;[63],17a~b,20b页)(图19),较丁氏著述所论不同情形([55],160~163,153~154页)(图20)为简。《测量全义》第3卷“增题二”“矩尺测量法”则有测高、测远、测深三种([71],3b~4a页)(图21)。
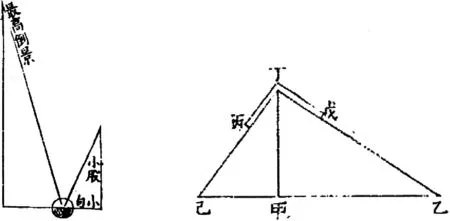
图19 《浑盖通宪图说》《测量法义》所示用用矩尺测远和平面镜测高([62],下卷,46a页;[63],20b页)

图20 丁氏《实用几何》所示用单、双平面镜测高与用矩尺测远、测高([55],160,162,154页)

图21 《测量全义》所示用矩尺测高、测远、测深([71],3a,3b,4a页)
(3)“古弧矢仪”与横竖游移“方木表”:十字杆及其测量高远的简易形制
明季引入的西方高远测量仪器以直接量取分度者为最大一端。*中国古代观测天体位置的浑仪即是分度测量仪器,其直接量取对象是各圈环分度即均分设定圆周所得的比例长度,以其测天的实质是同心圆周上对应弧长的同比例放大,参见文献[74];[75],95~104页。其中,十字杆的介绍见于《测量全义》第10卷“仪器图说”,计有“古弧矢仪”“弧矢新仪”“弩仪”三种([70],卷10,13a~19b,34b~37a,37a~b页),所言形制、用法甚详。*此三种不同样式十字杆的简要分析,参见文献[5],116~120页。本文仅对与高远测量有关的“古弧矢仪”稍作述论,三仪的形制特点、技术细节及其西方背景和具体来源将另文探讨,此不赘论。其“古弧矢仪”(图22)作法曰:
仪有七物,干一,衡一,管一,窥表四。……衡之长,当干之长二十分之九。……干与衡各先为一管,……干管置下,衡管置上,各以其一端纵横相切,镕金合之。干管之上端加窥表一,横之两端各定置一窥表,别作一游表加于衡,可离可合,转移用之。两管之旁各作螺柱,每移管至其所欲至,则旋螺而止之。([70],卷10,14a~b页)
从中可见此仪长干、短衡垂直交接且可活动调节等诸特征,正与十字杆相合。其后“分法”,所称“横之一面二百平分之,用元度以加于干之同方面,四百平分之”([70],卷10,14b页),即以相同分度均分干与衡。又后“用法”,起首即谓“此仪之用有二,一以测日月星之高度、距度,历学所用;一以测高深广远,地学所用”,而注称“测地法,略见第三卷增题”([70],卷10,15b页)。*同篇又称“此仪于地学中,用测高深广远,为径捷法”([70],卷10,18b页)。查考同书第3卷“增题四”“量高远深”所用之器(图23):
用方木表,承以鼎足之跗,垂权取直。表端以下一尺或五寸,用一十或一百平分之,下作方孔,长寸许、广三分,贯以横表,游移无定,亦以十或百平分之,纵横作直角。
欲以测高,则“丙上立表,横表游移,令丁、戊、乙为直线”,得“丁己若干分与己戊一百分若丁庚与乙庚”([71],5a页)。依此判断,其横表乃是横向左右游移,相当于古弧矢仪的主干,而保持固定的竖表则如其短衡。此器又可“用重表”作前后两次测量以“无高求远”(图24,西方著作同类论题如图25),而在“高上测高,用重表再测”即高低两次测量的情形中,则需“定表横用,游表直用”([71],5b页)。这种可活动调节的横竖组合表,依据两表表身之上均匀标示的分度进行比例测算,可视为十字杆用作高远测量的一种简易形制。

图22 《测量全义》所示古弧矢仪([70],卷10,13a页)
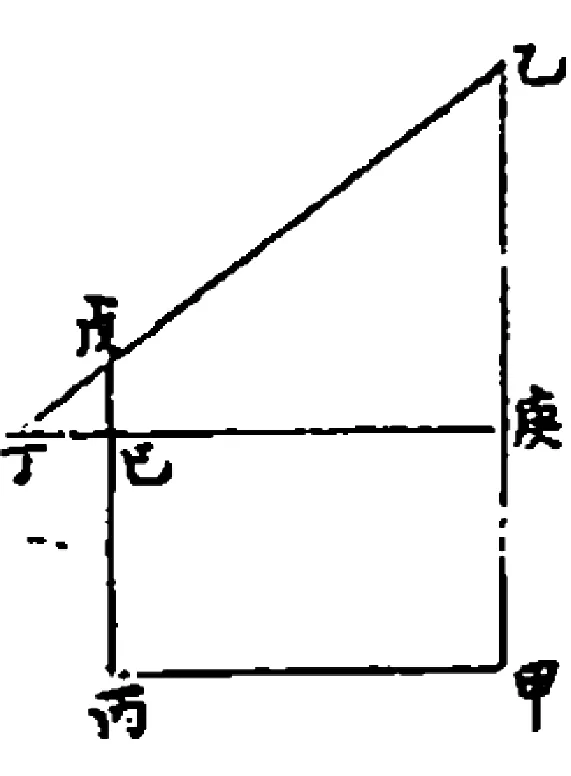
图23 《测量全义》所示横竖游移组合表及其测高([71],5a页)

图24 《测量全义》所示用横竖游移组合表重表无高求远([71],5b页)

图25 西方著作所示用十字杆两次测量推求楼高([76],fol.30v.)
(4)“矩度”:几何矩
几何矩是明季西学著作绍述最多的高远测量仪器,《测量法义》《测量全义》两部测量专书先后皆有详论,而名曰“矩度”。此名早在万历三十一年(1603)徐光启向上海知县刘一爌呈送简明技术报告《量算河工及测验地势法》时即已行用,*该文原载《农政全书》,题名“玄扈先生量算河工及测验地势法”,题下注“万历癸卯送上海刘邑候”([77],18a页)。王重民最早注意此篇,将之收入徐氏文集,并强调其研究价值,参见文献[69],57~62页;[78]。“上海刘邑候”即刘一爌,任上曾建龙华港闸,徐氏该篇或为此作,参见文献[69],62页;[79]。篇中如“用矩度对准人足或记处,看在直景何度何分,用地平测远法算得河面阔处”([77],19a页;[69],58页)等内容与《测量法义》论题多有相关,当是万历二十八年(1600)徐氏在南京初会利玛窦之际所获,*冯立昇首先指出该篇包含矩度及其测量方法等西方知识来源,后冯锦荣推断徐光启约自南京结识利玛窦起习得“西方普通测量学”要旨,姚妙峰指明篇中某些方法与《测量法义》论题的关联,但前两者将篇中多数方法归于中国传统测量,后者亦将“重矩、重表勾股量高法”与《测量异同》第6题所述旧法对应,恐非允当,参见文献[11],211~213,235页;[23],356页;[24],738~739页;[26],21页。“矩度”之译应出自其手笔。
《测量法义》首节“造器”(图26)正式介绍几何矩的制作方法:
用坚木版或铜版,作甲乙丙丁直角方形。以甲角为矩极,作甲丙对角线。次依乙丙、丙丁两边各作相近两平行线。次以乙丙、丙丁两边各任若干平分之,从甲向各分各作虚直线,而两边之各外两平行线间则作实线,如上图,即外两线间为宗矩极之十二平分度也;其各内两平行线间,则于三、六、九度亦作实线,以便别识。([63],1b~2a页)
所谓“矩极”即枢纽,“外两平行线”间实线即直影、倒影标度。又有设“通光窍”之窥表,用以“审定度分”之权线([63],2a页)。次节“论景”,论说直、倒二影的来源,*介绍西方圭表测影的《表度说》对直影、倒影的基本原理亦有详细解说([80],12a~15a页)。又,《测量全义》“圭表仪”称直影为“正景”([70],卷10,48b页)。并指明矩度“傍通光耳之分度边为直景,而对通光耳之分度边为倒景”([63],5b~6a页)。这些述论与丁先生《实用几何》“几何矩的构造(Quadrati Geometrici constructio)”([55],93~96页)(图27)一节内容大致相同,唯两处存在细节差异*此两处差异均系姚妙峰首先指出,参见文献[26],12页。:丁氏已将影边改作10分,*“ANTE PONO autem diuisioni consuetae in 12.vel 720.vel 1200.partes diuisionem nostram in partes 10. vel 100. vel 1000. aequales, propterea quod, si instrumentum propter paruitatem sectum sit tantummodo in 10.”([55],94页)而《测量法义》则仍用传统的12分;丁书图示形制兼有权线和窥衡,即所谓“垂悬矩与固定矩”(quadratum pendulum, ac stabile)([55],94页),而《测量法义》仅介绍前者,也就将仪器使用范围限制在垂直平面内。
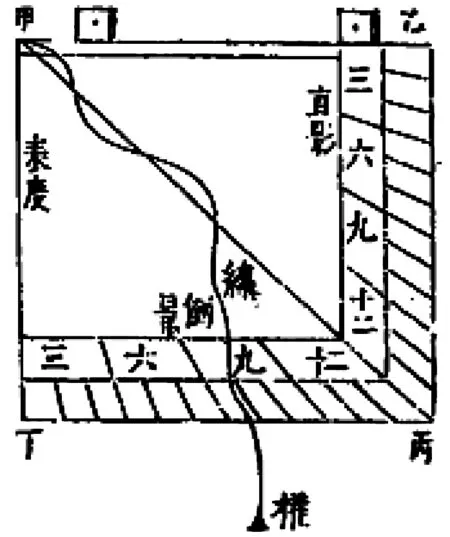
图26 《测量法义》所示矩度([63],1b页)

图27 丁氏《实用几何》所示几何矩([55],93页)
《测量全义》在主要介绍使用象限仪的高远测量方法以外,也述及几何矩用法,所论“用矩度者,以器上小形,当所测大形也”([70],卷2,4b页),可谓其测量原理的精要概括。第3卷“造矩度法”称“角止作心,加窥衡、加权线任用”,一体说明两种仪器类型,而“定仪于立边书高深,平边书远;游仪于表旁边书远,对边书高深”,即分说两者的直、倒二影位置,盖以“远”为直影,“高深”为倒影。为兼顾地平远距测量,书中着重介绍窥衡式矩度(图28),其“各边作一百分,每对边分以直线相联成网目形”([71],9a~b页)。这一非典型形制亦在西方渊源有自,如西尔维奥·贝利(Silvio Belli,约1520~约1579)的几何矩设计[81](图29)就与之近同。*贝利的几何矩主体正方板各边分作30分,对边每5分度相连成网状,参见文献[30],154页。
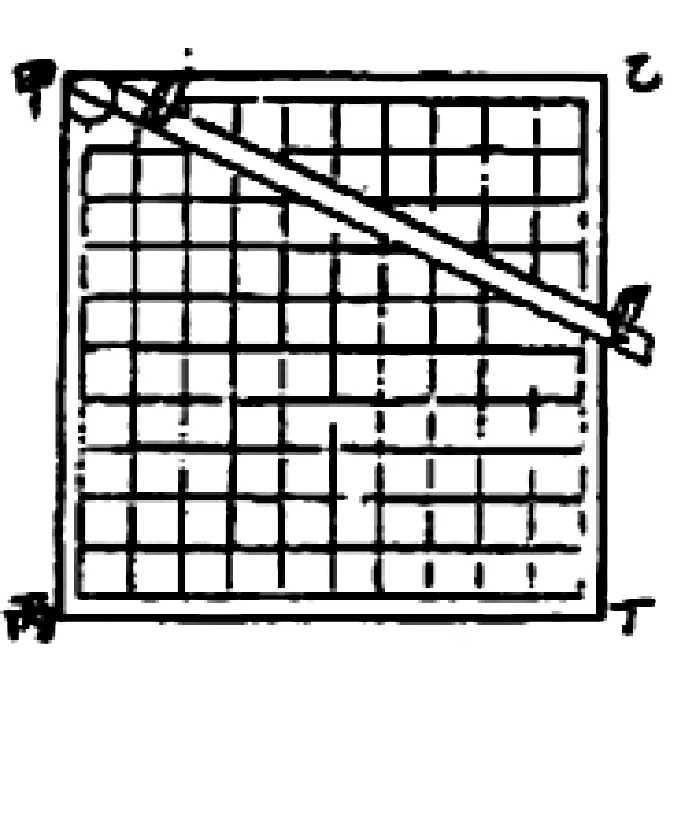
图28 《测量全义》所示窥衡矩度([71],9a页)
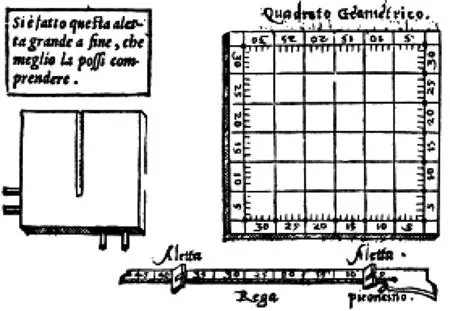
图29 贝利的固定几何矩设计([81],5页)
(5)“方仪”与“矩度”约法:星盘与象限仪上的影矩
由于使用便利,作为仪器组件的影矩也在明季引介入华。《浑盖通宪图说》专论星盘,述及双影矩形制和用法,上卷“总图说”的“仪之阴”即仪背部分谓中央“下截方仪以句股测远近高深”([62],上卷,3b页),下卷“句股弦度图说”更详说其制(图30):
法:取仪背地平线下半规为半方形,两角对枢心各作一斜线曰弦,以为句、股相交之限,在下者曰句,在侧者曰股。以望高若深为大股率,取仪小股准之,以望远若近为大句率,取仪小句准之,皆据瞡筩以定其度。凡二股、二弦、一句,其句匀分二十四度,其两股各匀分十二度,而每度之中又各匀为十二分,每停共一百四十四分。如不能细分,则刻作三分或五分、七分,举其大略亦可,但每画皆宗枢极。凡有所测,以筩对影,而审察其度云。([62],下卷,24a~b页)
比照该书底本丁氏《论星盘》(Astrolabium)的相应部分,其半方形的“方仪”即影矩(scala altimetra),而“瞡筩”即可于盘心旋转、指示读数的窥衡 (mediclinium)。[82]横在下端的直影与竖于两侧的倒影则分别以传统算学的句、股命之,其书李氏自序所谓“间亦出其鄙谫会通一二,以尊中历”([62],浑盖通宪图说自序,4b页)的编撰旨趣由此可见一斑。*李之藻将《测量法义》的矩度介绍收入《同文算指》之际,在沿用译名“直景”“倒景”的同时,也将其另称作“句景”“股景”([65],2a页),参见文献[26],26页。中国古代算学直角三角形直角边命名方式有两种,或横者为句,纵者为股,或短者为句,长者为股,李氏所用为前者。至于象限仪上的影矩样式,则包含在《测量全义》第3卷“造矩度法”中,其“约法”(图31)谓“象限弧之内空作矩度,其窥衡指线上分即矩度边之分,是指线当权线也,为用殊大”([71],9b页),即在象限仪弧边之内另作影矩与仪同心,并借其窥衡为用,作为矩度的简约形式。

图30 《浑盖通宪图说》所示平仪仪背下部方仪([62],下卷,24b页)
3 圆边几何矩:“小象限”及其西方渊源
前揭《测量全义》第3卷所附的仪器制作与使用解说,白尚恕认为“可能是参考有关论著自行编写的”([72],148页),但未给出具体来源。“造象限仪法”“造矩度法”所示明确,已见前述,而“造小象限法”具体何指,则有待考证。
3.1 “小象限”:形制、用法与属性

图32 《测量全义》所示 “小象限”([71],10b页)
就名称而言,“小象限”应与象限仪有关。《测量全义》“造象限仪法”题注曰:“篇中或省曰象限,或曰仪”([71],6a页)。依此,“小象限”当是“小象限仪”的省称,似是一种体型较小的象限仪。然而,书中对该仪器(图32)的具体描述却非如此:
正方版一角为心,作象限之弧,弧外两边二平分之,又三平分之,至四、至五、六、七、八、九、十各平分,用界尺从心至各分为界,弧上作疏密线,线以内书各分。其弧外余板去之。加权线,与矩度同用。
用法 以表向物如前,遇权线截弧表之旁,则高多远少;截表之对边,则高少远多。如截表旁为二分,则远一高二;截五分,则远一高五。反之,则高一远二、高一远五。说见二卷矩度法中。
又法:以甲乙边当一百,依前法,分乙戊弧为一百不平分。若权线至己,则股一百句五十也;至辛,则股一百句一十也。转用之,权线至庚,则甲丁股一百句五十也。([71],10b~11a页)*引文第2段内“高一远五”,原作“远一高五”,显误,今据意校正。
该仪器在正方板上作象限弧,且“弧外余板去之”,实与象限仪外形一致,但又“与矩度同用”。以上考察表明,象限仪与矩度一量角度、一量分度,功能差异十分显著。“小象限”象限弧上所作“疏密线”即“不平分”的标度,乃是相对于象限仪象限弧上的均分弧度标度而言,故非量取角度之用,而所谓“远一高二”“股一百句一十”等,显然是据所测分度推得的实际高远比例,由此判断,该器当属于矩度即几何矩。
3.2 从矩边向弧边投射:“小象限”的制作方式
“小象限”既是几何矩之一种,其弧边非均分标度如何表示原矩边之上的分度?同一象限弧之上又如何区分“弧表之旁”与“表之对边”?考察其具体作法“用界尺从心至各分为界,弧上作疏密线”,并结合图示寻绎,可知所谓“疏密线”是弧心与弧外原有两直边诸均匀分点的连线在象限弧之上的相应痕迹,也就是说,“小象限”的标度实际是弧外直边分点在弧边的投射(projection),弧外直边均匀分布的分度标度由此对应转换为弧边疏密不一的分度标度。因此,虽然该器器身仅保留象限弧,却可由权线所指弧边标度“与矩度同用”,而所谓“弧表之旁”与“表之对边”即对应于窥表旁边的直影和窥表对边的倒影的两条半象限弧。
“小象限”的构造方式自有其西方背景。象限仪与几何矩皆具一直角,窥望、读数等使用方式一致,自然生发出合二者为一体的设计取向,前揭几何象限仪即其典型。但几何象限仪只是将两种仪器的外形予以简单组合,而“小象限”则是以象限仪的形态实现几何矩的功能,其中的设计思想与技术关键就在于均分点投射的方法。事实上,中世纪阿拉伯学者在星盘之上引入影矩后不久,就已使用该法加以改进:或无限延长直边并按原有分度续作划分和标示,再以其各分点向弧边投射(图33),如此可以直接读取足够大的直影分度而毋须通过倒影分度换算;或在象限弧内、影矩外作斜线,再以直影、倒影各分点投射其上(图34),如此可以放大两影边起始部分以便作出清晰的细分标度而获得更为准确的读数([30],69~70,72~73页)。比照上述两种方式,即可看出“小象限”从矩边直、倒二影向弧边投射的技术与设计传统所在。
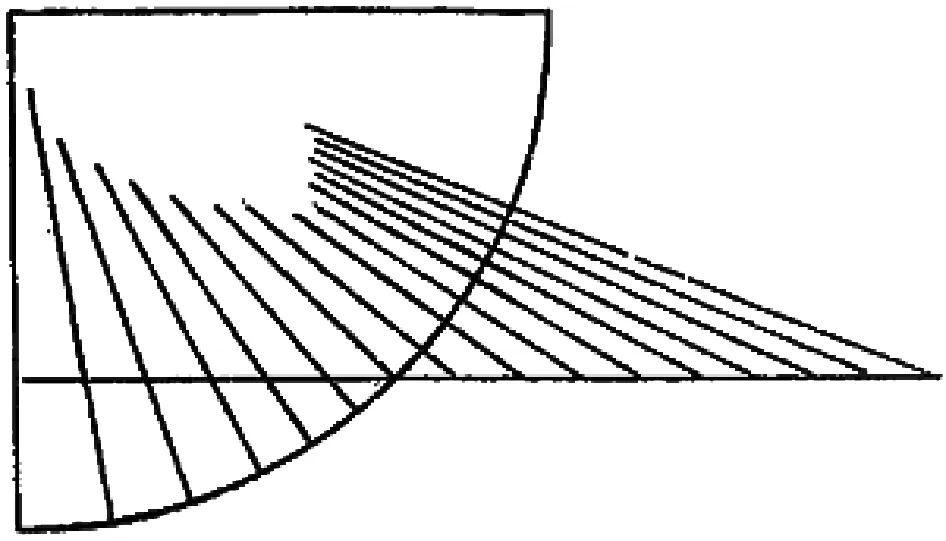
图33 影矩分度投射一([30],69页,Figure 27)

图34 影矩分度投射二([30],73页,Figure 29)
3.3 阿皮安及其发明的象限仪:“小象限”的欧洲来源
“小象限”的形制可以追溯到德意志天文学家、制图学家阿皮安(Peter Apian,1495 ~ 1552)的设计发明与相关著作。阿氏活跃于文艺复兴盛期,长期在因戈尔施塔特(Ingolstadt)任数学教授,论著颇丰,其《宇宙学之书》(CosmographicusLiber,1524)[83]为一时经典,经修订、转译后更在欧洲广泛流传。[84]正是在该书中,阿氏将近代制图学奠基于数学理论与测量实践之上([30],110页)。*1533年,荷兰探险家、制图学家、数学家弗里修斯(Gemma Frisius, 1508~1555)在安特卫普第2次为阿皮安出版《宇宙学之书》时,将自著Libellus de locorum describendorum ratione附后,其中首次提出通用的三角测量方法,成为此后欧洲大地测量的理论先声,参见文献[30],110页;[85]。他在天文、测量仪器上也有诸多创新与改进工作,“小象限”即与其中一种象限仪有关。《阿皮安天文象限仪:最近发明而现在首次发行》(QuadransApianiAstronomicusetIamRecensInventusetNuncPrimumEditus, 1532)6章[86]是介绍该器的专书,其增补本《仪器之书》(InstrumentBuch,1533)8卷[87]则以德文刊行。书中所示象限仪正面(图35)画有功能不一的诸多组件,最外层为均匀标示0 ~ 90递增弧度数值的象限弧(FG),而相邻的另一象限弧(HI)自两端至中心双向标示0 ~ 100递增数值,与窥表相近、相远的两端还分别书有“VMBRA·RECTA”“VMBRA·VERSA”字样([86],fol.A3r;[87],fol.A3r),对应解说又称其用作高远测量([86],fol.A3v,Propositio Tertia),由此可知此弧即影矩,依其外形可称作圆边影矩(circular shadow square)([30],166页)。这种变体形式的影矩也正是此象限仪设计的重要创新之处,阿皮安在书中专辟一卷具体介绍其各类测量方法(图36)([86],fol.D1v~E3r;[87],
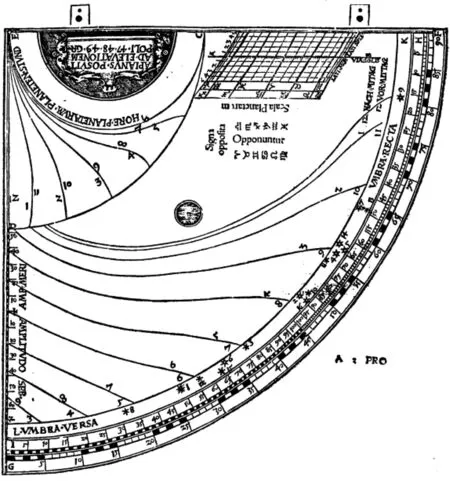
图35 阿皮安的象限仪([86],fol.A3r)
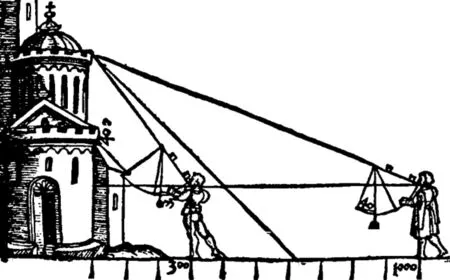
图36 用阿皮安象限仪之圆边影矩测高(前直影75分度,后倒影40分度)([86],fol.D2r)
fol.E3r~G2v)。今以“小象限”与之比观,两者形态、功能一致,故阿皮安发明的设有圆边影矩的象限仪,应即《测量全义》中“小象限”的最初原型。唯后者虽仍以“象限”名之,但器身之上并无一般象限仪的弧度标度,而只设圆边影矩,因而成为形如象限仪而用如几何矩的独立仪器,比于圆边影矩,可称作圆边几何矩。
值得指出的是,阿皮安惯于在仪器设计中使用投射方式。如《宇宙学之书》中用于天体观测的十字杆的角度标度,系象限弧弧度均分点沿半径线向主干直边投射而成([83],fol.30~32)(图37),这种从圆边向直边的投射正与“小象限”相反,前述《测量全义》古弧矢仪主干“以度分分之”“一法”([70],卷10,14b~15a页)(图38)即与之类似。*但所用两者所用投射方式不尽相同,尚有一定差别。

图37 阿皮安《宇宙学之书》所示天体观测用十字杆主干角度标度投射方式([83],fol.32)

图38 《测量法义》所示古弧矢仪主干“度分”分法([70],卷10,13b页)
阿皮安设计的影矩形制曾有相当的影响,如意大利科学巨匠伽利略(Galileo Galilei,1564 ~ 1642)所作比例规(geometric and military compass),其两规脚之间的象限弧(图39)上亦采用这种圆边影矩。*伽利略对其比例规象限弧上圆边影矩的描述与用法介绍见《几何与军事用规的操作方法》(Le operazioni del compasso geometrico et militare)“Diversi Modi per Misvrar con La Vista”部分([88],fol.23v~34r)。比例规器形图示未载该书意大利文初版(1606),而首见于拉丁文初版(1612),图39截取自意大利文再版(1649)([89],附图页)。又,Stillman Drake曾认为此设计是将塔塔利亚的几何矩改方为圆的结果,参见文献[52],107~108页。伽利略的比例规著作与阿皮安的《仪器之书》均曾入藏北堂(编号1655,3886)[90],《测量全义》的“译撰”者罗雅谷与“同订”者汤若望([71],题名页)分别系意大利和德意志人,应当熟悉前两者的著作,圆边影矩应是经由其手采译、撰述,成为《测量全义》所引介的高远测量知识的一部分。*伽俐略所作比例规使用时象限弧弧背向下,而此象限弧图示弧背向上,故标度数字皆倒置。
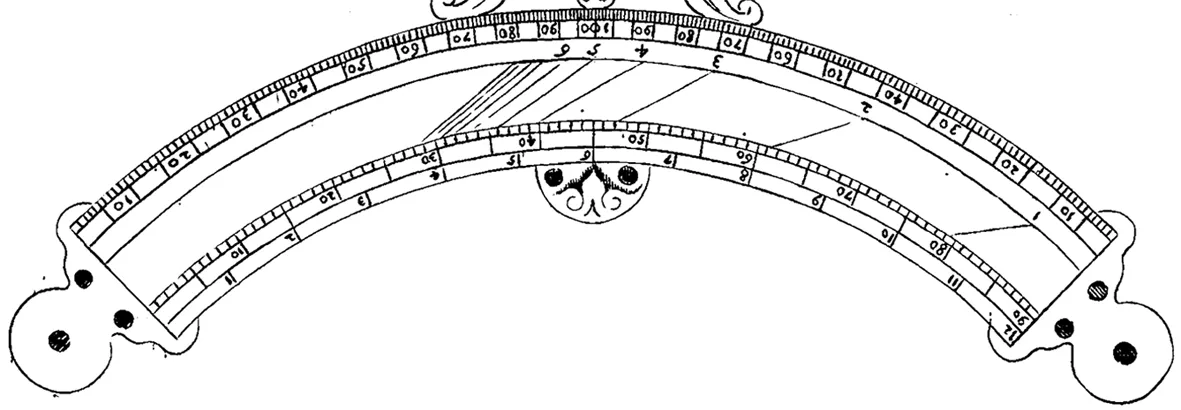
图39 伽利略比例规的象限弧([89],附图页)①
3.4 百分度与整比值:“小象限”的两种标度方式
前引“小象限”的描述中,存在两种不同的弧边标度。其一如“又法”所言,“以甲乙边当一百,依前法,分乙戊弧为一百不平分”,即将原弧外两直边均分为100分,再将分点投射于弧边,所得圆边影矩的直影、倒影标度呈两边对称、中间密而两端疏的非均匀分布,数值自两端0递增至中心100。这一标度方式与前述阿皮安象限仪和伽利略比例规的圆边影矩设计完全一致,乃是依原矩边直、倒二影100分分度转换而得。
至于另一种标度方式,则须首先将“弧外两边二平分之,又三平分之,至四、至五、六、七、八、九、十各平分”,但象限弧上的标度具体如何,《测量全义》言之未详,相应“用法”则称:“如截表旁为二分,则远一高二;截五分,则远一高五。”据此推断,弧边标度“二分”“五分”应与原直影边二分之一点和五分之一点相对应,而此种标度的完整制作过程应当是:对弧外原有两直边作2等分、3等分至10等分,将其中首个等分点即1/2、1/3…1/10各点次第取出,再将它们及两直边交点(起始点)投射于象限弧上。所得标度同样呈对称分布,但中间疏而两端密,数值自中心1向两端递增至10(10处并非端点)。这种标度便于直接读取高程与远距之比(倒影反之),但由于整比标度之间的部分无法或不便读取,精确性则远逊于前者。我们亦可在当时的欧洲仪器上看到这种设计的实际应用,如一具1676年英国制象限仪正面,就有自中心向两端由疏渐密分布标度的象限弧(图40,双箭头弧线所示),并标写数字1、2、3、4、5、10等,1~5各标度之间尚有1/4、1/2与3/4细分标度;*英国国家海事博物馆(The National Maritime Museum)藏,藏品号NAV1036。参见文献[91]。而一具1614年德国制星盘,其仪背影矩直影除原有的12分以外,上方也刻有数值1 ~ 6的整比标度(图41)。*俄国冬宫隐士庐博物馆(The State Hermitage Museum)藏,收藏号ЭРТх-1262。该星盘为彼得大帝(Tsar Peter I, 1672~1725)幼年习用之物,参见文献[92]。两种标度方式的特点可总结如下(表1)。


表1“小象限”象限弧的两种标度方式

标度方式标度数值内涵标度数值范围标度数值递增方向等隔标度分布特征附注百分度原直、倒影分度值双向0~100从两端向中间递增两端舒中间密0为两端标度整比值表与直、倒影比值双向1~10从中间向两端递增中间疏两端密10非两端标度

4.1 《度测》:陈荩谟的高远测量专论
《度测》三卷,约成于崇祯十三年(1640),今有抄本传世([95],40~41页)。*除李俨原藏抄本即文献[96]外,另一抄本藏台湾“国家图书馆”,参见文献[97],17页。在自叙中,陈荩谟首述古代算学源流,并特别强调《周髀算经》的经典地位;次谓明代算学日渐衰微,儒士罔闻而难知,继而称:
泰西来宾,斯学始备,大方家多传之,徐玄扈先生有《测量法义》《句股义》。是《周髀》者,句股之经;《法义》者,句股之疏传也。……谟爰撰兹编,首诠算经,次胪诸法,合古今而浅言之,出以己意,发凡绘图,庶几《周髀》大彰,《法义》弥著,以便有志经济之习之者。([96],291~292页)
推崇《周髀算经》的同时,陈氏亦充分肯定《测量法义》的价值,将这一西学著作为前者的重要解说,希冀以西方数学羽翼传统算术,而裨益实学,经济时世。*应予特别指出的是,这种认知态度和学术策略与此后的“西学中源”尚有相当的差别。是故全书三卷,上卷疏解《周髀》首章,“使学者溯矩度之本,其来有自,以证泰西立法之可据”([96],330页),并阐述矩度形制及相关原理和算法;中、下两卷则在《周髀》“用矩之道”即“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”([98],10a页)的框架下,加入“弦矩以见广”([96],387~409页),讨论各类矩度测量方法([26],28~32页)。
陈荩谟对中西学术平衡、会通的态度,时人多有推重,如清初历算大家梅文鼎(1633 ~ 1721)作为其晚辈曾有诗赞曰:“耆儒推槜李,能兼两法并,《象林》存古占,西测详纵衡”,并注称“槜李陈献可先生年过八十,著述甚富,余惟见《象林》《度算》二书及所制矩度器,皆精核无伦。”[99]可见陈氏德望素隆,其所著书与所制器并行于世,颇具声誉。
4.2 “菴矩度”:结合矩度和“小象限”的独特设计
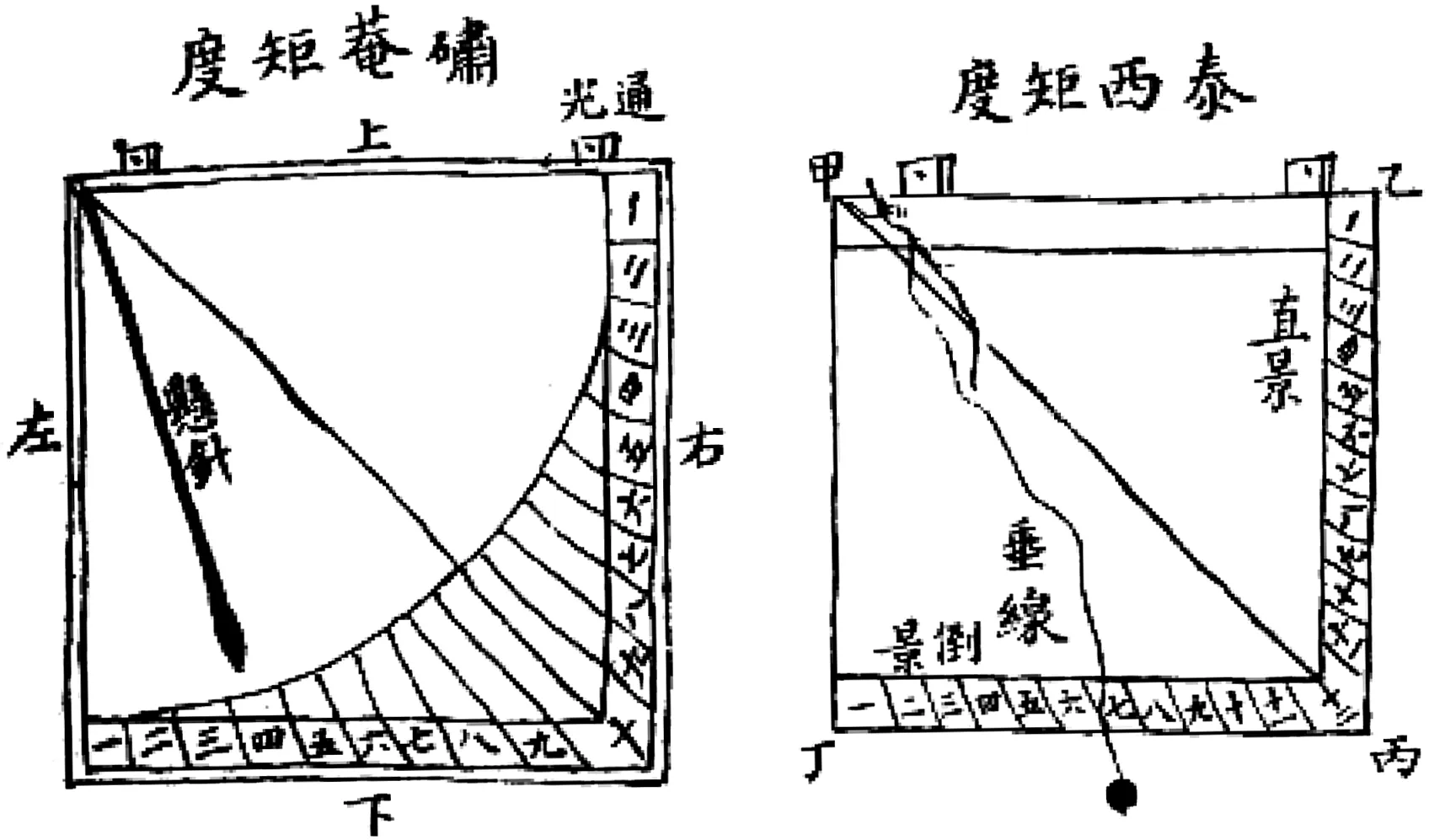
图42 陈荩谟对《测量法义》所载矩度形制的改造([96],333页)

事实上,《崇祯历书》的主体部分至崇祯七年末(1635初)已陆续刊出([95],33~34,36~37页),而这些书籍或其知识内容完全可能借由教会、家族、师友等人脉网络,以传阅、抄录等方式为留心西学的士人及时接触和掌握。如崇祯十一年(1638)二月前,薄珏(活跃于崇祯间)、魏学濂(1608~1644后)等就已在毗接秀水的同府嘉善县阅读、研习《崇祯历书》中的核心天文历法理论,并撮抄、汇集、演撰成相关著作。[101]陈荩谟也很有可能在崇祯十三年之前通过其师友如黄道周、方以智(1611~1671)等人获读包括《测量全义》在内的《崇祯历书》或其部分内容,从而将“小象限”的形制与功能融入到他对“泰西矩度”增改之中。
4.3 双向诠释:陈荩谟对“小象限”的接纳方式

矩之内体,毁方而为圆,信圆之周则成句;矩之外体,破圆而为方,展方之匝则成股,肖大圆、大方四象之一也。赵君卿曰:“体方则度景正,形圆则审实难。盖方者有常,而圆者多变,故当制法而理之。”今此矩度,盖尽方圆之法矣。([96],334页)
此中言及的方圆之辨,乃是中国古代算学传统的经典话题,而《周髀算经》首章商高答周公问则是其重要渊源之一。如前所论,《度测》全篇实以彰明《周髀》古义为宗旨,此番诠释就是一例。其首句化用自赵君卿注“数之法出于圆方”之说,所谓:
圆径一而周三,方径一而匝四。伸圆之周而为句,展方之匝而为股,共结一角,邪适弦五,此圆、方、邪径相通之率,故曰数之法出于圆方。([98],1a页)
如此一来,矩度内外的圆方之形与作为测望基础的勾股之论就得以相互联系。次句则明引赵注,意欲说明将影矩标度引线至象限弧的作用——按陈氏之意,方圆各边分点之间的投射与相连似与“方者有常,而圆者多变,故当制法而理之”若合符契。但所谓“制法而理之”,是以方理圆,本应有圆曲在先,而后以方应之,陈氏在矩边内增添圆弧的作法恰与此相反。更重要的是,这段赵注本是为《周髀》原文“方数为典,以方出圆”而作,其下接续言道:
理之法者,半周、半径相乘,则得方矣。又可周、径相乘,四而一。又可径自乘,三之,四而一。又可周自乘,十二而一。故圆出于方。([98],10b页)*注意此中“半周、半径相乘,则得方矣”之“方”当解作圆形之积,而非方形。考《九章算术》“圆田术”,“半周、半径相乘,得积步”下刘徽注曰“按:半周为从,半径为广,故广、从相乘为积步也”([102],20页),即圆半周、半径各当方形长、宽以入于方田术之意,因称其积为“方”。承林力娜(Karine Chemla)教授就此为笔者指明解惑,特此致谢。
所言均是圆形面积算法。是故赵注的“制法而理之”,意在为“形圆”者“审实”,即推求圆积,陈氏所释意涵显然与之相远。

5 余 论
总结以上考察可知,西方高远测量仪器的主要类型均已在明季引介入华(表2),既有几何矩、象限仪等专门仪器,也有平面镜、矩尺等简单用具;既有表这样的古老用具,也有圆边影矩这样的新近发明。其中一项显著差异是,配合平面三角形解法推算的角度量取仪器只有象限仪,而基于长度比例关系推算的仪器则种类丰富,兼有样式变化,直接读取比例长度的分度测量仪器则是其主体,并在最先引介之列。后者虽器形新异而引人注目,其原理却契合中国古代测望学说依赖比例计算的知识传统,易为受众接受和研习。事实上,随着三角学知识的传播,西方17世纪开始的大地测量活动越来越趋向于使用象限仪作角度测量,几何矩及作为仪器功能组件的影矩则日益失其流行之势([30],154页)。然而同一时期明季高远测量仪器的引介却仍以后者为重点,至于象限仪则要等到清康熙年间用以实施全国大地测绘[103- 104]并将相关知识系统编纂入《数理精蕴》之后,才逐渐获得实质性的接受。这一现象充分表露出来华耶稣会士在引介西方知识时有意适应乃至迎合中国本土传统的精心考量与积极努力。

表2 明季引介的西方高远测量仪器(或仪器功能组件)
《测量全义》第3卷介绍“小象限”,虽形如象限仪,却用如几何矩,以所测分度推算实际高远距离。它通过投射方式将几何矩的矩边标度转换至象限仪的弧边之上,成为几何矩的一种变体,而很可能源自阿皮安设计发明的象限仪上设置的圆边影矩或类似设计。当时欧洲正处于新知新见不断涌现的科学革命时期,来华的耶稣会士们在以经典理论为总体框架输入西学的同时,也往往努力将欧洲最新发展的知识零星地予以介绍,“小象限”就是这类介绍的一个典型案例。
明季传入的西洋仪器亦引起中国士人的关注与兴趣,掌玩其器、研习其说成为知识界的一时风尚。崇祯末年,嘉兴儒士陈荩谟设计的内含象限弧且弧线标度与矩边标度对应相连的矩度样式,很可能直接受到《测量全义》“小象限”的启发。另一方面,他积极推阐中国传统算学经典《周髀算经》的注释文句,赋予自己的矩度样式以合乎经典古义的解释。我们可以由此审视明季输入的西学知识对晚明学者的实质影响,以及他们在旧有学术传统中接纳这些新知的态度、策略与具体方式。
致谢本文系据笔者博士学位论文部分章节增订而成。论文撰写和修改过程中,业师韩琦先生给予悉心指导和具体意见,Jens Høyrup教授、林力娜(Karine Chemla)研究员各就相关疑难问题作出解答,周维强副研究员、孙承晟副研究员提出诸多中肯建议,谨此并致谢忱。
1 利玛窦. 耶稣会与天主教进入中国史[M]. 文铮, 译. 梅欧金(Engenio Menegon), 校. 北京: 商务印书馆, 2014.
3 黄一农. 红衣大炮与明清战争——以火炮测准技术之演变为例[J]. 清华学报, 1996, 新26(1): 31~70.
4 戴念祖. 明清之际望远镜在中国的传播与制造[J]. 燕京学报, 2000, 新(9): 123~150.
5 张柏春. 明清测天仪器之欧化: 十七、十八世纪传入中国的欧洲天文仪器技术及其历史地位[M]. 沈阳: 辽宁教育出版社, 2000. 94~160.
6 许洁. 明清时期西式天文测时仪器的传入及其影响[D]. 合肥: 中国科学技术大学. 2006.
7 王广超. 明清之际圭表测影考[J]. 中国科技史杂志, 2010, 31(4): 447~457.
8 李俨. 中国数学史导言[J]. 学艺, 1933, 百号纪念增刊: 139~160.
9 韩琦. 康熙时代传入的西方数学及其对中国数学的影响[D]. 北京: 中国科学院自然科学史研究所. 1991.
10 韩琦, 詹嘉玲. 康熙时代西方数学在宫廷的传播——以安多和《算法纂要总纲》的编纂为例[J]. 自然科学史研究, 2003, 22(2): 145~156.
11 冯立昇. 中国古代测量学史[M]. 呼和浩特: 内蒙古大学出版社, 1995.
12 潘澍原. 会通中西: 明清之际句股与测望知识的转变[D]. 北京: 中国科学院自然科学史研究所. 2016.
13 李俨. 重差术源流及其新注[J]. 学艺, 1926, 7(8): 1~15.
14 Baron R. Hugonis de Sancto VictorePracticaGeometriae[J].Osiris, 1956, 12: 176~224.
15 Baron R. Note sur les Variations au XIIesiècle de la Triade Géométrique Altimetria, Planimetria, Cosmimetria[J].Isis, 1957, 48(1): 30~32.
16 Homann F A. Introduction[M]Hugh of Saint-Victor.PracticalGeometry. Homann F A (trans). Milwaukee: Marquette University Press, 1991. 1~30.
17 L’Huillier H. Practical Geometry in the Middle Ages and Renaissance[G]Grattan-Guinness I (ed).CompanionEncyclopediaoftheHistoryandPhilosophyoftheMathematicalSciences. Vol.1, London: Routledge, 1993. 185~191.
18 Vogel K. Ein Vermessungsproblem reist von China nach Paris[J].HistoriaMathematica, 1983, 10(3): 360~367.
19 沈康身. 我国古代测量技术的伟大成就[J]. 科学史集刊, 1965, 8期: 28~41.
20 吴文俊. 我国古代测望之学重差理论评介——兼评数学史研究中某些方法问题[J]. 科技史文集, 1982, 8辑: 10~30.
21 白欣. 西学传入之初的中日测量术[D]. 西安: 西北大学, 2006.
22 冯锦荣. 方中通及其《数度衍》——兼论明清之际纳白尔、哥白尼、开普勒、伽利略等之历算作品在华流播的情形[J]. 论衡, 1995, 2(1): 123~204.
23 馮錦栄. 中国知識人の西洋測量学研究——明末から清末における[C]狭間直樹. 西洋近代文明と中華世界: 京都: 京都大学人文科学研究所70周年記念シンポジウム論集. 京都: 京都大学学術出版会, 2001. 354~373.
24 冯锦荣. 乾嘉时期考据学与历算研究的一些问题[C]林庆彰, 张寿安. 乾嘉学者义理学. 台北: “中央”研究院中国文哲研究所, 2003. 733~766.
25 冯锦荣. 清初西洋测量学的发展——以陈訏(1650~1732)及其《勾股述》为例[C]单周尧, 李焯然, 王润华. 东西方文化承传与创新: 赵令杨教授荣休纪念论文集. 新加坡: Uni Press, National University of Singapore, 2004. 136~160.
26 姚妙峰. 西方矩度测量知识的传入与影响[D]. 上海: 上海交通大学. 2015.
27 Turner G L’E.AntiqueScientificInstruments[M]. Poole: Blandford Press, 1980. 16~18.
28 Bennett J A.TheDividedCircle:AHistoryofInstrumentsforAstronomy,NavigationandSurveying[M]. Oxford: Phaidon-Christie’s, 1987.
29 Leonardo of Pisa (Fibonacci).LaPracticaGeometriaediLeonardoPisano[M]. Boncompagni B (ed).ScrittidiLeonardoPisano,matematicodelsecolodecimoterzo. Vol.2. Rome: Tipografia delle scienze matematiche e fisiche, 1862. 1~224.
30 Kiely E R.SurveyingInstruments:TheirHistoryandClassroomUse[M]. New York: Bureau of Publications, Teachers College, Columbia University, 1947.
31 Magini G A.DePlanisTriangulisLiberVnicus.EiusdemDeDimetiendiRationeperQuadrantem, &GeometricumQuadratum,LibriQuinque[M]. Venice: Robertus Meiettus. 1592.
32 Lewis M J T.SurveyingInstrumentsofGreeceandRome[M]. Cambridge: Cambridge University Press, 2001.
33 Finè O.Dere&praxigeometrica,Libritres,figuris&demonstrationibusillustrate[M]. Paris: Aegidium Gourbinum, 1556.
34 Münster S.RudimentaMathematica[M]. Basel: Heinrich Petri, 1551
35 Rosen E. Regiomontanus, Johannes[G]Gillispie C C (ed).DictionaryofScientificBiography. Vol.11. New York: Charles Scribner’s Son, 1975. 348- 352.
36 Zinner E.Regiomontanus:HisLifeandWork[M]. Brown E (trans). New York: North-Holland, 1990.
37 钱宝琮. 中国数学史[M]. 北京: 科学出版社, 1964. 244.
38 严敦杰. 明清之际西方传入我国之历算记录[C]梅荣照主编. 明清数学史论文集. 南京: 江苏教育出版社, 1990. 114~181.
39 罗雅谷, 龙华民, 汤若望, 等. 月离历指[M]. 崇祯五年(1632)刻本.
40 陈梦雷, 蒋廷锡. 古今图书集成[G]. 民国二十三年(1934)中华书局影印雍正内府铜活字本.
41 Bruyns W F J M.TheCross-Staff:HistoryandDevelopmentofaNavigationalInstrument[M]. Zutphen: Walburg Pers, 1994.
42 Engelfriet P M.EuclidinChina:TheGenesisoftheFirstChineseTranslationofEuclid’sElements,BooksI-VI(Jiheyuanben,Beijing, 1607)andItsReceptionupto1723[M]. Leiden: Brill, 1998.
43Geometriaincertiauctoris[M]. Bubnov N (ed).GerbertiposteaSilvestriIIpapaeOperaMathematica(972-1003). Berlin: Friedländer, 1899. 310~365.
44 Peurbach G.QuadratumGeometricumpraeclarissimiMathematiciGeorgiiBurbachii. Nuremberg: Johannes Stuchs, 1516.
45 Hellman C D, Swerdlow N M. Peurbach, Georg[G]Gillispie C C (ed).DictionaryofScientificBiography. Vol.15. New York: Charles Scribner’s Son, 1978. 473~479.
46 Bernard H.MatteoRicci’sScientificContributiontoChina[M]. Werner E C (trans). Peiping: Henri Vetch, 1935.
47 冯锦荣. 明万历版利玛窦辑、毕懋康演、佘永宁刊刻《乾坤体义》蠡探——兼论利玛窦对《节本托勒密天文学大成》的校算工作及耶稣会的知识观[C]北京外国语大学中国海外汉学研究中心, 中国近现代新闻出版博物馆. 西学东渐与东亚近代知识的形成和交流. 上海: 上海人民出版社, 2012. 342~374.
48 Hashimoto K (橋本敬造).HsüKuang-ch’iandAstronomicalReform:TheProcessoftheChineseAcceptanceofWesternAstronomy1629~1635[M]. Osaka: Kansai University Press, 1988.
49 江晓原. 明末来华耶稣会士所介绍之托勒密天文学[J]. 自然科学史研究, 1989, 8(4): 306~314.
50 Tartaglia N.NovascientiainventadaNicoloTartalea[M]. Venice: Stephano da Sabio, 1537. fol.H4v~L3r.
51 Valleriani M (ed).Metallurgy,BallisticsandEpistemicInstruments:TheNovaScientiaofNicolòTartaglia.ANewEdition[M]. Edition Open Access, 2013.
52 Drake S. Galileo and the First Mechanical Computing Device[J].ScientificAmerican, 1976, 234(4): 104~113.
53 Hulsius L.DeQuadranteGeometricoLibellus[M]. Nuremberg: Christoph Lochner, 1594.
54 冯锦荣. 明末清初士大夫对《崇祯历书》之研究[J]. 明清史集刊, 1997, 3: 145~198.
55 Clavius C.GeometriaePracticae[M]. Rome: Aloisius Zannetti, 1604.
56 Charette F, Schmidl P G. al-Khwārizmī and Practical Astronomy in Ninth-Century Baghdad. The Earliest Extant Corpus of Texts in Arabic on the Astrolabe and Other Portable Instruments[J].SCIAMUS, 2004, 5: 101~198.
57 Proctor D. The Construction and Use of the Astrolabe[G]Van Cleempoel K (ed).AstrolabesatGreenwich:ACatalogueoftheAstrolabesintheNationalMaritimeMuseum. Oxford: Oxford University Press, 2006. 15~22.
58 安大玉. 明末平仪(Planispheric Astrolabe)在中国的传播——以《浑盖通宪图说》中的平仪为例[J]. 自然科学史研究, 2002, 21(4): 299~319.
59 安大玉. 明末西洋科学東伝史: 『天学初函』器編の研究[M]. 東京: 知泉書館, 2007.
60 Stöffler J.Elucidatiofabricaeususqueastrolabii,aIoanneStoflerinoIustingensiviroGermano;atquetotiusSphericedoctissimonuperIngenioseconcinnataataqueinIucemedita[M]. Oppenheim: Jacob Köbel, 1513. fol.74r.
61 刘明强. 万历韶州同知刘承范及其《利玛传》[J]. 韶关学院学报·社会科学, 2010, 31(11): 1~8.
62 李之藻, 郑怀魁. 浑盖通宪图说[M]. 万历三十五年(1607)丽水樊良枢刻本.
63 利玛窦, 徐光启. 测量法义[M]. 天学初函本.
64 徐光启. 测量异同[M]. 天学初函本.
65 利玛窦, 李之藻. 同文算指通编[M]. 卷6. 明万历四十二年(1614)刻本.
66 武田楠雄. 同文算指の成立[J]. 科学史研究, 1954, 30號: 7~14.
67 D’Elia P M (ed).FontiRicciane:documentioriginaliconcernentiMatteoRiccielastoriadelleprimerelazionitral’EuropaelaCina(1579~1615)[M]. Vol.2. Rome: La Libreria dello Stato, 1949. 358.
68 杨泽忠. 李之藻与西方几何在我国的传播[J]. 数学教学, 2009,(7): 42~45.
69 徐光启. 徐光启集[M]. 王重民, 辑校. 北京: 中华书局, 1963.
70 罗雅谷, 龙华民, 汤若望, 等. 测量全义[M]. 崇祯四年(1631)刻顺治二年(1665)重修西洋新法历书本.
71 罗雅谷, 龙华民, 汤若望, 等. 测量全义[M]. 卷3. 法国国家图书馆(Bibliothèque nationale de France)藏崇祯四年(1631)刻本(Chinois 4873).
72 白尚恕. 《测量全义》底本问题的初探[J]. 科学史集刊, 1984, 11期∶143~159.
73 熊三拔, 徐光启. 简平仪说[M]. 天学初函本. 2b.
74 关增建. 传统365 1/4分度不是角度[J]. 自然辩证法通讯, 1989, 11(5): 77~79.
75 黄一农. 极星与古度考[J]. 清华学报, 1992, 22(2): 93~117.
76 Ryff W H.DerfurnembstennotwendigstendergantzenArchitecturangehörigenmathematischenKünst[M]. Das drit Buch. Nuremberg: Johan Petreius, 1547.
77 徐光启. 玄扈先生量算河工及测验地势法[M]徐光启. 农政全书. 卷14. 崇祯十二年(1639)平露堂刻本. 18a~23b.
78 王重民. 徐光启[M]. 何兆武, 校订. 上海: 上海人民出版社, 1981. 21~24.
79 梁家勉. 徐光启年谱[M]. 上海: 上海古籍出版社, 1981. 81.
80 熊三拔, 周子愚, 卓尔康. 表度说[M]. 天学初函本.
81 Belli S.LibrodelMisurarconlaVista,diSilvioBelliVicentino[M]. Venice: Giordano Ziletti, 1566. 2~6.
82 Clavius C.Astrolabium[M]. Rome: Bartholomaeus Grassus, 1593. 555~566.
83 Apian P.CosmographicusLiberPetriApianiMathematiciStudioseCollectus[M]. Landshut: Joannes Weyssenburger. 1524.
84 Kish G. Apian, Peter[G]Gillispie C C (ed).DictionaryofScientificBiography. Vol.1. New York: Charles Scribner’s Son 1970. 178~179.
85 Pogo A. Gemma Frisius, His Method of Determining Differences of Longitude by Transporting Timepieces (1530), and His Treatise on Triangulation (1533)[J].Isis, 1953, 22(2): 469~506.
86 Apian P.QuadransApianiAstronomicusetIamRecensInventusetNuncPrimumEditus[M]. Ingolstadt: Peter Apian, 1532.
87 Apian P.InstrumentBuch,durchPetrumApianumerstvonnewbeschriben[M]. Ingolstadt: [s.n], 1533.
88 Galilei G.Leoperazionidelcompassogeometricoetmilitare[M]. Padua: Pietro Marinelli, 1606.
89 Galilei G.Leoperazionidelcompassogeometricoetmilitare[M]. Padua: Paolo Frambotto, 1649.
90 Verhaeren H G.CatalogueofthePei-T’angLibrary[M]. Peking: Lazarist Mission Press, 1949. 482, 1123.
91 Higton H (ed).SundialsatGreenwich:ACatalogueoftheSundials,Nocturnals,andHoraryQuadrantsintheNationalMaritimeMuseum[G]. Oxford: Oxford University Press, 2002. 343~344.
92 Maslikov S. Peter the Great’s Astrolabe Celebrates 400th Anniversary[J].BulletinoftheScientificInstrumentSociety, 2015, no.124: 10~15.
93 冯锦荣. 陈荩谟(1600?~1692?)之生平及西学研究——兼论其著作与马礼逊(Robert Morrison, 1782~1834)《华英字典》之中西学缘[J]. 明清史集刊, 2007, 9: 209~262.
94 盛枫. 嘉禾征献录[G]. 盛支焯, 校订. 46卷. 民国二十五年(1936)嘉兴金氏刻槜李丛书本.
95 李俨. 明清之际西算输入中国年表[M]中算史论丛第三集. 北京: 科学出版社, 1955.
96 陈荩谟. 度测[M]. 续修四库全书1044册影印中国科学院自然科学史研究所藏李俨原藏抄本. 上海: 上海古籍出版社, 2002. 291~466.
97 刘钝. 访台所见数学珍籍[J]. 中国科技史料, 1995, 16(4): 8~21.
98 周髀算经[M]. 赵君卿, 注. 甄鸾, 重述. 李淳风等, 注释. 卷上. 影印南宋嘉定六年(1213)鲍澣之刻本. 北京: 文物出版社, 1980.
99 梅文鼎. 送章颖叔归山阴(其三)[M]梅文鼎. 绩学堂诗钞[M]. 卷2. 乾隆刻本. 2b.
100 陈荩谟. 度算解[M]. 续修四库全书1044册影印中国科学院自然科学史研究所藏李俨原藏抄本. 上海: 上海古籍出版社, 2002. 527~556.
101 郑诚. 薄珏天文学著作新证[J]. 中国科技史杂志, 2015, 36(2): 142~157.
102 九章算术[M]. 刘徽, 注. 李淳风等, 注释. 郭书春, 汇校. 卷1. 郭书春. 九章算术新校. 合肥: 中国科学技术大学出版社, 2014.
103 翁文灏. 清初测绘地图考[J]. 地学杂志. 1930, 18(3): 1~34.
104 Han Qi (韩琦). Cartography during the Times of the Kangxi Emperor: The Age and the Background[M]Ribeiro R M, O’Malley J W (eds).JesuitMapmakinginChina:D’Anville’s‘NouvelleAtlasdelaChine’(1737). Philadelphia: Saint Joseph’s University Press, 2014. 51~62.

