《宝莉莎历数书》中的行星运动理论

唐 泉 万映秋

(1.咸阳师范学院数学与信息科学学院,陕西 咸阳 712000；2.李约瑟研究所,英国剑桥,CB3 9AF； 3.咸阳师范学院文学与传播学院,陕西 咸阳 712000)

《五大历数全书汇编》(Pacasiddhāntikā)是古代印度一部重要的数理天文学著作。该书作者伐罗诃密西罗(Varhamihira)生年不详,约卒于公元587年,是印度早期最重要的天文学家和星占学家之一,其研究兴趣涉及数理天文学、星占学和年代学等多个方面。《五大历数全书汇编》所取近距历元为公元505年,按照当时印度天文学著作的习惯,其成书年代略晚于其所取近距历元,由此推测《五大历数书汇编》大约成书于公元6世纪中叶。

作为古代印度一部重要的数理天文学著作,《五大历数全书汇编》一直受到科学史家的高度关注,先后出现了三个影响较大的英文译本[1- 3]。G.Thibaut和M.S.Dvivedi的英译本出版于1889年,该译本对部分术文没有翻译,并且除了译文没有注释和说明。D.Pingree的英译本于1970年出版,与G.Thibaut和M.S.Dvivedi的英译本相比,D.Pingree的英译本内容相对比较完整,并且作为姊妹篇,D.Pingree和O.Neugebauer合作出版了专门研究《五大历数全书汇编》的著作[4]。T.S.Kuppanna Sastry的英译本于1993年出版,尽管该译本有许多印刷错误,但它纠正了前两个译本的许多错误,并附有非常详细的注释说明及算例。上述三个英译本在释读某些术文时,还存在较大的分歧,但总体来说,T.S.Kuppanna Sastry的英译本相对较好。本文的讨论主要基于T.S.Kuppanna Sastry的英译本,同时参考了另外两个英译本。基于上述三个英译本,科学史家对《五大历数全书汇编》中的太阳运动理论、月球运动理论和行星理论都有较为系统的研究[5- 9]。

全面研究《五大历数全书汇编》,不仅对我们全面了解早期印度数理天文学的基本思想、方法与精度具有重要的意义,而且对我们探讨巴比伦和希腊天文学在印度的流传与影响以及印度对域外天文学的接纳程度具有重要意义。此外,通过对《五大历数全书汇编》的研究,还有助于我们开展早期中印数理天文学比较,并探讨中印天文学交流与传播的痕迹。

在《五大历数全书汇编》收录的五部著作中,只有《太阳历数书》、《宝莉莎历数书》和《沃西斯特历数书》三部著作讨论了行星理论。这三部著作中的行星理论分为两个系统,《太阳历数书》中的行星运动理论采用“双本轮模型”,以三角函数作为主要计算工具,来推求任意时刻行星的位置,属于印度行星理论的主流传统；而《宝莉莎历数书》和《沃西斯特历数书》则完全使用代数方法计算行星的位置,其中行星在一个会合周期内的动态表,以及利用相减相乘算法计算行星中心差修正算法的方法,在印度其他数理天文学著作中都非常少见。按照《五大历数全书汇编》的编排方式,被收录的五部著作并不是完全独立的,各部著作中内容相同的章节通常放在一起叙述,例如《宝莉莎历数书》和《沃西斯特历数书》中的行星理论就是放在一起讨论的,并且数据及算法完全相同。因此为叙述方便,在下面的讨论中,我们仅以《宝莉莎历数书》为例,而不再提及《沃西斯特历数书》。

在《宝莉莎历数书》中,最先讨论的是金星,然后是木星、土星、火星和水星,这个顺序基本上是按照计算难易程度来排序的。这五个行星的处理方法也不相同,金星计算由于未涉及中心差而比较简单；木星和土星的处理方式相同,都是先根据行星动态表计算行星的平位置,然后考虑行星中心差修正；而火星和水星的五星动态表与中心差混杂在一起,计算最为复杂。本文试图对《宝莉莎历数书》中的五星动态表、中心差修正算法以及黄经计算精度进行初步探讨。由于现有的英译本对水星动态表的解读尚不完整,因此本文的讨论不包含水星。

1 行星始见时刻及位置

《宝莉莎历数书》中行星理论的核心目的,是推算任意时刻行星的黄经。与印度其他数理天文学著作一样,《宝莉莎历数书》将“始见”作为行星会合周期的起点,推算行星始见时刻及位置是行星运动理论中的第一个算法。印度历法一般取近距历元,《宝莉莎历数书》所取近距历元为释迦427年制呾逻月(Caitra)白半一日亚历山大日落时分,换算成公历为公元505年3月20日。*释迦纪年为古代印度的一种纪年方法,释迦元年为公元78年,故释迦427年即为公元505年。制呾逻月(Caitra)为印度历一月,相当于公历三月。古代印度将一个朔望月分为两半,其中月盈到满称为白分,又叫白半或白博叉,月亏到晦叫黑分,又叫黑半或黑博叉。《五大历数书汇编》在第15章([3],288页)讨论日界问题时指出,天文学家根据不同的习惯对日界的选择不同,日落、夜半和日出都可作为一日的开始。《宝莉莎历数书》以日落作为日界,公元505年3月20日日落即为3月21日开始,按3月21日为礼拜一,符合《宝莉莎历数书》所称历元从礼拜一起算,因此《宝莉莎历数书》所取历元应为公元505年3月20日亚历山大城日落时分。文献[3]在讨论水星运动时,明确指出《宝莉莎历数书》所取历元为505年3月20日([3],341页)。

1.1 金星始见算法

若已知历元以来积日和行星的会合周期,则行星在历元后始见的次数和行星在会合周期内的位置即可求出。以金星为例,其术文称：

置历元以来积日,减去174,余数除以584,所得商数即为金星偕日升的次数。它在每个周期内运行7r5°30′20″。

当金星运行至处女宫26°,亦即5宫26°时,从西方升起。将商数的1/11,加到剩余的日数内,其运动(可从3- 5节所给表中求出)。([3],312页)

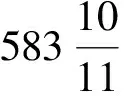
1.2 木星和土星始见算法

《宝莉莎历数书》计算木星始见的方法与金星略有不同,其术文称：

置历元以来积日,减去34日34nādikās,除以399,得到偕日升的次数,余数为(始见后的)日数。

剩余的日数加偕日升次数的1/9。偕日升的次数乘以36,加上18,除以391,余数的单位为padas。([3],316页)

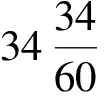
术文中的pada是《宝莉莎历数书》中的一个技术名词。古代巴比伦天文学家主要依据以下关系来处理行星的周期运动：427个恒星年内，木星与太阳会合391次，同时木星绕黄道36圈；265个恒星年内，土星与太阳会合256次，同时土星绕黄道9圈；284个恒星年内，火星与太阳会合133次，同时火星绕黄道151圈。[10]《宝莉莎历数书》采用了完全相同的关系来处理行星运动。按木星在391个会合周期内绕黄道36圈，则它在一个会合周期内绕黄道36/391圈。因此《宝莉莎历数书》将黄道一周分为391padas，木星在一个会合周期内运行36padas，转化为相应的黄经增量为360°×36/391。

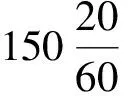
1.3 火星始见算法

《宝莉莎历数书》计算火星晨始见算法称：

置历元以来积日,减去256;40,除以780,即为火星晨见次数。

用161vinādis乘以晨见次数,加上剩余的日数。晨见次数乘以18,加上85,除以133,将所得余数转化为黄道十二宫,即得到火星始见时的位置。按照整宫或不满整宫的度数,可相继求出火星的真位置。([3],328～329页)

《宝莉莎历数书》认为，火星在133个会合周期内绕黄道151圈，则在一个会合周期内绕黄道151/133圈。为计算方便，《宝莉莎历数书》将黄道一周分为133padas，火星在一个会合周期内运行151padas，则火星在一个会合周期内黄经增量为151-133=18padas，又根据术文，历元后火星第一次始见时的黄经为85padas，因此火星在历元后第m+1次始见时的黄经为360°×(m×18+85)/133。类似地，若(m×18+85)>133，则需从(m×18+85)中减去133的整数倍再将其换算为相应的黄经。

2 行星动态表

如果不考虑行星和太阳的不均匀运动，则行星在一个会合周期内的运动是有规律的。将行星在一个会合周期内的运动划分为若干段目，用来刻画行星的顺、逆、迟、疾运动，这是《宝莉莎历数书》处理行星平运动的基本思路。五星动态表是中国古代行星理论中必备的天文表格，但古代印度的数理天文学著作中，除《宝莉莎历数书》和《沃西斯特历数书》这两部采用代数方法计算行星运动的著作设计了类似的五星动态表以外，其他根据本轮模型计算行星运动的著作都未设计类似的动态表。

《宝莉莎历数书》将金星、木星和土星在一个会合周期内的运动分为若干段目，并给出了行星在每个段目内运行的时间和距离。金星动态表从夕始见开始，到晨伏行结束，共17个段目，其中11个段目顺行，6个段目退行，且从上合到下合与从下合到上合的运行状态呈镜面对称。木星和土星的动态表均从晨见开始，伏行结束，共8个段目，其中6个段目顺行，2个段目退行。

曲安京在讨论中国古代行星理论时[11]，曾用几何方法构建了五星动态表的数学模型。唐泉在讨论中国古代五星动态表中“留”与“退”这两个段目的精度时[12]，从运动学的角度推出了入平合度β与入平合日t之间的关系，若令r表示行星的轨道半长径，vp和ve分别表示行星和地球绕太阳公转的平均角速度，x=rcos(vpt)+cos(vet)和y=rsin(vpt)+sin(vet)分别表示行星在以地球为原点，平合方向为x轴正向的直角坐标系中的横坐标和纵坐标，则入平合度β可以表示为

(1)

利用式(1)，可以讨论《宝莉莎历数书》金星、木星和土星动态表的误差。由于《宝莉莎历数书》中金星、木星和土星动态表均以始见作为会合周期的起点，而式(1)给出的数学模型是从“合”起算的，为讨论方便，我们将金星夕始见和木星与土星晨始见之前伏行时间和度数分别平分，即可得到从“合”开始的行星动态表。其中木星和土星的动态表从合开始，金星的动态表从上合开始，根据对称性，我们仅给出金星从上合到下合的动态表，另一半完全对称。

在计算理论结果时，我们取金星、木星和土星的轨道半长径分别为0.723、5.205和9.576天文单位，公转周期分别为224.701、4332.589和10759.2日，地球的公转周期为365.256日。[13]令Δt表示“常日”，意为行星在各段目内的运行时间，t表示“入平合日”，亦即“常日”的累加值；ω和ω′分别表示“常度”的历法结果和理论结果，意为行星在各段目内的视位移，β和β′分别表示“入平合度”的历法结果和理论结果，其值分别为ω和ω′的累加值。我们将计算所得结果列为表1～表3，表中第2列“常日”Δt与第4列“常度”ω数据取自《宝莉莎历数书》，第3列“入平合日”t由第2列“常日”Δt累加得到，第7列“入平合度”的历法结果β由第4列“常度”ω累加得到，第5列ω′和第8列β′数据系笔者根据式(1)计算所得，其中β′为ω′的累加值。Δω=ω-ω′表示“常度”误差，Δβ=β-β′表示“入平合度”误差。表1～表3中，Δt和t的单位为“日”，ω、ω′、Δω、β、β′和Δβ的单位为“°”。

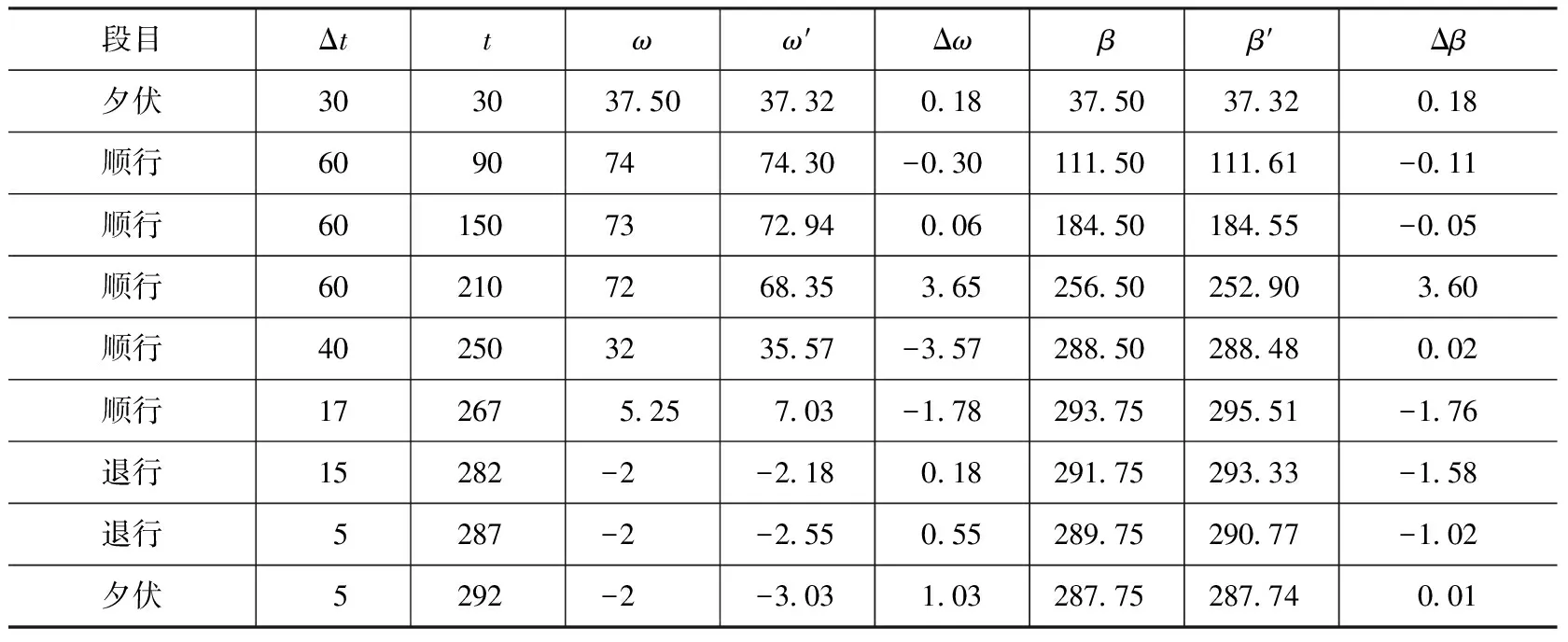
表1 金星动态表精度

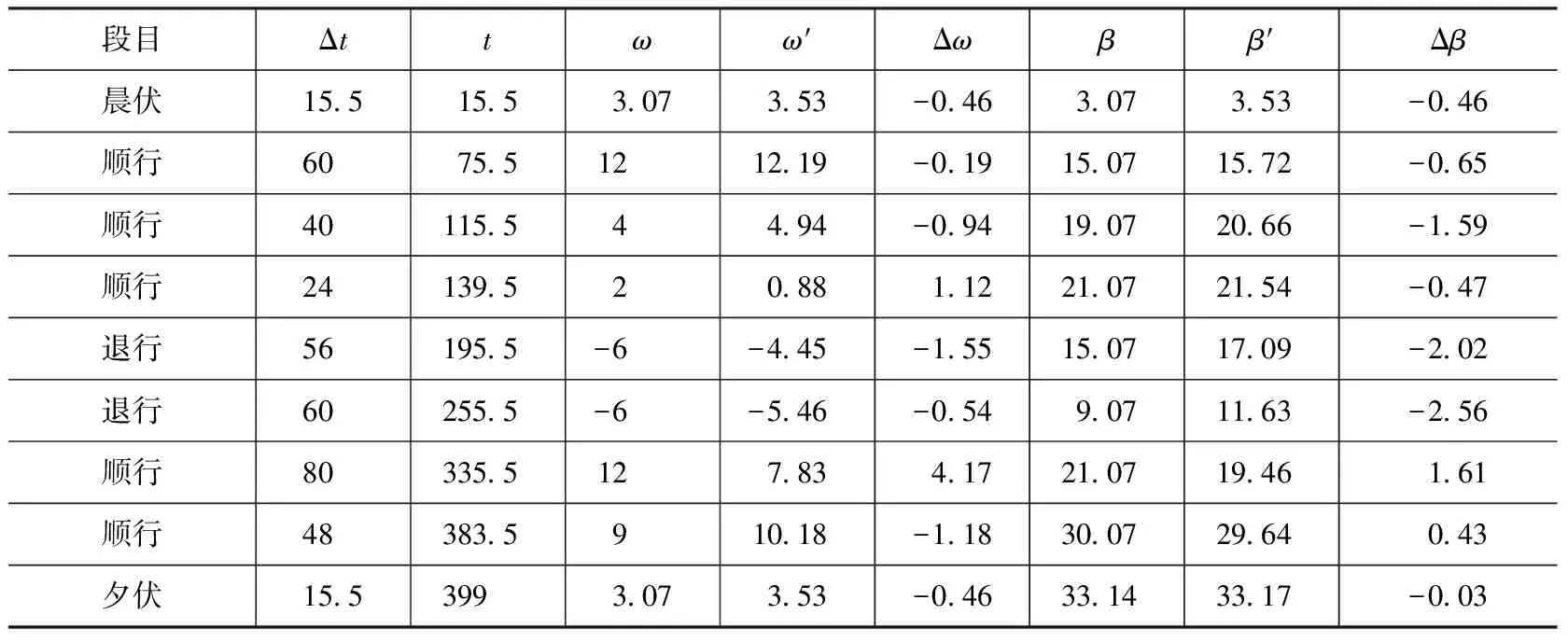
表2 木星动态表精度

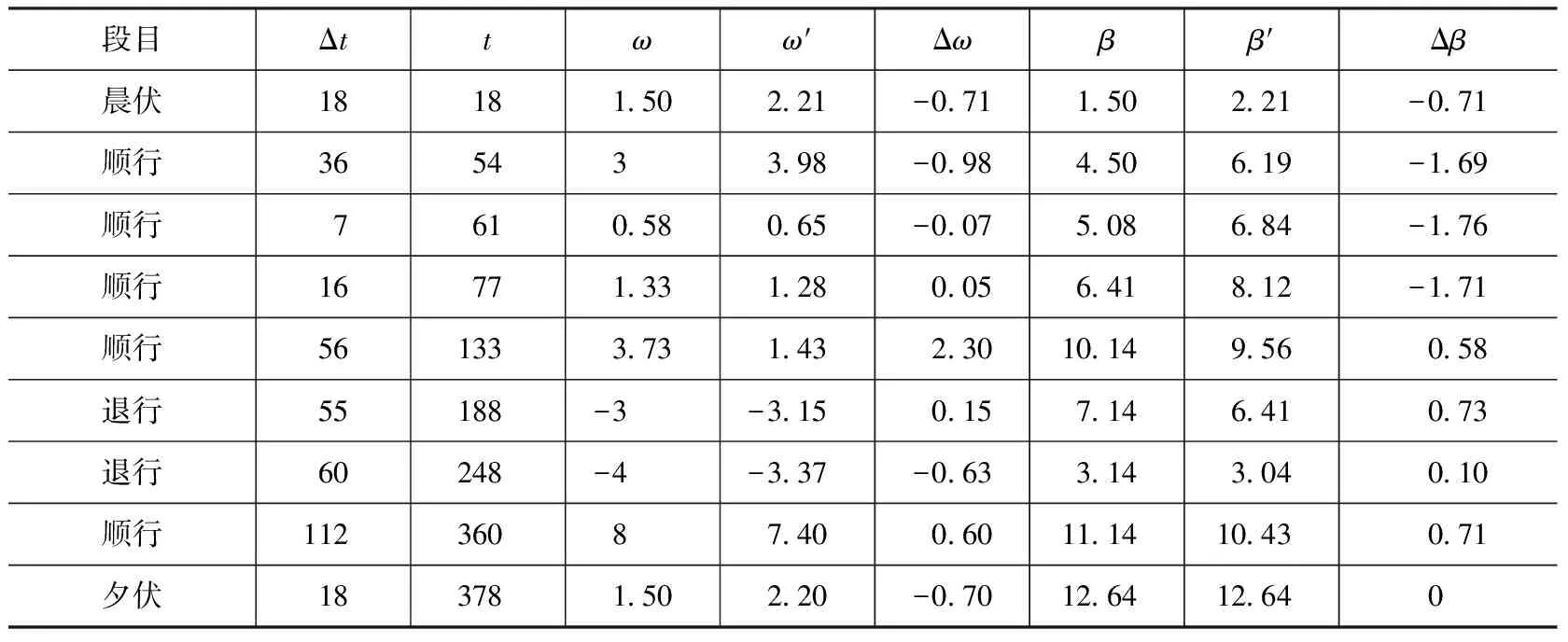
表3 土星动态表精度

从表1～表3可以看出，金星、木星和土星各段目常度绝对误差的最大值分别为3.65°、4.17°和2.30°。由于行星的入平合度是各段目常度的累加值，而各段目常度的误差可正可负，因此入平合度的误差与常度的误差一般并不同步，也就是说，常度误差最大时，对应的入平合度误差并非最大，反之亦然。表1～表3中的数据表明，金星、木星和土星入平合度的绝对误差的最大值分别为3.60°、2.56°和1.76°，分别小于相应常度的最大误差。由于行星动态表是计算行星平位置的基础，因此金星、木星和土星入平合度的误差较好地反映了《宝莉莎历数书》金星、木星和土星平位置计算精度。

《宝莉莎历数书》设计火星动态表的思路与金星、木星和土星不同。金星、木星和土星动态表中，行星在各段目内运行的时间和视位移是固定的。《宝莉莎历数书》将火星在一个会合周期内的运动分为8个段目，火星在各段目内的视位移分别为：“疾行”(146°)、“迟行”(18°)、“迟退”(18°)、“疾退”(18°)、“迟顺”(18°)、“疾顺”(150°)、“合前伏顺”(60日内运行43°)、“合后伏顺”(60日内运行43°)。火星在各段目上的视位移虽然确定，但火星在各段目内的速度则根据火星的黄经而变化，从而导致火星在各段目内运行的时间并非常数。火星在各段目内的速度随黄经变化(表4)。表4中数据单位均为“°/日”。

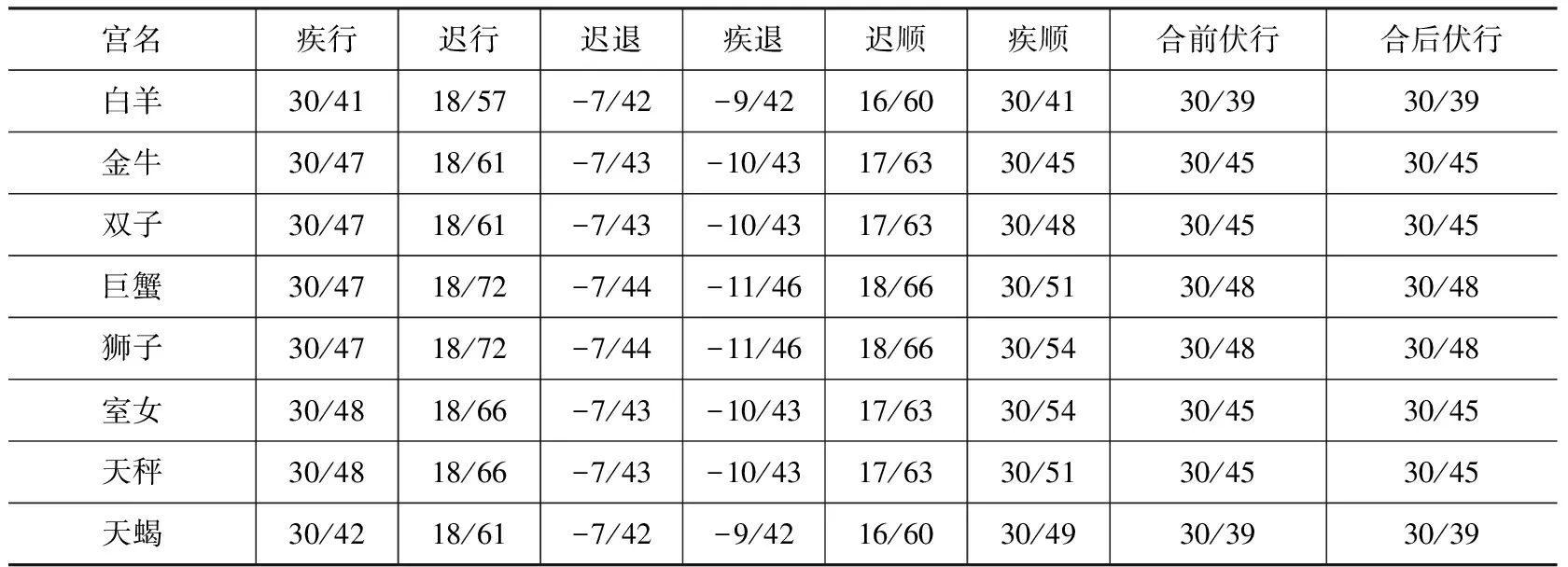
表4 火星在各段目内的视行速

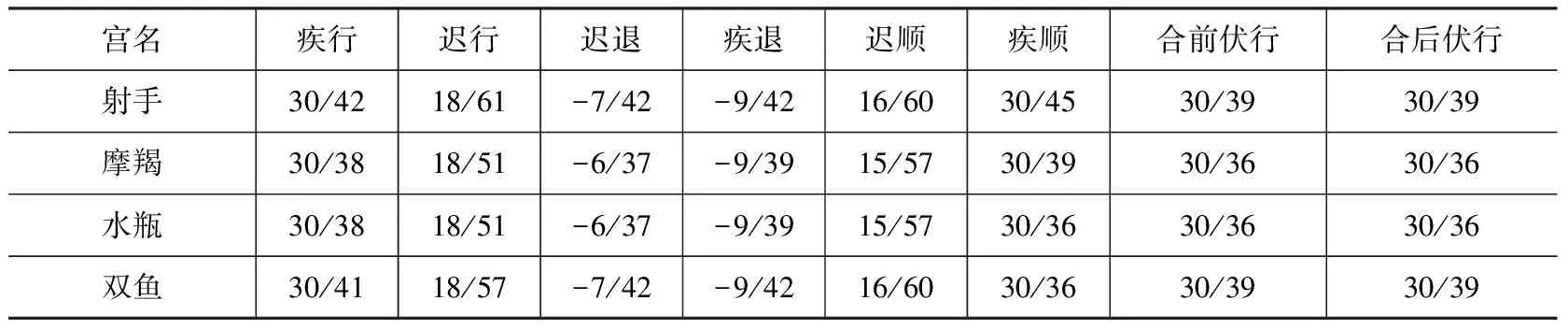
续表4

从表4中的数据可以看到，当火星运行在除“疾顺”外的其他7个段目内时，其速度根据它在黄道十二宫中的位置分为6组，若用vi表示火星在第i宫中的速度，则有：v1=v12，v2=v3，v4=v5，v6=v7，v8=v9，v10=v11，这个关系对“疾顺”段并不满足。

此外，根据《宝莉莎历数书》术文，当火星在“迟退”、“疾退”、“迟顺”、“合前伏行”和“合后伏行”这五个段目内运行时，其视位移与表4中所给数据并不完全吻合。例如，当火星在表4中“迟退”、“疾退”和“迟顺”这三个段目内运行时，其运行时间和视位移均由火星黄经所决定，以火星逆行在白羊宫内为例，其运行状态如下：42天内逆行7°，42天内逆行9°，然后在60天内顺行16°，其逆行和顺行的度距均为16°，而非18°；当火星运行在“合前伏顺”和“合后伏顺”两个段目内时，由于火星运行的速度随黄经而变化，因此火星运行43°的时间也并不一定等于60天。

显然，与金星、木星和土星不同，火星动态表实际上已经考虑了火星中心差影响，因此不能用式(1)讨论火星动态表的精度。

3 行星位置计算的基本思路

行星中心差修正算法是《宝莉莎历数书》行星理论中的核心算法。由于金星中心差较小，《宝莉莎历数书》在讨论金星运动时忽略了中心差，金星在任意时刻的黄经由其始见时的黄经以及动态表即可求出。但是，木星、土星和火星计算都涉及中心差修正算法，因此计算比较复杂。计算木星和土星黄经的方法完全相同，以木星为例，其基本思路可以概括为如下四个步骤：

(1)计算木星在历元后某次始见时的平位置λ0；

(2)计算木星始见x日后与中心差相关的变量cp；

(3)根据木星动态表，求出木星在平见后x-cp日内的视位移λ(x-cp)；

(4)求出木星地心真黄经λ=λ0+λ(x-cp)+cp。

根据《宝莉莎历数书》木星始见算法，木星于历元后首次始见时的位置为18padas，木星在一个会合周期内运行36padas，因此木星于历元后第m+1次始见时的黄经为(m×36+18)×360°/391，若m×36+18>391，则需从m×36+18中减去391的整数倍后再将其换算为相应的黄经。

在上述四个步骤中，第二个步骤——即计算cp——最为关键。cp是《宝莉莎历数书》设计的一个与行星中心差有关的函数，其值为

cp=λt-λm

(2)

(3)

λm中的p和式(3)中的p均代表padas。《宝莉莎历数书》将木星在一个恒星周期(391padas)内的运动分为三段，分别为(0～180)、(181～375)和(376～391)，其中第一段和第三段称为减速段，对应木星从近日点到远日点的运动，第二段称为加速段，对应木星从远日点到近日点的运动。

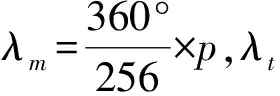
(4)

显然，根据《宝莉莎历数书》所给算法求出的cp，并非现代天文学意义上的中心差，而是为修正中心差而设计的一个函数。从cp对木星和土星黄经计算的影响效果来看，其涵义和功能与中国古代行星理论中的五星盈缩差算法非常类似。关于中国古代五星盈缩差算法的天文意义与数学模型，唐泉有比较详细的论述[14〗。

为了考察cp对木星和土星黄经计算误差的影响，我们从木星和土星的减速段起点开始，以30°为间隔，分别计算出木星和土星在一个恒星周期内的12组cp值，结果如表5所示。

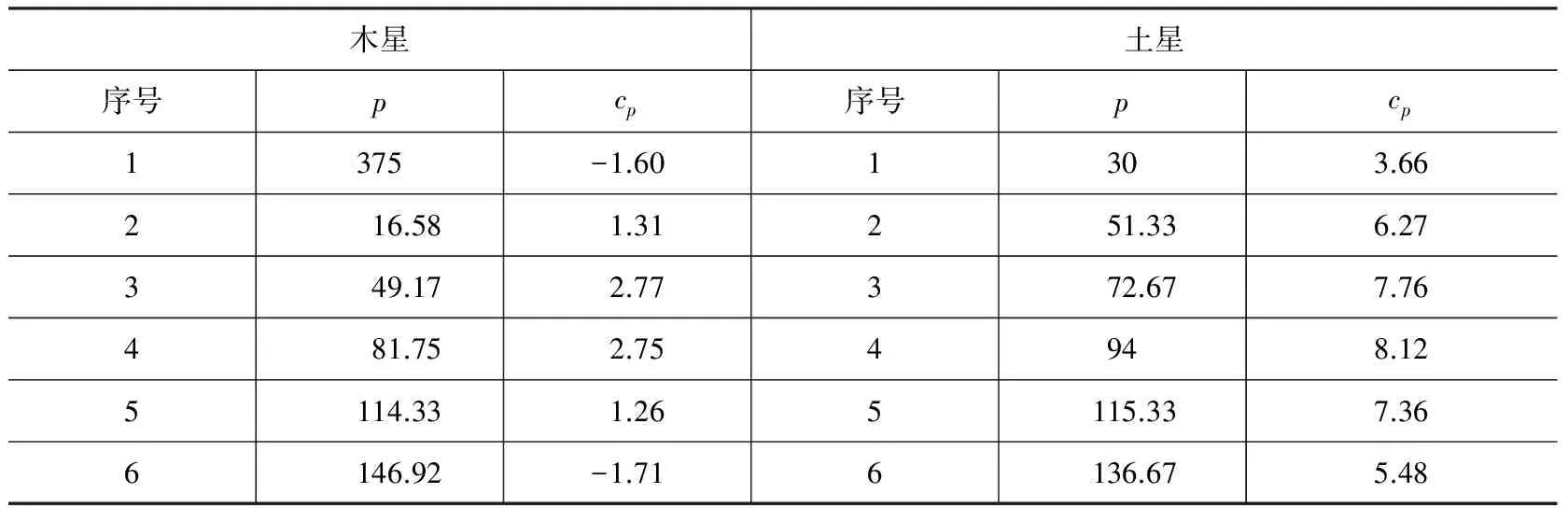
表5 木星和土星的cp

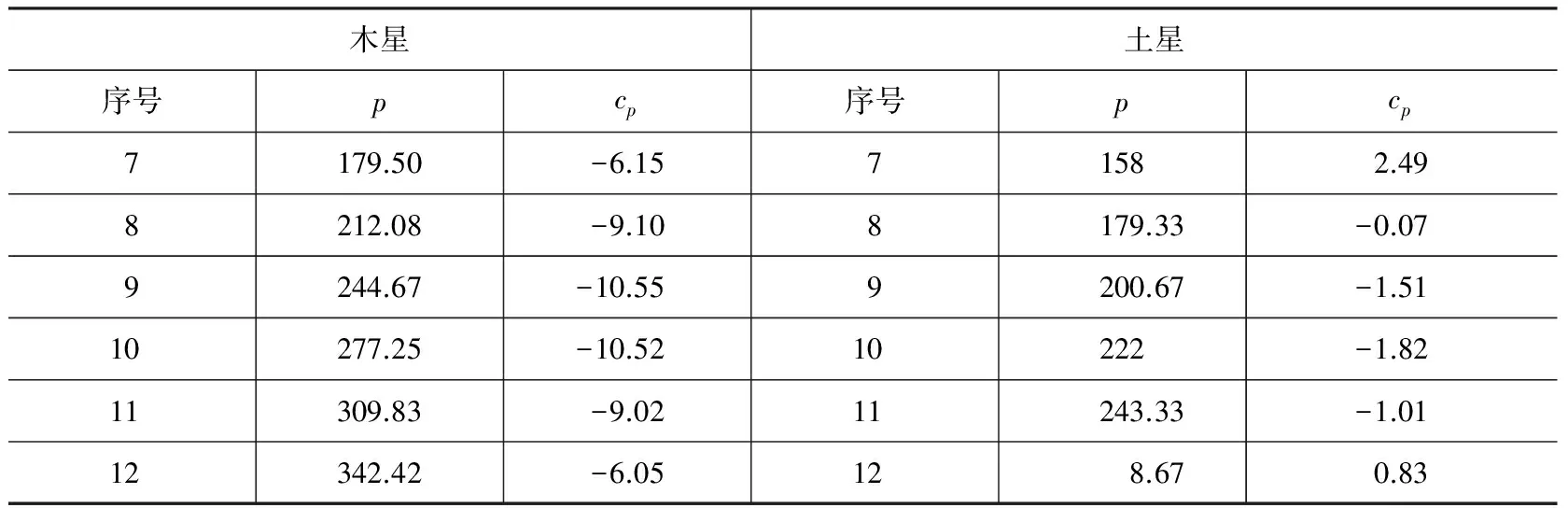
续表5

表5中的数据表明，木星和土星的中心差修正函数cp的曲线形状均接近正弦函数曲线，不过与标准的正弦函数曲线位置相比，木星的cp曲线沿y轴约下移3°左右，而土星的cp曲线沿y轴约上移3°左右。在后面的讨论中我们将会看到，对木星和土星而言，与中心差有关的修正项cp对其黄经计算误差的影响是非常明显的。

在《宝莉莎历数书》中，计算火星黄经的算法与金星、木星和土星都有所不同。根据火星始见算法以及火星动态表，即可求出火星在某次晨见后x日的黄经λ(x)。根据《宝莉莎历数书》火星算法，以上述方法求出火星黄经λ(x)后，还要对其进行修正，该修正算法称：

若平位置大于真位置，则将二者之差加入“所得余数”；若平位置小于真位置，则需从“所得余数”中减去二者之差；做完这些，我将根据(火星)每段运动给出(火星)真运动。([3]，328～329页)

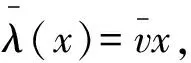
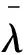
4 行星黄经计算精度

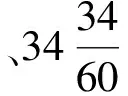
讨论行星黄经的计算精度，首先需要一份高精度的行星历表。本文采用天文软件Skymap Pro 10*关于Skymap的精度，已有学者进行过专门讨论。江晓原和钮卫星在讨论武王伐纣的年代和日程表时，曾用DE系列的星历表DE404检验了Skymap Pro 3.2的精度，发现在前推3000余年时，其误差也仅在角秒量级。(江晓原、钮卫星：《以天文学方法重现武王伐纣之年代及日程表》，《科学》，1999年5期)。宁晓玉和刘次沅用一些专业天文软件，如DE系列、Sumer、LUNE等，检验了包括Skymap Pro 7和Skymap Pro 3.2在内的一些商业天文软件的精度，认为Skymap与专业历表软件的外行星位置符合相当好，内行星位置在远距历元处有0.1°以内的误差，因此无论从数据精确度和长期稳定性，还是从功能的强大程度来说，Skymap都是值得推广的天文计算软件，并建议选择Skymap作为古天文研究的主要参考软件。(宁晓玉、刘次沅：《适用于古天文研究的计算机软件》，《时间频率学报》，2006年1期)来获取行星位置的理论结果。需要说明，由于Skymap Pro 10只提供行星的赤经和赤纬而无黄经和黄纬，因此本文在计算行星的理论黄经时，首先由Skymap Pro 10获取行星的赤经和赤纬，然后再将赤经转化为黄经。

作为例子，我们计算公元505年10月1日夜半木星的黄经及其误差。由前面讨论知，《宝莉莎历数书》所取近距历元公元505年3月20日亚历山大城的日落时分，该日对应的儒略日序为1905588，木星在505年4月24日19nādikās始见，对应儒略日序为1905623，505年10月1日对应儒略日序为1905783。下面给出具体计算步骤：

(1)计算木星始见时的黄经λ0。由术文，λ0=18×360°/391=16.57°。

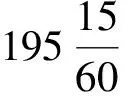
(3)根据木星动态表，计算木星在平见后x-cp日内的视位移λ(x-cp)。x-cp=160.68-1.99=158.69。根据木星动态表(表2)，可求出木星始见后158.69日的视位移λ(158.69)=18°+(158.69-124)/56×(-6°)=14.28°。

(4)计算木星在505年10月1日夜半时的黄经λ。根据《宝莉莎历数书》计算木星黄经的思路，λ=λ0+λ(x-cp)+cp=16.57°+14.28°+1.99°=32.84°。

(5)计算505年10月1日夜半木星黄经的理论值λ′。查亚历山大经度为东经29°55′，属东二区，该地地方时比世界时早2小时。使用Skymap Pro10查得505年10月1日22时木星的赤经为2h 4m 45.39s，赤纬为+11°15′01.7″，按公元505年黄赤夹角为23.63°，转化为相应的黄经为λ′=32.94°。

(6)计算505年10月1日夜半木星黄经误差Δλ。Δλ=λ-λ′=32.84°-32.94°=-0.10°。

为充分考察中心差对行星黄经计算精度的影响，我们根据《宝莉莎历数书》术文，用Matlab语言将金星、木星、土星和火星黄经计算全部程序化。我们从历元后首次始见当天夜半开始，共计算了金星、木星和土星在11000*金星、木星和土星的公转周期分别为224.701、4332.589、10759.2日，本文在计算金星、木星和土星的黄经时，所选时间跨度均为11000日，其数值非常接近土星公转周期。日内每日夜半的地心黄经，并与理论结果进行比较。由于火星在各段目内运行的时间和距离均与黄经有关，计算较为复杂，且火星的公转周期较短，因此我们只计算了火星在一个会合周期(780日)内每天夜半的黄经，并与理论结果进行比较。由于已有的三个英译本对火星中心差修正算法解读存在较大分歧，且该算法的意义不太明确，因此在计算火星黄经时，未考虑中心差修正算法。我们对计算结果进行误差分析，结果如表6所示。表6中的数据比较客观地反映了《宝莉莎历数书》中的行星计算精度。

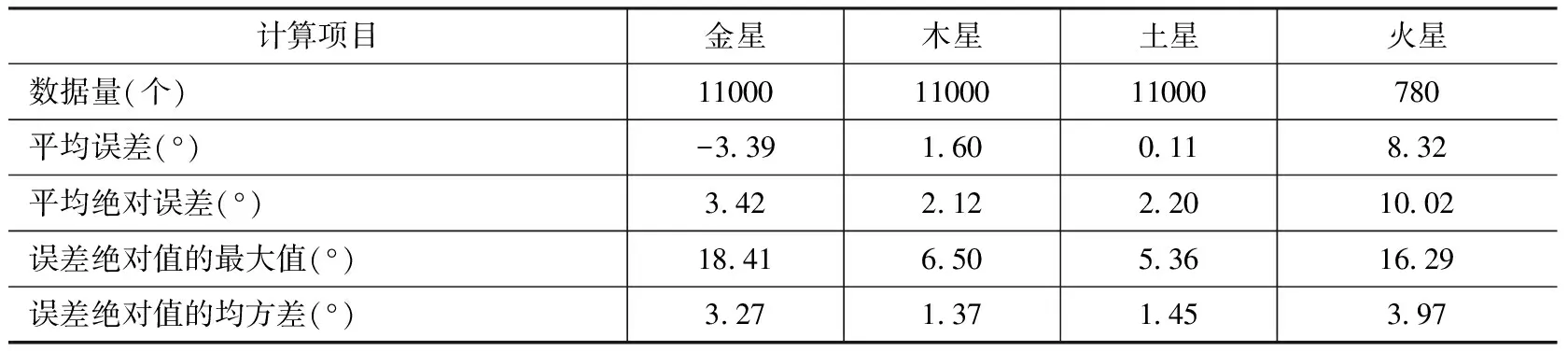
表6 《宝莉莎历数书》行星计算精度

为了更直观地考察《宝莉莎历数书》中的行星计算精度，我们根据计算结果分别绘出金星、木星、土星和火星的黄经误差散点图(图1～图4)。图1～图4中纵坐标表示行星黄经绝对误差(历法值-理论值)，单位为“°”，横坐标表示行星从历元后首次始见当日夜半起算的日数，单位为“日”。根据前面对行星始见时刻的讨论，图1中横坐标始于505年9月10日夜半，图2中横坐标始于505年4月24日夜半，图3中横坐标始于505年8月18日夜半，图4中横坐标始于505年12月2日夜半。

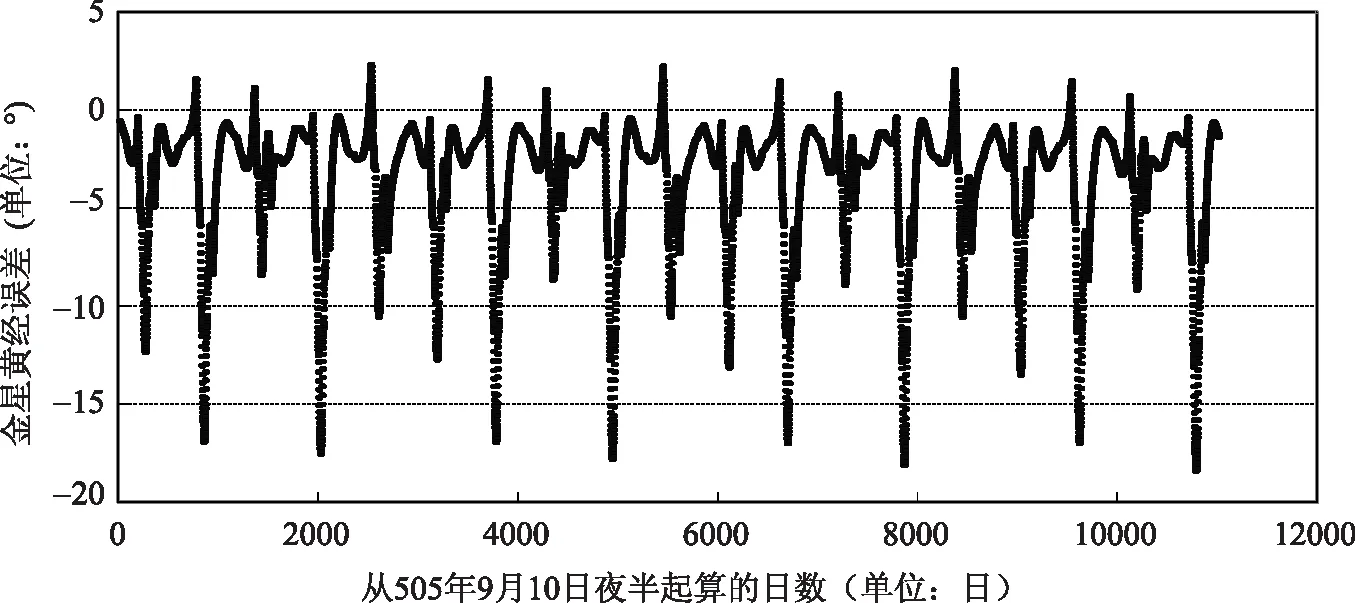
图1 金星黄经绝对误差散点图

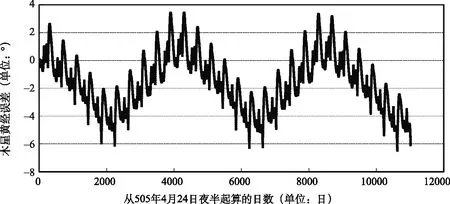
图2 木星黄经绝对误差散点图

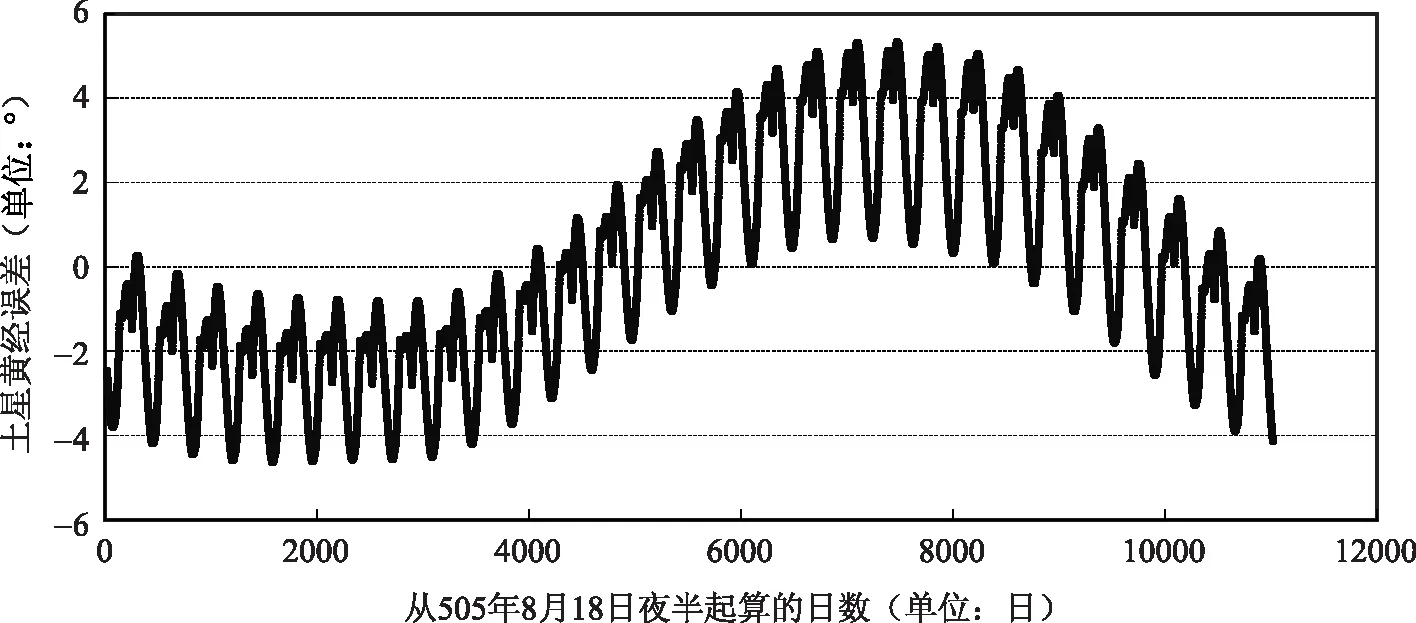
图3 土星黄经绝对误差散点图

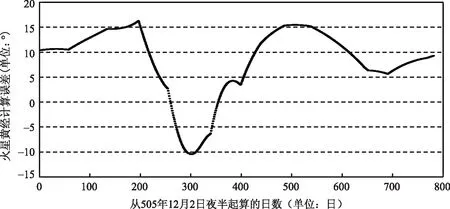
图4 火星黄经绝对误差散点图

从图1～图4可以看出，木星和土星黄经计算精度大体相当，其中木星和土星黄经计算误差基本能控制在6°以内，只在极少数点，木星黄经计算误差超过6°。金星和火星黄经计算精度大体相当，其最大误差均超过了15°，且金星黄经有明显的后天现象，而火星黄经有明显的先天现象。此外，从图2可以看出，由于行星的近点周期运动，木星误差曲线的波动周期与其公转周期基本吻合，不过对于金星、土星和火星，看不到类似的波动曲线，因为我们考察土星和火星黄经计算精度时，其时间跨度分别接近各自的公转周期，而金星的公转周期较小，又未考虑中心差。

为了考察《宝莉莎历数书》中木星和土星中心差修正算法效果，我们仅仅根据木星和土星动态表，而不考虑中心差修正算法，得到木星和土星黄经计算误差散点图(图5～图6)。

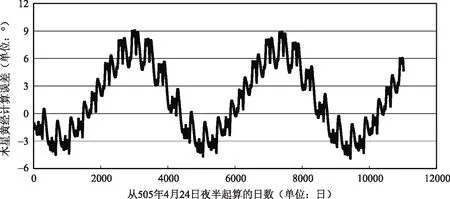
图5 木星黄经绝对误差散点图(不考虑中心差)

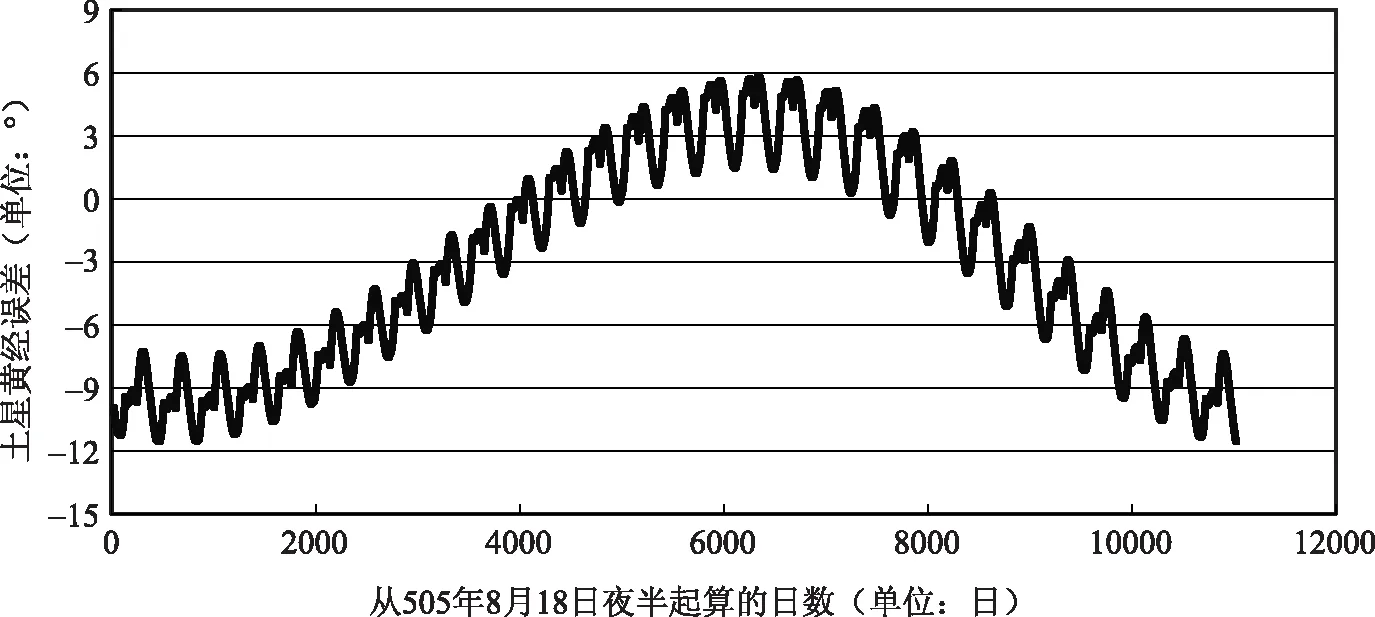
图6 土星黄经绝对误差散点图(不考虑中心差)

从图5和图6可以看出，如果不考虑中心差，则木星黄经的最大误差达到了9°左右，土星黄经的最大误差达到了12°左右，其精度明显低于考虑中心差时的情形，这说明木星和土星中心差修正算法的效果还是比较明显的。另外，从图5和图6也容易看出，木星黄经先天现象严重，而土星黄经后天现象严重。但是前面的讨论表明，木星和土星的中心差修正函数cp的曲线形状均接近正弦函数曲线，但与标准的正弦函数曲线位置相比，木星中心差修正曲线大约沿y轴下移3°左右，而土星曲线沿y轴约上移3°左右。正是因为这个原因，图2和图3中木星和土星的黄经并未出现特别明显的先天或后天现象。

5 分析及结论

本文对《宝莉莎历数书》中金星、木星、土星和火星的动态表、中心差修正算法和黄经计算方法及精度进行了初步讨论。根据前面的讨论，我们可以得出如下一些结论：

(1)根据表6中的数据，《宝莉莎历数书》中木星和土星黄经最大误差分别为6.50°和5.36°，木星和土星黄经平均绝对误差分别为2.12°和2.20°，这表明《宝莉莎历数书》中木星和土星的计算精度大体相当。与木星和土星相比，火星和金星黄经计算误差则要大得多。金星和火星黄经最大误差分别为18.41°和16.29°，约为木星和土星黄经最大误差的3倍。金星和火星黄经最大误差虽然相差不大，但是金星和火星黄经平均绝对误差分别为3.42°和10.02°，这表明金星黄经计算误差要明显小于火星黄经计算误差。另外，当金星、木星、土星和火星分别运行至各自的会合周期中逆行段目前后时，黄经计算误差最大。对古代天文学家而言，由于内行星不易观测且其速度较快，故计算难度较大，而火星在三个外行星中轨道偏心率最大，计算也明显比木星和土星复杂。《宝莉莎历数书》中的行星计算精度，较为真实地反映了各个行星的计算难度。

(2)行星动态表是影响《宝莉莎历数书》行星计算精度的一个主要因素。行星动态表是《宝莉莎历数书》计算行星平位置的基础，因此行星动态表设计是否合理会直接影响行星计算精度。根据《宝莉莎历数书》行星始见算法，可以求出金星、木星、土星和火星的会合周期分别为583.91、398.89、378.10和779.96日，与之相应的理论结果分别为583.92、398.88、378.09和779.94日，绝对误差取整至分钟分别为-14、14、14和29分钟，其精度明显高于中国隋代《开皇历》(584)及其以前诸历对五星会合周期的测定，即使与唐代《麟德历》等历法测定的五星会合周期相比，也豪不逊色。另外，根据现代天文学理论，行星在各段目内的速度是逐日变化的，而《宝莉莎历数书》设计的行星动态表中，行星在各段目内匀速运行，而造成行星速度在各段目节点处会发生较大跳跃。根据表1～表3，金星、木星和土星入平合度的最大误差分别为3.60°、2.56°和1.76°，金星误差明显高于木星和土星，其原因在于金星会合周期较长且作为内行星不易观测。金星、木星和土星入平合度的误差较好地反映了《宝莉莎历数书》金星、木星和土星平位置计算精度。

(3)行星中心差修正算法是影响《宝莉莎历数书》行星计算精度的另外一个主要因素。金星的入平合度的最大误差虽然只有3.60°，但是由于《宝莉莎历数书》在计算金星黄经时并未考虑中心差，从而使得金星黄经计算误差急剧增大，最大误差甚至超过了18°。尽管木星和土星中心差修正函数的设计还存在一些缺陷，但是通过对木星和土星黄经计算误差的讨论，我们发现木星和土星的中心差修正算法确实有效提高了木星和土星的黄经计算精度。《宝莉莎历数书》将火星动态表与行星的黄经相联系，实际上是将火星的动态表与中心差混合在一起，其做法与隋代及初唐时期历法中的火星动态表的设计非常类似。由于已有的英译本在解读火星中心差修正算法时，还存在很大分歧，故火星中心差修正算法的天文涵义还有待深入研究。

(4)造成火星黄经计算误差较大的原因，主要有以下几点：其一，在计算火星黄经时，并未考虑火星中心差修正算法；其二，火星在历元后首次始见当日夜半黄经的理论结果为220.07°，而根据《宝莉莎历数书》计算结果为230.49°，二者之间有10°左右的误差；其三，《宝莉莎历数书》设计的动态表中，火星在一个会合周期内运行400°，相应的理论结果为408.72°，其误差为8.72°。另外，从图4可以看到，如果不考虑火星的中心差修正算法，则火星的黄经计算误差能控制在17°以内。作为对照，我们按照文献[3]对火星中心差修正算法的解读，重新计算了火星在一个会合周期内的黄经误差，结果表明，火星中心差修正算法不仅未提高火星黄经计算精度，反而使火星黄经计算精度大幅度降低，其最大误差达到了36.21°。这或许说明，文献[3]对火星中心差修正算法的解读可能有误。

与早期印度一些影响较大的数理天文学著作，如《阿耶波多历数书》(5世纪)、《历法甘露》(7世纪)和《苏利亚历》(公元8、9世纪)等著作采用本轮模型计算行星位置的主流传统相比，《宝莉莎历数书》行星理论中强烈的代数传统显得格外引人注目。事实上，《宝莉莎历数书》中的行星理论虽然与印度主流行星理论传统不同，但却与古代巴比伦和中国行星理论传统非常相似。如果对《宝莉莎历数书》和隋唐时期中国历法中的行星理论进行比较，不难发现二者确实有许多相似之处。例如，二者均采取分段处理方案来设计行星在一个会合周期内的运动；在设计火星动态表时，二者均将火星动态表与火星中心差混杂在一起。[15]江晓原[16]认为在公元6世纪前后，巴比伦天文学——特别是太阳理论和行星理论方面——很可能通过某种途径对中国天文学产生过影响，那么，印度天文学是否在巴比伦天文学影响中国天文学的过程中，扮演了一个重要角色呢？这个问题仍然值得深入研究。

致谢两位审稿专家指出了本文的一些疏漏之处,并提出了宝贵的修改意见。在本文的修改过程中,作者曾与日本大桥由纪夫博士进行了有益的讨论。在此一并表示诚挚的感谢!

5 Abraham G. The motion of the Sun in the Vsisa Siddhnta[J].ArchiveforHistoryofExactScience, 1980, 22(1～2): 1～3.

6 Abraham G. Algebraic Formulae for the Moon, Saturn and Jupiter in the Pacasiddhntik[J].ArchiveforHistoryofExactSciences, 1982, 26(4): 287～297.

7 Abraham G. Length of the Year in Pre-epicyclic Planetary Theory[J].ArchiveforHistoryofExactSciences, 1984, 30(3～4): 189～195.

8 Abraham G. Theories for the Motion of the Sun in the Pacasiddhntik[J].ArchiveforHistoryofExactSciences, 1985, 34(3): 221～230.

9 Waerden B L V. On the Romaka-Siddhnta[J].ArchiveforHistoryofExactSciences, 1988, 38(1): 1～11.

10 江晓原, 钮卫星. 天文西学东渐集[M]. 上海：上海书店出版社, 2001. 51.

11 曲安京. 中国古代的行星运动理论[J]. 自然科学史研究, 2006, 25(1): 1～17.

12 唐泉. 中国古代五星动态表的精度——以“留”与“退”两个段目为例[J]. 内蒙古师范大学学报(自然科学汉文版), 2013, 42(4): 463～470.

13 中国大百科全书出版社编辑部. 中国大百科全书·天文学卷[M]. 北京: 中国大百科全书出版社, 1980. 477.

14 唐泉. 再论中国古代的五星盈缩差算法[J]. 自然科学史研究, 2011, 30(4): 393～408.

15 魏征, 令狐德棻. 隋书·律历志下[M]. 北京：中华书局, 1973. 492～493.

16 江晓原. 巴比伦天文学与古代中国天文学[J]. 自然辩证法通讯, 1988, 10(1): 26.