辅助线的添加

温静

摘 要：平行线是学生接触比较早的几何图形之一，学生对它的性质判定是比较了解的，但在几何题目的运用解答中往往不容易想到添加平行线来解决问题。利用平行线可以得到角之间的相等或互补的关系，达到转化的目的，为学生带来新的解题思路和方法。

关键词：平行线；同位角；内错角；同旁内角

在新人教版七年级下册教材第五章相交线与平行线中，我们认识了平行线，学习了平行线的判定及性质，在这个过程中我们发现可以由两直线间的特殊位置关系——平行得到三类位置关系角的特殊数量关系：两直线平行，同位角、内错角相等，同旁内角互补。反之，由同位角、内错角相等或同旁内角互补能得出两直线平行。这些结论为我们解决一些求角度或角之间的关系之类问题带来了新的方法和解题思路。

例1：如图，a∥b，M、N分别在a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于____________.

解析：虽然本题中有两平行线，但却不是由两平行线形成的同旁内角。因而想到了过点P构造一条与直线a、b平行的射线，这样又形成的两组平行线就有效地把∠1、∠2、∠3的关系体现出来，从而解决所求角度和的问题。

过点P作PQ∥b，（把图中原先的∠2分成了两个角∠4、∠5）

由题意可得：PQ∥b∥a，∴∠1+∠4=180°，∠5+∠3=180°（三条平行线间的两组同旁内角互补）

根据等式的性质，我们就可以得到∠1+∠4+∠5+∠3=360°

即：∠1+∠2+∠3=360°.

由例1这个基本图形，我们可以继续扩展：如图，a∥b，M、N分别在a、b上，P1，P2，P3，…，Pn为两平行线间的点，顺次连接M、P1、P2、P3、…、Pn、N，形成了（n+2）个角，那么它们的和又有什么规律呢？

由例1我们可以想到分别过P1，P2，P3，…，Pn作直线a的平行线P1Q1，P2Q2，P3Q3，…，PnQn，从而得出a∥P1Q1∥P2Q2∥P3Q3∥…∥PnQn∥b。每相邻的两条平行线间就会形成一组同旁内角，并且它们的和为180°，而所求的（n+2）个角的和就是这些同旁内角的和，由例1的基本图形发现，三条平行线形成两组同旁内角，∠1、∠2、∠3三个角的和是180°的2倍，以此类推，（n+2）条平行线形成了（n+1）组同旁内角，所求的（n+2）个角的和应为180°的（n+1）倍即（n+1）·180°。

例2：已知直線l1∥l2，l3与l1、l2分别交于点A、B，P是直线l3上一点，且不与A、B重合.点E、F分别是l1、l2上一点，且在l3的同侧，连接PE，PF.

（1）若点P在A、B之间移动，请说出∠1、∠2、∠3之间的关系，并说明理由。

（2）若点P在A、B两点的外侧移动，请说出∠1、∠2、∠3之间的关系，并说明理由。

解析：（1）点P是两平行线间的点，有了例1的铺垫不难想到过点P作直线l1的平行线，从而构造出了两组内错角，容易得出∠1、∠2、∠3三个角之间的关系。

过点P作PQ∥l1，（把图中原先的∠3分成了两个角∠4、∠5）

由题意可得：PQ∥l1∥l2，∴∠1=∠4，∠5=∠2（三条平行线间的两组内错角分别相等）∴∠1+∠2=∠3.

（2）若点P在点A的上方移动，我们仍然可以延续第（1）问中的做法.过点P作PQ∥l1，（此时PQ与PE、PF形成了新的角∠4、∠5，并且∠5=∠4+∠3）由题意可得：PQ∥l1∥l2，∴∠1=∠4，∠5=∠2（三条平行线间的两组内错角分别相等）从而把∠5、∠4、∠3转化为了∠1、∠2、∠3的关系即∠3=∠2-∠1.

若点P在点B的下方移动，做法类似，如图，我们容易得出此时∠1、∠2、∠3的关系为：∠3=∠1-∠2.

虽然点P是移动的点，但通过添加平行线，构造出相等的内错角，达到了转化的目的，把分散的三个角转移到了同一点处，使得等量关系一目了然。

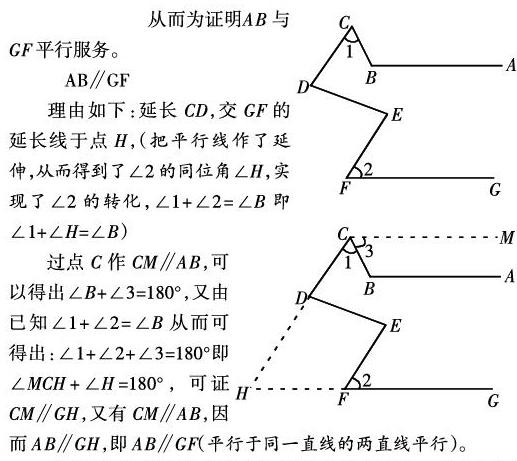
例3：如图所示，已知CD∥EF，∠1+∠2=∠B，试判断AB与GF的位置关系，并说明理由。

解析：很容易判断出AB与GF的位置关系应该是平行，而从现有的图形根据已知条件来说明结论无从入手，因而想到添加辅助线，图形中的拐点较多，容易想到作平行线，通过作平行线把看似毫无关系的∠1、∠2、∠B转化到特殊位置，从而为证明AB与GF平行服务。

AB∥GF

理由如下：延长CD，交GF的延长线于点H，（把平行线作了延伸，从而得到了∠2的同位角∠H，实现了∠2的转化，∠1+∠2=∠B即∠1+∠H=∠B）

过点C作CM∥AB，可以得出∠B+∠3=180°，又由已知∠1+∠2=∠B从而可得出：∠1+∠2+∠3=180°即∠MCH+∠H=180°，可证CM∥GH，又有CM∥AB，因而AB∥GH，即AB∥GF（平行于同一直线的两直线平行）。

本题的综合性较强，添加辅助线的方法也不止一种，而本题中辅助线的添加很好地利用了平行线的性质及判定，达到转化的目的从而证明结论。

通过对平行线的性质及判定的学习，可以发现平行线是一个非常好的几何证明工具，它可以把平行线和角有效地联系起来，可以借助平行得出相等关系的角以及互补关系的角，而通过特殊位置的角的相等关系及互补关系我们又可得出平行的位置关系。平行线只是学习平面几何的开始，相信只要我们用心观察、体会，我们就可以发现很多平行线在证明中的用法，同时也为我们学好平面几何打下良好的基础。

参考文献：

[1]宋桂珂.初中数学辅助线技巧浅略[J].学周刊，2015（6）.

[2]许晶晶.例谈辅助线法在经济生活曲线题中的运用[J].好家长，2015（25）.

编辑 李博宁