城市快速路匝道的最优控制

曾繁荣，干宏程，刘 勇

(上海理工大学 超网络研究中心,上海 200093)

城市快速路匝道的最优控制

曾繁荣，干宏程，刘 勇

(上海理工大学 超网络研究中心,上海 200093)

针对城市快速路控制技术中匝道调节率优化问题，采用宏观动态交通流模型预测实际路网中交通流变化过程，在该模型基础上构建入口匝道最优控制问题，给出基于遗传算法和序列二次规划的混合算法，并对该问题求解。算例结果表明，在最优控制下仿真路段中常发性拥堵问题得到改善，所提出算法能得到较高精度调节率。

智能交通；最优控制；混合算法；城市快速路；宏观动态交通流模型

在城市快速路网研究中，匝道控制作为常用的城市快速路控制技术，一直是研究的热点问题。早在上世纪60年代，计算机技术和交通检测技术匮乏，Wattleworth等根据历史数据，首先使用线性规划的方法求取匝道最优调节率，开始了对入口匝道控制研究及应用[1]。后续Masher等提出一种开环控制策略，控制对象为单匝道，以需求和容量的相互关系为约束，最大限度利用主线的道路资源。早期研究中，提出的数学模型较为理想化，缺乏对于现实情况中入口匝道交通需求和路网上交通需求状况随时间的变化的考虑，并且匝道控制策略本身为开环控制，系统的抗干扰能力差。Papageorgiou和Middelham提出了Alinea算法，将入口匝道处主线下游占有率与期望占有率进行比较确定入口匝道调节率。该算法为闭环控制策略，总体控制方式较为平缓，但仍存在一定的波动[2-4]。Zhang and Ritchie等将神经网络、模糊控制技术用于匝道控制的研究[5]。Hourdakis和Michalopoulos等[6]采用启发式算法对匝道调节率进行优化。国内侯忠生和晏静文等提出了一种带有迭代学习前馈的快速路无模型自适应入口匝道控制算法[7]。庞明宝等提出了基于遗传算法高速公路混沌系统模糊延迟反馈匝道控制[8]。李健等提出循环等待时间等作为目标参数，应用向量机设计协调控制方法，以深化匝道协调控制研究[9]。柴干和谢永利结合非支配性快速遗传算法对多个性能指标进行综合优化的高速公路匝道控制方法[10]。对以往研究的考察，匝道控制研究在优化技术、控制理论、模糊控制和神经网络等方面都取得了一些成果。本研究兼顾实时工况与算法运行效率，采用遗传算法和序列二次规划相结合的混合算法有效且高效地解决匝道调节率优化问题,力求仿真条件更加符合实际控制特点，使得最优控制方法的评价更加科学准确。

1 入口匝道最优控制问题的构造

城市快速路控制策略有匝道控制、主线控制、路径诱导等，还有一系列的管制措施，其中匝道控制最为常见。入口匝道控制表现为优先满足主干道的交通需求，限制入口匝道上的车辆流入主干道，即入口匝道处汇入主干道流量与主干道的通行能力有关，也与主干道当前交通状态和匝道处排队车辆数目有关，常发性拥堵路段控制效果较为显著。

1.1 宏观动态交通模型

城市快速路自身就是一个极其复杂的系统，具有不确定性、多样性和非线性等特点。半个世纪以来，从宏观层面对城市快速路的研究取得了丰富的成果。欧洲学者Papageorgiou等建立的宏观动态交通流模型(Metanet)能够确切地展现城市快速路动态非线性特征，解释现实交通状态中冲击波、产生拥堵及消散和停停走走的现象[11-12]。

在对城市快速路进行仿真中，宏观动态交通流模型作为过程模型，其由路段模型、节点模型和排队模型3部分组成[13]。

路段模型用于描述城市快速路上交通状态在离散化的时间和空间上的变化。由下述表达式构成

qm,i(k)=ρm,i(k)vm,i(k)λm

(1)

(2)

(3)

(4)

式中，qm,i(k)、ρm,i(k)和vm,i(k)分别表示在路段m第i小段k时刻的流量、密度和平均速度；κ、υ、τ为常量参数；V[·]为稳态速度-密度关系；vf,m、ρcr,m分别为m路段上的自由流速度和临界密度。

节点模型用于描述在道路几何属性发生变化(车道合流或者分流)处、出(入)口匝道和立交等位置，交通状态量承前启后的过程。由下述表达式构成

(5)

(6)

(7)

(8)

排队模型用来计算和描述在主干道流量、主干道和匝道通行能力等条件限制下，流入主干道和匝道处形成排队的车辆。由下述表达式构成

w0(k+1)=w0(k)+T[d0(k)-q0(k)]

(9)

(10)

(11)

(12)

q0,2(k)=Q0min{1,(ρmax-ρμ,1(k))/(ρmax-ρμ,cr(k))}

(13)

式中，w0(k)为kT时刻起点O处排队长度；d0(k)为(kT,(k+1)T)时间段内起点O处的交通需求量；Qo为起点处单车道最大流入能力；ρmax和ρμ,dr分别为路段μ的堵塞密度和临界密度。当O处为入口匝道时，ro为匝道调节率(ro∈[0，1])。

1.2 最优控制问题的构造

在入口匝道处，通过匝道调节率控制周期内车流汇入主线，在时间维度上进行交通流的控制，从而调整入口匝道处上游、下游的交通状态量，即流量、速度和密度。极小化目标函数一般形式为

(14)

式中，k为仿真时标；X(k)为所有交通状态量，即流量、速度、密度和排队等等组成，中间过程由交通流模型决定，即X(k+1)=f(X(k),U(kc),D(k))；D(k)为系统运行中外部扰动，如交通需求量；kc为控制时标，由控制周期决定，在同一控制周期中U(kc)保持不变。

交通评价指标有总行程时间(TTT)、总排队时间(TWT)和总花费时间(TTS)等。总行程时间用于计算在考察路网所有车辆在仿真时间内从进入城市快速路到离开城市快速路所花费的时间，单位为veh·h。总排队时间用于计算在考察路网中路网起点和匝道入口处车辆的等待时间，单位为veh·h。总花费时间是总行程时间和总排队时间之和，用于从全局的角度对路网性能进行考察，单位为veh·h，数学表达式分别为

(15)

(16)

(17)

以往研究中，一般采用路网中总花费时间(TTS)作为最优控制问题中的目标函数[14-16]，目标函数为

(18)

2 城市快速路网匝道最优控制方案

2.1 控制变量设定

在匝道调节率优化求解过程中，将仿真时间离散化处理，离散化为k个仿真步长，即仿真时间为t=kT，每个仿真步长T的取值一般为4～10 s。在实际的交通管制过程中，入口匝道处信号灯的工作周期C一般为40～100 s，为仿真步长T的整数倍，即C=nT。

在考察实际交通管制措施合理性的同时，需兼顾算法的求解效率。在常发性拥堵路段往往交通需求量已经接近路段的通行能力，且在需要管控的时间里交通需求量的波动不大。将仿真时长等量地划分为z段控制周期，z的数目由该算法适当求解规模而定。每个控制周期的时长相当于m个入口匝道信号灯工作周期的时长。综上所述，决策向量可表示为U={u0,u1,…ui,…,uz}，决策向量与实际交通管制过程中信号灯周期中控制量的对应关系为

ui=u(im+1)=u(im+2)=…=u(im+m)

(19)

决策变量取值满足ui∈[0,1]。实际信号灯控制中只有红和绿两种情况，信号灯为红灯的时候取值为0，绿灯的时候取值为1。在一个信号灯工作周期内，信号灯状态为绿灯状态的时长为CG=(u(ic)×n)T。

2.2 求解算法

本文将城市快速路网匝道的最优控制转换为非线性规划问题。在求解该问题时，给出基于遗传算法和序列二次规划算法的混合算法。遗传算法不依赖于初始解的选取，且寻优速度较快。序列二次规划算法虽然优化能力较强，但是对初始值较敏感。本文将首先利用遗传算法给出城市快速路网匝道的最优控制的满意解，再将求得的解作为初始值，利用序列二次规划进一步优化搜索，充分发挥两种解法的优势，提高算法的求解精度。本文给出的混合算法主要步骤如下：

步骤1 初始化处理。设置交通流模型参数，以及遗传算法参数(种群规模，基因数目，交叉概率，变异概率，最大遗传代数等)，决策变量取值范围，随机生成初代种群；

步骤2计算目标函数值和适应度评估，目标函数根据宏观动态交通流模型建立的，即交通流模型的计算。取目标函数值的倒数为适应度函数进行每个个体的适应度评估；

步骤3 进行遗传算法的核心操作，即选择、交叉、变异；

步骤4 若达到遗传算法最大迭代次数，则转入步骤5。若没达到遗传算法最大迭代次数，则转入步骤2；

步骤5将当前的最好匝道调节率作为初始值，利用序列二次规划算法进行求解；

步骤6输出算法得到的最优匝道调节率。

3 路网算例

3.1 路网描述及仿真条件

以两个起点两个终点的快速路网为例，对常发性拥堵路段做仿真，考察匝道调节对路网运行效率的影响。快速路网的拓扑结构图如图1所示，路网中包含2个起点(O1、O2)和2个终点(J1、J2)，节点和路段编号标于图中。其中，O1为主线上游流入口，O2为入口匝道，J1为出口匝道，J2为主线下游流出口。路段L1、L2、L3都为4车道，L1和L3长度均为5 km，L2长度为4 km,每小段为1 km。

图1 仿真情景设置

假设，正值主干道机动车车流量高峰期几乎没有车流从出口匝道 流出，但有一定车流量从入口匝道 汇入该主干道。交通需求量如图1(b)所示，模拟早晚高峰交通量急骤上升，并给该路段造成相当大的负担，因而产生常发性拥堵。交通流模型参数取值参照以往研究中标定的数据。自由流车速取110 km/h，临界密度取33.5辆/(km·车道)，主干道上游处 的单车道通行能力为2 000辆/h，入口匝道处 的单车道通行能力为1 500辆/h。以上述数据建立起路网仿真案例，分别在不控制和控制两种情形下进行仿真，对常发性拥堵路段在出行高峰期(仿真时长近160 min)进行模拟，并考察匝道调节对路网运行效率的改善情况。

3.2 不控制情形下路网运行情况

在不采取任何控制措施的情况下，分别得到仿真路网交通流密度和速度的时间-空间状态图，演示路网中交通状态量的变化。图2是反映各个路段交通流密度的变化，图形中x轴表示仿真时长，y轴表示路段编号(短线后是该路段小段编号)。在图2中交通流密度越大，图中对应的色彩灰度越浓。更直观地表现为，图中灰度较深的部位所对应在该时间段内该路段交通处于拥堵状态，且灰度越深，拥堵的程度也越严重。

由仿真结果可得，伴随着交通需求高峰期的到来，交通需求量的急剧增加，由入口匝道汇入主干道的车流量增加，率先造成入口匝道下游处拥堵，从而造成主干道上的拥堵，并持续延长主线上拥堵发生的时间，并随着时间推移向入口匝道上游和下游都有不同程度的扩散。

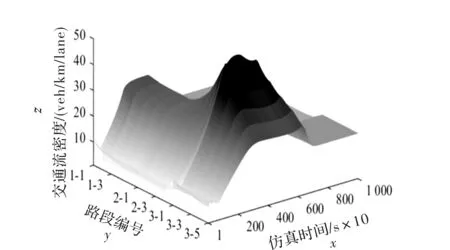
图2 不控制情形下路网:交通流密度时空状态图

3.3 最优控制情形下路网运行情况

在匝道最优控制系统的运作下，得到能达到系统最优的匝道调节率，将该匝道调节率转换成信号灯工作周期内的绿信比。通过匝道入口信号灯绿灯和红灯这两种状态不断地更替，来限制从匝道驶入主干道车流量。

在匝道最优控制下，得到的仿真结果如图3所示，图形中的各个属性、各个标号以及颜色变化与相应数值均与上述不控制情形下路网运行时空状态图中一致。

图3 最优控制情形下路网:密度时空状态图

通过与不控制情形下各个路段的交通流密度、平均速度的对比，发现主干道上交通情况得到很好的改善，代表拥堵情形的灰色区域大幅度减少。从空间上看，拥堵产生和扩散的路段数目大量减少，使得绝大部分的车能够在临界交通流密度下行驶；从时间上看，车辆陷入拥堵状况的时间和拥堵状况延长的时间也显著减少。

3.4 控制基本效果测试

在匝道最优控制下，通过仿真结果中展现的全局时空状态变化图可以看出仿真路网各个路段交通状态都得到的不同程度的改善。但在匝道入口下游处还是处于色彩灰度最浓的状态。利用仿真过程中存储的数据，可以对仿真路网中某一部分进行分析。以匝道入口下游处(路段3第1小段，即L3,1)和匝道入口O2为例，来测试匝道最优控制的控制效果。

图4 仿真结果测试

图4(a)～图4(c)分别表示的是最优控制轨迹图即匝道入口O2交通信号灯绿信比、匝道入口下游处路段的密度ρ3,1和速度v3,1这3种交通状态量，在不控制和匝道最优控制情形下实时变化。由图4(b)所示，在匝道最优控制下，仿真路网交通状态不稳定的L3,1处面临交通需求高峰期的考验，依然能使得交通流密度值约维持在40，并且在仿真过程中始终低于或等于不控制情形下交通流密度。在图4(c)中，在匝道最优控制下，L3,1处面临交通需求高峰期的考验，能使得交通流速度值约维持在60，并且在仿真过程中始终高于或等于不控制情形下交通流速度。速度维持在60 km/h保证城市快速路正常的运作，也能保证满意的出行质量。

表1 最优控制调节下测试结果

综合整个路网系统的行程时间和排队时间，虽增加了匝道排队，但换来了整体效率的显著提高。交通效益评价数据由表1可得，优化匝道调节率后的TTS是3 191.945辆·h，比不控制情形下减少了2.31%。最优控制下行程时间相较于不控制下，减少了5.03%。虽然增加了排队时间，但显著缓解拥挤，改善了路网整体的运行效率，提高了车辆行驶速度，增加服务流量等。

4 结束语

针对城市快速路上常发性拥堵情况，结合现实匝道信号灯周期性工作情况，进行了仿真研究。研究聚焦于城市快速路控制技术中匝道调节率的优化问题，基于现有的宏观动态交通流模型预测路况变化和构造系统中入口匝道的最优控制问题，采用混合算法求解。实验结果显示，本文方法得到的匝道调节率，能有效地改善城市快速路上的拥堵情况，提高路网的整体运行效率。

[1] Wattelworth J, Berry D. Peak period control of a freeway system-some theoretical investigations[J].Highway Research Record, 1965,89(2):16-25.

[2] Papageorgiou M, Blosseville J M, Hadj-salem H.Modelling and real-time control of traffic flow on the southern part of boulevard peripherique in paris: part i: modelling [J].Transportation Research Part A: General,1990,24(5):345-359.

[3] Papageorgiou M, Hadj-salem H, Blosseville J M. Alinea: A local feedback control law for on-ramp metering [C].Alex: Transportation Research Record,1991.

[4] Papageorgiou M, Hadj-salem H, Middelham F. Alinea local ramp metering: Summary of field results[J].Transportation Research Record: Journal of the Transportation Research Board,1997,16(3): 90-98.

[5] Zhang H, Ritchie S, Recker W. Some general results on the optimal ramp control problem[J].Transportation Research Part C: Emerging Technologies,1996,4(2):51-69.

[6] Hourdakis J, Michalopoulos P. Evaluation of ramp control effectiveness in two twin cities freeways[J].Transportation Research Record: Journal of the Transportation Research Board,2002,18(11):21-29.

[7] 侯忠生,晏静文.带有迭代学习前馈的快速路无模型自适应入口匝道控制[J].自动化学报, 2009,35(5): 588-595.

[8] 庞明宝,贺国光,马宁.基于遗传算法高速公路混沌系统模糊延迟反馈匝道控制[J]. 土木工程学报,2009,42(3):125-131.

[9] 李健,贾元华,陈峰.高速公路转向快速路的匝道控制[J].深圳大学学报:理工版,2011,28(5):466-470.

[10] 柴干,谢永利.高速公路匝道多性能指标优化控制方法[J].中国公路学报,2012,25(6): 115-122.

[11] Papamichail I, Kotsialos A, Margonis I, et al.Coordinated ramp metering for freeway networks-A model-predictive hierarchical control approach[J].Transportation Research Part C:Emerging Technologies,2010,18(3): 311-331.

[12] 干宏程.面向控制的城市快速路网宏观动态交通模型[J].系统工程,2007,25(11):1-5.

[13] Iordanidou G R, Roncoli C, Papamichail I,et al.Feedback-based main-stream traffic flow control for multiple bottlenecks on motorways[J].IEEE Transactions on Intelligent Transportation Systems,2014(3):1-12.

[14] Keyvan-Ekbatani M，Papageorgiou M，Knoop V L.Controller design for gating traffic control in presence of time-delay in urban road networks[J].Transportation Research Part C: Emerging Technologies，2015，59(1):308-322.

[15] Kan Y, Wang Y, Papageorgiou M,et al. Local ramp metering with distant downstream bottlenecks: A comparative study[J].Transportation Research Part C: Emerging Technologies，2016,62(2):149-170.

[16] 干宏程.VMS诱导信息影响下的路径选择行为分析[J].系统工程,2008(3):11-16.

The Optimal Control of the Ramp in Urban Freeway

ZENG Fanrong，GAN Hongcheng，LIU Yong

(Center for Supernetworks Research, University of Shanghai for Science and Technology, Shanghai 200093, China)

When it comes to the problem of how to control the ramp in freeway efficiency. We adopt macroscopic dynamic traffic flow model to predict the change process of traffic flow in actual road network. And then we established a ramp optimal control problem on the basis of the first step. Finally to solve this problem more effective we employed the hybrid optimization algorithm of GA and SQP.as the result shows not only the congestion problem has been improved greatly in the simulation road but also the algorithm works efficiently. Thus high accuracy adjustment rate could direct got by this algorithm adopted.

intelligent transportation; optimal control; hybrid optimization algorithm; expressway; macroscopic dynamic traffic flow model

2016- 05- 18

国家自然科学基金资助项目(51008195)；上海市自然科学基金资助项目(15ZR1428100)；上海市一流学科基金资助项目(S1201YLXK)

曾繁荣(1993-)，男，硕士研究生。研究方向：智能交通。干宏程(1978-)，男，教授，博士生导师。研究方向：交通规划等。

10.16180/j.cnki.issn1007-7820.2017.02.013

TP273+.5；U491

A

1007-7820(2017)02-049-05