体会“统计与概率”中的四大思路

体会“统计与概率”中的四大思路

陈廷亮

概率论是统计学的基石，统计学来源于旧时的赌博.当时的赌徒们通过历史数据的记录，逐渐总结出了描述性统计.利用这些描述性统计的数据，他们的胜率直线上升.哪个稳赚哪个会赔，哪个波动大没规律，这些经验逐渐成了一种智慧，体现在之后的各个领域里.

我们平时都将概率论和统计学合称为“概率统计”，但显然这两者是有关系，却又不是统一的.统计和概率是方法论上的区别，一个是推理，一个是归纳；一个是对原理的讨论，一个是对方法的讨论.

学习“统计与概率”要注意以下几个要点：1.在学习过程中要抓住对概念的引入和背景的理解，这实际上是一个抽象过程；2.在学习过程中对于引入概念的内涵和相互间的联系及差异要仔细推敲；3.在解题过程中不要为解题而解题，而应理解题目所涉及的概念及解题的目的，因此概率学习的关键不在于做多少习题，而在于要把精力放在理解不同题型涉及的概念及解题的思路上去.这样往往能“事半功倍”，同时学起来就不会枯燥而且容易记忆.下面就统计与概率相关题型和解答技巧与同学们交流分享.

第一类：用分类讨论思想解决掷骰子、摸球、转盘类应用问题

例1 现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、 4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是（ ）.

【分析】每个骰子都有6种可能，投掷这两枚骰子，所有可能结果共有36种，其中点数之和为9的有（3，6），（4，5），（5，4），（6，3）4种，所以，所求概率为：

【点评】把统计与概率问题与我们常规的数学思想相联系，这样方便归纳解题方法.

例2 一个布袋内只装有1个红球和2个黄球，这些球除颜色外其余都相同，随机摸出一个球后放回搅匀，再随机摸出一个球，则两次摸出的球都是黄球的概率是_______.

【分析】用列表法将所有可能的结果列举出来，再利用概率公式求解即可.

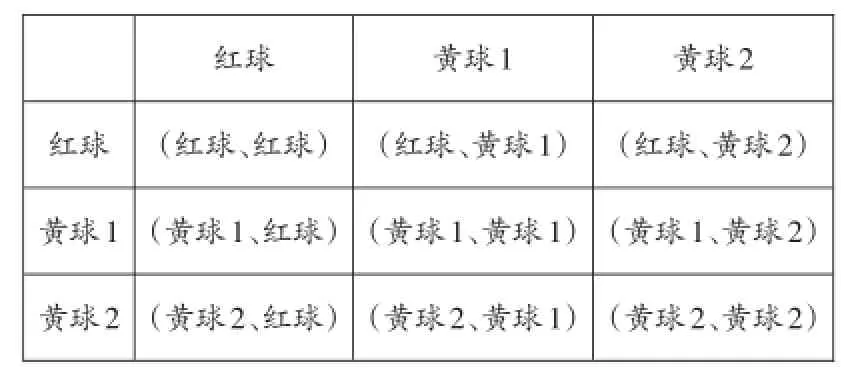
红球黄球1黄球2红球（红球、红球）（黄球1、红球）（黄球2、红球）黄球1（红球、黄球1）（黄球1、黄球1）（黄球2、黄球1）黄球2（红球、黄球2）（黄球1、黄球2）（黄球2、黄球2）

【点评】列出每种颜色球出现的全部可能，再计算都是黄球的概率.

例3 如图是一个能自由转动的正六边形转盘，这个转盘被三条分割线分成形状相同、面积相等的三部分，且分别标有“1”“2”“3”三个数字，指针的位置固定不动.让转盘自动转动两次，则指针指向的数都是奇数的概率为.

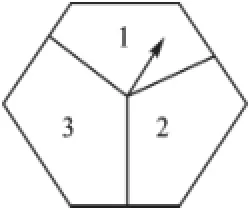
【点评】把每次出现相同数字的情况全部列出，再计算都是奇数的概率.

例4 如图，转盘A的三个扇形面积相等，分别标有数字1，2，3，转盘B的四个扇形面积相等，分别标有数字1，2，3，4.转动A、B转盘各一次，当转盘停止转动时，将指针所落扇形中的两个数字相乘.（当指针落在扇形的交线上时，重新转动转盘.）

（1）用树状图或列表法列出所有可能出现的结果；

（2）求两个数字的积为奇数的概率.

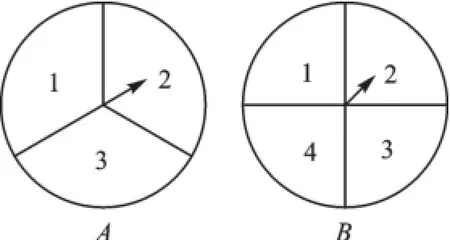
【分析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；

（2）先算出两个数字的积为奇数的情况，再利用概率公式即可求得答案.

解：（1）画树状图得：

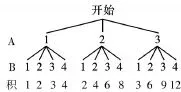
则共有12种等可能的结果；

（2）两个数字的积为奇数的情况有4种，则两个数字的积为奇数的概率为：

【点评】此题考查了列表法或树状图法求概率.

第二类：用大数规律解决硬币抛掷类问题

例5 在课外实践活动中，甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率，其实验次数分别为10次、50次、100次、200次，其中实验相对科学的是（ ）.

A.甲组 B.乙组 C.丙组 D.丁组

【点评】大量反复实验时，某事件发生的频率会稳定在某个常数的附近，这个常数就叫做事件概率的估计值.本题考查了模拟实验.选择和抛硬币类似的条件的实验验证抛硬币实验的概率，是一种常用的模拟实验的方法.

第三类：用比例解决估算类问题

例6 为了估计鱼塘中的鱼数，养鱼者首先从鱼塘中捕获30条鱼，在每条鱼身上做上记号后，把这些鱼放归鱼塘，再从鱼塘中打捞200条鱼，如果在这200条鱼中有5条鱼是有记号的，则鱼塘中鱼的数量估计为_________.

【点评】设未知数，用成比例关系进行估算解决此类问题.

第四类：对统计数据的处理问题

例7 下列说法正确的是（ ）.

A.了解飞行员视力的达标率应使用抽样调查

B.一组数据3，6，6，7，9的中位数是6

C.从2000名学生中选200名学生进行抽样调查，样本容量为2000

D.一组数据1，2，3，4，5的方差是10

【点评】全面调查和抽样调查是按调查对象范围不同划分的调查方式.中位数是指将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数.样本容量又称“样本数”，是指一个样本的必要抽样单位数目.方差是各个数据分别与其算术平均数之差的平方的和的平均数.

例8 某中学篮球队12名队员的年龄如下表：

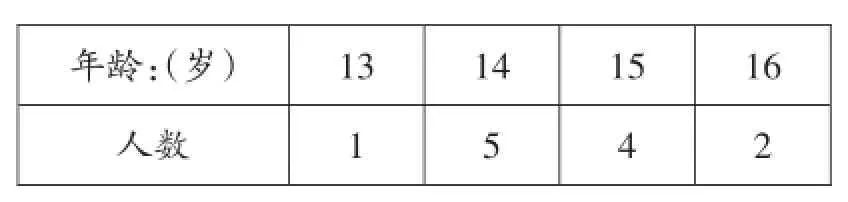
年龄：（岁）人数1 3 1 1 4 5 1 5 4 1 6 2

关于这12名队员的年龄，下列说法错误的是（ ）.

A.众数是14 B.极差是3

C.中位数是14.5 D.平均数是14.8

【点评】众数、中位数、极差、平均数是统计的基础知识点.找对数据就可以轻松解题.

例9 为了了解某学校学生每周平均课外阅读时间的情况，随机抽查了该学校m名同学，对其每周平均课外阅读时间进行统计，绘制了如下条形统计图（图1）和扇形统计图（图2）.

条形统计图

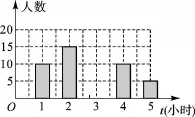
图1

扇形统计图

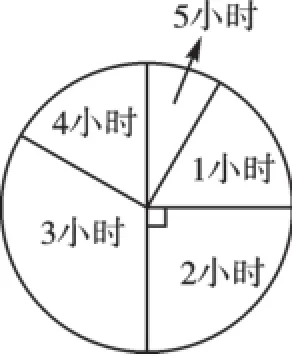
图2

（1）根据以上信息回答下列问题：

①求m的值；

②求扇形统计图中阅读时间为5小时的扇形圆心角的度数；

③补全条形统计图.

（2）直接写出这组数据的众数、中位数，求出这组数据的平均数.

【点评】本题考查了众数、中位数、平均数及扇形统计图和条形统计图的知识，解题的关键是能够结合两个统计图找到进一步解题的有关信息，难度不大.

上面的四类方法供同学们在平时的训练中运用和体会，也期待同学们有更好的方法与我们共同分享.

（作者单位：江苏省建湖县建阳中学）