例谈中考数学压轴题最值问题的思维分析与解题策略

林年生

（上杭县教师进修学校,福建上杭364200）

例谈中考数学压轴题最值问题的思维分析与解题策略

林年生

（上杭县教师进修学校,福建上杭364200）

文章以2016年福建省龙岩市中考数学求最值问题为例，从解题思维过程和解题策略两个方面进行了详细分析，从学生的最近发展区入手，通过有用捕捉、有关提取、有效组合三个方面展示了其思维过程，并用有效的解题策略来指导，让一个抽象的思维过程，变成了一个简单明了的思维过程。

最值问题；思维分析；解题策略

最值问题是初中数学的一大难点，也是中考命题中各知识的结合点和能力考查的区分点，素有“综合性强、难度大和区分度高”等典型特点。如何才能找到突破此类问题的方略?笔者结合2016年龙岩市中考试题第25题，就中考压轴题中最值问题的解题思维过程与解题策略，谈谈自己的看法，以期同行斧正。

一、试题呈现

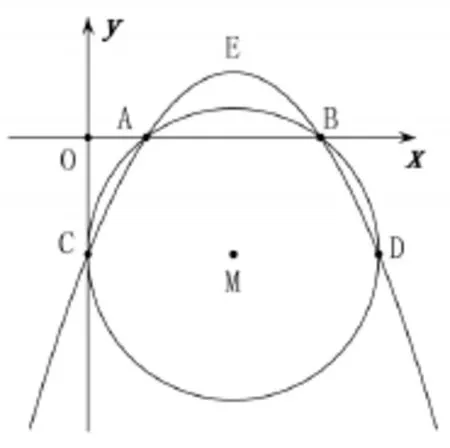
图1

（1）求a值及A，B两点坐标；

（2）点P(m,n)是该抛物线上的动点，当∠CPD为锐角时，请求出m的取值范围；

（3）点E是抛物线的顶点，⊙M沿CD所在直线平移，点C，D的对应点分别为点C′，D′，顺次连接A，C′，D′，E四点，四边形AC′D′E（只要考虑凸四边形）的周长是否存在最小值？若存在，请求出此时圆心的坐标；若不存在，请说明理由。

二、思维过程分析

解题的过程就是信息的获取、存储、处理和输出，在这个的过程，从精心审题，捕捉基本信息，到温故知新，提取有关信息，最后去伪存真，组合有效信息进行解题，充分反映了解题者的心路历程，分析这个过程中的知识结构和逻辑关系，是提高解题能力的有效途径。

1.有用捕捉

有用捕捉是指从审题中捕捉有用的信息，包括从题目的文字叙述中捕捉符合信息和从题目的图形中获取形象信息。

（2）从题目的图形中获取形象信息，抛物线与y轴的交点是C，OC=2；点A、B、C、D既是抛物线上的点，又是圆上的点；第（2）小题中P(m,n)是抛物线上的点，且∠CPD为锐角；第（3）小题中四边形AC′D′E的边AE，C′D′是定值，存在点C′，D′使四边形AC′D′E的周长最小。

2.有关提取

有关提取是指从自己的记忆储存中提取有关信息，包括概念、公式、定理、法则、基本题型、解题模型、解题方法等，这些信息是解题继续推进的依据。

概念：点和圆的位置关系，凸四边形，周长最小值。

方法：待定系数法；一元二次方程的解法；图形的轴对称、平移。

公式：抛物线y=a(χ-h)2+k的对称轴是χ=h，顶点是(h,k)。

法则：二次函数与一元二次方程的关系，函数图象与坐标的关系，一元一次不等式解集。

定理：勾股定理及其逆定理；90°的圆周角所对的弦是直径；两边成比例且夹角相等的两个三角形相似。

题型1：解二元一次方程组（人教版《义务教育教科书·数学》七年级下册第八章第二节“消元——解二元一次议程组”第91～92页例1）。

题型2：求一次函数解析式（人教版《义务教育教科书·数学》八年级下册第十九章第二节“一次函数”第93页例4）。

模式1：A，B两点在直线l的同侧，直线上存在唯一一点P，使PA+PB的值最小。

模式2：村庄A，B位于小河的两侧，若河岸彼此平行，则可建一座与河岸垂直的桥CD，使A村到B村的路程最近。

3.有效组合

有效组合是指将从题目中捕捉到的有用信息与从记忆储存中提取的有关信息结合起来思考，并画出解题的思维过程，使之成为一个和谐的逻辑结构。如图2，是第（2）小题的思维结构图。

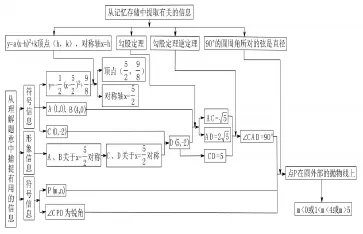
图2

三、解题策略

数学解题策略是指解数学题过程中所采取的总体思路，是带有原则性的思想方法，它既能指导思维模式的灵活运用，又能统率各种具体的解题方法与较小的模式。研究解题策略是一个从实践上升到理论，又用理论去指导实践的过程，对提升解题能力有良好的帮助。

1.模式识别

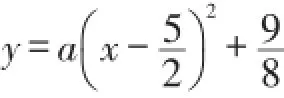
2.动静转换

动和静是事物状态表现的两个侧面，它们相比较而存在，依情况而转化，动中有静，静中寓动。在数学解题中，可用动的观点来处理静的数量和形态，表现为以动求静。也可反过来，用静的方法来处理动的事物，表现为以静制动，因为事物在运动中总会有一些稳定的状态，抓住这些不变的性质或不变量，可以作为解题的突破口。如第（2）小题求m的取值范围，因m是点P的横坐标，所以实际是问点P在运动过程中是否在某个时候满足∠CPD<90°。注意到点A、B、C、D的特殊性，容易猜想∠CAD=90°,∠CBD=90°，因此只要能说明CD是⊙M的直径，问题便迎刃而解了。

由（1）知，

如图3，连接AD，AC，CD，则CD=5，∵A(1，0),C(0，-2),D(5，-2)，∴AC=5，AD=25，∴AC2+AD2=CD2，∴CD为⊙M的直径，∴当点P在圆外部的抛物线上运动时,∠CPD为锐角，∴m的取值范围是m<0或15。

图3

第（3）小题求四边形AC′D′E周长的最小值，由于⊙M沿CD所在直线平移，实际就是线段CD在平移，因只要考虑凸四边形的情形，也就是只能在直线AE的右边移动，取其某个时刻的位置C′D′，就是要求四边形AC′D′E周长的最小值。

3.数形结合

大家知道，数形结合是指在研究问题的过程中，注意把数和形结合起来考虑，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，进而达到化难为易的目的。数形结合是研究数学问题的有效途径和重要策略，它体现了数学的和谐美、统一美。第（3）小题求四边形AC′D′E周长的最小值，这个问题看上去是四条线段和的最值，注意到线段EA、C′D′是定值，其实就是两条线段AC′、D′E之和的最值问题．由图可看到线段AC′、D′E虽然在定直线CD的同侧，但与模式1区别在于这两条线段没有公共端点，故要把这两条线段中的某一条移到新的位置，使其与另一条线段对接即可，联想到模式2中运用的平移变换手法，可将线段AC′平移至D′F（或将线段D′E平移至C′F）。则AF=C′D′=CD=5,又∵A(1,0)，∴F(6,0)，作点E关于直线CD的对称点E′，连接EE′正好过点M，交χ轴于点N，∵抛物线顶点，直线CD为，连接E′F交直线CD于点H，则当点D′与点H重合时，四边形AC′D′E的周长最小。

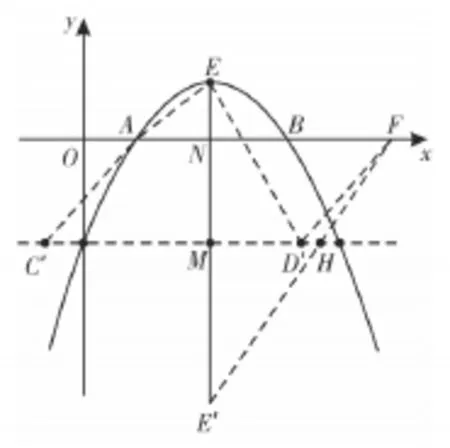
图4

4.差异分析

以第（3）小题为例来找目标差。最显著的目标差是：

⊙M沿CD所在直线平移，点C，D的对应点分别为点C′，D′，顺次连接A，C′，D′，E四点，四边形AC′D′E（只要考虑凸四边形）的周长是否存在最小值。

因四边形AC′D′E的边AE、C′D′是定值，若使四边形AC′D′E周长最小，只要使AC′+D′E的和最小，目标差减少，根据模式1，这样的点通过作图是存在的（如图4），目标差进一步减小，进而转化为求点D′（或C′）的坐标，求点D′的坐标可以通过求直线E′F的解析式来解决，也可以用相似三角形的性质来解决。

［1］义务教育教科书·数学（七—九年级）［M］.北京：人民教育出版社，2013．

［2］罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008．

［3］李永明.捕捉、提取、组合、反馈四阶段解题的思维剖析与思考［J］.中学数学，2015（7）．

（责任编辑：王钦敏）