3-RRR并联机器人运动学建模与仿真

张乾坤 高 洪

（安徽工程大学，安徽 芜湖 241000）

并联机器人是机械与计算机控制技术的产物[1]，Hunt教授在1978年首次提出把六自由度并联机构作为机器人操作器[2]，从而在世界范围内掀起了对并联机器人研究的热潮。并联机器人的国内研究始于1991年，1991年燕山大学黄真教授[3]研制出我国第一台6自由度并联机器人样机，并且在1997年出版了我国第一部关于并联机器人理论与技术的专著。进入21世纪，随着科研工作者对并联机器人认知的不断加深，少自由度并联机器人由于其独特的结构逐渐受到人们的青睐。少自由度并联机器人不仅具有并联机器人无累积误差，精度较高特点还能有效改善并联机器人相对于串联机器人工作空间小的缺点，因此，针对不同机型，对相关问题的研究仍有必要[4-7]。3-RRR并联机器人是一种典型的平面少自由度并联机器人，在精密加工、电子制造装备等领域具有良好的应用前景[8]，以3-RRR并联机器人为基础，还可以构建具有打磨、拾放功能的新型机器人[9]。为此，本文针对3-RRR并联机器人，建立其逆解模型，通过MATLAB编程进行运动学仿真，以探求动平台位姿的变化与主动杆角位移、角速度以及角加速度变化之间的关系。

1 运动学分析

1.1 机构描述

如图1所示，3-RRR并联机器人是由动平台C1C2C3，机架三角形A1A2A3，主动杆A1B1、A2B2、和A3B3，从动杆B1C1、B2C2和B3C3组成。其中动平台和机架三角形均为正三角形，主动杆杆长AiBi=l1（i=1，2，3，下同。）从动杆杆长BiCi=l2，O为机架三角形A1A2A3的外接圆中心，其半径为OAi=R。P为动平台C1C2C3外接圆中心，其半径PCi=r。O-XY为固定坐标系，X轴平行于A1A3。αi为主动杆AiBi与固定坐标系X轴正方向的夹角（逆时针为正），βi为从动杆BiCi与固定坐标系X轴正方向的夹角（逆时针为正），θ为C1C3与固定坐标系X轴正方向的夹角（逆时针为正），动平台与机架三角形之间用串联支链链接，其中每个串联支链均包含一个主动杆和一个从动杆。主动杆与机架、主动杆与从动杆、从动杆与动平台之间皆用转动副连接。

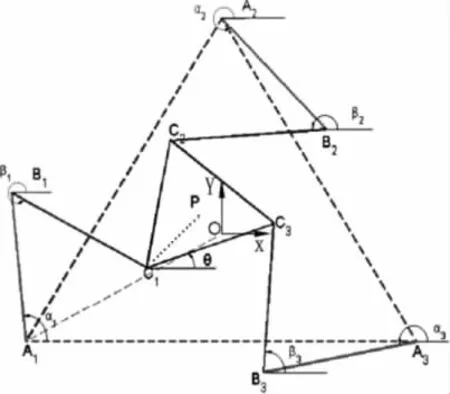
图1 3-RRR并联机器人示意图

1.2 运动学逆解

3-RRR并联机器人动平台C1C2C3在平面XY内运动，其系统结构参数具有对称性，根据闭环几何约束条件我们可以得到：

（1）式分别向X轴Y轴投影，可以得到两个约束方程：

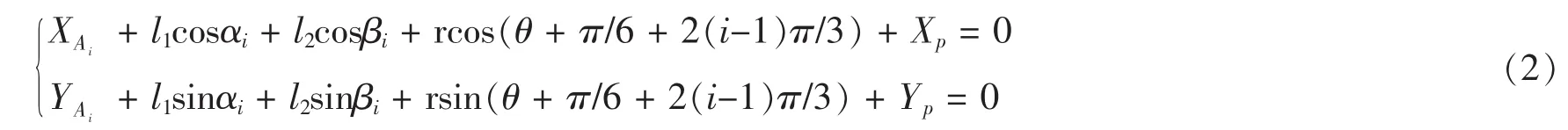
其中：

令 X＝tan（αi/2），将式（3）化简得：

其中：

对一元二次方程（5）进行求解，得：

对于3-RRR并联机器人的其中一条支链，当Bi2－4AiCi>0时，αi有两个解，对应其分子的“±”，每个主动杆转角按式（7）计算得到工程中两种不同的装配模式，3-RRR并联机器人共有三条支链，按照排列组合规律，共有8种装配模式，依次记为+++模式、++-模式、+--模式、+-+模式、---模式、-+-模式、-++模式、-+-模式。

求式（3）关于时间t的一阶导数，得主动杆的角速度：

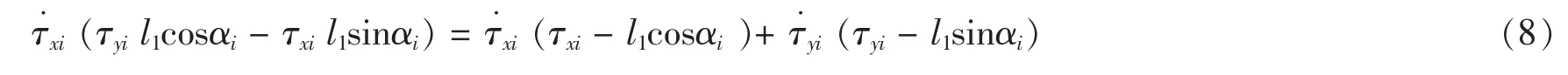
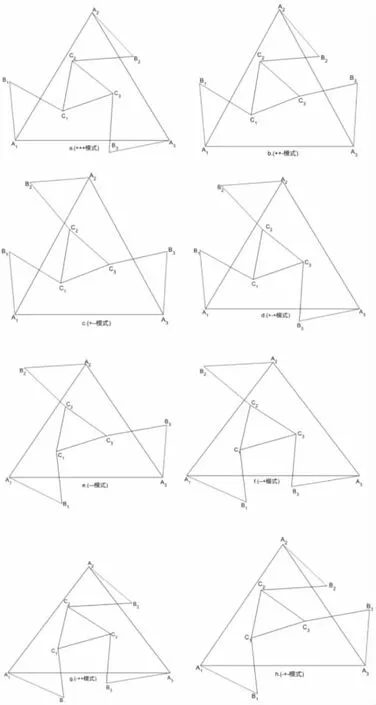
图2 3-RRR并联机器人8种装配模式图

写成矩阵形式为:

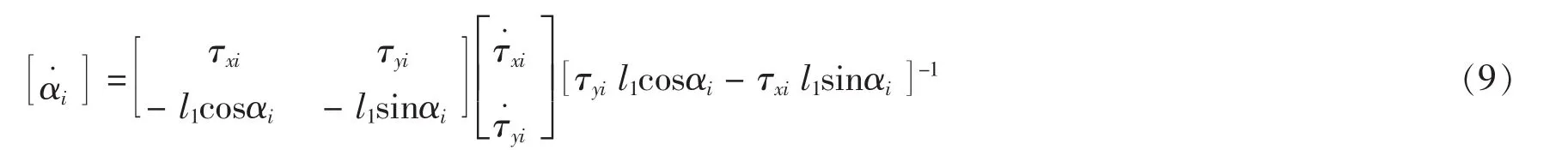
其中：

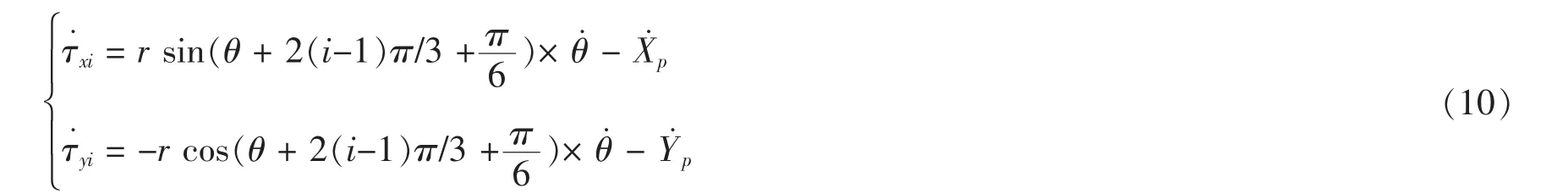
再求式（8）关于时间t的一阶导数，得主动杆的角加速度：

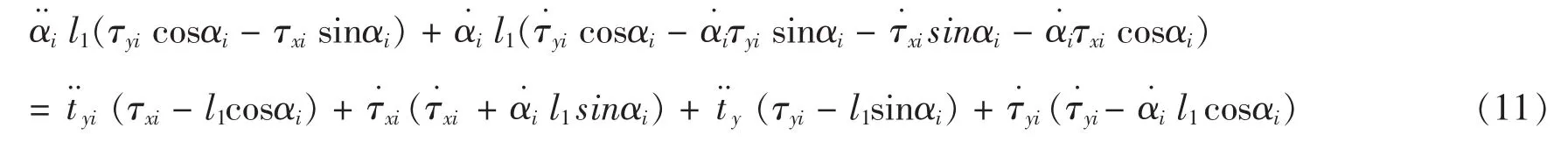
其中：

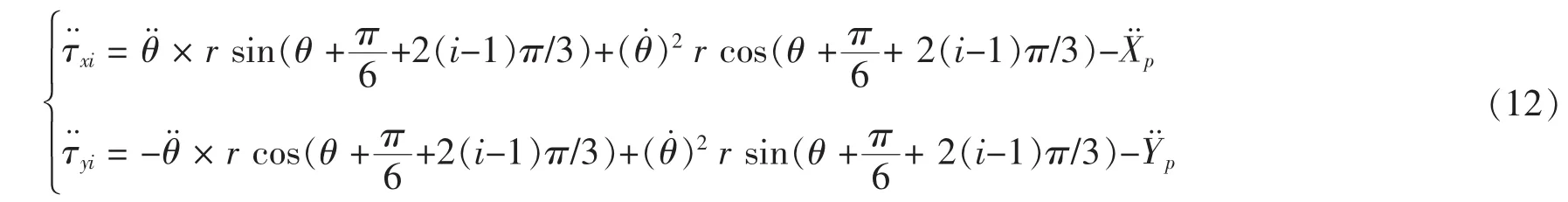
2 运动仿真

使用MATLAB对3-RRR并联机器人逆运动学进行仿真，观察主动杆的运动轨迹。3-RRR并联机器人共有8种装配模式，如图2所示。

根据机构学原理，一旦该机构装配完成，只能以一种装配模式工作，为此，不失一般性，选择第一种（+++)模式进行仿真分析，其余装配模式同理分析即可，不赘述。假设 。动平台的运动轨迹为：

其中，长度单位为mm；即动平台在XY平面内以点（0，-30）为圆心，以30 mm为半径做圆周运动，在仿真时间t=2πs内，动平台转角θ范围为[0，π/9]。

仿真结果如图3、图4、图5所示：

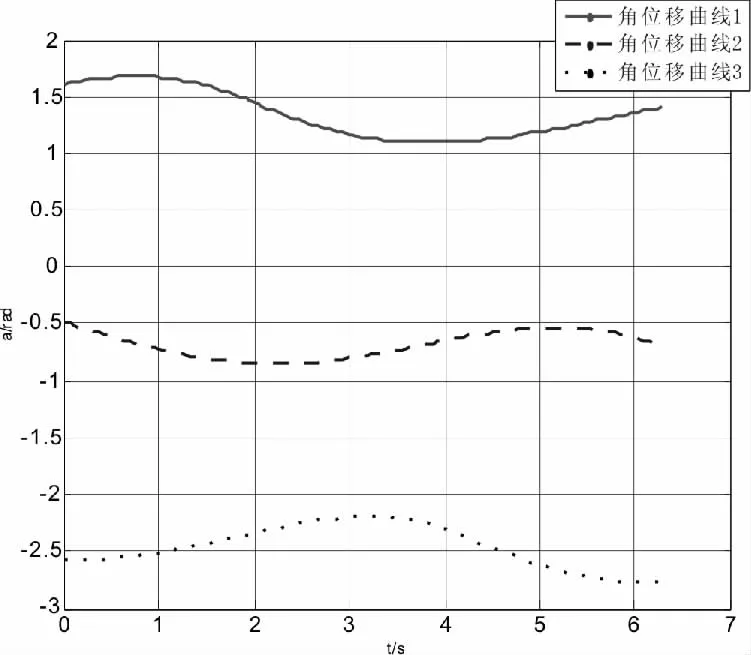
图3 主动杆角位移图

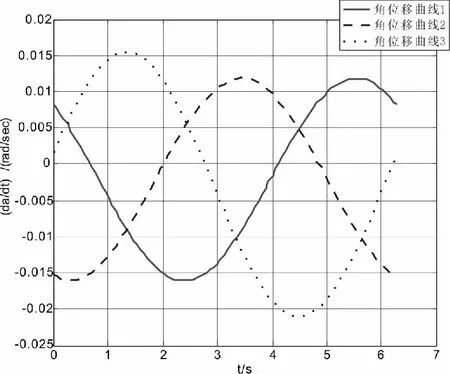
图4 主动杆角速度图

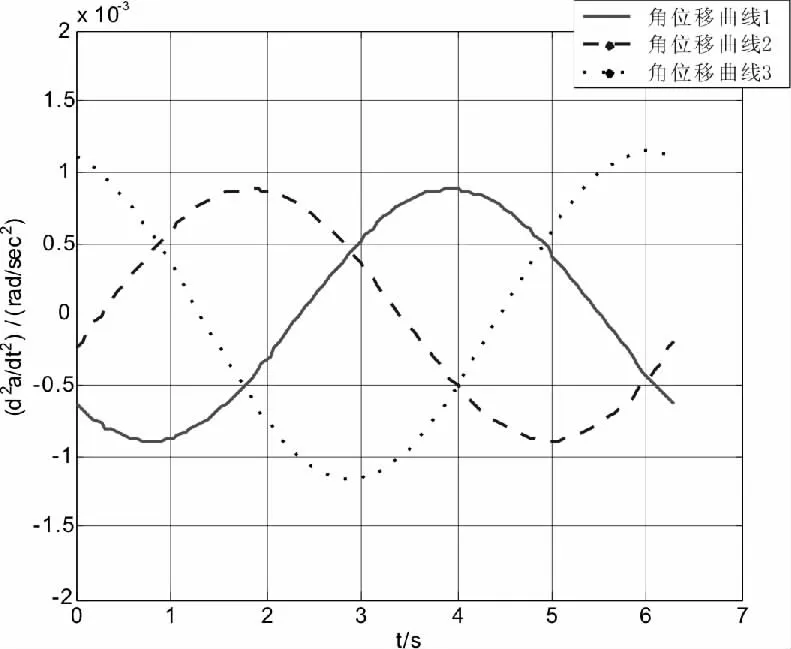
图5 主动杆角加速度图

在（+++）装配模式下，当动平台外接圆中心做圆周运动，且其姿态角θ[0，π/9]时，三个主动杆角位移具有二级连续性，正因为其角加速度连续，所以该机构具有良好的动力学特性。

3 结论

基于3-RRR并联机器人逆解，可得到主动件运动规律，通过MATLAB编程和仿真，可得到不同装配模式下，主动杆角位移、角速度和角加速度的变化规律，从而判断其动力学特性优劣。

[1]高洪，赵韩.并联机器人机构学理论研究综述[J].安徽工程大学学报，2006，（1）：73-79.

[2]HUNT K H.Kinematic geometry of mechanism[M].CLARENDON，1978.

[3]黄真，孔令富，方跃法.并联机器人机构学理论及控制[M].北京;机械工业出版社，1997.

[4]曹丽亚，崔建昆.3-RRR平面并联机器人工作空间边界求解和灵活性研究[J].机械传动，2016，（8）：38-42.

[5]WU J，WANG J，YOU Z.A comparison study on the dynamics of planar 3DOF 4-RRR，3-RRR and 2-RRR parallel manipulators[J].Robotics and Computer-Integrated Manufacturing，2011，（1）：150-156.

[6]HAMDOUN O，BAKKALI L E，BAGHLI F Z.Analysis and optimum kinematic design of a parallel robot☆[J].Procedia Engineering，2017，（181）：214-220.

[7]高名旺，张宪民，刘晗.3-RRR高速并联机器人运动学设计与实验[J].机器人，2013，（6）：716-722.

[8]SHAO Z，TANG X，XU C.Inertia match of a 3-RRR reconfigurable planar parallel manipulator[J].Chinese Journal of Mechanical Engineering，2009，（6）：791-799.

[9]高洪，张伟，肖平，等.具有大工作空间的四自由度混联机器人：201510671336.5[P].2017-05-31.