复杂输入下变步长算法的改进及其应用*
王 新, 王丹璐
(1.河南理工大学 物理与电子信息学院,河南 焦作 454003;2.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
复杂输入下变步长算法的改进及其应用*
王 新1, 王丹璐2
(1.河南理工大学 物理与电子信息学院,河南 焦作 454003;2.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
针对变步长算法的选取对自适应滤波器的性能有重大影响,而复杂输入下谐波对自适应滤波器的误差信号及步长有较大影响的问题,在常用变步长算法的基础上,提出了一种改进变步长算法。该算法根据调节过程调整原算法的系数,实现在调整初期具有较大的步长,而在调整后期具有足够小的步长,以获得较好的滤波效果。仿真分析和实例分析均表明:采用基于改进变步长算法的自适应滤波器进行变频调速下转子断条故障诊断,具有较高的可靠性。
自适应滤波器; 变步长算法; 转子断条; 变频调速
0 引 言
转子断条是鼠笼式异步电动机常见故障之一。由于鼠笼式异步电动机的转子无直接电气元件引出,所以,直接对转子进行故障检测比较困难。随着故障诊断技术的发展,采用非侵入式故障诊断方法可以准确地诊断转子断条故障。该方法主要是通过对电机运行参数进行分析与处理,来实现对断条故障的准确诊断。从检测与分析参数的角度来看,主要有定子电流、失电电压、转矩、振动、温度等信号,其中基于定子电流分析的转子断条故障诊断方法最为常见[1~3]。
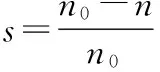
然而,在变频调速下,受变频器影响电动机定子电流的谐波成分复杂,不仅有变频器输出频率及其整数次谐波,而且还有间谐波及噪声干扰[8~11]。由于自适应滤波器的滤波效果很大程度上取决于变步长算法,而目前常用的变步长算法主要是根据自适应滤波器的误差信号进行调整,调整过程中步长随着误差信号的减小而按照一定规律减小[12,13]。这样,变频调速下的复杂谐波成分使得自适应滤波器趋于稳定时误差信号增大,导致步长较大,自适应滤波器的陷波带宽较大,从而影响自适应滤波器的滤波效果。所以,变频调速下的复杂谐波成分给基于自适应滤波器的转子断条故障诊断方法造成了十分不利的影响。
为此,本文针对变频调速下的复杂谐波成分对自适应滤波器的影响,根据自适应滤波器调节过程中误差信号ε(k)的变化规律,提出了一种的改进变步长算法。它不仅具有较快的收敛速度,而且当权系数接近最佳权系数时,具有较小的步长,获取较窄的陷波带宽,从而克服复杂谐波成分的影响,取得良好的滤波效果。最后,将改进变步长算法应用于变频调速下转子断条故障诊断,通过实例分析,验证了改进变步长算法的良好效果。
1 自适应滤波器的工作原理
自适应滤波器的工作原理如图1所示。图中,d(t)为原始输入信号,x(t)为参考输入信号,其中x(t)=C·cos(2πf0t),式中C为参考信号的幅值, f0为待陷波的频率。d(k),x1(k),x2(k)分别为d(t),x1(t),x2(t)在kT时刻(T为采样周期)的采样值,w1(k),w(k)为权值采样值,ε(k)=d(k)-y(k),其中y(k)为滤波器输出。
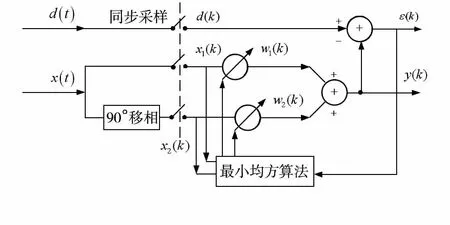
图1 自适应滤波器的原理图
由图1可知,误差信号为
ε(k)=d(k)-y(k)
(1)
权的修正过程为
w1(k+1)=w1(k)+2με(k)x1(k)
(2)
w2(k+1)=w2(k)+2με(k)x2(k)
(3)
为了兼顾自适应滤波器的收敛速度和滤波效果,自适应滤波器通常采用变步长取代固定步长。这样,当权系数远离于最佳权系数,使用较大的步长,加速收敛速度;当权系数接近于最佳权系数时,使用较小的步长,获取较小的均方误差[14~18]。此时,权的修正过程为
w1(k+1)=w1(k)+2μ(k)ε(k)x1(k)
(4)
w2(k+1)=w2(k)+2μ(k)ε(k)x2(k)
(5)
2 变频调速下复杂谐波成分对自适应滤波器的影响
2.1 自适应滤波器的陷波带宽
对于上述自适应滤波器,可以求得其闭环传递函数为
(6)
式中 ω0=2πf0。由于通常μC2很小,所以闭环系统的极点为
z=(1-μC2)cosω0±j[(1-2μC2)- (1-μC2)2cos2ω0]1/2
(7)
|z|=(1-2μC2)1/2
(8)
极点在单位圆内,系统是稳定的。
上述自适应滤波器的陷波带宽BW为
BW=2μC2rad
(9)
可见,自适应滤波器的陷波带宽BW与步长μ成正比。因此,步长μ越小,越有利于克服频率为f0信号的影响[14~18]。
2.2 常见的变步长算法
对于自适应滤波器而言,变步长算法的选取十分关键,它对自适应滤波器的滤波效果有重大的影响,其中式(10)所示的变步长算法[13](以下称之为原算法)应用非常广泛
(10)
式中 α,β0,m均为待定的正数。实验表明,对于基于自适应滤波器的转子断条故障诊断,在电动机采用工频电源直接供电情况下,该变步长算法具有很好的应用效果。
2.3 变频调速下的自适应调节过程
由于在自适应滤波器中参考输入信号x(k)是幅值固定的余弦信号,误差ε(k)在自适应调节过程中是衰减振荡的,而当自适应调节过程趋于稳定时,ε(k)近似为幅值固定的交变信号。变频调速下自适应滤波器的实际输入信号d(k)是变频器输出信号,它包含基波频率成分及其它复杂频率成分。此时x(k)的频率取d(k)的基波频率。当自适应调节过程趋于稳定时,ε(k)基本不包含d(k)的基波成分,但是ε(k)中仍会包含d(k)的其它复杂频率成分。这样,就导致自适应滤波器趋于稳定时ε(k)较大。由于式(10)中步长μ(k)与 ε(k)有关,所以,在自适应调节过程中,μ(k)受ε(k)增大的影响,尽管μ(k)是衰减的,但是稳定时μ(k)仍较大。由式(9)可知,此时自适应滤波器的陷波带宽BW较宽,当转子断条故障特征频率接近基波频率时,自适应滤波后该故障特征频率可能被滤去,导致无法获得。所以,变频调速下复杂谐波成分对自适应滤波器的步长有很大的影响,从而影响了自适应滤波器的滤波效果。
3 变步长算法的改进与比较
3.1 改进的变步长算法
针对变频调速下复杂谐波成分对自适应滤波器步长的影响,为了使变步长算法在自适应调节过程中快速收敛,且趋于稳定时陷波带宽较窄。本文针对式(10)所示的原算法,提出了一种改进的变步长算法(以下称之为改进算法),即
(11)
式中 β(k)可以采用
(12)
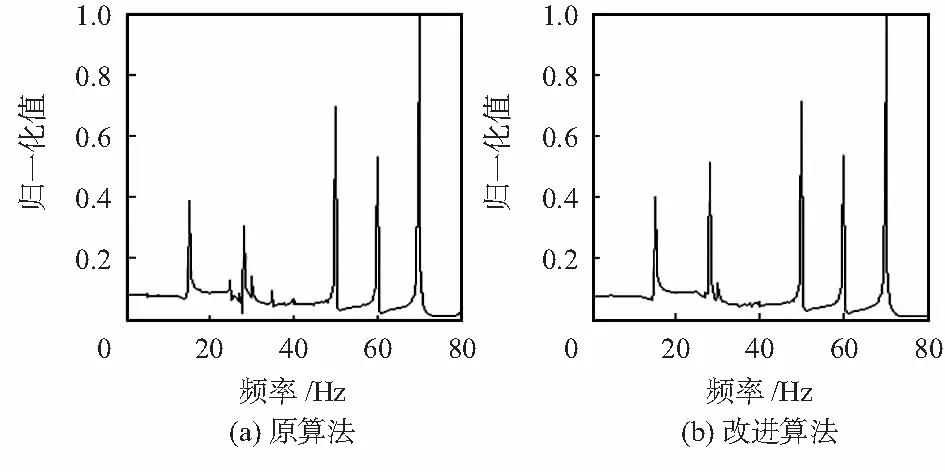
式中 c1,c2为待定系数,其中0 改进算法的基本思想如下:在自适应调节过程的初期,采用原算法,步长较大,滤波器快速收敛;随着自适应滤波器趋于稳定,由于此时误差ε(k)波动的峰值减小很慢,μ(k)的峰值减小也很慢,所以,通过逐步改变β(k),使步长μ(k)明显减小,以获得较窄的陷波带宽。 实验证明,当取α=50,β0=0.3,m=1时,原算法可以取得较好的效果;在原算法参数取值基础上,当取c1=c2=0.2,M1=100,M2=500时,改进算法可以取得很好的效果。下面的仿真分析与实例分析,均在上述参数基础上进行分析与比较。 3.2 仿真信号构造方法 为了便于比较不同算法的滤波效果,在忽略了远离基波及含量较低的其它谐波频率成分情况下,根据变频调速下转子断条故障信号的特点,构造信号如下 (13) 式中 f0为基波分量(也即变频器的输出频率);f1为断条故障特征频率分量,A1为该分量的幅值,通常情况下A1=0~0.05;f2~f5分别为模拟变频调速下的复杂谐波频率分量,A2~A5分别为其幅值。 3.3 故障诊断判别方法 由于一般情况下f1与f0非常接近,快速傅里叶变换(FFT)分析时,频率分辨率取值应该比较高。在本文分析中,采样频率fs=1 000Hz,待分析信号采样点数N=4 096,所以频率分辨率为 Δf=fs/N=0.244Hz (14) 在实际故障诊断系统中,通过测量定子电流和电动机转速,可以方便地计算出基波频率f0和断条故障特征频率f1。当然,是否存在f1分量还需要进一步做自适应滤波处理与分析,这也是本文的核心。 在以下的FFT分析中,幅值谱密度值均采用归一化处理,即幅值谱密度值最大值Vmax为1。显然,在自适应滤波之前,Vmax在f0处,而在自适应滤波之后,Vmax对应频率则需要根据实际信号的谐波分布来确定,通常情况下Vmax不会在f0处。 考虑到转速测量可能存在一定误差,影响f1频率值的计算,所以故障诊断判别方法如下:如果在(f1-2Δf,f1±2Δf)范围内,幅值谱密度值存在极大值V1,且V1≥ε0(在本文系统中取ε0=0.1),那么存在转子断条故障;否则,不存在转子断条故障。 3.4 仿真分析与比较 参考输出频率为30Hz的实际测量信号的主要谐波分布情况,取f0=30Hz,f1=28Hz,A1=0.02;f2=15Hz,A2=0.021,f3=50Hz,A3=0.028;f4=60Hz,A4=0.022;f5=70Hz,A5=0.041;同时,为了分析方便,取C=1。 假定Va,Vb分别为采用自适应滤波器处理前、后的f1分量的幅值谱密度值。对于信号d(k),由于自适应滤波之前原算法与改进算法所用信号相同,所以,两者的Va值相同,经分析,Va=0.015 5。采用原算法与改进算法进行自适应滤波之后,得到的信号的FFT分析结果如图2(a),(b)所示,Vb的具体数值如表1所示。 表1 两种算法的效果 图2 仿真信号滤波后FFT分析结果 由Va,Vb可知,自适应滤波之后故障特征明显了许多。同时,由表1可知,改进算法的Vb值是原算法的1.68倍,所以,采用改进算法对f0分量的滤波效果比采用原算法的滤波效果要好许多。 实验系统中,变频器型号为VFD037M43A,鼠笼式异步电动机的型号为TYPE100—4,电动机额定转速n1=1 430 r·min-1,极对数p=2,电源频率为50 Hz,采样频率fs=1 000 Hz,采样点个数为N=4 096,f0为变频器输出频率,f1为实际定子电流信号的断条特征频率。自适应滤波前的变频器不同输出频率下的Va值如表2所示。以变频器输出频率f0=30 Hz为例,其FFT分析结果如图3所示,图中最大分量频率为f0,为了便于观察其它谐波分量,图中幅值取0.2。 表2 不同输出频率下滤波前的实验结果 图3 实际信号滤波前的FFT分析结果 由图3可以看出,变频调速下实际定子电流信号谐波较多,同时f1与f0非常接近,这对f1分量的提取有很大影响。由于FFT分析时f0分量对f1分量影响很大,表2中的Va值比实际值小许多,所以,利用自适应滤波前的FFT分析结果进行转子断条故障诊断,结果是不可靠的。 由于自适应滤波器滤去了f0分量的主要成分,所以,自适应滤波后幅值谱密度值最大的频率分量一般不再是f0分量,而是自适应滤波前幅值谱密度值仅次于f0分量的某一谐波分量。由于该谐波分量频率距离f0较远,自适应滤波后该谐波分量基本不受影响,所以,Vb可以更好地反映两种算法的优劣。不同输出频率下采用上述两种算法自适应滤波后的Vb值如表3所示,其中r表示滤波后改进算法与原算法的Vb值之比。为了直观比较,以变频器输出频率为30 Hz为例,给出采用两种算法进行自适应滤波后的FFT分析结果,分别如图4(a)和(b)所示。 从表3可以看出,在不同输出频率下改进算法的Vb值均比原算法大,改进算法具有较好的处理效果,这将有利于断条故障特征的提取。实验证明,自适应滤波后在(f1-2Δf,f1±2Δf)范围内的极大值V1为Vb,所以可以根据Vb进行故障诊断,诊断结果完全正确。但是,由于部分频率下原算法的Vb值与ε0=0.1相比裕量很小,所以利用原算法进行故障诊断的可靠性比改进算法低许多。 表3 不同输出频率下滤波后的实验结果 图4 仿真信号滤波后FFT分析结果 实验证明:变频调速下复杂谐波成分对自适应滤波器的步长有很大影响,从而影响了自适应滤波器的滤波效果。改进变步长算法充分考虑了自适应滤波器调节过程中复杂谐波对误差信号ε(k)及步长μ(k)的影响,通过根据调节过程调整原算法的系数,实现变步长算法在调整初期具有较大的步长,而在调整后期具有足够小的步长,可以获得较好的滤波效果。仿真和实例分析均表明,采用基于改进变步长算法的自适应滤波器进行变频调速下转子断条故障故障诊断,比原算法具有更高的可靠性。 [1] 田慕琴,王秀秀,宋建成,等.笼型异步电动机转子断条故障诊断方法[J].电机与控制学报,2015,19(6):14-21. [2] 祝洪宇,胡静涛,高 雷,等.负载连续变化时鼠笼电机早期转子断条故障诊断[J].仪器仪表学报,2014,35(7):1646-1653. [3] 许伯强,孙丽玲,孙俊忠.异步电动机定子故障检测新算法[J].电力自动化设备,2008,28(10):14-18. [4] 马宏忠,姚华阳,黎华敏.基于Hilbert模量频谱分析的异步电机转子断条故障研究[J].电机与控制学报,2009,13(3):371-376. [5] 安永红,夏昌浩.笼型异步电动机转子断条故障诊断技术[J].电力学报,2006,21(3):310-311. [6] 王榕生,吴汉光,黄灿水,等.多断条笼型转子感应电动机导条电流分布[J].电机与控制学报,2010,14(4):59-65. [7] 许伯强,李和明,孙丽玲,等.小波分析应用于笼型异步电动机转子断条在线检测初探[J].中国电机工程学报,2001,21(11):24-28. [8] 安国庆,刘教民,郭立炜,等.相关性消去法诊断变频电源笼型电机转子断条故障[J].电机与控制学报,2012,16(3):47-52. [9] 阳同光,蒋新华,付 强.瞬时功率频谱分析在牵引电机转子故障诊断的应用研究[J].电机与控制学报,2012,16(10):96-99. [10] 李功新,黄彦婕,江修波.基于自适应陷波滤波器的谐波分析法[J].电力自动化设备,2013,33(9):100-104. [11] 罗 铭,刘振兴,黄 菲.变频电源笼型异步电机断条故障诊断仿真[J].电机与控制学报,2008,12(2):139-142. [12] 包 明,王云亮.改进的变步长自适应谐波检测算法[J].电力自动化设备,2011,31(1):71-74. [13] 罗小东,贾振红,王 强.一种新的变步长LMS自适应滤波算法[J].电子学报,2006,34(6):1123-1126. [14] 贺洪江,王春霞.一种新的LMS自适应滤波算法分析仿真研究[J].传感器与微系统,2012,3l(3):15-17,21. [15] 刘国海,吕汉闻,刘 颖,等.基于改进RLS算法的谐波电流检测方法[J].电力自动化设备,2010,30(10):46-49. [16] 张俊敏.基于改进型自适应算法的谐波检测及其性能研究[J].电力自动化设备,2011,31(4):23-26. [17] 吴 斌,赵学增,滕志军.基于自适应陷波器的工频电力通信信号检测[J].电力系统自动化,2003,27(20):35-39. [18] 高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(8): 1094-1097. Improvement of variable step size algorithm under complex input and its application* WANG Xin1, WANG Dan-lu2 (1.School of Physics and Electronic Information Engineering,Henan Polytechnic University,Jiaozuo 454003,China;2.College of Information Science and Engineering,Northeastern University,Shenyang 110819,China) The variable step size algorithm affects the performance of the adaptive filter heavily,and the harmonic in complex input severely affects error and step size of the adaptive filter.To solve these problems,an improved variable step size algorithm is put forward based on common variable step size algorithm.In order to obtain a good filtering effect,the improved algorithm gets a bigger step size in the initial adjustment and a small enough step size in the later adjustment by adjusting the coefficient of the original algorithm.The simulated analysis and the example analysis show that the fault diagnosis of the broken rotor bar in the variable frequency speed regulation has high reliability by using the adaptive filter based on the improved variable step size algorithm. adaptive filter; variable step size algorithm; broken rotor bar; variable frequency speed regulation 10.13873/J.1000—9787(2017)03—0153—04 2016—03—11 国家自然科学基金资助项目(61403129); 河南省科技攻关项目(142102210048) TN 911.7 A 1000—9787(2017)03—0153—04 王 新(1967-),男,博士,教授,博士生导师,主要从事故障诊断、电气传动和信号处理方向研究工作。
4 变频调速下断条故障特征提取




5 结 论

