基于RSSI的自适应权重定位算法*

刘宏立， 周 登， 徐 琨， 胡久松

(湖南大学 电气与信息工程学院,湖南 长沙 410082)

基于RSSI的自适应权重定位算法*

刘宏立， 周 登， 徐 琨， 胡久松

(湖南大学 电气与信息工程学院,湖南 长沙 410082)

在室内环境中，由于存在多径、反射的影响，采用传统的静态权重质心定位(SWCL)方法无法得到准确的定位精度。针对这一问题，提出了一种新的基于接收信号强度指示(RSSI)的动态自适应静态权重质心定位(RSSI—DA—SWCL)算法。对RSSI测距算法优化，消除不同发射功率和其它突发干扰对测距的影响；利用锚节点和未知节点距离等信息，让锚节点自适应地获得最优的权重系数，从而提高定位精度；将RSSI—DA—SWCL算法在ZigBee平台中实现，并通过Maltab仿真和实测实验对算法进行验证。结果表明：和传统的定位算法相比，提出算法具有更优的定位精度。

无线传感器网络； 动态加权； 质心定位算法； 接收信号强度指示测距

0 引 言

无线传感器网络[1，2](wireless sensor networks，WSNs)是一种将大量低成本、低功耗的传感器节点随机布置到特定的区域,节点实现自控组织的多跳网络。

WSNs定位算法分为两大类：基于测距定位和非测距定位[3]。基于测距主要有质心定位算法、DV-Hop算法等。非测距定位主要有接收信号强度指示(received signal strength indication,RSSI)、到达时间(time of arrival,ToA) 和灯塔测量法。静态权重定位算法[4～6]结合测距和非测距定位算法的优点，提高了定位精度，然而该算法采用的是静态权重系数，这样无法充分利用锚节点的信息，甚至导致占主导作用的锚节点由于静态权重系数的影响反而增大了定位误差。针对这个问题，本文在井下巷道真实环境下做了大量的实验，并统计分析大量的RSSI数据，在此基础之上提出了一种基于RSSI动态自适应静态权重质心定位 (RSSI dynamic adaptive static weighted centroid location，RSSI—DA—SWCL) 算法，即让各个锚节点自适应获得最优权重修正系数，这样可以提高占有主导作用的锚节点的影响力，从而提高定位的精度。

1 静态权重定位算法

1.1 静态权重算法原理

静态权重定位算法是质心定位算法的改进，引入了权重系数，权重系数体现了距离远近对定位精度的影响。图1为静态权重定位算法原理图，其中，B1,B2和B3为锚节点，P为待定位的节点。

根据静态权重定位算法的原理，其未知节坐标计算

图1 静态权重定位算法原理图

(1)

式中 wj为权重系数，一般表示距离之间的函数[7]

(2)

式中 δ作为一个固定的权重修正系数，它体现了各个锚节点对质心坐标决定权的大小。

1.2 权重修正系数特性分析

δ作为一个固定的系数，它是否取得最优解直接决定算法的优劣。在研读资料文献后发现最优的权重修正系数一般在区间(1,4)之间取得。

1)定位区域大小的改变

在定位区域内部署10个锚节点和2个未知节点，增加均值为0，方差为1的高斯白噪声，在区间(1,4)内权重修正系数以0.1为步长逐渐递增，利用式(1)计算未知节点定位误差仿真结果如图2和表1所示。

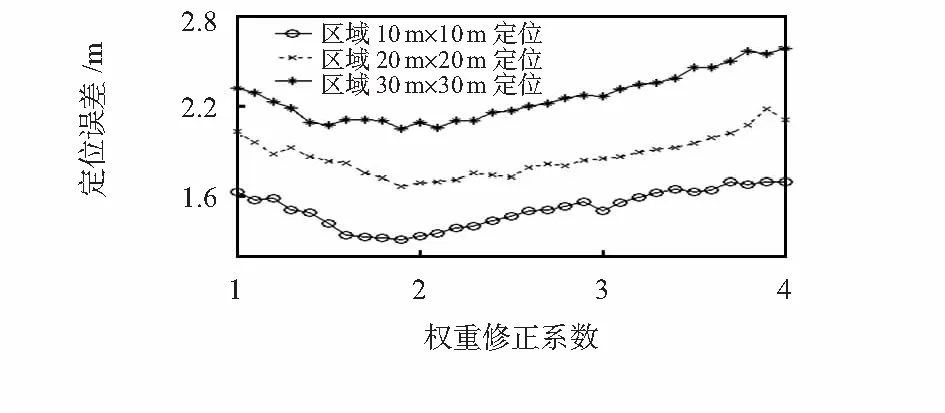
图2 定位区域对权重修正系数影响图

定位区域/m2误差范围/m最优修正系数10m×10m1.31～1.711.920m×20m1.67～2.121.930m×30m2.05～2.591.9

2)不同高斯噪声影响

在定位区域中分别加入均值为0，方差为1,2,3,4,5的高斯噪声，其他参数同上述相同，按照上述步骤进行仿真，仿真结果如图3和表2所示。

图3 高斯噪声对权重修正系数影响图

表2 高斯噪声对权重修正系数影响

3)不同锚节点的影响

在定位区域中锚节点从10,15,20,25,30开始递增，其他参数同上述相同，按照上述步骤进行仿真，其结果如图4和表3所示。

图4 锚节点对权重修正系数影响图

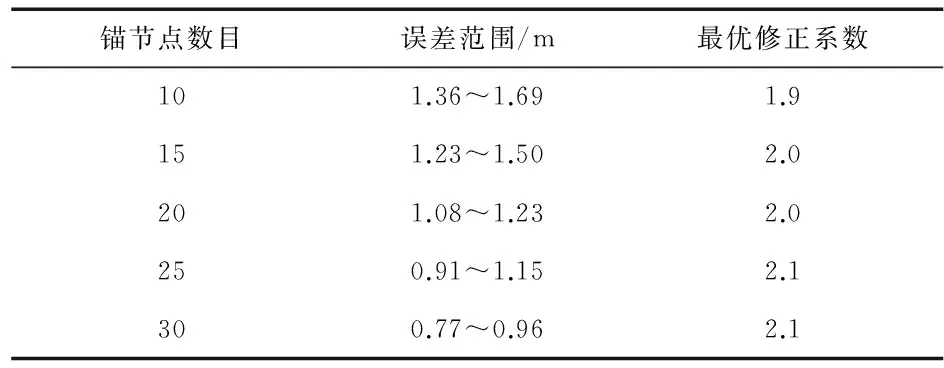
表3 锚节点对权重修正系数影响

从上述分析可以知道，定位区域、高斯噪声对权重修正系数影响不大，其对应的最优的权重修正系数均是1.9。而当锚节点数目发生改变时，对应的最优的权重修正系数也发生改变。因此下文主要分析在不同的锚节点数目区域中如何取得最优的权重修正系数。

2 RSSI-DA-SWCL定位算法

2.1 RSSI测距算法优化

传统RSSI测距[8]原理图1所示，采用正态—对数模型[9]，其在d处接收的RSSI为

RSSI=A-10nlgd

(3)

式中A为1 m处接收信号强度，n为衰减因子。RSSI测距优化主要分为以下3个阶段：

阶段1 在真实室内环境中，每个未知节点接收大量的RSSI数据，将这些RSSI数据求初始平均值

(4)

式中 n为测量次数，实验结果表明：当n适当增大时，定位精度也就越高。

阶段2RSSI经过多次测量后，通过高斯分布函数滤除突发干扰造成的偏差比较大的值，去除小概率事件。然后求二次平均值，这样RSSI值精度会更高

(5)

通过设定高概率最小值应大于0.6的范围，则可知

0.15σ+u≤x≤3.09σ+u

(6)

阶段3 由于发射节点的发射功率不一致，本文针对这个问题消除式(3)中参数A和n，从而消除不同功率带来的影响。由图1所示，锚节点B1接收其他锚节点和未知节点的信息分别为

RSSIB2B1=AB1-10nB1lg(dB2B1)

(7)

RSSIB3B1=AB1-10nB1lg(dB3B1)

(8)

RSSIB3P=AB1-10nB1lg(dB3P)

(9)

对式(7)、式(8)、式(9)进行求差和作商，则

随着物联网的快速发展，超低功耗设计已经成为了模拟集成电路领域研究者的重点研究方向[1]。在可预见的未来，超低功耗模拟集成电路的发展将给可穿戴智能设备、智能家居、无线传感器网络等低功耗应用带来革命性的变化[2]。基准电流源和基准电压源是模拟/混合信号集成电路的重要组成部分，它们为电路设计提供了与稳定的参考电流和参考电压。在超低功耗模拟/混合信号集成电路设计中，要求其拥有极低的功耗以及较高的电源电压和温度特性，以满足超低功耗的要求。

(10)

(11)

如式(11)所示，消除参数A和n的影响，从而消除了不同发射功率的影响，提高了RSSI测距的精度。

2.2RSSI-DA-SWCL算法分析

定位区域中不同数目的锚节点对应最优权重系数是不一样的，因此，有必要研究权重修正系数在什么情况下增加或者减少。将式(1)中锚节点拆分成单个锚节点对未知节点的影响，并在定位区域从n个锚节点中随机选取第t个锚节点，分析不同的修正系数对该节点的影响

(12)

(13)

由式(12)、式(13)，对其进行求导，如式(14)所示

(14)

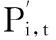
从上述分析知道通过对锚节点对未知节点影响的公式进行求导来判断权重修正系数是增加还是减小。锚节点自适应获得最优权重修正系数主要由以下3个阶段组成：

阶段1 锚节点加入网络可以得到锚节点的集合{B1,B2,B3…}，通过式(11)得到一组距离集合{d1,d2,d3…}。

通过以上3个阶段可以让锚节点自适应获得最优权重修正系数，从而不会造成因为静态的权重系数而造成的误差影响。在阶段3中，距离之差的阈值1.5m是通过阅读大量的参考文献得出的工程经验值。

2.3RSSI-DA-SWCL算法流程

1)无线传感网络节点组网

①网关节点组建网络，未知节点、锚节点申请加入网络。②未知节点向周围锚节点发送定位请求，并发送自身的位置信息。③锚节点发送应答帧，开始RSSI数据传输。

2)RSSI集合值优化

①未知节点接收各个锚节点发送的RSSI数据。②将大量RSSI数据按照RSSI测距优化算法进行整理，并按照式(11)计算距离结合{d1,d2,d3,d4,…}。

3)自适应取得最优权重修正系数

4)计算未知节点误差

(15)

3 仿真与实验

为了更好地验证RSSI-DA-SWCL算法的性能和可行性，分别进行了Matlab仿真和实测实验。

3.1Matlab仿真

选用MatlabR2010a作为仿真测试平台，网络定位区域为100m×100m；参考距离为1m处的功能损耗为0；定位区域初始化锚节点个数为20，并逐渐增加到90个；定位区域初始化未知节点为1个，并逐渐到10个；无线传感节点的通信半径为70m；高斯分布的均值为0，方差为1。路径损耗因子n为3；权重修正系数n在区间[1,4]内取得，初始权重修正系数为1.9。

3.1.1 锚节点数目对定位影响

如图5所示，当锚节点数目增加时，定位误差也减小，这是因为随着锚节点的密度不断增加，未知节点可利用的信息也就越多，RSSI值也就越准确，从而定位误差也就越小。在图5中，随着锚节点数目增加时，RSSI-DA-SWCL算法的定位误差整体要优于静态权重的定位误差。

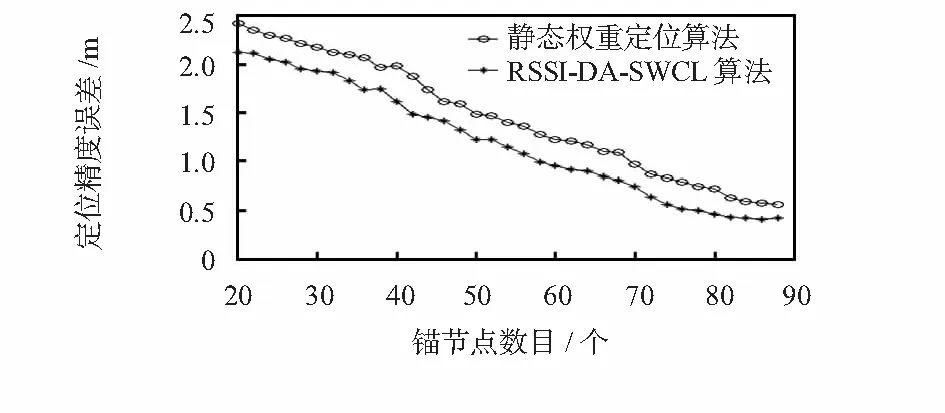
图5 锚节点数目对定位精度的影响

3.1.2 通信半径对定位影响

保持其它参数不变，锚节点个数为90个，未知节点数目为10个，仿真结果图如6。

图6 通信半径对定位精度的影响

当节点的通信半径增大时，未知节点可以利用锚节点的数目也就越多，未知节点可以利用更多的锚节点来修正自身的位置信息，从而定位精度也就越高。由图6可知，当通信半径增加时，RSSI-DA-SWCL算法的定位精度在整体上要优于静态权重定位算法。

3.2 实 验

利用TI公司的CC2520无线通信模块在井下巷道搭建小型的无线传感网络实验平台。具体实验参数设置：网络定位区域面积为2.5 m×13 m；节点通信半径为30 m；锚节点总数为12个；未知节点总数为6个；节点距离地面距离为1 m，实验次数为200次。

由表4可知，在井下巷道实际环境中，RSSI-DA-SWCL算法的最大误差为1.048 m，最小误差为0.781 m，平均误差为0.945 m，而静态权重算法的最大误差为1.142 m,最小误差为0.937 m,平均误差为1.05 m，RSSI-DA-SWCL算法比静态权重定位算法平均要低0.105 m,而且RSSI-DA-SWCL算法的最大误差和最小误差均要优于静态权重算法的误差。同Matlab软件仿真相比，其定位精度没有那么理想，这是由于在实际环境中由于受到路径损耗、多径效应等影响。但是RSSI-DA-SWCL算法的仿真实验和实测实验相差不是很大，基本上达到了预期的效果，同时也证明了RSSI-DA-SWCL算法的可行性。

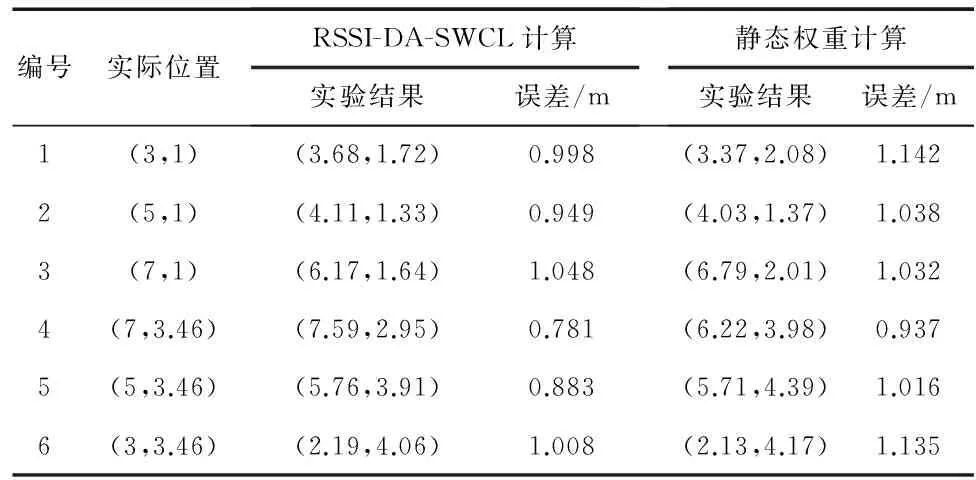
表4 井下巷道实验结果

4 结束语

针对静态权重定位算法固定的权重修正系数引起定位结果的误差的问题，本文提出了一种基于自适应权重定位RSSI-DA-SWCL算法。该算法将RSSI测距算法优化和让锚节点自适应获得最优权重修正系数，从而提高了定位精度。Maltab仿真和实测实验结果表明RSSI-DA-SWCL算法比静态权重算法有更高的定位精度，在实际环境具有可行性。

[1] Mainwaring A,Polastre J,Szewczyk R,et al.Wireless sensor networks for habitat monitoring[C]∥Proceedings of the1st ACM International Workshop on Wireless Sensor Networks and Applications,Atlanta,2002:88-97.

[2] Wang J,Ghosh R K,Sajal K D.A survey on sensor localiza-tion [J].Journal of Control Theory and Applications,2010,8(1):2-11.

[3] Zanca G,Zorzi F,Zanella A,et al.Experimental comparison of RSSI-based localization algorithms for indoor wireless sensor networks[C]∥Proceedings of the Workshop on Real-World Wireless Sensor Networks,ACM,2008:1-5.

[4] Wang J,Urriza P,Han Y,et al.Weighted centroid localization algorithm:Theoretical analysis and distributed implementation[J].IEEE Transactions on Wireless Communications,2011,10(10):3403-3413.

[5] 詹 杰,刘宏立,刘述钢,等.基于RSSI的动态权重定位算法研究[J].电子学报,2011(1):82-88.

[6] 吕 振,谭鹏立.一种基于RSSI校正的三角形质心定位算法[J].传感器与微系统,2010,29(5):122-124.

[7] 丁恩杰,乔 欣,常 飞,等.基于RSSI的WSNs加权质心定位算法的改进[J].传感器与微系统,2013,32(7):53-56.

[8] Zheng J,Wu C,Chu H,et al.Localization algorithm based on RSSI and distance geometry constrain for wireless sensor networks[C]∥2010 International Conference on Electrical and Control Enginee-ring(ICECE),IEEE,2010:2836-2839.

[9] 于海存.无线传感器网络加权质心定位算法研究[D].重庆：重庆大学,2014.

Adaptive weighted localization algorithm based on RSSI*

LIU Hong-li， ZHOU Deng， XU Kun， HU Jiu-song

(College of Electrical and Information Engineering，Hunan University，Changsha 410082，China)

Traditional static weighted centroid location(SWCL)cannot get accurate positioning precision because of influence of the multipath,reflection in indoor environment.Aimming at the problem,a new adaptive weighting positioning algorithm based on RSSI—DA—SWCL is proposed.The algorithm optimize the RSSI ranging method to eliminate the different node transmission power and other sudden interference effects on RSSI ranging.The algorithm use the information of anchor nodes and unknown nodes distance to dynamic let anchor nodes obtain the optimal weight coefficient adaptive,and it can improve positioning precision.RSSI—DA—SWCL algorithm is performed on the ZigBee platform,the RSSI—DA—SWCL algorithm performs better in terms of location precision by Matlab simulation and actual experiments compared to traditional localization algorithm.

wireless sensor networks(WSNs); dynamic weighted; centroid localization algorithm; RSSI ranging

10.13873/J.1000—9787(2017)03—0140—04

2016—04—08

国家自然科学基金资助项目(61172089)；湖南省科技厅资助项目(2012FJ4119)；中国博士后科研基金资助项目(2014M562100)；湖南省科技计划重点项目(2015JC3053)

TP 393

A

1000—9787(2017)03—0140—04

刘宏立(1963-)，男，教授、博士生导师，从事无线传感网络、移动通信系统和软件无线电的研究工作。