PSO-ELM的浆体管道临界淤积流速预测模型研究*

汪明先， 吴建德,2， 王晓东,2

(1.昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2.云南省矿物管道输送工程技术研究中心，云南 昆明 650500)

PSO-ELM的浆体管道临界淤积流速预测模型研究*

汪明先1， 吴建德1,2， 王晓东1,2

(1.昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2.云南省矿物管道输送工程技术研究中心，云南 昆明 650500)

针对浆体管道临界淤积流速预测难度大、精度低等问题，提出了粒子群优化—极限学习机(PSO-ELM)的临界淤积流速预测模型。利用PSO算法对ELM模型参数输入权值和隐元偏置进行优化，应用优化得到的ELM模型对预测集进行预测。通过实验仿真得到预测结果的最大误差为5.73 %，预测效果优于常规的ELM模型和反向传播(BP)神经网络模型。

浆体管道; 临界淤积流速; 粒子群优化算法; 极限学习机

0 引 言

近年来，浆体管道输送获得迅猛发展，已经成为第五大运输手段，是一种高效率、低成本、减少土地占用、无污染的固体物料输送技术[1]。然而，能否确定某一实际输送管道合适的临界淤积流速值直接关系到其能否安全运行，并在相同条件下能否取得最大的经济效益[2]。目前应用较多的浆体管道临界淤积流速预测方法有经验半经验公式法[3]、反向传播(back propagation,BP)神经网络法[4]和支持向量机(SVM)预测模型[5]，在某一程度上来说也获得了良好的效果，但其均有无法避免的缺陷，如经验公式往往考虑的因素比较单一，只适用于某些具体条件，由此导致计算出来的结果与实际所测得的数据之间有很大的误差；神经网络所需的数据量较大，经常会遇到过学习、陷入局部极值等问题[6]，在实际应用中为解决该问题，文献[7～9]提出了粒子群优化BP(particle swarm optimization,PSO-BP)算法、改进的BP算法用于研究多元有害气体的检测及传感器环境温度补偿问题，但其无法解决训练速度慢、预测效率一般等问题； SVM预测模型的参数选择较为复杂，从而严重影响了它的预测效率，文献[10]用人工鱼群算法优化SVM的惩罚参数和核函数参数，在一定程度上避免了参数选择的盲目性，提高了模型的识别精度，但仍然无法从根本上解决该问题。此时，极限学习机(extreme learning machine,ELM)预测模型[11]应运而生。

本文在前人实验研究的基础上，通过理论分析研究，确定了管道直径、粒料平均直径、物料密度与液体密度比和浆体体积浓度为影响浆体管道临界淤积流速的主要因素，建立将其作为输入因子，临界淤积流速值为输出因子的ELM预测模型，并针对ELM的不足，用粒子群算法对ELM中网络的输入层权值和隐单元阈值进行优选，进而提出了PSO-ELM模型对大直径浆体输送管道的临界淤积流速进行了研究。

1 材料与方法

1.1 临界淤积流速影响因素分析

从前人的实验中可以发现影响浆体管道临界流速的因素非常多，其中主要包括颗粒的大小、密度、形状、粒度分布、浆体浓度、管道运输直径、外部温度等等[12]。Duckworth 等人采用比水轻和比水重的物质分别进行了实验，观察到的实验现象为：在固体颗粒比水重的情况下，临界流速随着固体密度的加大而增大；在水比固体颗粒重的情况下，临界流速随着固体密度的减小而加快。通过浓度和临界流速关系Kazanskij公式可以总结出这样的结论：对于某一具体管径来说，通常情况下，浆体输送管道的临界淤积流速与浆体浓度呈正相关关系时，其浆体浓度处于低浓度范围；反之，但当浓度超过一定范围时，呈负相关关系，且易形成层流状态，阻力也快速增大。杜兰德公式[13]、Wasp公式[14]中均表明临界淤积流速与管径D的1/3方成正比，汪东等人根据试验数据绘制出临界流速与管径的次方关系图提出，在其他条件相同时，临界流速正比于管径的 1/3 次方[15]。浆体中颗粒在合理比例时，细颗粒间容易形成絮网结构，在阻尼作用的影响下，大大降低了粗颗粒的沉降速度，且不易形成滑、跳移状态，减少阻力损失。

基于以上分析可以看出，管道直径D、粒料平均直径d、物料密度与液体密度的比值S=ρs/ρ和浆体体积浓度Cv为影响淤积临界流速的主要因素。因此，浆体在水力固体运输管道中淤积临界流速可以表示为

(1)

1.2 基于PSO-ELM的预测建模

本文所提出的PSO-ELM算法，其基本思想是运用粒子群优化对单隐层前馈网络的输入层权值和隐元偏置进行优选，进而将其优选所得的输入权值和隐元偏置应用于浆体管道临界淤积流速的预测。算法的基本步骤如下：

1)随机产生种群：设定粒子的群体规模m，种群的个体维度D，该个体维度取决于ELM模型的输入参数，学习因子的初始值c1ini和c2ini，最大迭代次数kmax，实验结束条件最小误差。

4)粒子速度更新与位置更新：速度调整规则如下

(2)

5)全局求解最佳适应度：不断比较各粒子当前的适应度f(xi)与其历史最优适应度f(Pbest)，并结合结束条件确定其值大小。将结束的条件设置为寻优达到最大迭代次数kmax或评价值小于指定的精度,该精度设为0.001。

6)将最优解ai和bi代入ELM模型。

7)用测试数据对ELM进行训练，然后求解。

1.3 数据分析方法

采用均方根误差(RMSE)、决定系数(R2)、最大相对误差、平均相对误差等指标评价各模型计算结果与标准值之间的误差以及一致性，计算公式如下

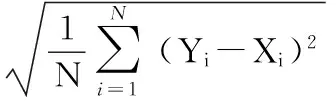
(3)

(4)

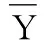
2 实验与分析

2.1 实验数据

结合国内外有关铁精矿、煤浆、硫精矿、磷精矿、电厂灰渣、尾矿等浆体管道整理得到的82组数据[17]，现将其中的77个样本构成训练集，用来进行ELM模型的训练，考虑到样本总体组成比较复杂和磷精矿管道实验数据过少等问题，故在测试数据的选取时，不考虑磷精矿，随机在其它 5类浆体管道中抽取5个样本作为测试数据，建立以管道直径、物料平均粒径、浆体体积浓度、物料比为输入因子，输出变量为临界淤积流速值 的ELM模型，对浆体管道临界淤积流速进行预测。

2.2 预测结果分析

假定隐含层节点数 ,在确定了ELM模型中的隐含层节点数后，采用PSO对模型隐含层输入权值ai和偏置向量bi进行优化选择，以确定最优的ELM模型。PSO的各参数如下：最大迭代次数kmax设为100，粒子数m设为20。最大惯性权重wmax取0.9；最小惯性权重wmin取0.4。学习因子c1初始值取1.68，c2初始值取1.3，学习因子c1,c2的最终迭代值c1fin和c2fin均取0.5。经PSO算法寻优后，得到最优适应度f(gbesti)=0.009 335,其对应的ELM参数ai,bi值即为最优参数，此时

a=

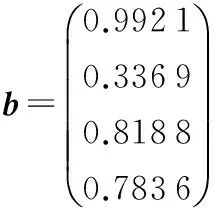
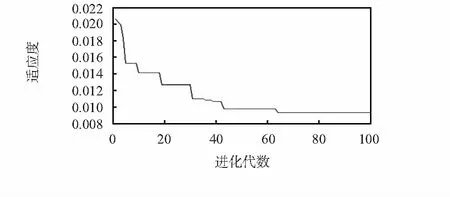
图1 适应度随迭代次数的变化曲线

根据优化得到的PSO-ELM模型对预测集进行预测，其预测结果及真实值与预测值之间的差值图如图2、图3所示。

从图2、图3可知，PSO-ELM模型的预测结果与真实值拟合效果较好，最大差值为0.085 2，且各差值在区间[-0.1 0.1]内波动，这说明PSO-ELM模型的预测值的误差是随机性的，不存在系统误差，也从侧面证明，本模型所选择的输入、输出参数是正确可行的。现将该模型与ELM模型、BP神经网络模型进行对比研究，利用上文中所确定的训练集、验证集对其进行训练，并产生预测结果，对比结果见图4及表1。

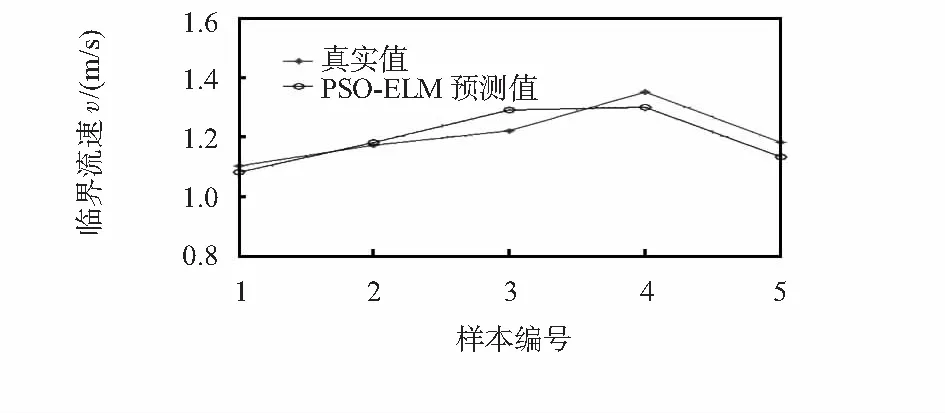
图2 真实值与预测值曲线图

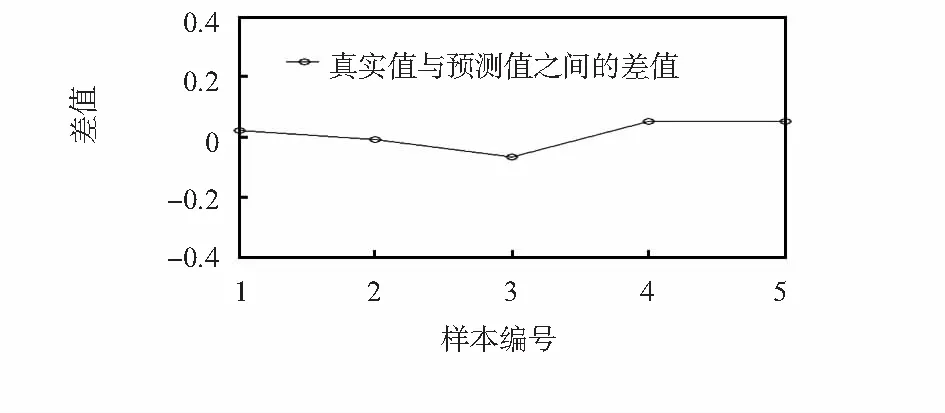
图3 真实值与预测值之间的差值图

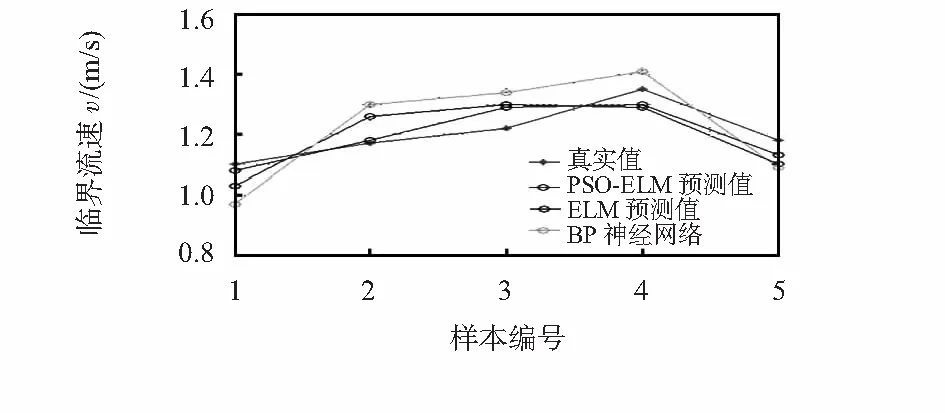
图4 三种模型的预测结果对比

由表1可以看出，采用PSO-ELM方法的5个样本中，相对误差最大值仅为5.73 %，小于ELM的最大相对误差7.69 %。与此同时，分析二者的误差可知，采用PSO-ELM方法得到的预测结果的相对误差与ELM相比均有相当程度上的减少，这说明运用PSO算法对优化ELM的输入权值和隐元偏置进行优选这一方法是可行的，所优选得到的输入权值和隐元偏置能够提高网络的泛化能力，进而能够提高该模型的预测精度。

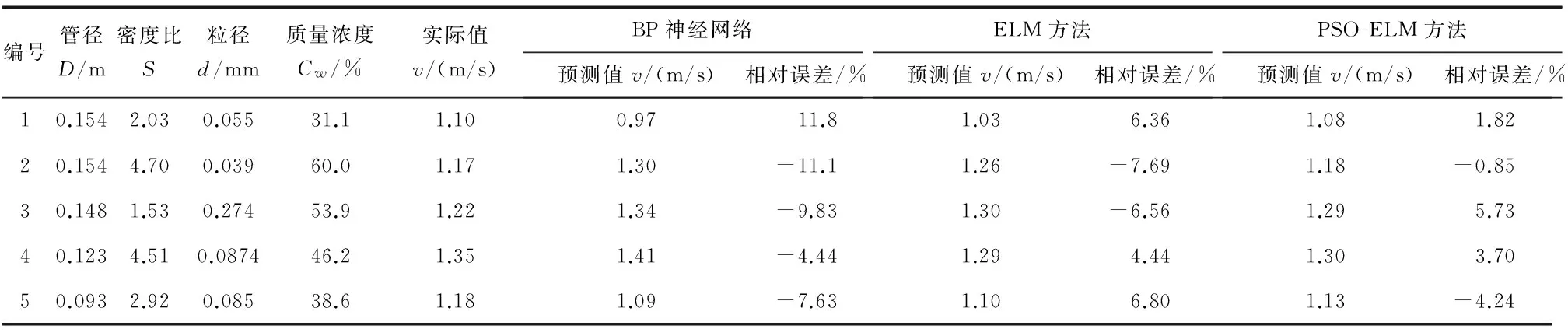
表1 临界淤积流速预测结果

2.3 模型精度比较分析

为显示本文所建预测模型的优势，定义RMSE、R2、最大相对误差、平均相对误差作为评价指标评价PSO-ELM模型、ELM模型、BP神经网络模型的计算结果的精度如表2所示。

从表2可以看出，BP神经网络模型由于样本数据少，临界淤积流速预测值误差大，最大误差可达11.8 %；PSO-ELM预测模型较常规的ELM预测模型预测精度更高，从模型决定系数R2分析可知，该模型吻合度更好，但在寻优过程中消耗了更多的时间。可见，本文提出的PSO-ELM模型方法在浆体输送管道临界淤积流速的预测方面较常规ELM模型有着更高的预测精度。

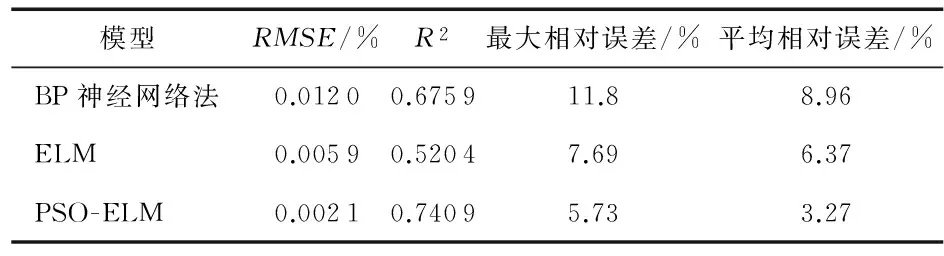
表2 几种模型预测结果评价指标比较

3 结束语

1)根据ELM原理，确定以管径、物料平均粒径、浆体体积浓度、物料比为输入因子，临界淤积流速值为输出因子，结合PSO，建立了PSO-ELM预测模型，避免了参数选择的随机性对模型精度的削弱。预测结果表明：PSO-ELM模型精度高，且误差在6 %以内。

2)利用BP神经网络和常规的ELM模型对结果进行预测，比较三者之间的预测效果，比较结果表明：PSO-ELM模型的预测精度要优于ELM模型和BP神经网络模型，PSO-ELM模型被证明是一种可行的临界淤积流速预测方法。

3)为进一步提高粒子群算法的全局搜索能力，减少无效迭代次数，以更快的速度求得最优适应度，拟对影响粒子群搜索性能的惯性权重优化进行深入研究，以期提出改进的PSO-ELM临界淤积流速预测模型。

4)利用粒子群算法对极限学习机的输入权值和隐元偏置的优选过程是一个随机过程，需要花费一定的时间，在后阶段将具体考虑如何用较少的时间来实现该优选过程。

[1] 费祥俊.浆体的物理特性与管道输送流速[J].管道技术与设备,2000(1):1-4.

[2] 费祥俊.浆体输送管道的不淤流速研究[J].煤炭学报,1997,22(5):532-536.

[3] Durand R.Basic relationships of the transportation of solids in pipes experiment[C]∥Research Proc Intern Assoc Hydr Res the 5th Congr,Minneapolis,1953:89-93.

[4] 韩 旭,张奇志,佟庆理,等.用人工神经网络法研究大直径浆体输送管道的淤积临界流速[J].中国有色金属学报,1997,7(4):26-29.

[5] 李 杰,楚 恒,朱维乐,等.基于支持向量机和遗传算法的纹理识别[J].四川大学学报,2005,37(4):104-108.

[6] 高海兵,高 亮,周 驰,等.基于粒子群优化的神经网络训练算法研究[J].电子学报,2004,32(9):1572-1574.

[7] 龚雪飞,徐 景,孙寿通,等.PSO-BP神经网络在多元有害气体检测中的应用[J].传感器与微系统,2015,34(2):154-156.

[8] 赵 斌,王建华.基于PSO-BP的红外温度传感器环境温度补偿[J].传感器与微系统,2015,34(2):47-49.

[9] 康国炼,杨遂军,叶树亮.改进BP算法在热流传感器温度补偿中的应用[J].传感器与微系统,2016,35(2):154-156.

[10] 洪 洁,王 璐,汪 超,等.基于人工鱼群算法优化SVM的手部动作sEMG识别[J].传感器与微系统,2016,35(2):23-25.

[11] Huang Guangbin,Zhu Qinyu,Siew Chee Kheong.Extreme learning machine:Theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[12] 汪 东,许振良,孟庆华.浆体管道输送临界流速的影响因素及计算分析[J].管道技术与设备,2004(6):1-2.

[13] Durand R.The hydraulic transportation of coal and solid materials in pipes[C]∥Colloq of National Coal Board,London,1952：39-52．

[14] Wasp E J,Kenny J P,Gandhi R L.Solid-liquid flow-Slurry pipeline transition[M].Rockport,MA:Trans Tech Publ,1977.

[15] 汪 东.非均质流水平管道临界流速研究[J].矿冶工程,2008(4):20-22.

[16] 王小川,史 峰,郁 磊,等.Matlab神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:243-255.

[17] 丁宏达.物料粒径对浆体管道输送临界流速的影响[J].水力采煤与管道运输,2011(4):1-6.

Study on prediction model of critical deposition velocity in slurry pipeline based on PSO-ELM*

WANG Ming-xian1, WU Jian-de1,2, WANG Xiao-dong1,2

(1.Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China; 2.Engineering Research Center for Mineral Pipeline Transportation of Yunnan,Kunming 650500,China)

Aiming at problems of great difficulties and low precision in predicting critical deposition velocity of slurry pipeline,a prediction model for critical deposition velocity based on particle swarm optimization and extreme learning machine(PSO-ELM)is proposed.The method using PSO algorithm to optimize the ELM model parameters such as the input weight and hidden element bias，the optimized ELM model is used to predict prediction set.The maximum error of predicted result is 5.73 % by experimental simulation,which shows that the prediction effect is superior to the conventional ELM and back propagation(BP)neural network model.

slurry pipeline; critical deposition velocity; particle swarm optimization(PSO)algorithm; extreme learning machine(ELM)

10.13873/J.1000—9787(2017)03—0066—04

2016—04—13

国家自然科学基金资助项目(51169007)；云南省科技计划项目(2013DH034)；云南省中青年学术和技术带头人后备人才培养计划项目(2011CI017)

TP 391; X 936

A

1000—9787(2017)03—0066—04

汪明先(1990-)，男，硕士研究生，研究方向为长距离浆体管道输送控制与智能控制算法研究。