互补滤波和卡尔曼滤波的融合姿态解算方法

张 栋， 焦嵩鸣， 刘延泉

(华北电力大学 自动化系，河北 保定 071003)

互补滤波和卡尔曼滤波的融合姿态解算方法

张 栋， 焦嵩鸣， 刘延泉

(华北电力大学 自动化系，河北 保定 071003)

针对捷联惯性测量单元(IMU)噪声大、精度低的缺点和常规的姿态解算算法精度不高等问题，提出了一种互补滤波和卡尔曼滤波相结合的融合算法。该算法基于姿态角微分方程建立系统的状态方程模型，利用互补滤波后的姿态角作为系统的观测量，再应用扩展卡尔曼滤波(EKF)算法融合了陀螺仪、加速度计和电子罗盘的测量数据。为验证该算法有效性，用带有传感器的开发板依次进行静态和动态测试，实验结果表明：结合了互补滤波和卡尔曼滤波的融合算法，在静态时能够抑制姿态角漂移和滤出噪声，在动态时能够快速跟踪姿态的变化，提高了姿态角的解算精度。

卡尔曼滤波； 互补滤波； 姿态估计； 数据融合； 惯性测量单元

0 引 言

随着微机电系统(MEMS)技术和计算机技术的不断发展，低成本的捷联惯性测量单元(inertial measurement unit,IMU)被广泛应用在小型飞行器中，捷联惯性测量单元由陀螺仪、加速度计和电子罗盘组成。陀螺仪受温漂的影响，长时间运行漂移严重，并且积分运算会产生累积误差；加速度计易受载体震动和运动加速度的影响；电子罗盘容易受外部磁场的影响[1]。因此,这三种传感器都不能单独用于飞行器姿态的测量，需要进行这三种传感器数据的融合。

被应用在飞行器姿态角上的数据融合算法有互补滤波[1～3]、共轭梯度法滤波[4]、扩展卡尔曼滤波[5～7](EKF)和无迹卡尔曼滤波[8～11](UKF)等。互补滤波原理简单，能够滤去噪声和抑制漂移，由于不容易确定合适的高通和低通截止频率，因此精度不高；文献[4]介绍了共轭梯度法滤波和互补滤波相结合在姿态解算中的应用，存在迭代计算量和精度的平衡问题；EKF和UKF是卡尔曼滤波对非线性系统的滤波方法，EKF存在线性化误差和截断误差，对一般的非线性系统影响不大；UKF在收敛速度和估计精度中要高于EKF，但其计算量要比EKF大，并且它们的系统噪声和观测噪声不容易确定，解算的姿态角容易受到噪声干扰。

本文提出的互补滤波与卡尔曼滤波相结合的融合算法，首先利用互补滤波把加速度计、电子罗盘和陀螺仪分别

解算的姿态角进行初步融合，滤去传感器噪声并抑制姿态角漂移，然后用互补滤波后的姿态角建立系统的状态方程和观测方程模型。因为模型的非线性特性，采用扩展卡尔曼滤波来提高姿态角的解算精度。

1 常规姿态解算方法

由于传感器不能直接测量飞行器的姿态角，姿态角需要捷联IMU测量的数据解算而来，姿态角既可由陀螺仪单独解算，也可以由加速度计、电子罗盘联合解算。

1.1 姿态描述

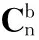
(1)

1.2 基于加速度计和电子罗盘的联合解算方法

加速度计和电子罗盘相互结合可以计算出三个姿态角，易知加速度计在导航坐标系n系下的矢量输出为[0 0 -g]T，由于

(2)

得到俯仰角和横滚角分别为

(3)

φ=tan-1(-ayb,-azb),φ∈(-π,π)

(4)

式中 [axbaybazb]T为加速度计在载体坐标系下的测量值。

偏航角需要借助上面计算出的俯仰角和横滚角来进一步计算得出。若电子罗盘在载体坐标系下的测量值为[mxb,myb,mzb]T，不考虑磁偏角影响，即将磁北作为真北，由

(5)

则地磁场在偏航角ψ、俯仰角θ和横滚角φ为0°的载体坐标系下的水平分量为

mx=mxbcosθ+mybsinθsinφ+mzbsinθcosφ

my=mybcosφ-mabsinφ

(6)

由于偏航角ψ北偏东为正，北偏西为负，所以,可以得到偏航角的解

ψ=-tan-1(my,mx),ψ∈(-π,π)

(7)

1.3 基于陀螺仪的欧拉角法

(8)

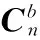
图1 补偿结构图

2 互补滤波和卡尔曼滤波的融合

加速度计和电子罗盘动态响应速度较慢，它们配合计算出的姿态角不能真实反映飞行器的姿态；陀螺仪解算的姿态角短时精度高，长期由于漂移和积分运算，计算的姿态角会产生累积误差。因此,需要将这两种姿态角进行融合得到精确的姿态角。

2.1 互补滤波

互补滤波就是用加速度计和电子罗盘解算的姿态角对陀螺仪解算的姿态角进行修正[3]，基本原理结构如图2，公式为式(9)

图2 互补滤波结构框图

(9)

式中 [φgθgψg]和[φamθamψam]分别为陀螺仪和加速度计、电子罗盘解算的姿态角，[φθψ]为融合后的姿态角。

k值的大小是基于合力加速度与重力加速度比值大小而定。比值过大或过小，说明加速度计计算的姿态角误差大，取消对陀螺仪计算的姿态角进行修正。比值处于规定区间，说明计算的姿态角是可靠的，可以修正

(10)

2.2 卡尔曼滤波

卡尔曼滤波算法是一种线性最小方差估计，是一种离散线性滤波的递推算法，它被应用在飞行器的姿态融合中，具有很高的姿态解算精度。飞行器中的卡尔曼滤波是利用传统姿态解算方法建立滤波模型，然后通过预测更新过程得到下一时刻的姿态角。

2.2.1 卡尔曼滤波状态方程和观测方程

为了实现卡尔曼滤波，应首先建立系统的状态方程和

观测方程。一般可选取三个姿态角参数作为状态空间模型的状态变量Xk=[φkθkψk]T，若系统的计算步距为T，由欧拉角法一阶离散更新方程得到卡尔曼滤波状态方程[13]为

Xk=f(Xk-1)+wk-1=

(11)

式中 [wφ(k-1)wθ(k-1)wψ(k-1)]T为系统噪声向量。

选取加速度计、电子罗盘联合解算的姿态角作为观测量Zk=[φamkθamkψamk]T，观测方程为

(12)

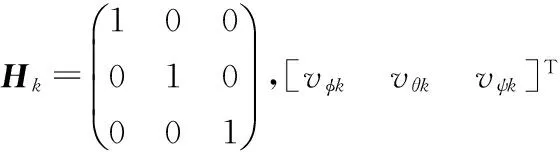
由于飞行器姿态滤波模型中的状态方程是非线性的，卡尔曼滤波基本方程不能直接解决非线性系统的滤波问题，可选择EKF解决系统的非线性。EKF是将模型的状态方程的非线性部分泰勒级数展开并取一阶近似，得到近似的线性化模型，然后再应用卡尔曼线性滤波。状态方程线性化求得的雅可比矩阵为

(13)

2.2.2 卡尔曼滤波算法流程

EKF的预测更新过程[6]如框图3。

图3 卡尔曼滤波流程图

1)状态一步预测

(14)

2)状态一步预测协方差矩阵

(15)

式中 P(k/k-1)为状态协方差矩阵P(k-1) 的估计，Q为系统噪声协方差矩阵。

3)卡尔曼增益更新

(16)

式中R为观测噪声协方差矩阵。

4)状态更新

(17)

5)状态协方差矩阵更新

P(k)=(I-K(k)Hk)P(k/k-1)

(18)

2.3 互补滤波和卡尔曼滤波的融合

观测量的选择对卡尔曼滤波很重要，选择观测量的误差大小影响卡尔曼滤波的效果，加速度计、电子罗盘直接解算的姿态角可以直接作为观测量，但是机体震动和外力加速度会给加速度计解算的姿态角很大的误差，因此，选择互补滤波融合后的姿态角作为模型的观测变量。两种算法融合的结构框图如图4。

图4 互补滤波和卡尔曼滤波结合的原理图

3 实验与结果分析

为了检验上述算法的可行性和有效性，选择了集成有处理器、陀螺仪、加速度计和电子罗盘的开发板，利用处理器采集传感器中的测量数据，通过串口将数据传送到上位机，利用Matlab软件用上述算法对其进行编程分析，比较滤波效果。

3.1 静态实验

将开发板放置在水平台面上，俯仰角和横滚角的理想值为0°，图5(a),(b),(c)分别为静态下分别用互补滤波、EKF、两者结合得到的横滚角，从图中可以看出，互补滤波后的姿态角有稍微的漂移，由于不能够准确估计观测量的噪声，导致EKF后的姿态角受到噪声干扰，两者结合滤波得到的姿态角能避免噪声干扰和抑制漂移。

图5 静态下的横滚角

3.2 动态实验

让开发板姿态变化时，用上述滤波算法分别滤波得到姿态角，图6(a),(b),(c)分别给出了互补滤波、EKF和两者相结合得到的俯仰角曲线。从图中可以看出：互补滤波得到的姿态角曲线能够跟踪姿态角的变化，但有一定的超调量，EKF滤波的姿态角动态响应慢，具有明显的滞后性，两者结合的滤波算法即能够滤除噪声，使姿态曲线更加平滑，又能在姿态变化较快时能够快速跟踪，且精度有所提高。

图6 动态下的俯仰角

4 结 论

经实验测试表明：两者结合的滤波算法对姿态角的漂移和噪声具有明显的抑制作用，在姿态角快速变化时能够实现快速跟踪，与互补滤波和卡尔曼滤波相比，能够明显提高姿态的解算精度。

[1] 梁延德.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011,30(11):56-58,61.

[2] 陈孟元.基于四元数改进型互补滤波的MEMS姿态解算[J].电子测量与仪器学报,2015,29(9):1391-1397.

[3] 张广玉,张洪涛,李隆球,等.四旋翼微型飞行器设计[J].哈尔滨理工大学学报,2012,17(3):110-114.

[4] 孙金秋. 基于共轭梯度法和互补滤波相结合的姿态解算算法[J]. 传感技术学报, 2014, 27(4): 524-528.

[5] 吴友强. 基于卡尔曼滤波的四旋翼飞行器悬停控制研究[J].自动化与仪表,2013(11):1-5.

[6] 汪 芳,朱少华,雷宏杰.基于卡尔曼滤波器的数字式捷联航姿系统算法设计[J].中国惯性技术学报,2008,16(2):208-211.

[7] 汪绍华.基于卡尔曼滤波的四旋翼飞行器姿态估计和控制算法研究[J].控制理论与应用,2013,30(9):1109-1115.

[8] 乔相伟.用四元数状态切换无迹卡尔曼曼滤滤波器估计的飞行器姿态[J].控制理论与控制应用,2012,29(1):97-103.

[9] 朱丰超.基于低成本陀螺和倾角仪的姿态估计[J].宇航学报,2011,32(8):1728-1733.

[10] Zhao Lin,Nie Qi,Guo Qiufen.Unscented Kalman filtering for SINS attitude estimation[C]∥IEEE International Conference on Control and Automation,2007:228-232.

[11] Pan Yue.Attitude estimation of miniature unmanned helicopter using unscented Kalman filter[C]∥International Conference on Transportation Mechanical and Electrical Engineering(TMEE),2011:1548-1551.

[12] 张 欣.多旋翼无人机的姿态与导航信息融合算法研究[D].长春:中国科学院研究生院,2015:43-44,63-65.

Fused attitude estimation algorithm based on complementary filtering and Kalman filtering

ZHANG Dong, JIAO Song-ming, LIU Yan-quan

(Department of Automation,North China Electric Power University,Baoding 071003,China)

Aiming at problem of high noise,low precision of inertial measurement unit(IMU)and low precision of classical attitude solution algorithm,a fused algorithm with complementary filtering and Kalman filtering is proposed.The algorithm establish the state equation model based on differential equation of attitude angle and choose attitude angle after compensation filtering as the observation of system.Use EKF algorithm fused measured data of gyro,accelerometer and electronic compass.To verify that the algorithm is effective, use development board with inertial sensors to test in static and dynamic condition.The results of experiments show that the algorithm fused with complementary filtering and Kalman filtering can constraint drift and noise of attitude angle in static condition and track change of attitude angle quickly in dynamic condition,thus precision of attitude angle estimation is improved.

Kalman filtering; complementary filtering; attitude estimation; data fusion; inertial measurement unit(IMU)

10.13873/J.1000—9787(2017)03—0062—04

2016—04—27

V 249

A

1000—9787(2017)03—0062—04

张 栋(1991-)，男，硕士研究生，主要研究方向为微型四旋翼飞行器的姿态和位置控制。