基于优化粒子群算法的无人机航路规划*

张建南， 刘以安， 王 刚

(1.江南大学 物联网工程学院，江苏 无锡 214122； 2.中国舰船研究院，北京 100192)

基于优化粒子群算法的无人机航路规划*

张建南1， 刘以安1， 王 刚2

(1.江南大学 物联网工程学院，江苏 无锡 214122； 2.中国舰船研究院，北京 100192)

针对粒子群优化(PSO)算法的无人机(UAV)航路规划问题，引入惯性权重和自然选择对粒子群算法进行优化，以提高基本粒子群算法收敛速度，防止陷入局部最优。算法分析惯性权重对粒子群算法的影响，进而调整惯性因子，提高算法的搜索能力；利用自然选择的便利性和规律性等特点,更新粒子群算法的粒子；同时通过对无人机的可行航向进行限定，缩小搜索范围。仿真实验表明:基于粒子群优化算法的无人机航路规划不仅缩短了最优航路，而且提高了搜索速度。

无人机航路规划； 粒子群优化算法； 惯性权重； 自然选择

0 引 言

近年来，随着科学技术的不断发展，无人机(unmanned aerial vehicle，UAV)作为控制侦察和作战的重要手段，正逐渐受到世界各国军方的关注，这促使科研人员对无人机的各个方面展开更深入的研究。无人机的航路规划是无人机任务规划的重要内容之一，目的是在满足燃料消耗、威胁以及飞行区域等约束条件下，为无人机规划出一条从初始点到目标点航路评价达到最优的飞行路线，以保证飞行任务的圆满完成[1]。

航路规划是一个空间搜索问题，受到国内外大量学者的研究，它主要分为两类：启发式算法和进化算法。启发式算法作为逐点搜索算法，其搜索空间庞大，计算量大，并且规划效果对启发函数的依赖性较强；进化算法是一种基于种群的优化算法，常用的进化算法有A*算法[2]、蚁群算-法[3]和遗传算法[4]等。这些算法自身都存在一定的缺陷，使得路径搜索存在搜索量大，效率不高等问题，不能保证航路规划设计的效率和要求。粒子群算法是智能算法的代表方法之一，是一种以随机搜索为特征的智能算法，通过群体粒子之间的合作与竞争产生的群体智能指导优化搜索，具有实现容易、精度高、方便调整参数等优点，因而在航路规划问题中得到了广泛的应用[5]。

粒子群算法思路清晰、运算简单、易于实现，广泛用于解决各种优化问题，但是也存在着早熟现象、收敛速度慢，过早陷入局部最优等缺点[6]。针对粒子群算法存在的问题，对粒子群算法进行了优化，使之适用于无人机航路规划。

1 无人机航路规划

1.1 飞行环境和任务规划

无人机航路规划问题实质属于最优化问题，它的数学描述由航路优化指标和航路约束条件两部分组成。求解航路规划问题，就是在满足约束条件的前提下，求出航路优化指标函数的全局最优解。航路规划的目的是要根据任务要求，威胁分布，燃料限制以及无人机自身的机动性能选择一条使无人机回避威胁，安全完成预定任务的飞行路径[7]，无人机在空中飞行区域如图1所示，其飞行任务是从O点飞行到A点，O点和A点之间存在威胁区，这些威胁可能是岛屿、陆地或者雷达，飞行航路就是搜索出一条从O点到A点的既短又安全的航路。

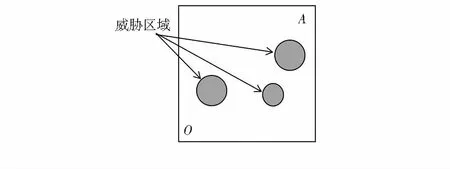
图1 无人机任务规划

1.2 编码方式

假设无人机在某一巡航高度匀速飞行，则航路规划可以简化为建立在二维平面环境的基础上[8]。先建立飞行高度相应的威胁平面分布，然后进行航路规划。建立笛卡尔坐标系，定义航路初始点和目标点，将起始点到目标点进行n+1等分，令航路点在各个边界上，这样每一维的次序表示了粒子在x方向上的位置，每一维的数据表示粒子在y方向上的位置。通过这样的方式，使每个粒子与起始点和目标点结合，这样就构成了无人机的一条航路[9]。

1.3 无人机航路规划代价模型

无人机的航路规划不仅要使无人机避开可能影响飞行的地形和威胁区域等不利因素，且要求规划出的航路优化指标最优，通常根据优化指标不同，航路优化分为不同的类型，包括以燃料消耗为指标的最大航程规划、以无人机飞行距离为指标的最短航程规划和以战术效果为指标的最优战术效果规划。本文主要考虑无人机的航程代价和威胁代价，其描述为

(1)

航路代价为各个航路段代价之和，设整个航路有n个航路段组成，j为威胁源的数量，li表示第i个航路段的长度，航程代价的作用是使飞机在降低油耗和缩短飞行时间的同时保证航路最短。在雷达参数保持一致的情况下，无人机在任务区域内的x处受到的第j个威胁源的威胁代价为[10]

(2)

在飞机飞行高度的水平截面上，雷达及区域威胁范围可近似看作一个圆，Rj表示无人机到区域中心的距离，Kj为第j个威胁的强度参数。采用如下方法处理：在每个航路段上取其两端点和中点三个点，分别求此三点受到的威胁体的威胁概率，则此航路段受到的威胁概率用这两点受到的威胁概率之和来表示。航路的威胁代价为各航路段威胁代价之和。式(1)中的w1，w2为权重系数，用以调整不同代价在航路代价中的权重。

2 基于粒子群算法的无人机航路规划

2.1 标准粒子群算法

粒子群算法是模拟鸟群随机搜寻食物的捕食行为，用于解决优化问题。在粒子群算法中每个优化问题的潜在解都可以想象成搜索空间的一只鸟，称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应度值，每个粒子还有一个速度决定它们的飞行的方向和距离。然后粒子就追随当前的最优粒子在解空间中搜索[11]。

粒子群算法初始化一群随机粒子，然后通过迭代找到最优解[12]。在每一次迭代过程中，粒子通过跟踪两个极值来跟新自己：第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。假设在一个d维的目标搜索空间中，有n个粒子组成一个群落，其中，第i个粒子为一个d维向量

Xi=(xi1,xi2,…,xid),i=1,2,…,n

第i个粒子的飞行速度也是一个d维向量，记为

Vi=(vi1,vi2,…,vid),i=1,2,…,n

第i个粒子迄今为止搜索到的最优位置称为个体极值，记为

Pbest=(pi1,pi2,…,pid),i=1,2,…,n

整个粒子群迄今为止搜索到的最优位置为全局极值，记为

gbest=(pg1,pg2,…,pgd)

在找到这两个最优值时，粒子根据式(3)、式(4)来更新自己的速度和位置

vid=w·vid+c1r1(pid-xid)+c2r2(pgd-xid)

(3)

xid=xid+vid

(4)

式中w为惯性权重，c1，c2为加速度因子，r1，r2为[0,1]中的均匀随机数[13]。

2.2 粒子群算法的改进

2.2.1 线性递减权重法

针对基本粒子群算法容易早熟及容易在全局最优解附近产生振荡现象，本文提出线性递减权重法，使惯性权重依照从大到小递减[14]，其变化公式为

(5)

式中wi为惯性权重最大值，wf为惯性权重最小值，t为当前迭代步数，tmax为最大迭代次数。

2.2.2 自然选择法

基于自然选择法是借鉴自然选择的原理，以提高粒子群算法的收敛速度，防止陷入局部最优，在每次迭代中，根据粒子群适应值将粒子排序，用群体中最好的一半粒子替换最差的一半粒子，同时保留每个个体所记忆的历史最优值。

2.3 路径优化

由于自身性能限制及使用条件，要求无人机在飞行过程中满足相应的约束，进行路径优化[15]。基本路径优化流程：限制航路长度必须小于预设的最大距离，减小搜索范围，规划不能超出搜索空间的范围，提高粒子群算法收敛速度；当无人机从某一个航路段向下一个航路段飞行时，受到无人机机动能力的限制，给无人机设置最大的拐弯角，规定其航向角不能超过45°，直到找到适合的航路[16]。

2.4 算法流程

1)任务区初始化，建立地形信息，初始化粒子群算法参数，包括群体规模n、每个粒子的位置Xi和速度vi，以及各项参数。

2)计算粒子适应度值，求全局最优粒子gbest，并将Pbest设置为每个粒子的当前位置。

3)根据速度和位置更新公式，更新每个粒子的速度和位置。

4)将每个粒子的适应值与粒子的最好位置比较，如果相近，则将当前值作为粒子最好的位置。比较当前所有的Pbest和gbest，更新gbest。

5)根据适应值对粒子群排序，用群体中最好的一半粒子替换最差的一半粒子，同时保留原来每个个体所记忆的历史最优值。

6)当算法达到其停止条件，则停止搜索并输出结果，否则,返回到步骤(3)继续搜索。

3 仿真验证

本文在Matlab 7.6环境下对无人机航路规划进行仿真，验证所提出的方法的有效性。任务区如图2,无人机起始位置(0,0)，目标点位置(500,0)，任务区有4处威胁区，如图中圆形区域所示。令终止迭代次数为1 000，粒子个数为200，粒子维数为10，加速度因子r1=r2=0.8，w=0.8，航程和威胁代价权重系数w1=w2=0.5，如图2所示,无人机需要从起始点绕过威胁区飞行到目标点。

图2 无人机航路规划任务区

图3和图4为基本粒子群算法航路规划图，如图所示，仿真结果最后收敛为286.92。图5和图6为优化粒子群算法航路规划图，根据式(5)更新惯性权重因子,设置w1=0.9，wj=0.4，在每次迭代结束时采用自然选择更新粒子，按照适应度值对所有粒子进行排序，用群体较好的50 %粒子代替较差的50 %粒子，更新粒子速度和位置，优化算法使得航路规划路线长度变短，路线趋向于平和，优化后的算法收敛到273.86，可以看出当改变惯性权重和采用自然选择优化粒子群算法时，收敛速度明显加快，同时相应地缩小了航路长度。所以改进方法得到了验证。

图3 基本粒子群算法航路规划结果

图4 基本粒子群算法适应值收敛图

图5 优化粒子群算法航路规化结果

图6 优化粒子群算法适应值收敛图

4 结束语

本文将优化粒子群算法应用于无人机的航路规划，利用改变惯性权重，调整惯性因子的方法，提高算法搜索能力，减小搜索空间，通过自然选择优化粒子群算法，提高算法收敛速度，防止陷入局部最优，避免了早熟收敛问题，缩短了航路长度。实验表明：基于优化粒子群算法的航路规划是一种相对有效和相对优越的方法。

[1] 田 伟.无人作战飞机航路规划研究[D].西安：西北工业大学,2007.

[2] 穆中林,鲁 艺,任 波,等.基于改进A*算法的无人机航路规划方法研究[J].弹箭与制导学报,2007,27(1):297-300.

[3] 姚永杰,席庆彪,刘慧霞.基于改进遗传蚁群算法的无人机航路规划[J].计算机仿真,2011,28(6):44-47.

[4] Fei S U,Hui P,Shen L C.Research on multi-UCAV cooperative route planning based on coevolutionary multi-ant-colony algorith-m[J].Binggong Xuebao/Acta Armamentarii,2009,30(11):1562-1568.

[5] Fu Y,Ding M,Zhou C.Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV[J].IEEE Transactions on Systems Man & Cybernetics Part A:Systems & Humans,2012,42(2):511-526.

[6] 王 波,王灿林,梁国强.基于粒子群寻优的D-S算法[J].传感器与微系统,2007,26(1):84-86.

[7] 胡中华,赵 敏,姚 敏.无人机三维航路规划技术研究及发展趋势[J].计测技术,2009,29(6):6-9.

[8] 翟彦蓉,黄 欢,张 申,等.改进粒子群优化算法在TDOA定位中的应用[J].传感器与微系统,2013,32(4):145-148.

[9] 张仁鹏,杨金孝,潘佳华,等.基于改进粒子群算法的无人机三维航迹规划[J].计算机仿真,2014,31(3):65-69.

[10] 李 猛,王道波,柏婷婷,等.采用威胁启发粒子群算法的无人机航路规划[J].电光与控制,2011,18(12):1-4.

[11] 胡中华,赵 敏.基于人工蜂群算法的无人机航迹规划研究[J].传感器与微系统,2010,29(3):35-38.

[12] Wang G,Li Q,Guo L.Multiple UAVs routes planning based on particle swarm optimization algorithm[C]∥2010 the 2nd International Symposium on Information Engineering and Electronic Commerce(IEEC),IEEE,2010:1-5.

[13] 杨 遵,雷虎民.采用粒子群优化算法规划无人机侦察航路[J].电光与控制,2007,14(2):4-7.

[14] 孙 湘,周大为,张希望.惯性权重粒子群算法模型收敛性分析及参数选择[J].计算机工程与设计,2010,31(18):4068-4071.

[15] 马传焱.多无人机飞行路径自动规划算法研究[J].无线电工程，2015，45(2)：5-7.

[16] 潘 杰.基于改进蚁群算法的移动机器人路径规划[J].中国矿业大学学报,2012,34(1):473-475.

UAV route planning based on PSO algorithm*

ZHANG Jian-nan1， LIU Yi-an1， WANG Gang2

(1.College of IOT Engineering,Jiangnan University,Wuxi 214122,China;2.China Ship Research and Development Academe,Beijing 100192,China)

Aiming at unmanned aerial vehicle(UAV)route planning problem of particle swarm optimization(PSO)algorithm,introduce inertia weight and natural selection to optimize PSO,in order to improve convergence speed of basic PSO,prevent fall into part optimum.Algorithm analyze on influence of inertia weight on PSO algorithm,and then adjust inertial factor,improve search ability of algorithm;Using characteristics of convenience and regularity of natural selection update particle of PSO;At the same time through limiting practical course of UAV,narrow search range.Simulation results show that,UAV route planning based on optimized PSO algorithm not only reduces the optimal route,but also improve search speed.

unmanned aerial vehicle(UAV); route planning; particle swarm optimization(PSO)algorithm; inertia weight; natural selection

10.13873/J.1000—9787(2017)03—0058—04

2016—04—25

国家自然科学基金资助项目(61170120)

TP 391

A

1000—9787(2017)03—0058—04

张建南(1991-)，男，硕士研究生，主要研究方向为信息对抗与系统仿真。