基于SQP算法的感应式磁力仪传感器结构优化设计

吕浩音，何江飞

(陇东学院信息工程学院，甘肃庆阳745000；2.北京航空航天大学宇航学院空间科学研究所,北京100083)

基于SQP算法的感应式磁力仪传感器结构优化设计

吕浩音1，何江飞2

(陇东学院信息工程学院，甘肃庆阳745000；2.北京航空航天大学宇航学院空间科学研究所,北京100083)

感应式磁力仪传感器安装于卫星舱外伸杆末端，为了避免在卫星发射过程中由于承受着严峻的力学载荷冲击而导致损坏，传感器结构需具备优异的力学性能。针对感应式磁力仪传感器的结构设计，基于SQP算法，结合有限元仿真分析和动力学灵敏度分析，以传感器刚度、强度、一阶模态频率等作为性能约束条件，以传感器质量作为目标函数，建立优化问题数学模型，不断优化传感器结构设计参数直至满足指标要求，这对实际工程应用中类似结构的优化设计问题具有一定的参考意义。

SQP算法；有限元分析；灵敏度分析；结构优化；传感器

在现代结构设计中，优化设计是一项十分重要的技术，在减轻结构重量、减少材料消耗和改善结构性能等方面有着良好的效果。结构优化设计的本质就是求极值问题，它以力学理论和数学规划理论为基础，以计算机技术为工具，对设计变量进行寻优决策的一种先进技术[1]。

目前国内外在结构优化设计方面有许多成熟的算法，大致可以分为：最优化准则法、数学规划法以及现代仿生学算法[2]。序列二次规划(SQP)算法将一般的约束优化问题转化为二次规划子问题，以子问题的解作为迭代的搜索方向，不断迭代，直至逼近最优解，SQP算法是一类具有超线性收敛速度的非常有效的方法，同时具有效率高、适应能力强以及可靠性好等一系列优点，在约束优化问题上有着广泛的应用。在结构优化中，合理有效地利用有限元法进行结构分析，利用灵敏度计算寻找影响较大的设计变量，可以提高优化效率，减少优化成本。本文基于SQP算法，结合有限元仿真分析和动力学灵敏度分析，对感应式磁力仪传感器结构进行优化设计[3]。

1 结构优化的理论基础

1.1 结构优化的基本流程

在结构优化设计中，针对特定的优化问题，我们首先需要确定优化问题的目标函数、设计变量、约束条件和收敛准则，建立合理的有限元数学模型，因为数学模型的好坏对结构优化的结果有着决定性的影响。

在数学模型形成以后，通过采用合适的优化算法去求解数学模型。根据收敛准则，判断所求的解是否为最优解。若不是，则进一步优化，反复迭代直至求得最优解。

本文结合有限元分析计算和灵敏度计算，对感应式磁力仪传感器结构进行优化设计，其基本的优化过程主要有以下几个主要步骤[4]：

(1)根据设计变量，建立初始结构优化有限元模型；

(2)进行有限元分析计算,灵敏度计算；

(3)确定优化模型的设计变量，定义目标函数、约束条件和收敛准则，形成优化数学模型；

(4)选择算法，求解优化模型，获得新的设计变量；

(5)判断是否收敛，收敛则优化结束。否则，根据新的设计变量建立有限元模型，再转步骤(2)。

1.2 灵敏度分析

灵敏度分析是指模型的结构性能对设计参数变化的敏感程度，通过高精度的灵敏度分析可以确定对优化目标函数和状态变量的影响较大的设计参数，并选择其作为优化模型的设计变量，给出正确的搜索方向，从而使结构迭代分析的次数减少，提高优化效率[5]。感应式磁力仪传感器结构拥有较多的设计参数，若是不加选择地全部作为优化模型的设计变量，将会产生巨大优化设计计算量，浪费资源和时间。

本文以频率灵敏度分析为例，简单介绍灵敏度分析基本原理。频率灵敏度分析就是分析结构频率对结构设计参数变化的敏感程度，表示为[6]：

(1)

其中，fr为第r阶固有频率，ai表示第i个设计变量。

频率灵敏度Sf的计算可以选用全局差分法、半解析法和基于有限元法的数值解析法，各类方法适用的情况也不同，这里不一一赘述。针对感应式磁力仪传感器的频率灵敏度分析计算，本文主要简单介绍基于有限元法的数值解析法。

结构的无阻尼自由振动的有限元微分方程为[7]：

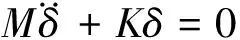
(2)

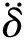
如果结构具有n个自由度，则可以通过求解式(3)来得到结构的n个特征值λr和对应的特征向量φr。

(3)

将式(3)对ai求偏导数，则有：

(4)

展开式(4)，得：

(5)

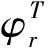
(6)

因为K和M为对称矩阵，并结合式(2)，则式(5)最后一项中的

(7)

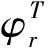
(8)

结合式(6)和(7)，由式(5)可得固有频率的灵敏度为：

(9)

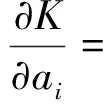
(10)

2 传感器结构优化设计

2.1 建立传感器初始模型

在感应式磁力仪传感器结构设计过程中，参考了以往有过飞行经历的传感器结构，如THEMIS、DEMETER等航天器上的空间低频交流磁场探测器，具体结构如图1和图2所示。

图1 THEMIS卫星低频磁场探测器

图2 DEMETER卫星低频磁场探测器

感应式磁力仪传感器结构在卫星发射过程中将承受着严峻的力学载荷冲击，对结构的力学性能有着严格的要求，根据卫星总体的设计输入条件和相关约束，初步设计感应式磁力仪传感器结构有限元模型，如图3所示。

图3 感应式磁力仪传感器有限元模型

通过模态分析、正弦振动试验仿真、随机振动试验仿真以及冲击试验仿真等有限元分析，初步检验传感器结构的力学性能。传感器结构的一阶模态频率为78.72Hz，应力响应最大值为62MPa。

2.2 建立数学模型

在感应式磁力仪传感器结构优化设计过程中，传感器的一阶模态频率和应力响应必须满足相应的指标要求：

fmin≥120Hz，σmax≤39MPa

故将传感器的基频和应力响应作为状态变量，并以传感器结构的质量作为目标函数[8]，即设计出符合力学性能要求的最轻量的传感器结构。

M=minf(X),X=[x1,x2,…,xn]T

其中M为传感器质量，X为设计变量。

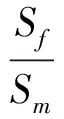
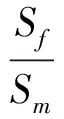
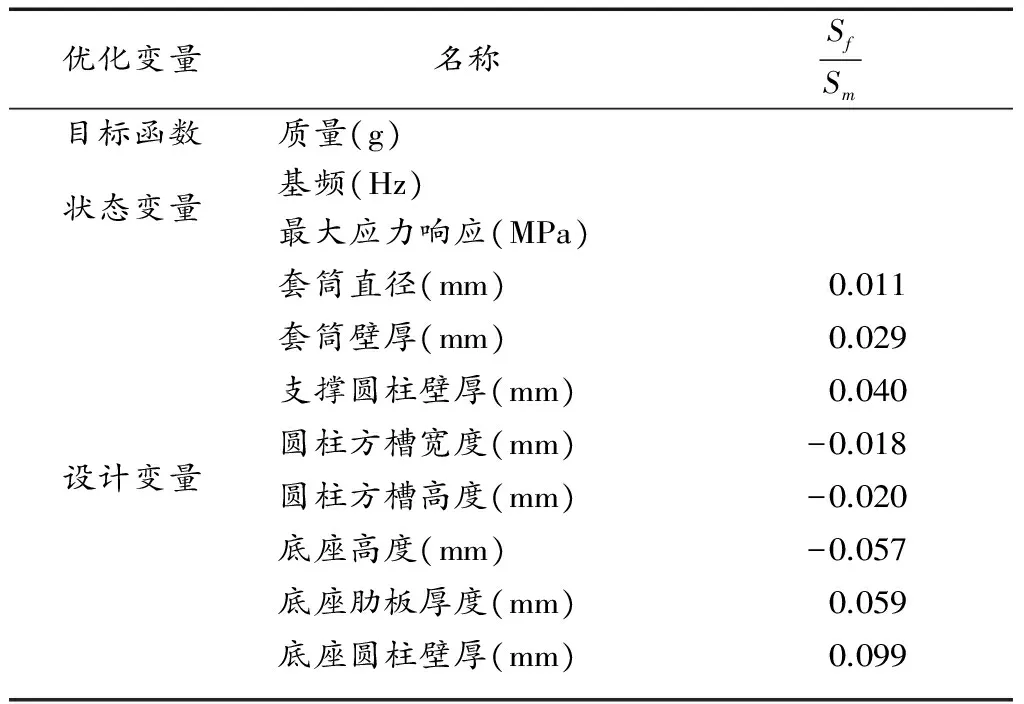
表1 优化模型的定义

2.3 优化算法

SQP算法将一般的约束优化问题转化为二次规划子问题，以子问题的解作为迭代的搜索方向，不断迭代，直至逼近最优解。具体表达式如下[9]：

(14)

其中x(k)为原问题的解，dk为二次规划子问题的解，ak为步长。在感应式磁力仪传感器结构优化过程中，有些约束是恒定的，而有些约束是在一定范围可变的，对于像这样带等式和不等式约束的优化问题：

minf(x)

s.t.gi(x)≤0,i=1,2,…,m,

hj(x)=0,j=m+1,…,m+l.

(15)

给定初始点x(0)∈Rn，初始对称正定矩阵B0，将上述优化问题其转换成相应的二次规划[10]

minz=

s.t.gi(x(k))Td+gi(x(k))≤0,i=1,2,…,m,

s.t.hj(x(k))Td+hj(x(k))=0,j=m+1,m+2,…,m+l.

(16)

由于二次规划(16)不易求解，利用该问题的最优性条件的近似分析，推导出二次子规划(17)

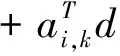
(17)

其中：

Pk=f(xk)-

dk是二次规划(16)的解，λk是相应的乘子。

为了确定算法的步长ak，定义函数φ(x)，ψ(x(k)+d)

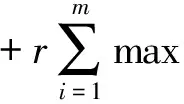
ψ(x(k)+d)=f(x(k))+

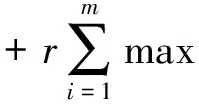
(18)

SQP算法的具体计算步骤如下[11]：

(3)若ρk<μ1，转步骤5，

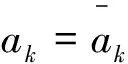
(6)修正Bk，得到新的对称正定矩阵Bk+1，令k=k+1，转步骤1。

2.4 优化结果

经过多次迭代优化后，利用最新的设计变量建立的有限元模型如图4所示。

图4 优化后的传感器有限元模型

优化变量名称初值下限值上限值优化结果目标函数质量(g)452．28380355．46状态变量基频(Hz)78．72120159．88最大应力响应(MPa)623936．51设计变量套筒直径(mm)23192422．4套筒壁厚2．51．532．2支撑圆柱壁厚(mm)1061210．5圆柱方槽宽度(mm)6287．3圆柱方槽高度(mm)1051311．6底座高度(mm)25153022．3底座肋板厚度(mm)2384．2底座圆柱壁厚(mm)2．51．532．2

在多次迭代优化的历程中，应式磁力仪传感器结构的质量、一阶模态频率、最大应力响应变化曲线分别如图所示，优化结果如表2所示。

图5 质量变化曲线

图6 一阶模态频率变化曲线

图7 最大应力响应变化曲线

最终，从图5，图6，图7可知，传感器结构质量优化到355.46g，比初值减少了21.4%；一阶模态频率优化到159.88Hz，提高了103.1%；最大应力响应值优化到36.51MPa，减少了41.1%，一阶模态频率fmin和最大应力响应σmax均满足指标要求。

3 结语

本文针对感应式磁力仪传感器的结构优化问题，结合有限元仿真分析和动力学灵敏度分析，建立了合理的传感器结构优化模型。利用序列二次规划(SQP)算法对传感器优化模型进行求解，优化模型的最优解使传感器结构的质量、一阶模态频率以及最大应力响应均得到了很大程度上的优化。优化结果表明：基于SQP算法同时结合有限元分析和灵敏度分析的结构优化方法高效可行，在实际工程结构优化应用中有较好的适用性。

[1]吕浩音.可训练文语转换系统的时长模型优化[J].计算机应用，2010,30(1):282-284.

[2]蔡新，李洪煊，武颖利，等.工程结构优化设计研究进展[J].河海大学学报，2011，39(3):269-274.

[3]毛虎平，吴义忠，陈立平.基于多领域仿真的SQP并行优化算法[J].中国机械工程，2009，20(15):1823-1829.

[4]DORNWS,GEMORYRE,GREENBERGHJ.Automaticdesignofoptimalstructures[J].JMech,1964,3(1):25-52.

[5]李越辉，尉庆国，徐彬，等.基于灵敏度分析的节能赛车车架轻量化设计[J].机械制造与自动化，2014,43(1):134-137.

[6]KIRSCHU,TOPPINGBHV.Minimumweightdesignofstructuraltopologies[J].JstrucEng,1992,118(7):1770-1785.

[7]姜成，赵又群，阮米庆，等.基于序列二次规划算法的机械弹性车轮的结构优化[J].机械科学与技术，2014，33(3)：423-427.

[8]BernardoHorowitz,SilvanaM.B.Afonso.QuadraticprogrammingsolverforstructuraloptimizationusingSQPalgorithm[J].AdvancesinEngineeringSoftware，2002，33(7)：669-674.

[9]赖炎连，贺国平.最优化方法[M].北京：清华大学出版社，2008:220-230.

[10]马迅，过学迅.基于有限元的结构优化与灵敏度分析[J].机械科学与技术，2002,21(4):558-561.

[11]梁醒培，王辉.基于有限元法的结构优化设计[M].北京：清华大学出版社，2010:109-110.

【责任编辑 朱世广】

Structural Optimization of the Induction Magnetometer Sensor Based on the Sequential Quadratic Programming Algorithm

LV Hao-yin1, HE Jiang-fei2

(1.SchoolofInformationEngineering,LongdongUniversity,Qingyang745000,Gansu; 2.SpaceScienceResearchInstitute,SchoolofAstronautics,BeihangUniversity,Beijing, 100083)

In order to protect the induction magnetometer sensor fixed on the end of a deployable boom of the satellite from the severe mechanical environment during the launching process, the induction magnetometer sensor should have sufficient stiffness and strength in structure. In this article, we combine finite element analysis and sensitivity analysis to establish a proper optimization model, making the stiffness, the strength and the first modal frequency of the sensor as the constraint conditions, the mass as the objective function. Based on the sequential quadratic programming algorithm, we resolve the problem until we get an optimal solution. The structural optimization of the induction magnetometer sensor can provide reference and basis for the structural optimization of other similar equipment.

SQP algorithm; finite element analysis; sensitivity analysis; structural optimization; sensor

1674-1730(2017)01-0015-05

2016-01-04

甘肃省档案科技项目计划《数字档案资料结构化管理方案研究》(2014-07)；2016甘肃省教育科学'十三五'规划《基于MOOC+SPOC平台的大学计算机翻转课堂应用实践研究》(GS[2016]GHB0242)

吕浩音(1976—),女,甘肃静宁人,副教授,硕士，主要从事计算机软件及应用研究。

TP212

A