序贯贝叶斯滤波估计模函数和水平波数

程泽丰，潘 翔

(浙江大学信息与电子工程学院，浙江 杭州 310027)

序贯贝叶斯滤波估计模函数和水平波数

程泽丰，潘 翔

(浙江大学信息与电子工程学院，浙江 杭州 310027)

介绍了一种在浅海波导环境中，联合声场模型和测量场，利用模基信号处理器解决非线性状态-参数估计问题的方法.在分析简正波模型表征声场的基础上，侧重研究了扩展卡尔曼滤波和粒子滤波两种算法，并将其用于模基水声信号处理进行声场参数估计.理论分析和数值仿真表明，两种算法均能正确估计模函数和水平波数，同时粒子滤波处理具有更好的宽容性.

序贯贝叶斯；粒子滤波；模基处理；水声波导

0 引 言

浅海环境是一个时变和空变的波导环境，水声信号在其传播表现为时延扩展和多普勒扩展.在波导环境中，通常用简正波模型来表征声场，用匹配场处理进行声源定位[1].由于理论模型和实际声场存在失配，宽容的匹配场处理成为研究的热点.

基于空间-状态模型的序贯贝叶斯滤波[2]适合在不确定的、非平稳和非高斯的变化环境中进行信号分析和处理，可以为模函数和水平波数的跟踪以及环境参数的反演提供有力工具.本文依据实际测量的声压场和声速剖面，基于简正模式传播模型，通过序贯贝叶斯滤波算法发展而来的基于扩展卡尔曼滤波[3](Extended Kalman Filtering, EKF)和粒子滤波(Particle Filtering, PF)的模基处理器，估计对应的模函数和水平波数.

1 空间-状态模型

运用序贯贝叶斯滤波处理海洋声信号增强问题，首先需要建立空间-状态模型.假设水平分层的海洋深度为h，已知声源水平距离rs和深度zs.由点声源发出的声能量用亥姆霍兹方程建模，经过标准的变量分离方法，获得只与深度相关的波方程表示方法

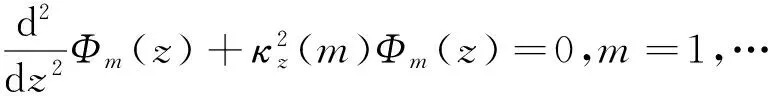
(1)

式中，本征解{Φm(z)}即所谓的模函数，κz为z方向上的垂直波数.同时对应的色散关系为

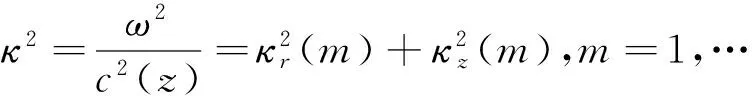
(2)

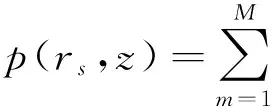
将只含深度参量的本征方程转化为状态-空间形式，将第m模式定义为

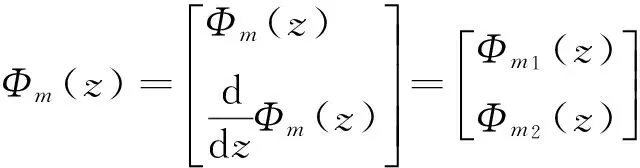
(3)

将噪声用加性噪声表示，并将确定的状态方程扩展为M个模式Φ(z)=[Φ1(z)|…|ΦM(z)]T以此导出模型的2M维的高斯-马尔可夫表示下的状态和测量方程

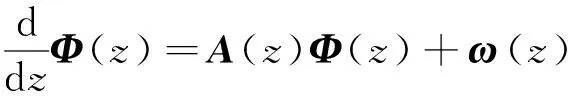
p(rs,z)=CT(rs,zs)Φ(z)+v(z),

(4)

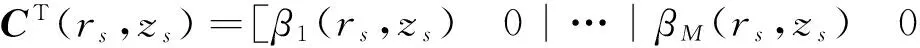
由于阵列在空间上以深度离散采样声压场，可以通过离散化微分方程来提高数值稳定性.假设传感器均匀分布，以zl表示第l个传感器所在的位置，得到

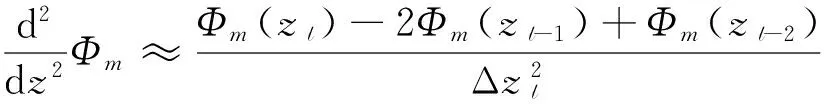
(5)

其中Δzl=zl+1-zl，将该近似方法代入式(1)，得到

Φm(zl)-2Φm(zl-1)+Φm(zl-2)+Δzl2κz2(m)Φm(zl-1)=0

将离散模态状态向量定义为Φm(zl)=[Φm(zl-2)|Φm(zl-1)]T，得到关于第m模式的一组差分方程.最后结合所有可能的模式，对简正模状态方程和测量方程的整体高斯-马尔可夫表示为

Φ(zl)=A(zl)Φ(zl-1)+ω(zl),

p(rs,zl)=CT(rs,zs)Φ(zl)+v(zl).

(6)

2 模基处理器

2.1 扩展卡尔曼滤波(EKF)

利用有限差分方法来离散化状态方程，导出第一节中所建立模型的离散形式

Φ(zl+1)=[I+ΔzA(zl)]Φ(zl)+Δzω(zl).

(7)

确立了高斯-马尔可夫模型，对状态向量Φ确定其递归(卡尔曼)估计器

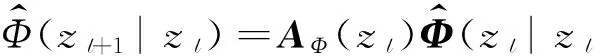
(8)

其中，AΦ(zl)=[I+ΔzA(zl)]，这种一般化表示方法，能够反映整个过程的递归本质.

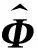
(9)

增益：卡尔曼增益由下式给出

(10)

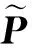
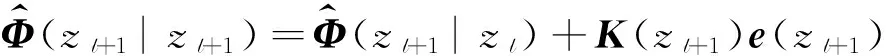
因此，在经过增强的高斯-马尔可夫模型中，非线性的测量方程可以写作

(11)

其中的c[·]的并非声速剖面c(z).需要得到增强的状态向量和相对应的测量中所有元素的一阶导数，构成整个系统的雅克比矩阵.

2.2 粒子滤波(PF)

扩展的卡尔曼滤波器基于泰勒级数的一阶展开，将非线性问题近似为线性问题.相比之下，粒子滤波则更加适合处理非线性问题.

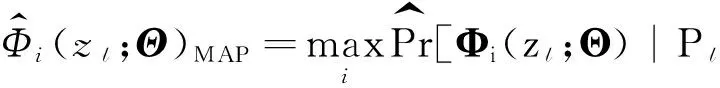
(12)

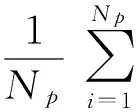
(13)

对应的状态和测量方程分别为

Φi(zl,Θ)=A(zl-1)Φi(zl-1)+ωi(zl-1),

p(rs,zl)=c[Φi(zl-1;Θ)]+v(zl).

(14)

3 仿真分析

3.1 仿真参数设置

图1详细给出了仿真环境参数的设定.图1左侧串状圆圈为接收阵，阵列的布放从水面以下深度10 m处开始，间隔Δzl=2.5 m设置阵元，一共有N=71个阵元，最后一个阵元放置在深度为185 m处的位置.图1中右侧标志为声源所在位置，离接收阵水平距离rs为0.5 km，深度zs为90 m，与垂直阵列中心位置等深，声源发出声信号的频率为50 Hz.将图1所示环境参数输入到简正模计算软件Kraken[4]中，所需要的垂直声速剖面如图2左图所示，计算获得的声压场如图2右图所示.

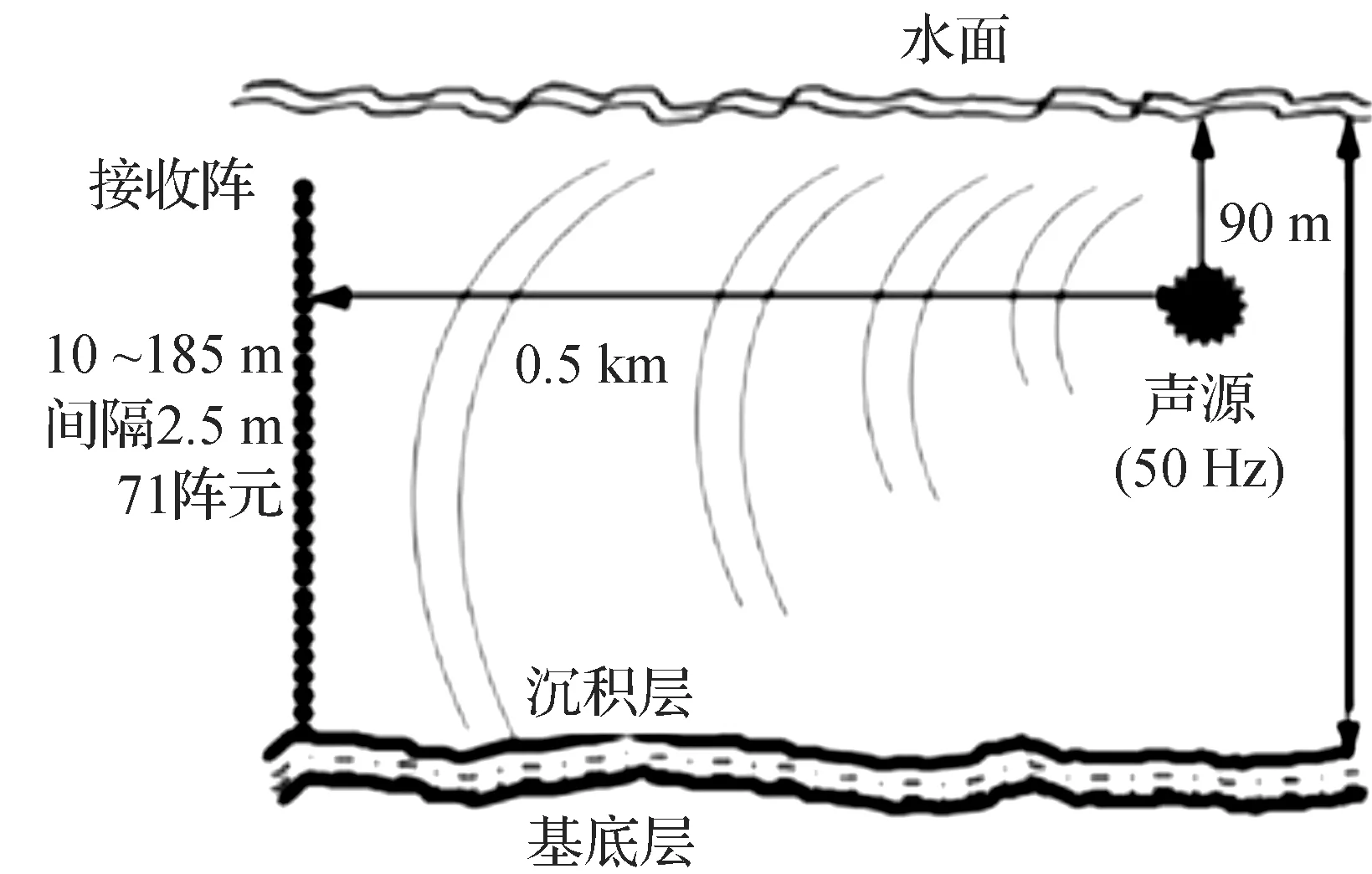
图1 仿真参数设置

图2 垂直声速剖面和声压场

图3给出了Kraken计算的结果，从左至右分别为1至8号模.

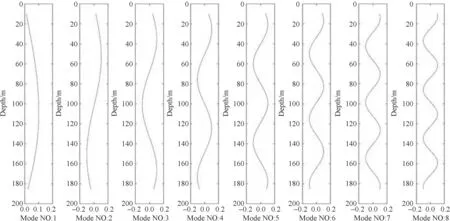
图3 Kraken计算得到的1至8号模

3.2 结果分析

通过Kraken计算，得到8个模式.图4给出分别利用EKF和PF模基处理器对第5号模模函数和水平波数的估计结果.图4(c)、图4(d)横轴表示水平波数，单位为m-1.

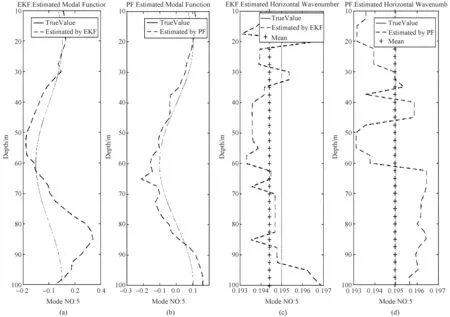
(a) EKF模基处理器估计模函数； (b)PF模基处理器估计模函数；(c) EKF模基处理器估计水平波数； (d)PF模基处理器估计水平波数图4 EKF和PF模基处理器估计结果

图4中，实线表示为真值，图4(a)中虚线表示EKF模基处理器对模函数的估计，图4(b)中虚线表示PF对模函数的估计结果.图4(c)和(d)中“+”号线分别为EKF和PF模基处理器对第5号模对应的水平波数的估计值.对第5号模而言，基于PF的模基处理器对模函数和水平波数的估计结果均优于基于EKF模基处理器，且MMSE在10-4数量级.分析其他模式，也存在类似的结论.表明了基于PF的模基处理器良好的宽容性.

4 结束语

在获得声速剖面和声压场数据的前提下，本文研究了表征声场的模函数和水平波数的估计问题.利用扩展的卡尔曼滤波器(EKF)和粒子滤波器(PF)构建了模基处理器，结合测量声压场和声速剖面联合估计模函数和水平波数.结果表明EKF算法在该问题上存在一定的局限性.而PF模基处理器，在设定的条件下，能够较为精确地估计模函数和水平波数，但其算法实时性远劣于前者.在今后的研究中，需要进一步检验PF模基处理器的宽容性.

[1]RISTICB,ARULAMPALAMS,GORDONN.BeyondtheKalmanFilter:ParticleFiltersforTrackingApplications[J].IEEETransofAerospace&ElectronicSystems, 2004, 19(7): 37-38.

[2]CANDYJV.BayesianSignalProcessing:Classical,ModernandParticleFilteringMethods[M].Hoboken,NewJersey, 2009: 369-417.

[3]CANDYJV,SULLIVANEJ.Model-basedIdentification:AnAdaptiveApproachtoOcean-acousticProcessing[J].IEEEJournalofOceanicEngineering, 1996, 21(3): 273-289.

[4]PORTERMB.TheKRAKENNormalModeProgram[R].SACLANTUnderseaResearchCentre,May17, 2001: 1-196.

[5]CANDYJV.EnvironmentallyAdaptiveProcessingforShallowOceanApplications:ASequentialBayesianApproach[J].JournaloftheAcousticalSocietyofAmerican, 2015, 138(3): 1268-1281.

Modal Function and Horizontal Wavenumber Estimation Using Sequential Bayesian Filters

CHENG Zefeng, PAN Xiang

(CollegeofInformationScience&ElectronicEngineering,ZhejiangUniversity,HangzhouZhejiang310027,China)

Combining acoustic pressure-field model and measurements based on model-based signal processing in shallow water waveguide, this paper introduces a solution to nonlinear state-parameter estimation problem. It focuses on the two algorithms, the extended Kalman filters and the particle filters, to estimate the parameters of acoustic pressure-field after analyzing the normal mode model representations of acoustic pressure-field. The theoretical analyses and the simulation results both show that the two algorithms are capable of estimating the modal functions and horizontal wavenumbers correctly. Meanwhile, the particle filter algorithm has a better robustness.

sequential Bayesian estimation; particle filter; model-based processing; underwater acoustic waveguide

10.13954/j.cnki.hdu.2017.01.011

2016-09-14

国家自然科学基金资助项目(61571397)

程泽丰(1993-)，男，浙江舟山人，硕士研究生，电子与通信工程.通信作者：潘翔副教授，E-mail: panxiang@zju.edu.cn.

TN929.3

A

1001-9146(2017)01-0046-05