关于3重量的二元线性码的一个注记

李明明，亓延峰，牛 刚

(杭州电子科技大学理学院，浙江 杭州 310018)

关于3重量的二元线性码的一个注记

李明明，亓延峰，牛 刚

(杭州电子科技大学理学院，浙江 杭州 310018)

布尔函数在密码学和编码理论中都有着重要的应用，由布尔函数构造的两类著名的二元码是Reed-Muller码和Kerdock码.该文考虑使用布尔函数来构造二元线性码，得到3重量的二元线性码，确定了此类二元码的参数和重量分布，此类小重量的线性码可以用于认证码、密码共享方案、结合方案和强正则图等.

线性码；重量分布；认证码；秘密共享方案；指数和

0 引 言

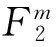
1 预备知识

给出基本符号定义，并给出线性码和指数和的相关结论，这些结论用于二元线性的参数和重量分布的确定.

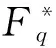
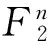
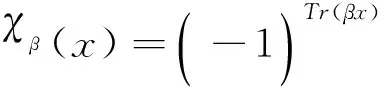
为了更好地计算构造的线性码参数，定义如下指数和

下面几个引理是关于指数和Sh(a,b)的一些结论.

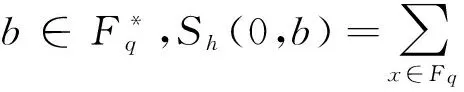
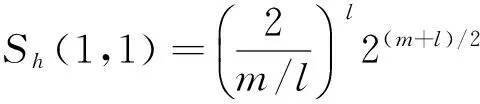
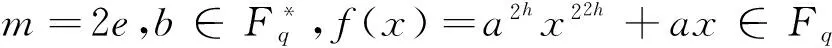
2 3重量的二元线性码

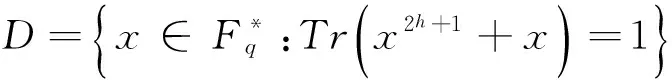
下面定理给出了线性码CD的具体参数和重量分布.

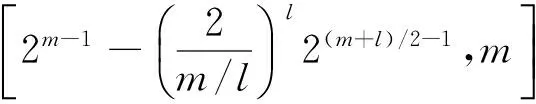
表1 线性码CD的重量分布

证明 为了得到线性码CD的参数和重量分布，定义如下参数

则码字cb=(Tr(d1x),Tr(d2x),…,Tr(dnx))的重量为n0-nb.

n0-nb=2m-2-Sh(1,1)/4+Sh(1,1+b)/4∈

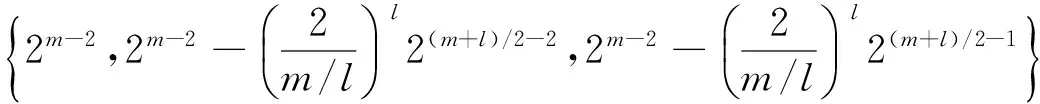
当m/l为偶数时，令m=2e.若m≡2 mod 4，由引理1.4知，Sh(1,1)=0，则线性码CD的码长为n=n0=2m-1.由引理1.1和引理1.4知，码字cb=(Tr(d1x),Tr(d2x),…,Tr(dnx))的重量为

若m≡0 mod 4，由引理1.4知，Sh(1,1)=-(-1)m/2l2m/2+l，则线性码CD的码长为n=n0=2m-1-Sh(1,1)/2=2m-1+(-1)m/2l2m/2+l-1.由引理1.1和引理1.4知，码字cb=(Tr(d1x),Tr(d2x),…,Tr(dnx))的重量为

n0-nb=2m-2-Sh(1,1)/4+Sh(1,1+b)/4∈

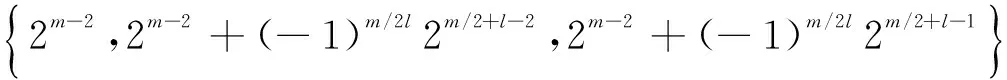
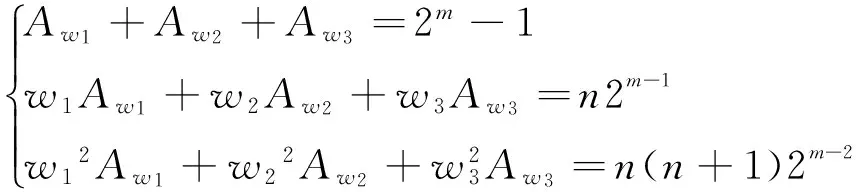
例2.1 设(m,h)=(5,1)，则l=1，m/l=5，由定理2.1得到线性码CD是参数为[20,5,8]的二元线性码，其重量计数为1+5z8+16z10+10z12.

例2.2 设(m,l)=(6,1)，则l=1，m/l=6，m≡2 mod 4，由定理2.1得到线性码CD是参数为[32,6,12]的二元线性码，其重量计数为1+6z12+47z16+10z20.

例2.3 设(m,h)=(8,1)，则l=1，m/l=8，m≡0 mod 4，由定理2.1得到线性码CD是参数为[144,8,64]的二元线性码，其重量计数为1+27z64+192z72+36z80.

3 结束语

本文结合文献[6]中线性码的构造方法，给出了一类3重量的二元线性码，并给出了二元线性码的相关参数和重量分布.文中的3重量二元线性码可用于结合方案的构造.未来的主要研究工作是寻找更多一般的函数构建好的小重量线性码并给出相关参数.

[1]DINGCS.Aconstructionofbinarylinearcodesfrombooleanfunctions[J/OL].ArXiv:1511.00321.2015,[2016-03-23].http://de.arxiv.org/pdf/1511.00321.

[2]YUANJ,DINGCS.Secretsharingschemesfromthreeclassesoflinearcodes[J].InformationTheory,IEEETransactionson, 2006, 52(1): 206-212.

[3]XIANGC.Linearcodesfromagenericconstruction[J].Cryptography&Communications,2015: 1-15.

[4]DINGKL,DINGCS.Aclassoftwo-weightandthree-weightcodesandtheirapplicationsinsecretsharing[J].InformationTheory,IEEETransactionson, 2015, 61(11): 5835-5842.

[5]ZHOUZC,LIN,FANCL,etal.Linearcodeswithtwoorthreeweightsfromquadraticbentfunctions[J].DesignsCodes&Cryptography, 2015: 1-13.

[6]TANGCM,LIN,QIYF,etal.Linearcodeswithtwoorthreeweightsfromweaklyregularbentfunctions[J].InformationTheory,IEEETransactionson, 2016,62(3):1166-1176.

[7]DINGCS.Linearcodesfromsome2-designs[J].InformationTheory,IEEETransactionson, 2015, 61(6):3264-3275.

[8]DINGKL,DINGCS.Binarylinearcodeswiththreeweights[J].InformationTheory,IEEETransactionson, 2014,18(11): 1879-1882.

[9]DINGCS,WANGXS.Acodingtheoryconstructionofnewsystematicauthenticationcodes[J].TheoreticalComputerScience, 2005, 330(1): 81-99.

[10]DINGCS,HELLESETHT,KLØVT,etal.Ageneralconstructionofauthenticationcodes[J].InformationTheory,IEEETransactionson, 2007, 53(6): 2229-2235.

[11]ANDERSONR,DINGCS,HELLESeETHT,etal.Howtobuildrobustsharedcontrolsystems[J].DesignsCodes&Cryptography, 1998, 15(2):111-124.

[12]CARLETC,DINGCS,YUANJ.Linearcodesfromperfectnonlinearmappingsandtheirsecretsharingschemes[J].InformationTheory,IEEETransactionson, 2005, 51(6):2089-2102.

[13]CALDERBANKARandGOETHALSJM.Three-weightcodesandassociationschemes[J].PhilipsJournalofResearch, 1984, 39(4):143-152.

[14]SPLLOYD.Hammingassociationschemesandcodesonspheres[J].SiamJournalonMathematicalAnalysis,1980, 1(3): 488-505.

[15]LIDIR,NIEDERREITERH.FiniteFields[M].Cambridge,U.K.:CambridgeUniversityPress, 1997:186-267.

[16]COULTER R S. On the evaluation of a class of Weil sums in characteristic 2[J]. New Zealand Journal of Mathematics, 1999, 28(2): 171-184.

[17]HUFFMAN W C and PLESS V. Fundamentals of Error-correcting Codes[M]. Cambridge, U.K.: Cambridge University Press, 2003: 259-262.

A Note on Three-weight Binary Linear Codes

LI Mingming, QI Yanfeng, NIU Gang

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Boolean functions have an important role in cryptography and coding theory. Two famous classes of binary codes constructed from Boolean functions are the Reed-Muller codes and Kerdock codes. This paper considers the construction of binary linear codes from Boolean function, presents a class of three-weight binary linear codes, and determines parameters and weight distribution of these codes. Binary linear codes with few weights can be applied in authentication schemes, secret sharing schemes, association schemes and strongly regular graphs.

linear codes; weight distribution; authentication codes; secret sharing schemes; exponential sums

10.13954/j.cnki.hdu.2017.01.021

2016-03-23

国家自然科学基金资助项目(11531002,11501154)

李明明(1991-)，男，山东德州人，硕士研究生，密码学.通信作者：亓延峰讲师，E-mail：qiyanfeng07@163.com.

TN911.22

A

1001-9146(2017)01-0095-04