混合整数非线性规划的自适应变异差分进化算法

车林仙， 何兵， 刘永波

混合整数非线性规划的自适应变异差分进化算法

车林仙1,2， 何兵2,3a， 刘永波3b

(1.重庆工程职业技术学院机械工程学院, 重庆402260;2.人工智能四川省重点实验室, 四川自贡643000;3.泸州职业技术学院a.机械工程系;b.信息工程系, 四川泸州646005)

提出了一种求解混合整数非线性规划(Mixed integer nonlinear programming，MINLP)的混合差分进化(Differential evolution，DE)算法。为提高DE算法的优化性能，设计了混沌初始化种群、可平衡全局探索与精细开采能力的混合变异版本、基于种群进化停滞代数记录的自适应二次变异算子等新型策略。将前述策略融入DE算法，形成面向MINLP的自适应变异差分进化(Adaptive mutation differential evolution，AMDE)算法。6个MINLP数值实例的对比实验表明了新算法的有效性和可靠性。最后，应用AMDE算法求解齿轮传动体积最小化工程优化设计实例，显示了该算法的工程应用价值。

混合整数非线性规划；差分进化算法；人工蜂群算法；自适应变异；齿轮传动优化设计

引言

工程设计、系统工程和经济管理等领域存在许多混合整数非线性规划(Mixed integer nonlinear programming，MINLP)问题，它同时包含连续变量和整数变量，其目标函数和约束条件通常呈现强烈非线性。MINLP的求解方法主要有两类。一类为确定性方法[1]，如分支定界算法、外逼近算法、割平面算法和广义Bender分解方法等混合变量规划方法。但这类方法的求解过程通常较复杂，并且对数学理论基础有较高要求。另一类为智能优化算法，如遗传算法(Genetic algorithm，GA)、进化策略(Evolution strategy，ES)、粒子群优化(Particle swarm optimization，PSO)算法和差分进化(Differential evolution，DE)算法等。

很多学者针对MINLP，提出了多种智能优化方法。张甲江等[2]、谭跃等[3]分别提出适于MINLP的量子粒子群优化算法和基于交叉与多混沌策略的粒子群优化算法。张莉等[4]、邓长寿等[5]、谭跃等[6]和摆亮等[7]先后设计多种面向MINLP的混合差分进化算法，如嵌入正交杂交算子的差分进化算法[4]、交替变异版本的差分进化算法[5]、混沌局部搜索差分进化(DE with chaotic local search strategy，CLSDE)算法[6]和差分进化分布估计混合算法[7]。文献[2-6]仅进行了经典函数优化问题测试，并未给出工程应用实例。因此，面向MINLP的智能算法，尚未在工程优化领域显示出应用价值。

为提高DE算法求解MINLP的精度和可靠性，本文提出一种自适应变异差分进化(Adaptive mutation differential evolution，AMDE)算法。该算法采用混沌序列初始化种群，融合人工蜂群(Artificial bee colony，ABC)算法[8-10]搜索方式和动态调整变异概率的二次变异，并采用可行性规则[11]处理约束条件。最后，应用AMDE算法求解6个MINLP数值实例和1个二级斜齿圆柱齿轮传动优化设计案例，得到了满意结果。

1 MINLP数学模型描述

不失一般性，将最小化MINLP问题表示为

(1)

式中，x为连续决策变量，x=(x1,x2,…,xD1)T；y为整数决策变量，y=(y1,y2,…,yD2)T；xU,d,xL,d为各维连续决策变量的上、下界；yU,d,yL,d为各维整数决策变量的上、下界；D1,D2为连续、整数决策变量的维数；f(x,y)是目标函数；gi(x,y)为不等式约束；hi(x,y)为等式约束；I1,I2为不等式、等式约束数。

为便于叙述，将决策矢量(x,y)统一记为混合整数决策矢量：

z=(z1,z2,…,zD1+D2)T= (x1,x2,…,xD1,y1,y2,…,yD2)T

并将z的各维分量上下界记为zU,d和zL,d(d=1, 2, …,D1+D。

应用DE算法求解MINLP式(1)时，涉及候选解(个体)比较与选择，本文应用Deb提出的可行性规则[11]比较两个候选解。该规则为：(1)任何可行解都优于不可行解；(2)对于两个可行解，目标函数值较小者为优；(3)对于两个不可行解，约束违反度较小者为优。为此，将任意候选解z的约束违反度函数fvio(z)定义为：

2 混合变量AMDE算法

DE算法的4个控制参数为：种群规模NP，缩放因子F，交叉因子CR和最大进化代数tmax。

应用DE算法求解式(1)时，将进化至第t代的第n个个体编码记为：

t=0, 1, …,tmax；n=1, 2, …,NP

2.1 混沌初始化

Kent映射生成的混沌序列分布均匀，且具有良好遍历性，本文应用该混沌序列生成初始种群。一维Kent映射可表示为：

d=1, 2,…,D1+D2；k=0, 1, …，NI

(2)

式中：μ0∈(0, 1)，为常数，且μ0≠0.5，本文取μ0=0.4；q0,d为(0, 1)内服从均匀分布的随机量，且满足q0,d≠μ0；NI为混沌序列个数。

由式(2)生成NI个(D1+D维混沌序列点之后，再按下式载波为NI个初始个体

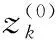
在NI个初始个体中，应用Deb规则选择较优的NP个体作为初始种群。

2.2 自适应变异概率

基本DE算法的种群多样性将随进化代数的增大而降低，求解某些多极值MINLP问题时，可能出现进化停滞和早熟收敛现象。为增强算法的全局优化能力，克服该缺陷，有必要对新生成的试验个体执行二次变异操作。当连续停滞代数较小时，宜设置较小的变异概率，避免过多无用操作而降低搜索效率；当连续停滞代数较大时，宜增大变异概率，利于保持种群多样性，增大获得全局最优解的概率。

定义1对于足够小的精度阈值δ(t)(随进化代数改变)，若满足

(3)

或

(4)

则认为种群在第t代进化停滞。根据实践经验，取δ(0)=10-5，δ(t)=δ(t-1)/1.035时，效果较理想。

若连续两代的最优个体均为可行解，则按式(3)判断；若连续两代的最优个体均为不可行解，则按式(4)判断；若连续两代的最优个体分别为不可行解和可行解，则认为种群在第t代进化未停滞。

算法设置计数器tst记录种群连续停滞代数，随着tst的变化，自适应调整变异概率pm，其计算式为：

(5)

由式(5)可知，当tst较小时，pm也较小；当tst增大时，pm也随之增大，但最大不超过0.1。因pm过大，将加大随机搜索成分，反而降低搜索效率。

2.3 计算流程

计算流程各步骤及生成新解时，参照2.1节。

(1) 初始化

(2) 变异操作

DE算法的关键在于先应用差分算子生成变异个体，再执行交叉操作生成试验个体。应用DE/rand/1策略生成变异个体时，算法具有较强全局探索能力，但局部精细开采能力偏弱。为提高收敛速度和精度，本文借鉴文献[10]中改进ABC算法的引领蜂搜索方式，引入一种基于最优个体的变异策略，记为DE/ rand/best-rand。该策略仍以随机个体为基向量，但差分向量指向最优个体，有利于精细开采且不易陷入局部最优区域。为了在全局探索和精细开采之间取得平衡，本文算法每次生成变异个体时，均在上述两种策略中随机选择一种。现将两种策略的变异算子描述如下：

(i) DE/rand/1策略

(6)

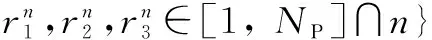
(ii) DE/rand/best-rand策略

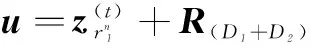
式中，R(D1+D为 (-1, 1)内服从均匀分布的(D1+D维随机数；⊗表示点对点乘法运算符。

若u之某维分量越界，则在其取值区间内随机生成该维分量。

(3) 交叉操作

式中，rand( )表示(0,1)内服从均匀分布的随机数；dr为随机自然数，且dr∈[1,D]∩Z；CR为交叉因子，且CR∈[0,1]。

(4) 二次变异操作

式中，M(·)为二次变异算子。

为增强算法的适应性，文中对连续变量和整数变量，分别执行非均匀变异和均匀变异操作。即，当vd(d=1, 2,…,D1)为连续变量时，二次变异算子为：

式中，r表示在(0,1)内服从均匀分布的随机数。

当vd(d=D1+1,D1+2,…,D1+D为整数变量时，又分为两种情形：若为0-1整数规划问题，二次变异算子为：

M(vd)=1-vd

若为一般整数规划问题，二次变异算子为：

M(vd)=zL,d+round[rand( )·(zU,d-zL,d)]

(5) 选择操作

对n=1,2,…,NP，重复执行NP次步骤(2)～(5)。

(6) 更新最优个体

(7) 终止判断

2.4 计算复杂度

可据第2.3节的计算流程分析AMDE算法的计算复杂度。步骤(1)的计算复杂度为O(NID)，步骤(2)～(4)的计算复杂度均为O(NPD)；步骤(5)的计算复杂度为O(NP)；步骤(6)的计算复杂度：搜索NP个个体中的最优个体为O(NP)，更新连续停滞代数计数器为O(1)。求和并忽略低阶项，可求得AMDE算法的计算复杂度为O(NPDtmax+NID)。算法独立运行1次的函数评价次数为NI+NPtmax。

3MINLP算例测试

3.1 测试实例

以下6个测试实例均引自文献[6]。

P1：minf(x,y)=2x+y

s.t.g1(x,y)=1.25-x2-y≤0

g2(x,y)=x+y-1.6≤0

0≤x≤1.6，y∈{0,1}

已知最优解(x,y;f*)=(0.5, 1; 2)。

P2：minf(x,y)=2x-ln(x/2)-y

s.t.g(x,y)=-x-ln(x/2)+y≤0

0.5≤x≤1.4，y∈{0,1}

已知最优解(x,y;f*)=(1.375, 1; 2.124)。

P3：minf(x,y)=5(x1-0.5)2-0.7y+0.8

s.t.g1(x,y)=-exp(x1-0.2)-x2≤0

g2(x,y)=x2+1.1y+1≤0

g3(x,y)=x1-1.2y-0.2≤0

0.2≤x1≤1，-2.22554≤x2≤-1，y∈{0,1}

已知最优解(x,y;f*)=(0.94194, -2.1, 1; 1.07654)。

P4：minf(x,y)=

s.t.g(x,y)=

0≤x≤10，y∈{0,1}

已知最优解(x,y;f*)=(3.51424, 1; 99.23964)。

P5：minf(x,y)=(x1-1)2+(x2-2)2+(x3-3)2+

(y1-1)2+(y2-1)2+(y3-1)2-ln(y4+1)

s.t.g1(x,y)=x1+x2+x3+y1+y2+y3-5≤0

g3(x,y)=x1+y1-1.2≤0

g4(x,y)=x2+y2-1.8≤0

g5(x,y)=x3+y3-2.5≤0

g6(x,y)=x1+y4-1.2≤0

0≤x1≤1.2，0≤x2≤1.8，0≤x3≤2.5

y1,y2,y3,y4∈{0,1}

已知最优解(x,y;f*)=(0.2,1.280624,1.954483,1,0,0,1;3.557463)。

37.29329y1+40792.141

s.t.g1(x,y)=a1+a2x3y2+a3x2y1-a4x1x3- 92≤0

g3(x,y)=a9+a10x1x3+a11x1y1+a12x1x2-25≤0

27≤x1,x2,x3≤45，y1∈[78,102]∩Z，

y2∈[33,45]∩Z

已知最优解(x,y;f*)=(27,*,27,78,*;32217.42778) (*表示最优解不确定)。对应系数取值见表1 。

表1P6中的系数取值

3.2 实验设置

AMDE算法控制参数：NP和tmax取值见表2 ，NI= 100NP，F=0.5+ 0.05rand( )，CR=0.9。

表2 AMDE算法的控制参数

为考察AMDE算法求解测试实例的优化性能，文中还以PSO算法，人工蜂群(Artificial bee colony，ABC)算法[11-12]和基本DE算法(第2.3节的算法流程中，步骤(2)仅用式(6)生成变异个体，且不执行步骤(4))等作为对比算法，进行比较分析。

为公平起见，3种对比算法均采用与AMDE算法相同的初始化、约束函数、取整和越界处理方法；对比算法的NP和tmax均与AMDE算法一致。DE算法的F,CR与AMDE算法一致。

PSO算法的惯性权重w线性递减，取w=1.2～0.2，加速度系数为c1=c2=2，最大速度取vmax,d= 0.3(zU,d-zL,d) (d=1, 2, …,D1+D。

ABC算法的引领蜂和跟随蜂各占种群规模的50%；跟随蜂采用2元锦标赛方法选择被跟随的引领蜂；引领蜂和跟随蜂执行邻域搜索生成新蜜源时，均以概率CR随机改变多维分量。

3.3 实验结果

4种算法分别独立运行50次的统计结果见表3 。其中，fb,fav,fw和σf分别表示最优目标函数值的最好、平均、最差值及标准差。同时，将CLSDE算法[9]的性能指标也列入表5 ，以便比较。

表3 5种算法求解实例的性能指标

为了便于应用对数坐标清晰显示各种算法的收敛精度，首先给出关于算法种群最小误差的概念。

定义2设待求MINLP问题的理论最优目标函数值为f*，定义第t代种群的最小误差为：

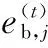
4种算法的平均最小误差eb,av(图中取对数)进化曲线对比如图1 所示。

由表3 和图1 可知，求解P1、P4、P5和P6时，PSO算法的eb,av最大，求解P2和P3时，PSO算法的eb,av与DE算法相当，但大于ABC和AMDE算法；求解6个实例时，PSO算法的σf均最大，稳健性最差。在5种算法中，PSO算法的优化性能最差。AMDE与ABC算法比较，求解P1、P2、P4和P6时，2种算法相当；而求解P3和P5时，AMDE明显优于ABC算法。AMDE与DE算法比较，求解P1、P4和P6时，2种算法相当；求解P2和P3时，AMDE明显优于DE算法；求解P5时，AMDE差于DE算法。求解6个实例时，AMDE算法的eb,av和σf均很小，表明其收敛精度高、稳健性好。对于其余4种对比算法，无一算法在求解6个实例时同时具有良好优化性能。由表2 可知，AMDE算法求解实例时的最大函数评价次数为15 000，而CLSDE算法为52 000[6]，因此前者的计算效率更高。综上可知，AMDE算法的性能指标优于4种对比算法。

4 齿轮传动优化设计应用

4.1 齿轮传动优化设计模型

已知某企业使用的二级斜齿圆柱齿轮传动原始数据为：高速轴输入功率P1=8 kW；高速级主动轴转速n1=1450 r/min；传动比itr=9.7，允许传动比误差±5%；动力机为电动机，工作机载荷均匀平稳。大、小齿轮材料为45钢，大齿轮正火处理，硬度185～205 HBS；小齿轮调质处理，硬度为230～255 HBS。许用应力[σH]I=[σH]II= 520 MPa，[σF]I=155 MPa，[σF]II=145 MPa。载荷系数K=1.25。要求以齿轮总体积最小为目标，设计该齿轮传动机构。

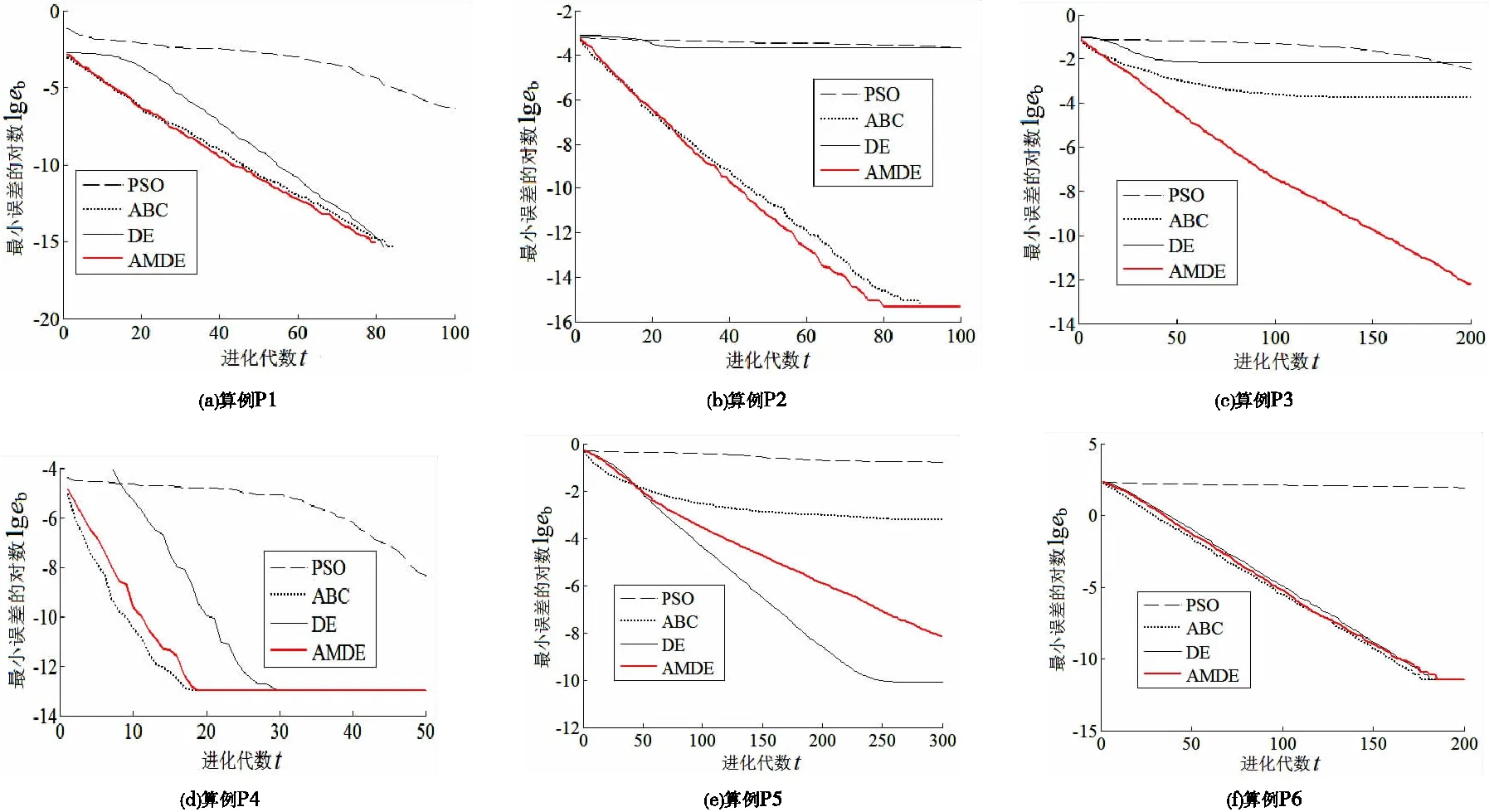
图1 平均最小误差进化曲线

该问题的混合设计变量为：第I级传动，法面模数mnI、小齿轮齿数z1、螺旋角βI、齿宽系数ψdI和传动比iI；第II级传动，法面模数mnII、小齿轮齿数z3、螺旋角βII和齿宽系数ψdII。其中，mnI和mnII为非等间隔离散变量，z1和z3为整数变量；βI、βII、ψdI、ψdII和iI为连续变量。将决策变量记为x=(x1,x2,…,x5)T=(βI,βII,ψdI,ψdII,iI)T，y=(y1,y2,y3,y4)T=(mnI,mnII,z1,z3)T。可根据国家标准，建立模数的离散变量取值列表，再映射为整数变量[12-14]。故，该问题可转化为等效MINLP，再应用第2节的方法求解。

若以齿轮分度圆柱体积近似表示齿轮体积，则总体积最小化设计问题的目标函数为：

minf(x,y)=

式中，z2表示第I级传动大齿轮齿数，取z2=round(x5y3)；z4表示第II级传动大齿轮齿数，取z4=round(itry3y4/z。

参照文献[12]，列出以下约束函数。其中，g1～g4为强度条件，g5为避免第II级大齿轮与第I级传动轴发生干涉的限制条件，g6～g7为最小齿数约束，g8～g9为轴向重合度约束，g10为传动比精度约束，g11～g14为齿宽约束。

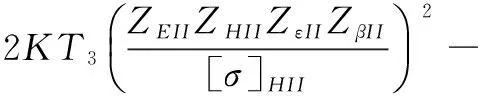
式中，T1,T3为第I,II级传动计算转矩，N·mm，且T1=9.55×106P1/n1，T3=9.55×106x5P1/n1；ZEI,ZEII为第I,II级传动弹性系数；ZHI,ZHII为第I, II级传动节点区域系数；ZεI,ZεII为第I, II级传动重合度系数；ZβI,ZβII为第I, II级传动螺旋角系数；YεI,YεII为第I, II级传动重合度系数；YβI,YβII为第I, II级传动螺旋角系数；YFSI,YFSII为第I, II级传动复合齿形系数。

以上系数的确定方法见文献[15]，其中，将YFSI,YFSII表达为当量齿数的拟合函数。

g5(x,y)=y1z2cosx2+2(y1+50)cosx1cosx2-y2(y4+z4)cosx1≤0

g6(x,y)=17cos3x1-y3≤0

g7(x,y)=17cos3x2-y4≤0

g8(x,y)=π-x3y3tanx1≤0

g9(x,y)=π-x4y4tanx2≤0

g11(x,y)=40-x3y1y3secx1≤0

g12(x,y)=x3y1y3secx1-120≤0

g13(x,y)=40-x4y2y4secx2≤0

g14(x,y)=x4y2y4secx2-120≤0

设计变量的取值范围设置为：0.139 6 rad≤x1,x2≤0.261 8 rad，0.6≤x3,x4≤1.2，2≤x5≤4，y1∈{2, 2.5, 2.75, 3, 3.25, 3.5, 3.75, 4, 4.5, 5} mm，y2∈{3.5, 3.75, 4, 4.5, 5, 5.5, 6} mm，y3,y4∈[15, 30]∩Z。

4.2 优化设计结果

应用AMDE算法求解该设计实例，除取NP=100及tmax=1500外，其余参数设置同第3.2节。算法独立运行10次，最好、最差和平均最优目标函数值分别为2.7623 dm3, 2.7758 dm3和2.7690 dm3，标准差为0.003 949 dm3。该标准差很小，表明算法具有良好稳健性。平均最优值进化曲线如图2 ，由图可知，算法大约进化1200代即收敛于近优解。

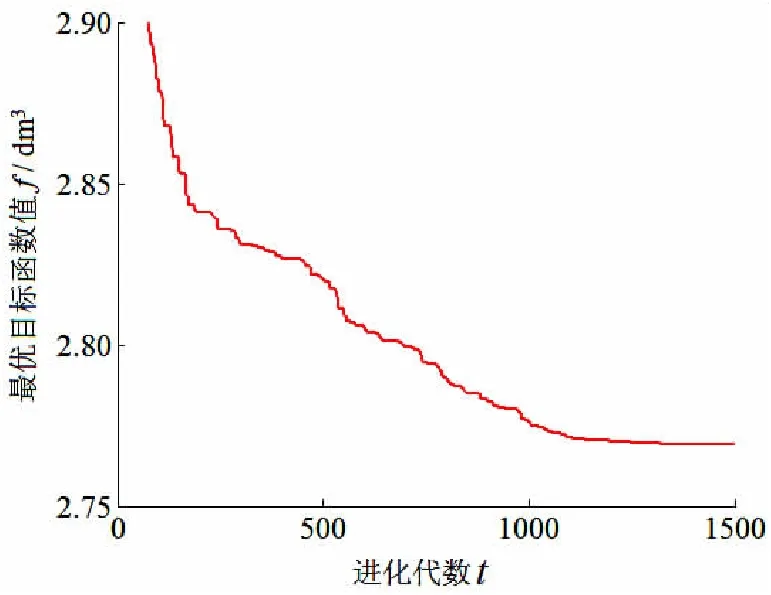
图2 AMDE算法求解案例的平均最优值进化曲线

AMDE算法的最优解见表4 ，将原设计方案也列入表中，以便比较。由表4 可知，应用AMDE算法求得的结果明显优于原设计方案，齿轮体积和较原设计下降约25.5%。

表4 优化设计与原方案结果比较

5 结论

(1)为提高DE算法求解MINLP的优化性能，设计混沌初始化种群、可平衡全局探索与精细开采能力的混合变异版本、基于种群进化停滞代数记录的自适应二次变异算子等新型策略。将诸策略融入DE算法，形成求解MINLP的混合智能算法AMDE。

(2)应用6个MINLP数值实例测试AMDE算法，结果表明：AMDE算法可靠、有效，稳健性优于4种对比算法。

(3)以二级斜齿圆柱齿轮传动体积最小化设计问题，验证AMDE算法求解混合变量工程优化问题的可行性。根据映射关系，将混合离散变量约束优化问题转化为等效MINLP问题，再应用AMDE算法求解该问题。结果显示：AMDE算法可行、有效，具有良好稳健性。与原设计方案相比，AMDE算法的最优解下降了约25.5%。

[1]刘明明,崔春风,童小娇,等.混合整数非线性规划的算法软件及最新进展.中国科学:数学,2016,46(1):1-20.

[2]张甲江,高岳林,高晨阳.非线性混合整数规划问题的改进量子粒子群算法.太原理工大学学报,2015,46(2):196-200.

[3]谭跃,谭冠政,邓曙光.基于遗传交叉和多混沌策略改进的粒子群优化算法.计算机应用研究,2016,33(12):3643-3647.

[4]张莉,李宏,冯大政.求解混合整数规划的嵌入正交杂交的差分进化算法.系统工程与电子技术,2011,33(9):2126-2132.

[5]邓长寿,任红卫,彭虎.混合整数非线性规划问题的改进差分进化算法.计算机应用研究,2012,29(2):445-448.

[6]谭跃,谭冠政,杨冰,等.解决混合整数非线性规划问题的混沌局部搜索差分进化算法.小型微型计算机系统,2012,33(6):1306-1309.

[7]BAI L,WANG J Y,JIANG Y H,et al.Improved hybrid differential evolution-estimation of distribution algorithm with feasibility rules for NLP/MINLP engineering optimization problems.Chinese Journal of Chemical Engineering,2012,20(6):1074-1080.

[8]AKAY B,KARABOGA D.A modified artificial bee colony algorithm for real-parameter optimization.Information Sciences,2012,192:120-142.

[9]GAO W F,LIU S Y,HUANG L L.A global best artificial bee colony algorithm for global optimization.Journal of Computational and Applied Mathematics,2012,236(11):2741-2753.

[10]罗钧,林于晴,刘学明,等.改进蜂群算法及其在圆度误差评定中的应用.机械工程学报,2016,52(16):27-32.

[11]MALLIPEDDI R,SUGANTHAN P N.Ensemble of constraint handling techniques.IEEE Transactions on Evolutionary Computation,2010,14(4):561-579.

[12]车林仙.面向机构分析与设计的差分进化算法研究.徐州:中国矿业大学,2012.

[13]车林仙,程志红.工程约束优化的自适应罚函数混合离散差分进化算法.机械工程学报,2011,47(3):141-151.

[14]车林仙.多样性保持离散差分进化算法及齿轮传动优化应用.机械工程学报,2016,52(21):44-55.

DOI:10.11863/j.suse.2017.01.05

Adaptive Mutation Differential Evolution Algorithm for Mixed Integer Nonlinear Programming

CHELinxian1,2,HEBing2,3a,LIUYongbo3b

(1.School of Mechanical Engineering, Chongqing Vocational Institute of Engineering, Chongqing 402260, China;2.Artificial Intelligence Key Laboratory of Sichuan Province, Zigong 643000, China; 3a.Department of Mechanical Engineering; 3b.Department of Information Engineering, Luzhou Vocational and Technical College,Luzhou 646005, China)

A hybrid differential evolution (DE) algorithm is presented to solve the mixed integer nonlinear programming (MINLP). To enhance the optimization performance of DE algorithm, several new strategies are designed, such as chaotic initializing population, hybrid mutation scheme which can balance global exploration and fine mining abilities, and adaptive second mutation operator based on the recording generations of evolutionary stagnation for a population. The aforementioned strategies are embedded in DE algorithm and an adaptive mutation DE (AMDE) algorithm is formed for solving MINLP. Six numerical examples of MINLP are tested comparatively to show that this new approach is valid and reliable. Finally the proposed AMDE algorithm is used to solve a real case of engineering optimization for minimizing volumes of gear transmission, so the practical applicability of the new algorithm is indicated.

mixed integer nonlinear programming; differential evolution algorithm; artificial bee colony algorithm; adaptive mutation operator; optimal design of gear transmission

2016-10-24

重庆市基础科学与前沿技术研究专项资助项目(cstc2015jcyjA70006);重庆市教育委员会科学技术研究项目(KJ1403201);人工智能四川省重点实验室开放基金项目(2013RYJ02)

车林仙(1971-),男,四川泸州人,教授,博士,主要从事机械优化设计、机构学及智能信息处理方面的研究,(E-mail)lx.che@163.com

1673-1549(2017)01-0019-08

10.11863/j.suse.2017.01.04

TP18;O221.4

A