黄龙体育中心动力弹塑性时程分析

肖本林， 王 雪， 金绍武， 邵兴宇

(1 湖北工业大学土木工程与建筑学院，湖北 武汉 430068; 2 中南建筑设计研究院股份有限公司，湖北 武汉 430068)

黄龙体育中心动力弹塑性时程分析

肖本林1， 王 雪1， 金绍武1， 邵兴宇2

(1 湖北工业大学土木工程与建筑学院，湖北 武汉 430068; 2 中南建筑设计研究院股份有限公司，湖北 武汉 430068)

以黄龙体育中心为例探讨抗震设计对结构稳定性的作用。工程采用框架-剪力墙结构，局部采用跨层预应力混凝土桁架结构，屋盖采用空间钢网格结构。运用现行结构抗震理论和有限元分析，对该结构进行了动力时程和静力弹塑性分析。分析表明：该结构整体抗侧刚度较好，具有较好的抗震性能。

钢筋混凝土结构；结构抗震;有限元分析；时程分析；静力弹塑性分析

1 工程背景

浙江省黄龙体育中心游泳跳水馆位于杭州市区内黄龙体育中心4号地块，总建筑面积约为48 878 m2。工程分为地上四层和地下三层，局部设夹层。根据《建筑工程抗震设防分类标准》GB50223-2008 6.0.3条及本条条文说明，观众席座位数为3000，小于4500，抗震设防类别为标准设防类。建筑最高点标高29.70 m,上部建筑最大平面尺寸为128 m×74.3 m，采用框架-剪力墙结构，局部采用跨层预应力混凝土桁架结构，屋盖采用空间钢网格结构。地下室长114.3 m，宽88.4 m。地下一层层高为5.0 m，地下二、三层层高均为4.2 m。地下室第三层考虑人防设计，人防等级为常6级和核6级。基本轴网尺寸为8.4 m×8.4 m。地下室不设缝，为一个整体。

2 分析模型

2.1 分析方法

静力弹塑性分析方法(如Pushover[1]分析方法)适用范围：适用以第1振型破坏为主的结构；适用接近无限刚和分块无限刚的结构。

根据弹性分析结果，上部结构不满足上述适用条件，静力弹塑性分析的方法不适用于本工程，因此，采用动力弹塑性时程分析方法。直接模拟结构在地震力作用下的非线性反应，该方法未作任何理论的简化，是目前结构非线性地震反应分析领域最完善的方法。考虑以下因素：

几何非线性：结构的动力平衡方程建立在结构变形后的几何状态上，大变形效应等都被精确考虑;材料非线性：直接在材料应力-应变本构关系的水平上模拟;动力方程积分方法：直接积分，可以准确模拟结构的破坏形态。[2]

2.2 模型数据来源

对该复杂建筑结构进行动力弹塑性时程分析，能否较为准确地考虑配筋对构件承载力和刚度的贡献是分析正确与否的前提条件。本工程配筋数据采用SAP2000的初步设计数据，并按照中、大震等效弹性分析的配筋结果。SAP2000整体模型见图1。

图 1 SAP2000整体模型

3 分析条件

3.1 地震波选用

根据《建筑抗震设计规范》(GB50011-2010)规定，选用在弹性时程分析中结构反应较大的两条天然波El Centro波和LEXINGT波，以及一条人工波，三条波的时程曲线见图2～图4。

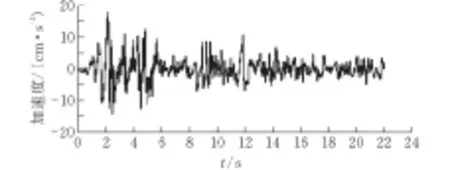
图 2 EL Centro地震波

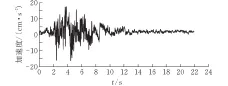
图 3 LEXINGT地震波

图 4 人工波

地震波间隔时间/s持续时间/s规范峰值/(cm﹒s-2)ElCentro0．0220125LEXINGT0．0220125人工波0．0220125

说明：规范峰值为规范规定的6度罕遇地震时程分析所用地震加速度时程的最大值。

在进行分析时，通过定义比例系数，将地震波的峰值放大到规范要求。

3.2 分析工况

根据《建筑抗震设计规范》GB50011-2010 10.2.11条规定，对于一般的大跨屋盖结构，应进行三向地震作用分析。再依据抗震规范5.1.2条条文解释，三向地震同时输入时，其地震动参数(加速度峰值或反应谱最大值)比例取：水平主向∶水平次向∶竖向 = 1∶0.85∶0.65。故分析过程中定义两个地震工况。当X向为主方向时，加速度峰值比例为X∶Y∶Z = 1∶ 0.85 ∶ 0.65(以下简称为XY工况)。当Y向为主方向时，加速度峰值比例为Y∶X∶Z = 1∶ 0.85∶ 0.65(以下简称为YX工况)。

分析过程中，首先进行施工模拟加载，形成施工结束后的刚度，然后施加非线性的附加恒载和活载工况。分析完成后，以此时的刚度为起点，进行非线性动力时程分析[3]。

4 分析结果

4.1 指标对比

基底剪力及层间位移角计算结果与小震反应谱计算及弹性时程分析计算结果的对比见表2。其中，表中所列的层间位移角为最大的层间位移角，最大位移角位于6 m标高处。

由表3中数据可以看到，输入不同的地震波，计算的结果有一定的离散性。

1)中震作用下结构的基底剪力均值约是规范小震作用下结构的基底剪力均值的3倍左右。

2)大震作用下结构的基底剪力均值约是规范小震作用下结构的基底剪力均值的6～8倍。

4.2 基底剪力

提取三条地震波作用下的基底剪力曲线，最大值及最小值见表4。

续表1

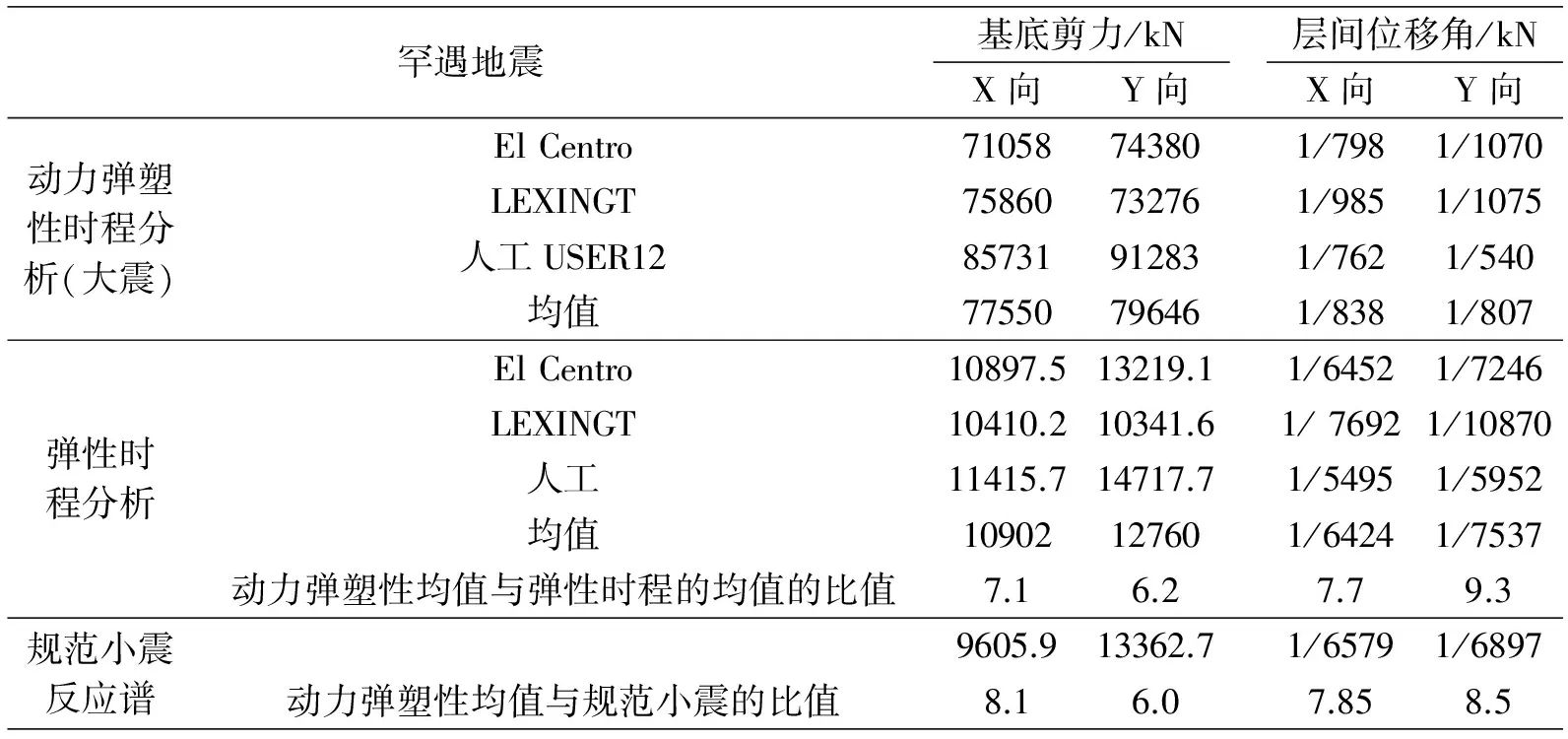
罕遇地震基底剪力/kNX向Y向层间位移角/kNX向Y向动力弹塑性时程分析(大震)ElCentro71058743801/7981/1070LEXINGT75860732761/9851/1075人工USER1285731912831/7621/540均值77550796461/8381/807弹性时程分析ElCentro10897．513219．11/64521/7246LEXINGT10410．210341．61/76921/10870人工11415．714717．71/54951/5952均值10902127601/64241/7537动力弹塑性均值与弹性时程的均值的比值7．16．27．79．3规范小震反应谱9605．913362．71/65791/6897动力弹塑性均值与规范小震的比值8．16．07．858．5

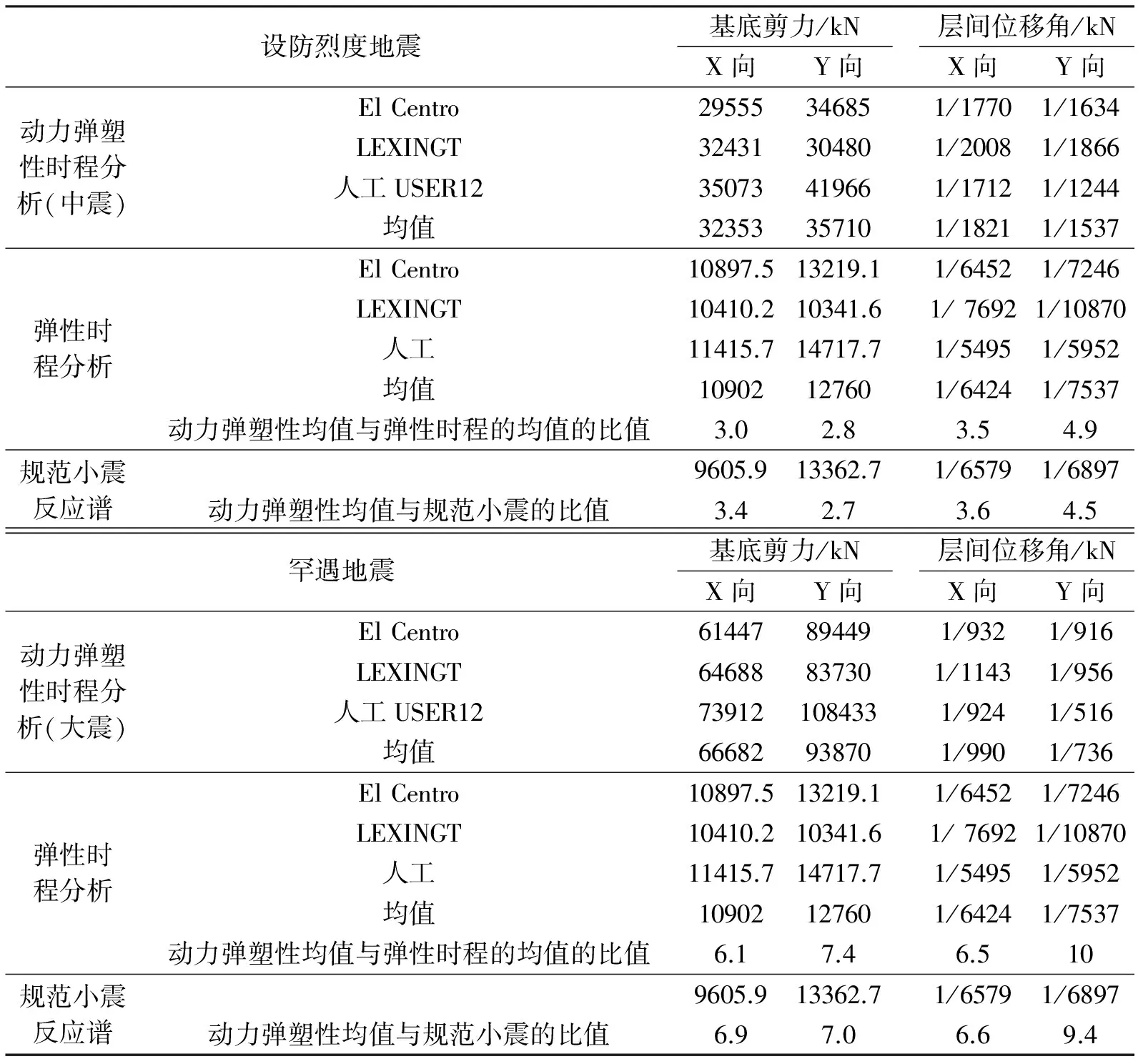
表3 荷载工况2：三向地震作用，Y∶X∶Z = 1∶:0.85∶0.65

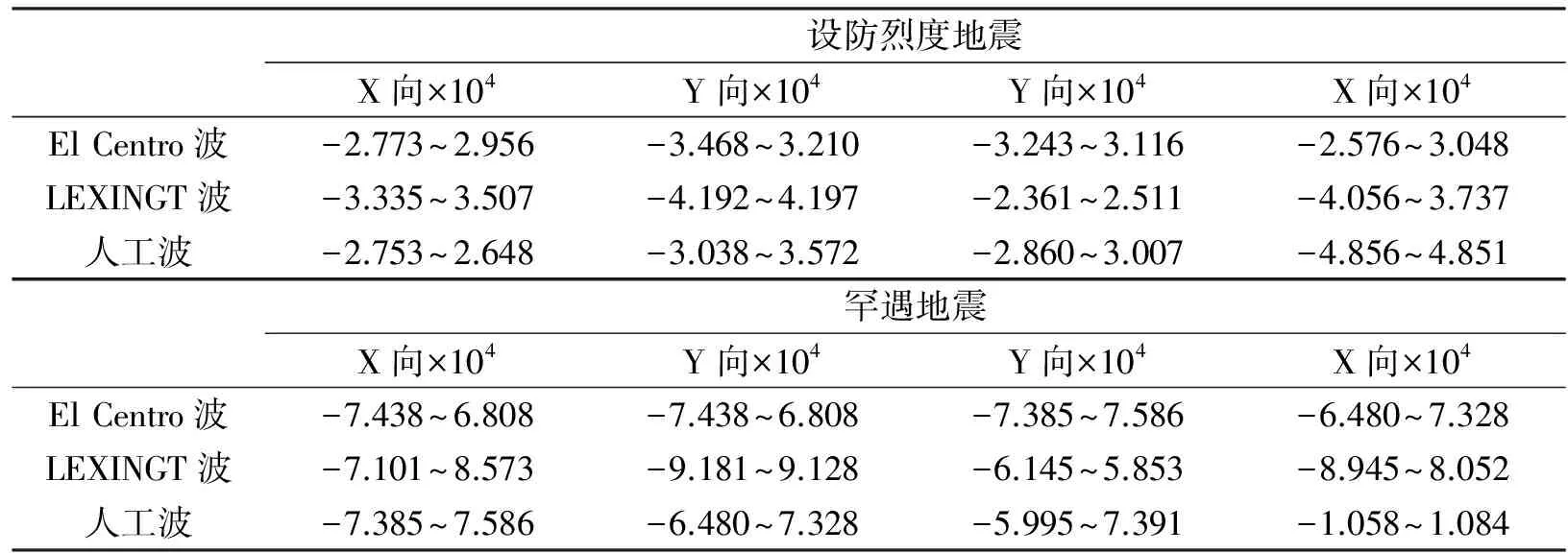
表4 各波形基底剪力值

4.2 层间位移角计算结果

计算层间位移角时，选取结构中的柱子，分别查看它们的层间位移角，然后选取各层最大的层间位移角，得到层间位移角表格。 各层最大层间位移角见表5～表7。

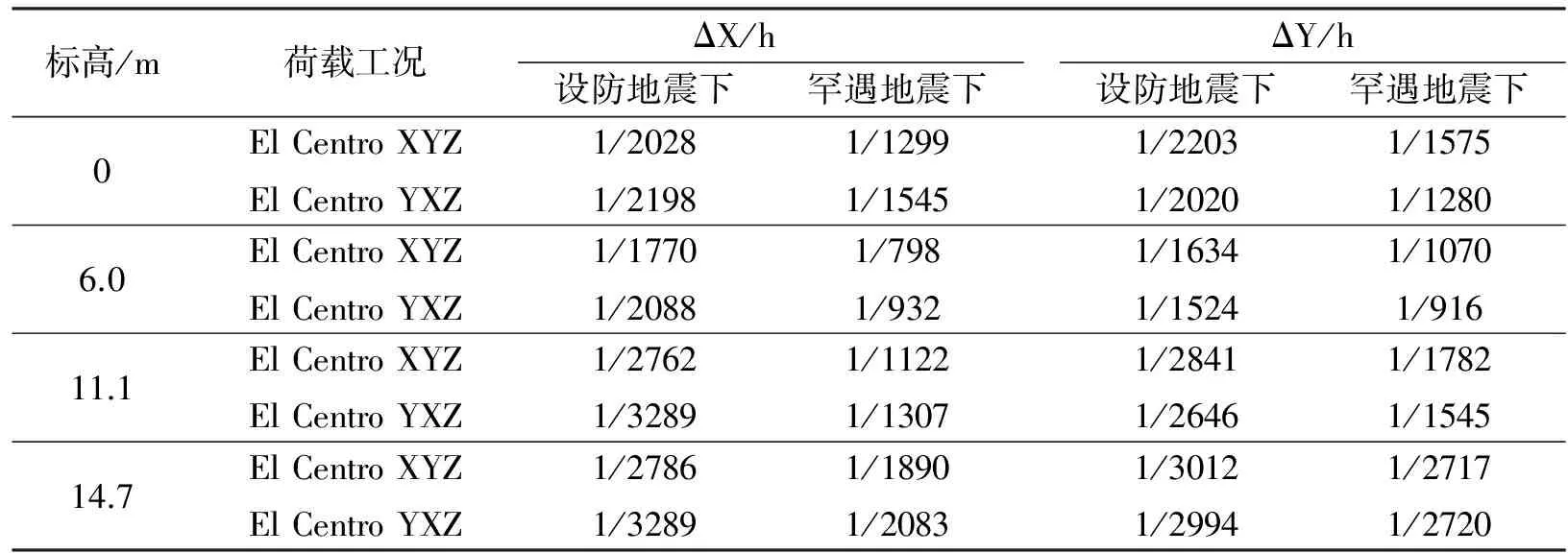
表5 El Centro波的层间位移角

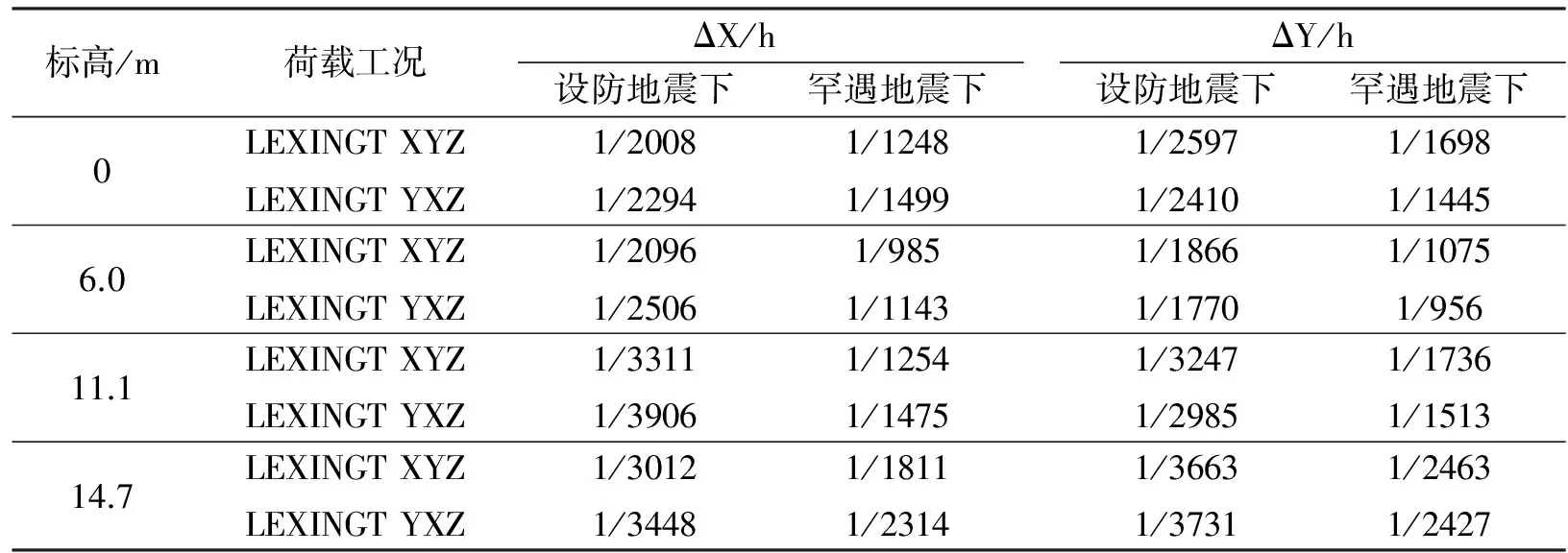
表6 的层间位移角

表7 人工波的层间位移角

5 性能评估

5.1 设防地震作用

1)整体模型出铰图见图5，右侧为塑性铰变形图例。

图 5 设防地震整体模型出铰图

从计算结果可以看出，结构整体出铰数量极少。大悬挑部位都保持在弹性状态，塑性铰出现在框架梁上。从塑性铰的变形程度来看，都位于B～IO阶段。

2)选择关键构件查看塑性铰结果，见图6。

图 6 设防地震塑性铰变形图例

由图6可见框架柱和大悬挑部位的构件都保持在弹性状态。

5.2罕遇地震作用

1)整体模型出铰图见图7，右侧为塑性铰变形图例。从计算结果可以看出，结构整体出铰数量不多，大部分集中在大悬挑的部位，其余少数分布在框架梁和框架柱上。从塑性铰的变形程度看，大部分塑性铰都位于B～IO之间，还有一定的变形储备。

图 7 罕遇地震整体模型出铰图

2)选择关键构件查看塑性铰结果(图8)。大悬挑部位塑性铰出现较多。取从左至右的四榀桁架进行放大观察(图9)。

图 8 罕遇地震塑性铰变形图例

从图中可以看出，悬挑部位部分梁、柱、腹杆均出现塑性铰，进入非线性阶段。绝大多数塑性铰的变形都位于B～IO阶段，变形较小，符合性能目标要求，有一定的安全储备。设计时需采取一定的措施进行加强。[4]

6 结论

1)结构在设防地震作用下的弹塑性层间位移角满足规范限值。结构在设防地震作用下，大部分框架梁保持弹性，少量框架梁出现塑性铰，塑性变形较小，位于B～IO之间。框架柱和大悬挑部位全部保持弹性，满足性能要求。总体来说，结构满足既定性能目标。

2)结构在罕遇地震作用下的弹塑性层间位移角满足规范限值。结构在罕遇地震作用下，大部分框架梁、框架柱保持弹性，少量框架梁、框架柱出现塑性铰，塑性变形较小，位于B～IO之间。大悬挑部位出现较多塑性铰，但都变形很小，处于IO阶段，满足性能要求。总体来说，结构满足既定的抗震性能目标。

[1] 胡聿贤,地震工程学[M].第2版.北京：地震出版社, 2006:93-104.

[2] 方鄂华，高层建筑钢筋混凝土结构概念设计[M].北京：机械工业出版社，2004

[3] GB 50011 —2001建筑抗震设计规范[S].北京：中国建筑工业出版社,2001.

[4] 叶列平，马千里，缪志伟.结构抗震分析用地震动强度指标的研究[J].地震工程与工程振动，2009, 29(4)：9-22.

[责任编校： 张岩芳]

Elastic-plastic Time-history Analysis on the Dragon Sports Centre

XIAO Benlin1, WANG Xue1, JIN Shaowu1, SHAO Xingyu2

(1SchoolofCivilEngin.,ArchitectureandEnvironment,HubeiUniv.ofTech.，Wuhan430068，China; 2Central-SouthArchitecturalDesignInstituteCo.Ltd.Wuhan430068，China)

The paper takes the Dragon Sports Centre as an example to discuss the effect of seismic design on the stability of the structure . Frame - shear wall structure was applied in the project, cross layer restressed concrete truss structure applied in partial structure, and space steel grid structure applied in the roof. It used the existing structure seismic theory and finite element analysis to make dynamic and static elastoplastic analysis on the structure. Analysis shows that the structure is in a good lateral stiffness, and has better seismic performance.

reinforced concrete structure; structural seismic; The finite element analysis; time history analysis; static elastoplastic analysis

2016-01-26

肖本林(1962-)， 男， 湖南安乡人, 工学博士,湖北工业大学教授，研究方向为土木工程与建筑学

王 雪(1990-)， 男，湖北荆州人，湖北工业大学硕士研究生，研究方向为工程力学

1003-4684(2017)01-0014-05

TU352

A