基于区间联系隶属度的土体胀缩性评价模型

朱 宇, 汪明武, 李亚峰, 蒋 辉

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

基于区间联系隶属度的土体胀缩性评价模型

朱 宇, 汪明武, 李亚峰, 蒋 辉

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章基于区间联系隶属度概念描述实测指标与标准等级间的同、异、反关系,进而构建膨胀土和改良土胀缩性评价新模型,并通过二元联系集对势表达待评样本的胀缩性等级,以克服区间数难以比较的缺陷。实例应用及与其他方法对比分析表明,该模型应用于膨胀土和改良土胀缩性评价是有效可行的,评价结果能充分反映实际数据区间波动特点。

膨胀土;胀缩性;区间数;联系隶属度;集对势

膨胀土具有往返可逆的吸水膨胀和失水收缩特性,影响到地基处理工程的设计和安全[1-2],故工程界常用掺石灰方法来治理膨胀土,但若施工不注意改良土的收缩性和施工质量控制,也可能导致工程灾难,造成巨大的经济损失,因此,膨胀土和石灰改良膨胀土的胀缩等级合理评定具有重要的工程应用价值。然而,胀缩性评价问题涉及诸多具有区间分布特点的不确定性因素,是一个极其复杂的问题。国内外研究者对此问题开展了诸多研究[3-10],提出了基于模糊数学和灰色理论[3-4]、神经网络[5]和可拓论[6]、粗糙集[7]、集对分析理论[8-9]和云模型理论[10]等评价方法,但这些方法难以描述膨胀土和改良土胀缩性评价指标的区间特性,加上评价指标获取信息的不完整性和局限性以及人类思维的模糊性,致使该问题仍未得到很好解决。本文探讨以区间数形式直接描述膨胀土和改良土胀缩性评价问题,并引入集对理论分析其内在确定和不确定的信息,实现统一反映指标的动态不确定性特点,以提高胀缩性评价结果的可靠性。

1 区间联系隶属度评价模型

1.1 基本原理

首先基于区间数表达待选样本的评价指标体系和分类标准集构成集对,以分析同异反关系,计算相应的区间联系隶属度,并构建评价矩阵;然后结合评价指标权重集成区间联系隶属度,并基于二元联系数集对势表达区间联系隶属度及最大区间隶属度原则确定样本等级。

1.2 评价流程

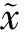
(1)

其中,x-为区间数的下界;x+为区间数的上界。

(2) 基于集对同异反关系分析,计算指标区间联系隶属度,并构建评价矩阵。若将胀缩性某个评价指标的等级划分为K等级,则样本实测值与讨论等级k的同一、差异和对立关系如图1所示[12]。当x处于讨论区间k内时,集对关系为同一;当x处于相隔区间时,集对关系为对立;当x处于相邻区间时,两者为差异关系。在此应用集对联系隶属度表达确定和不确定统一关系。联系隶属度是在传统联系度的基础上拓展的概念,其满足质与量互变定理和对立统一原理,更能满足实际工程不确定性问题的应用分析，其计算公式为(2)式。

图1 点与区间集对同异反关系示意图

(2)

其中,μij为联系隶属度,μij∈[-1, 1];x为指标值区间数的上界或下界;Mk-1、Mk、Mk+1、Mk+2为划分区间的界限值。

(3) 结合样本指标权重计算集成联系隶属度。通过对各指标区间数联系隶属度的分析,代入(2)式求出各指标隶属区间评估等级向量后,集成得到多个指标的隶属区间评估等级矩阵R，即

(3)

当确定了评价指标的权重向量ω=(ω1ω2…ωm),∑ωi=1,则样本关于某一评价等级的集成联系隶属度bj为:

(4)

则相应的评价结果向量B为：

(5)

(4) 等级确定。对获得的区间集成联系隶属度进行比较,最大区间数对应的等级即为相应的样本胀缩性等级。

1.3 区间数的二元联系数表达

集对势大小可判别系统的倾向性状态,具有化繁为简和便于不确定性分析的优点,因此基于联系数态势表达区间数,可将区间数大小的比较转换为比较二元联系数的同异势大小,从而实现区间数直接排序。对于胀缩性评价问题,基于区间联系隶属度评价模型的计算结果可表达为二元联系数μ=a+bi形式,其中i∈[-1, 1]。评价结果区间数中大于0的部分可代表同一关系,该部分区间长度与总区间长度的比即为a；大于-1小于0的部分代表差异关系,该部分区间长度与总区间长度的比即为b,因此可应用二元联系数的同异势[11]进行倾向性分析,计算模型为:

(6)

2 实例应用

现以合肥新桥机场膨胀土工程资料为例开展膨胀土和改良土的胀缩性评价,并与其他分析方法的结果对比分析,以验证本文评价模型的可行性和可靠性。选用液限、胀缩总率、塑性指数、天然含水率和自由胀缩率5个评价指标,胀缩性等级划分为极高(Ⅰ)、高(Ⅱ)、中(Ⅲ)和低(Ⅳ)4个等级,基于区间数表达的胀缩性等级评价标准和实测指标值见表1、表2所列。

表1 膨胀土和改良土胀缩性等级评价指标标准的区间数表达

表2 区间数表达的样本值

现以原状土为例说明评价模型的计算过程。当计算单项指标“液限”关于等级Ⅱ的联系隶属度时,将实测数据带入(2)式,经计算可得联系隶属度μ12=[-0.46,-0.36]。同理可得其他评价指标关于各等级的联系隶属度μij,则可构建联系隶属度评价矩阵R，即

为便于对比分析,评价指标权重直接采用文献[13]中的权重,ω=(0.23 0.22 0.20 0.19 0.16),∑ωi=1,再代入(4)式和(5)式可计算得到原状土对各等级的联系隶属度为:

B=([-1.000,-0.913][-0.554,-0.218]

由计算结果可知,该土样与等级Ⅲ的同一度最大,因此评定该土样的胀缩性等级为Ⅲ级。按照以上计算过程,同理可得其他待评样本对各等级的集成联系隶属度,实例评价结果及与云模型方法[10]、集对分析法[14]和功效系数法[15]的结果对比见表3所列。

由表3可知,7%灰土(现场)样本对各等级的集成联系隶属度为：

B=([-0.962,-0.785][-0.823,-0.248]

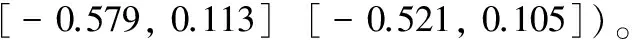
对于区间数[-0.579, 0.113]、[-0.521, 0.105]的大小判断,应将其转为二元联系数,然后再做判断。通过联系隶属度概念知,区间数中大于0的部分代表同一关系,在(-1,0]区间代表差异关系,可将该区间数转为二元联系数，即μ3=0.164+0.836i,μ4=0.167+0.833i,代入(6)式，则它们的趋同势分别为Shi(U)a3=0.196,Shi(U)a4=0.201,由于后一区间数的趋同势更大,所以评定该土样的胀缩性等级为Ⅳ级。

由表3结果可知,基于区间数联系隶属度的评价结果与云模型方法、集对分析方法和功效系数方法所得结果完全吻合,表明了本文方法应用于膨胀土和改良土胀缩性等级评价是有效可行的,且本文模型直接采用区间数描述问题,避免了以往采用确切数不能充分反映实际数据波动区间的弊端,使评价结果更具有代表性,而且基于集对势分析区间数大小,克服了传统区间数比较大小难题,可使结果更为直观和合理,便于工程应用。

表3 实例评价结果及对比

3 结 论

膨胀土和改良土胀缩性判别和等级评价受诸多不确定性因素的影响,且实际评价指标具有区间数的特点。本文探讨了基于区间联系隶属度的膨胀土和改良土胀缩性评价模型,解决了以往应用确切数代替区间数分析的弊端,并能通过二元联系数表达结果,克服了以往区间数比较分析过程繁琐的缺陷。实例应用结果表明,将该方法应用于膨胀土和改良土胀缩性等级分析评价是有效可行的。本文方法可为其他类似评价问题提供参考。

[1] 唐朝生,施斌.干湿循环过程中膨胀土的胀缩变形特征[J].岩土工程学报,2011,33(9):1376-1384.

[2] 查甫生,崔可锐,刘松玉,等.膨胀土的循环胀缩特性试验研究[J].合肥工业大学学报(自然科学版),2009,32(3):399-402.

[3] 罗文柯,杨果林.模糊数学对湖南膨胀土分类与判别实际工程应用研究[J].南华大学学报(自然科学版),2006,20(2):12-16.

[4] 李玉花,冯晓腊,严应征.灰色聚类法在膨胀土分类中的应用[J].岩土力学,2003,24(2):304-306.

[5] 吕海波,赵艳林,孔令伟,等.自适应模糊神经网络在膨胀土胀缩等级分类中的应用[J].岩土力学,2006,27(6):908-912.

[6] 汪明武,金菊良,李丽.可拓学在膨胀土胀缩等级评判中的应用[J].岩土工程学报,2003,25(6):754-757.

[7] 丁加明,王永和,丁力行.基于粗糙集的膨胀土分级指标重要性分析[J].岩土力学,2006,27(9):1514-1518.

[8]WANGMingwu,CHENGuangyi.Anovelcouplingmodelforriskanalysisofswellandshrinkageofexpansivesoils[J].ComputersandMathematicswithApplications,2011,62(7):2854-2861.

[9] 汪明武,赵奎元,张立彪.基于联系期望的膨胀土和改良土胀缩性评价模型[J].岩土工程学报,2014,36(8):1553-1557.

[10] 汪明武,李健,徐鹏,等.膨胀土与石灰改良膨胀土胀缩性的云模型评价[J].东南大学学报(自然科学版),2014,44(2):396-400.

[11] 刘秀梅,赵克勤.区间数决策集对分析[M].北京:科学出版社,2014:10-52.

[12] 汪明武,金菊良,周玉良.集对分析耦合方法与应用[M].北京:科学出版社,2014:21-22.

[13] 蔡奕,王宝军,施斌,等.GIS环境下膨胀土胀缩等级的模糊数学评判[J].工程勘察,2002(2):1-4.

[14] WANG Mingwu,QIN Shuai,HUA Peng.Risk analysis of shrink and expansion for expansive soils and improved expansive soils in the Xinqiao airport runway of Hefei[J].Applied Mechanics and Materials,2011,90/91/92/93:1307-1312.

[15] 李健,徐鹏,秦帅,等.膨胀土与改良土胀缩性等级评价[J].合肥工业大学学报(自然科学版),2013,36(8):969-973.

(责任编辑 张淑艳)

A novel evaluation model of swelling-shrinkage grade of soil mass based on interval connectional membership degree

ZHU Yu, WANG Mingwu, LI Yafeng, JIANG Hui

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

A novel evaluation model of swelling-shrinkage grade for untreated and treated expansive clays using the interval connectional membership degree is presented to depict the identical-discrepancy-contrary relationships between the indexes of measured samples and classification standards of swelling-shrinkage grade. And the swelling-shrinkage grade is further expressed as the set pair potential of two-element connection number to overcome the defect that the interval number is difficult to compare. The results of case study and comparison with other methods show that the proposed model is effective and feasible, and the evaluation results can fully reflect the fluctuation characteristics of actual data.

expansive clay; swelling-shrinkage; interval number; connectional membership degree; set pair potential

2015-09-09

国家自然科学基金资助项目(41172274)

朱 宇(1992-),男,安徽合肥人,合肥工业大学硕士生; 汪明武(1972-),男,安徽歙县人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.01.013

TU443

A

1003-5060(2017)01-0067-04