有限时段源一维水质模型的求解及其简化条件

武周虎

（青岛理工大学 环境与市政工程学院，山东 青岛 266033）

在《建设项目环境风险评价技术导则》［1］中指出：有毒有害物质进入水环境的途径包括事故直接导致和事故处理处置过程间接导致，污染物进入水体的方式一般包括“瞬时源”和“有限时段源”。但在该导则中并未给出有限时段源一维水质模型的求解，对后者若排放数小时仍按瞬时源模型来处理，会给环境风险防范与应急工作带来不利影响。在以往的教科书［2-3］和文献报道［4-6］中，仅给出了瞬时源模型的解析解、稳态源模型的解析解和连续源模型浓度分布的积分形式。武周虎等［7-8］在间隙性排放源条件下，给出了一维移流离散水质模型的解析解，适用于周期性间隙排放情况下沿程污染物浓度分布的计算；彭应登等［9］给出的有限时段源（连续源）浓度积分公式被积函数中变量t未改为一系列瞬时源到计算时间的扩散历时（t-τ），错误的对变量t求积分，因此，无法据此获得正确结果。

本文在等强度有限时段源条件下，从一维移流离散水质模型方程出发，采用变量替换和拉普拉斯变换的数学方法，求解河流污染物浓度分布的解析解，进行不同扩散历时“有限时段源”与“瞬时源”沿程污染物浓度分布的比较分析，给出有限时段源可以按瞬时源计算的简化判别条件，为建设项目水环境风险影响预测与评价以及增强《环境风险防范措施和环境风险应急预案》的可靠性，提供理论支持。

1 有限时段源的模型方程与求解条件

根据武周虎［10］提出的基于环境扩散条件的河流宽度分类判别准则，对于窄小河流，如果河道顺直且可以概化为恒定均匀流，污水排入河流后很快在较短的时间（距离）内达到全断面均匀混合，河流中有毒有害物质的断面平均浓度可按一维纵向移流离散问题处理。

如果污染物的排放不是一次性瞬时完成，而是排放持续一段时间t0后完全停止，把这种污染源称为“有限时段源”。将排污口断面设为坐标原点O，沿河流流向的纵向坐标为x。设初始时间t=0在 x轴上的有毒有害物质浓度为零，背景浓度暂不计入。当时间0＜t≤t0时，在x=0处排放有毒有害物质的全断面均匀混合浓度C0维持不变，当时间t＞t0时，在x=0处的排污停止，污染物浓度维持为零。采用一维移流离散水质模型方程［2］：

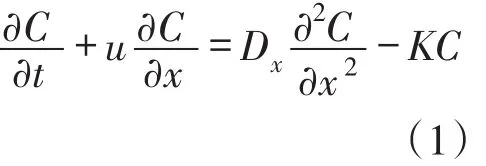
式中：C为污染物的浓度，单位为mg/L；u为平均流速；Dx为纵向离散系数；K为污染物的降解速率系数；t为从开始排放计算的扩散历时（时间）。除浓度外，其它变量和参数均采用m-s单位制。

求解条件为：C|t=0，对一切x=0，C|0＜t≤t0，x=0=C0，C|t＞t0，x=0=0，C|t＞0，x=±L=0，其中L足够大。

2 有限时段源模型方程的求解过程

2.1模型方程的变形处理首先，进行第一次变量替换，令给变换式两边分别对t和x求一阶偏导数，再对x求二阶偏导数，代入式（1）整理得到：

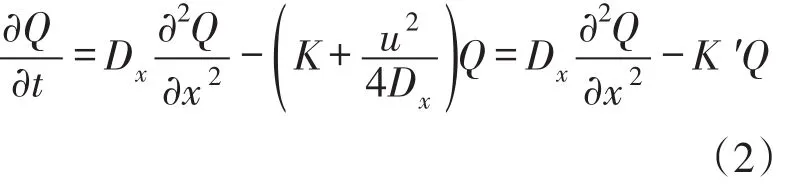
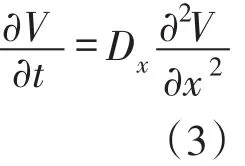
2.2拉普拉斯变换及求解对式（3）关于t取拉普拉斯变换，0≤t＜∞。在t=0和t=t0处均属于第一类间断点，满足拉普拉斯变换的存在条件［11］，将原函数和一阶偏导数的拉普拉斯变换分别记为：

将式（4）和式（5）代入式（3）得到：

将初始条件V|t=0，对一切x=0代入式（6），则有：

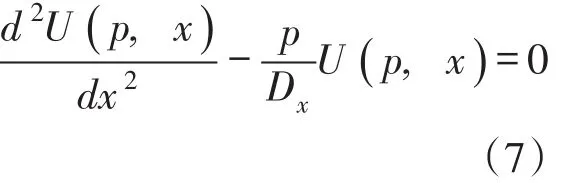
边界条件相应变为：当0＜t≤t0时当t＞t0时，U（p，0）=0；当t＞0时，U（p，±L）=0。 不难得到，二阶线性齐次微分方程式（7）的通解为：

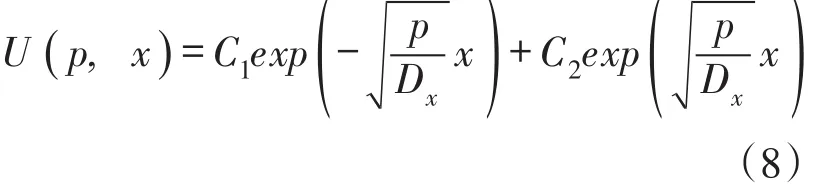
式中：C1、C2为积分常数。

根据给定边界条件，可得出方程式（8）中的积分常数C1和C2。对于排污口断面的下游河段x≥0有：当0＜t≤t0时，由得到由U（p，+L）=0得到C2=0；当t＞t0时，由U（p，0+）=0得到C1=0，由U（p，+L）=0得到C2=0。则有：

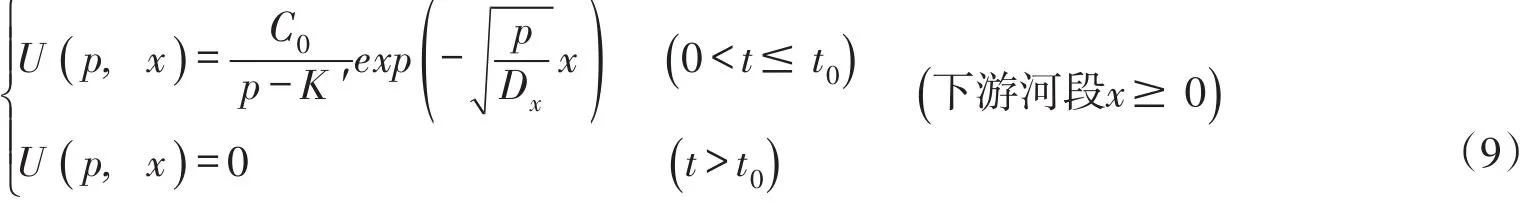
对于排污口断面的上游河段x＜0有：当0＜t≤t0时，由得 到 C2=由U（p，-L）=0得到C1=0；当t＞t0时，由U（p，0-）=0得到C2=0，由U（p，-L）=0得到C1=0。则有：

2.3拉普拉斯逆变换对式（9）和式（10）分别取拉普拉斯逆变换得到：

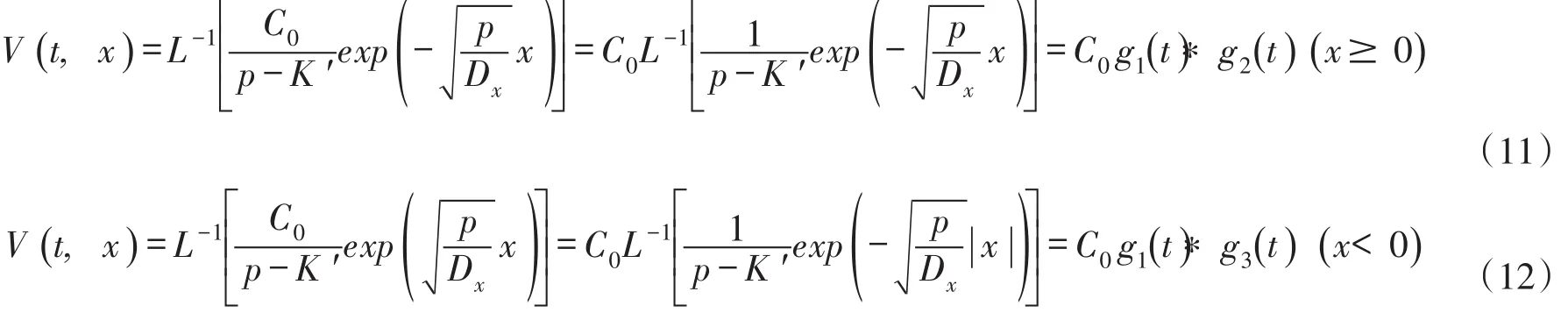
式中：g1（t）*g2（t）称为函数g1（t）和g2（t）的卷积积分；g1（t）*g3（t）称为函数g1（t）和g3（t）的卷积积分。

由拉普拉斯逆变换表查知［11］：

对下游河段x≥0，将g1（t）和g2（t）代入式（11），并应用卷积积分得到：

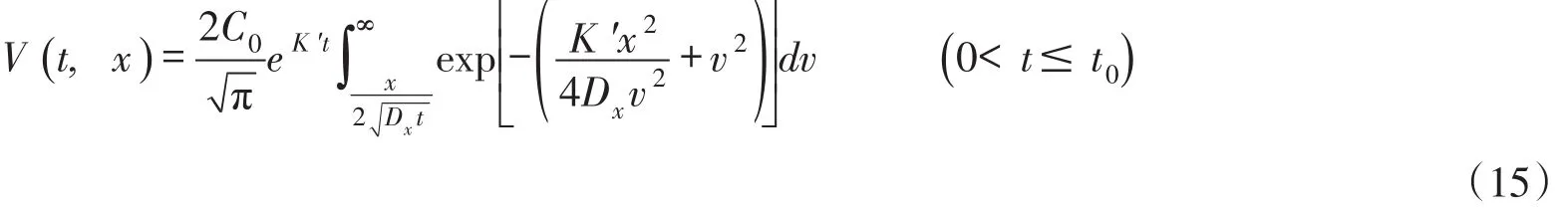
同理，式（14）变为：

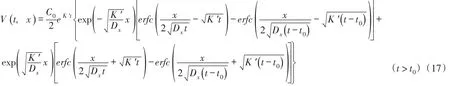
对上游河段x＜0，将g1（t）和g3（t）代入式（12），并应用卷积积分得到：

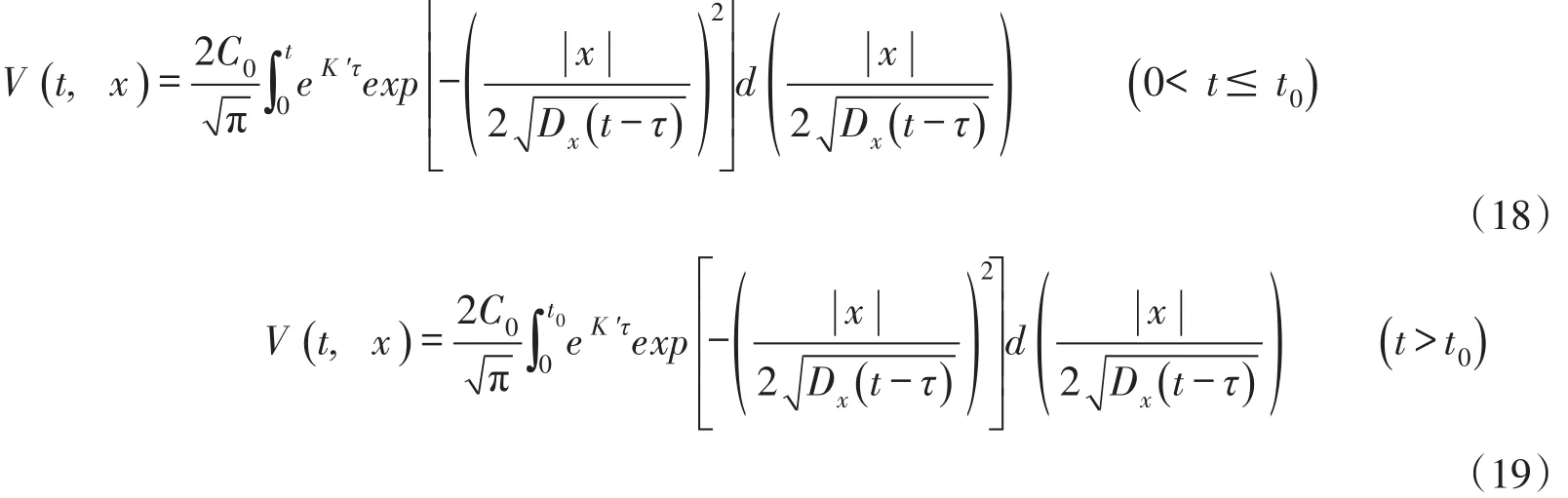
采用上述式（13）—（17）类似的求解过程得到：

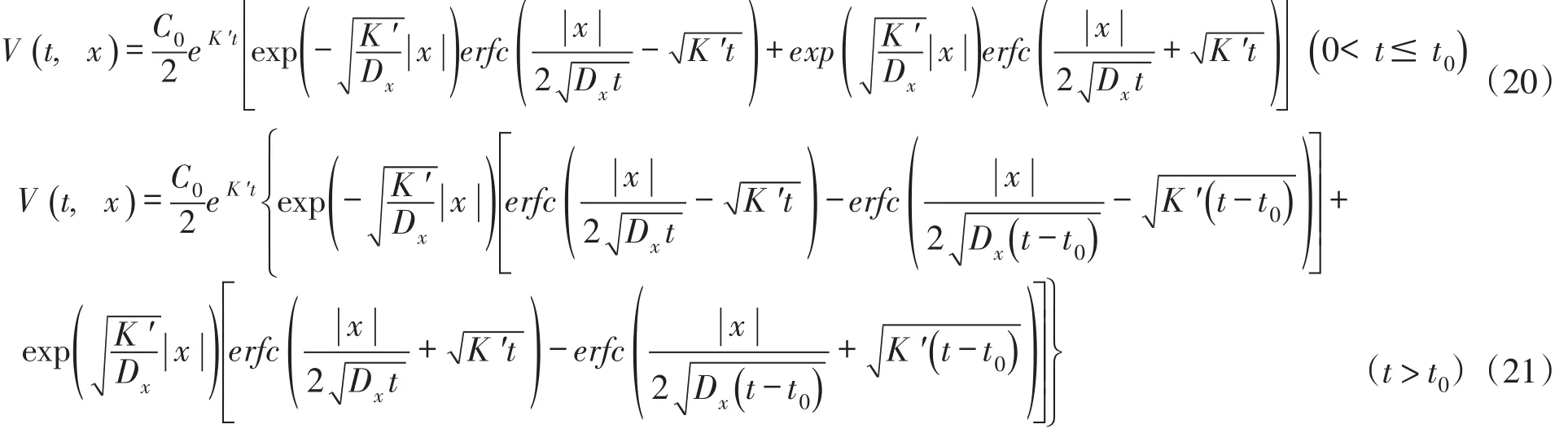
2.4浓度分布公式按照2.1节中两次变量替换的逆序，对函数V（t，x）进行还原计算。在有限时段源排放持续期间（0＜t≤t0），由式（16）和式（20）分别还原化简得到：

下游河段x≥0：

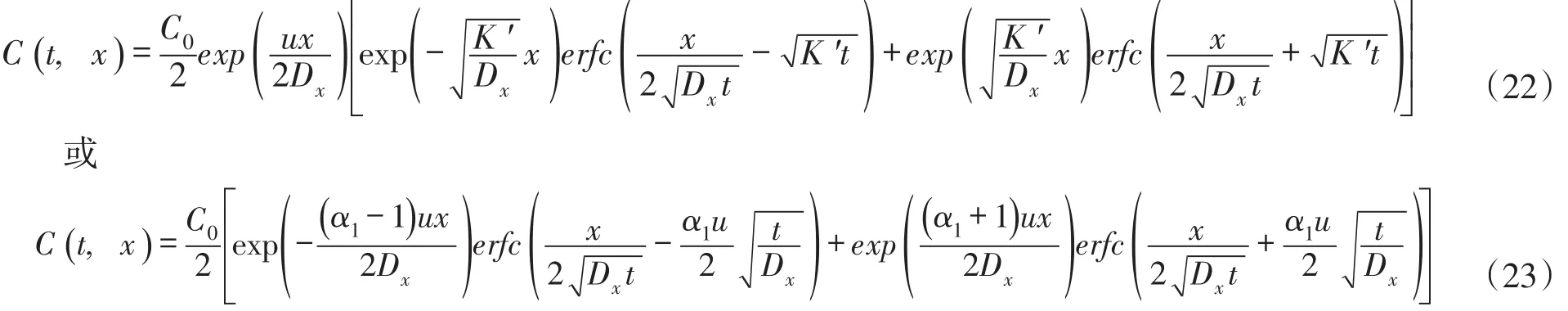
上游河段x＜0：

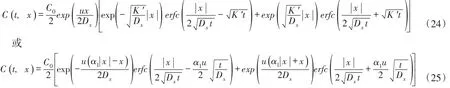
式（22）—（25）就是在有限时段源排放持续期间（0＜t≤t0），排污口断面下游和上游河段一维水质模型方程污染物浓度分布的解析解。

在有限时段源排放停止后（t＞t0），由式（17）和式（21）分别还原化简得到：

下游河段x≥0：

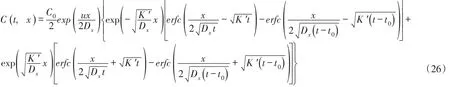
或

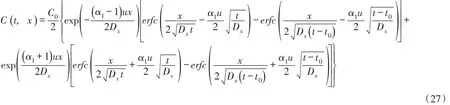
上游河段x＜0：

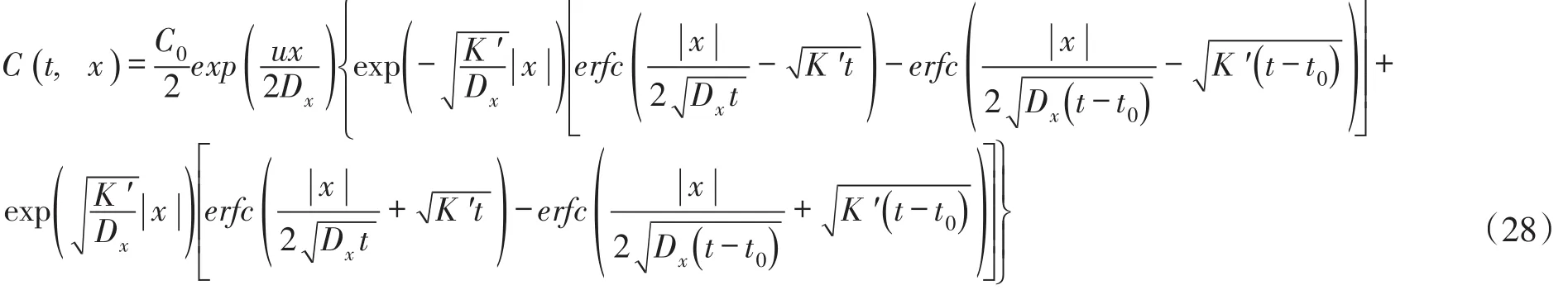
或

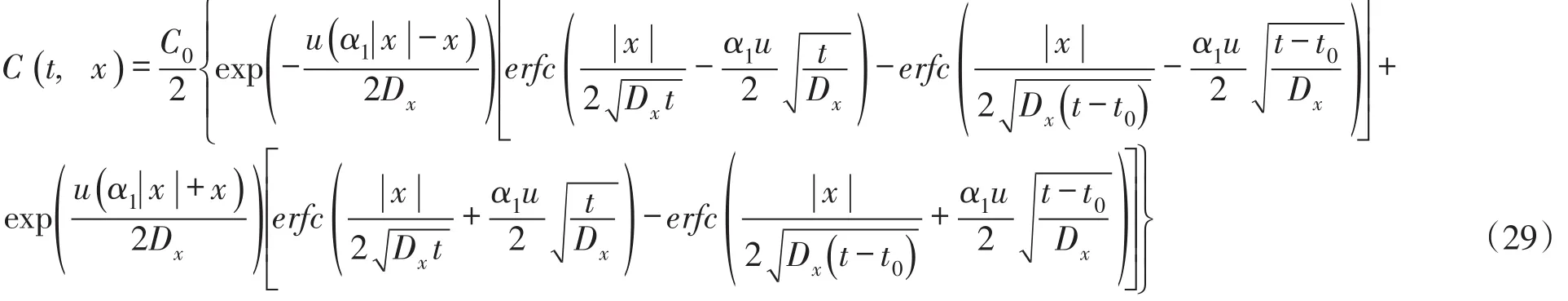
式（26）—（29）就是在有限时段源排放停止后t（t＞t0），排污口断面下游和上游河段一维水质模型方程污染物浓度分布的解析解。

根据污染源排放强度W（g/s）确定断面x=0处污染物初始稀释混合浓度C0的方法与文献［7］相同，计算公式为：

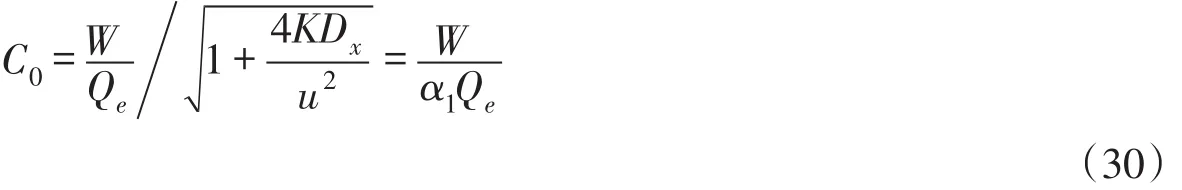
式中：Qe=Aeu为河流的环境设计流量［12］，Ae=BH为断面面积，B为平均河宽，H为平均水深。除排放强度和浓度外，其它变量和参数均采用m-s单位制。

注意到式（23）与式（25）以及式（27）与式（29）的结构形式对应相同，当x≥0时|x|=x，因此，可统一使用x＜0的式（25）或式（29）计算上、下游河段的污染物浓度分布。

3 有限时段源浓度分布分析与讨论

3.1浓度分布分析

①当u=0，0＜t≤t0时，式（22）变为：

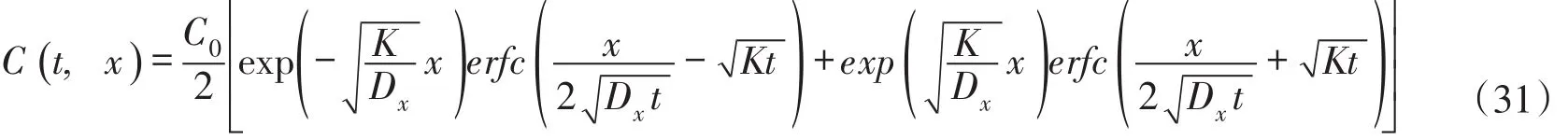
式（31）与文献［13］静止水体中连续源一维离散水质模型方程在x≥0时的解析解相同。连续源是指污染物的排放从时间t=0开始持续进行，在浓度计算时间污染物的排放没有结束。因此，在有限时段源排放持续期间（0＜t≤t0）的浓度分布公式，同样适用于连续源模型方程在相同求解条件下的浓度分布计算。

②当u=0，t→t0→∞时，式（22）和式（24）变为：

式（32）与文献［5］和教科书中一维稳态离散水质模型方程的解析解一致，有效浓度主要分布在的一段，在此范围内C/C0≥0.05。

③当K=0，0＜t≤t0时，式（22）变为：

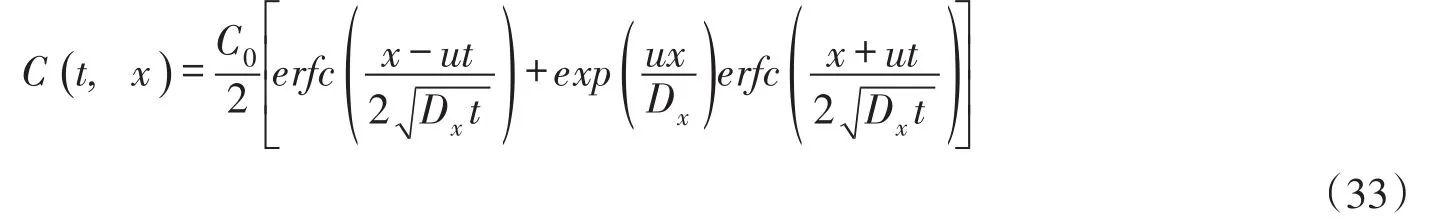
式（33）与文献［13-14］连续源一维移流离散水质模型方程在x≥0时的解析解相同。

④当u=0，K=0时，即有K ′=0，式（31）或式（26）变为：

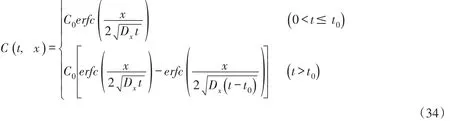
式（34）与文献［13］类似问题的解析解形式相同。

⑤当t→t0→∞时，有限时段源一维水质模型转化为恒定连续源的一维移流离散问题，又称为稳态源模型，式（23）和式（25）变为：

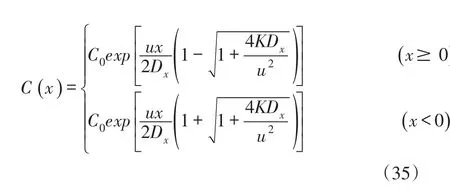
式（35）与文献［5］和教科书中一维稳态移流离散水质模型方程的解析解一致。

通过在特定条件下，对本文污染物浓度分布公式的简化与可对比解析解的一致性分析，表明经过严格数学推导以不同形式给出的污染物浓度分布解析式（22）—（29）的正确性。

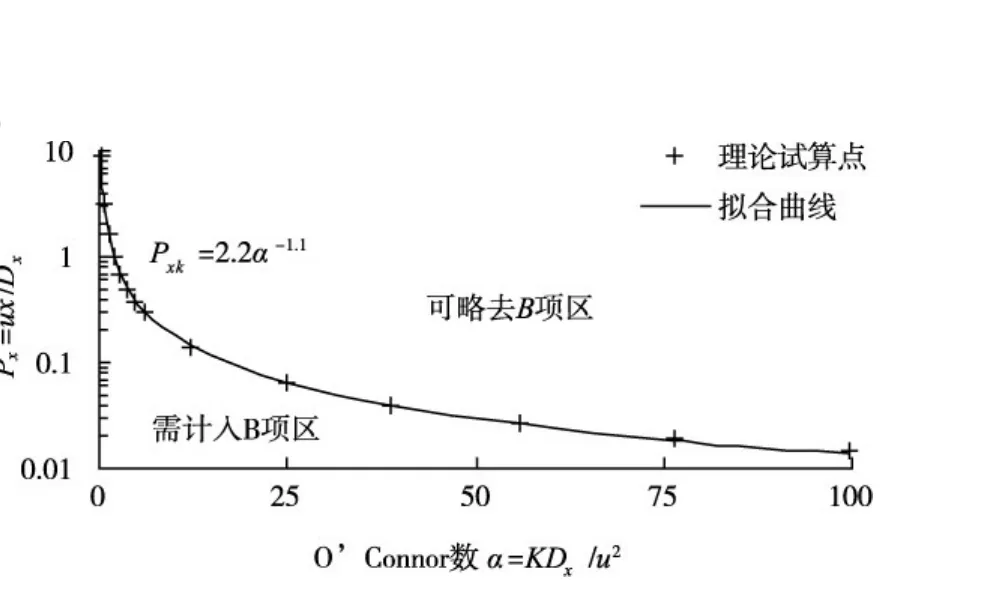
图1 在有限时段源浓度分布式（25）中是否计入B项的计算分区

3.2浓度分布讨论

①略去有限时段源浓度分布公式（25）中第二项的条件。在有限时段源排放持续期间（0＜t≤t0），对式（25）右边中括弧内［A+B］两项的贡献率作比较分析，以便对公式（25）进行简化处理。改写式（25）有：

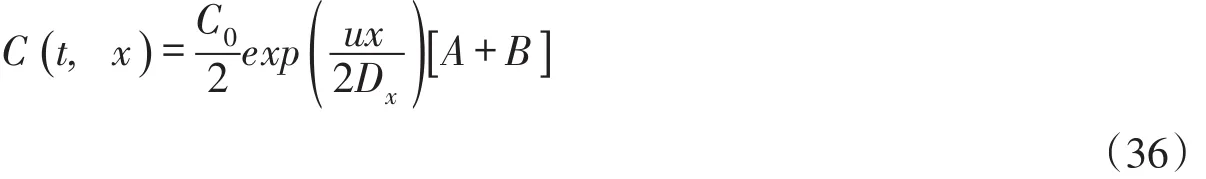
A、B均为偶函数，只讨论x≥0的情况。B/A的表达式为：

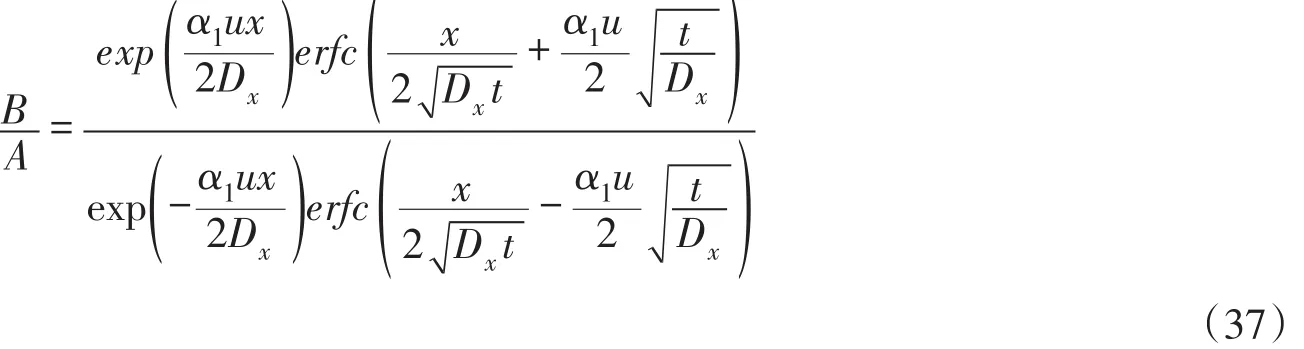
在文献［14］对式（33）右边中括弧内两项的贡献率作比较分析时得到：当ξ=ut/x=1时，出现函数式（33）的最大值；当ξ→∞时，出现函数式（33）的最小值→0。据此，假设t=x/u进行分析。设定在式（25）中可略去B项的计算条件为B/A≤0.05，并令注意到式（37）变为：

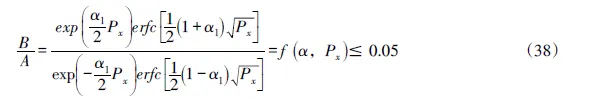
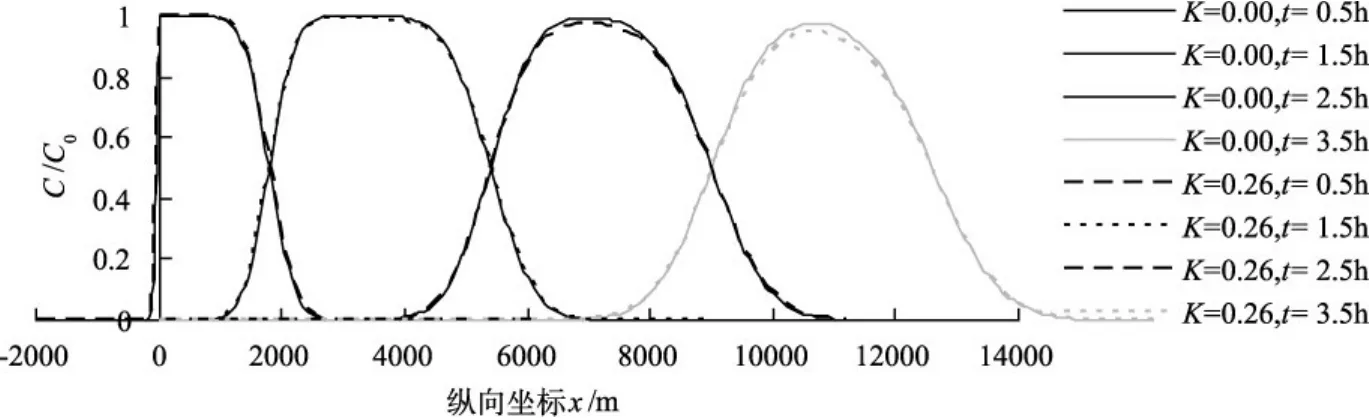
图2 有限时段源不同扩散历时的沿程浓度分布

依据式（38）的试算结果绘制无量纲Px（α）函数的半对数曲线，见图1。值得注意的是，在计算机标准函数库中，余误差函数erfc（z）只能取到z≥0时的值，当自变量z＜0时，使用余误差函数的性质erfc（-z）=2-erfc（z） 来计算。

由图1可知，在有限时段源浓度分布式（25）中可略去B项的计算条件为：

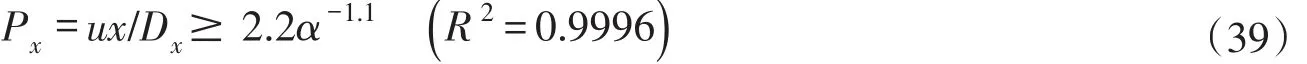
通常，在某计算河段的流速u和纵向离散系数Dx都为常数，当浓度计算点远离排污口时，式（39）很容易得到满足。即：除对小的|x|外，B项可以略去不计。同理可以推证，这一关系式仍然适用于对式（22）—（29）的简化处理。

②不考虑上游河段污染物浓度分布的条件。在有限时段源排放持续期间（0＜t≤t0），污染物向排污断面上、下游移流离散的影响范围不断扩大，污染影响长度逐步增长。当t→t0→∞时，排污断面上、下游的污染物浓度分布逐渐达到稳定状态，其污染影响长度达到最大。

文献［5-6］给出的河流稳态移流离散水质模型的简化分类条件，可作为有限时段源排放持续期间，污染物是否向上游（x＜0）离散迁移、是否考虑上游河段污染物浓度分布的判据，对环境管理是偏于安全的。该判别条件为：当O’Connor数和贝克来数时，移流作用占主导地位，天然河流的上中游河段大多属于此类情况，无需考虑排污断面上游的污染物浓

度分布；在其它条件下，均需对排污断面上游的污染物浓度分布进行计算。

当有限时段源排放停止后（t＞t0），对于α较大或者α较小且Wt≪ 1的情况，离散作用相对较大，污染物对排污断面上游的污染影响将会持续一段时间，逐渐消失；但对其余情况，污染物对排污断面上游的污染影响会迅速消失。

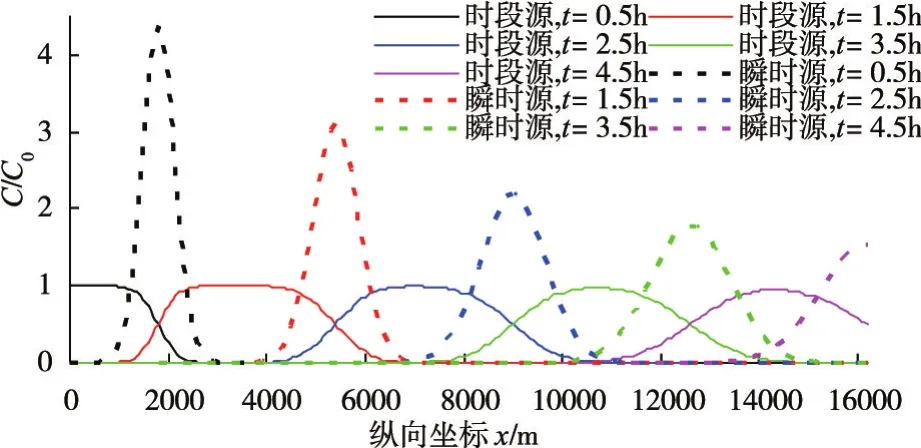
图3 时段源与瞬时源起始排放的沿程浓度分布比较

4 算例与对比分析

4.1有限时段源的算例分析设有限时段源的排放持续时间t0=1 h，排污断面x=0处的污染物初始稀释混合浓度C0保持不变，河流的平均流速u=1.0 m/s，纵向离散系数Dx=30 m2/s。则由式（25）和式（29）计算不同扩散历时t=0.5、1.5、2.5、3.5h的沿程污染物浓度分布，如图2所示。在图2中，实线表示降解速率系数K=0的保守物质，虚线表示降解速率系数K=0.26 d-1的非保守物质。

由图2看出，当0＜t≤t0时，有限时段源在x=0断面产生的污染物浓度维持不变，在移流作用下，浓度分布曲线出现了水平段；在离散作用下，出现浓度分布曲线向上游x＜0的急剧衰减下降段和向水平段下游的衰减下降曲线。当t=t0时有限时段源排放结束，之后出现浓度分布曲线向排污断面下游的整体移动，中间近似平顶段，浓度最大值对应的纵向坐标小于有限时段源排放中间点的迁移距离，即xc1＜xc=u（t-t0/2），两侧分别呈现向上、下游的衰减下降曲线。当扩散历时继续增大，浓度分布曲线的中间平顶段逐渐消失，浓度最大值对应的纵向坐标很快趋于有限时段源排放中间点的迁移距离，即xc1→xc，出现向下游比向上游的浓度下降过程稍缓的偏态分布。当t＞＞ t0、x较大时，浓度分布曲线趋于正态分布。图2还表明，由降解速率系数K引起的污染物衰减作用，使对应时间和空间点上的污染物浓度减小，当扩散历时越短，降解速率系数的作用越不明显，当扩散历时越长，高浓度减小的幅度稍大。

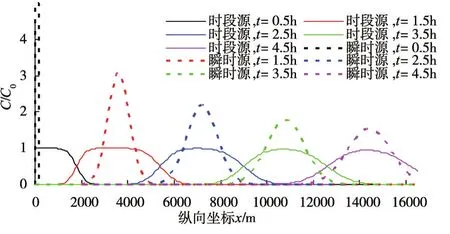
图4 时段源与瞬时源中间排放的沿程浓度分布比较

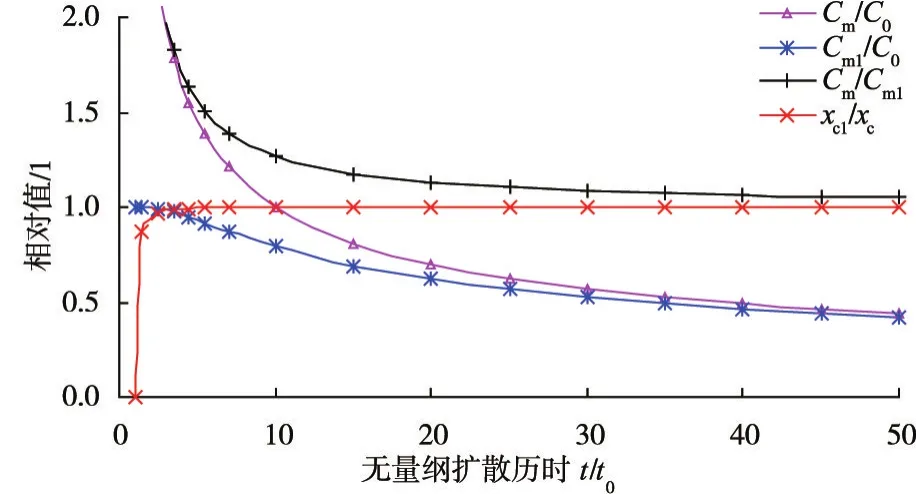
图5 时段源与瞬时源最大浓度和相应位置比较

4.2有限时段源与瞬时源浓度分布比较分析瞬时源一维移流离散水质模型方程式（1）的解析解为［2-3］：

式中：在x=0断面t=0时间突发瞬时源的污染物质量为M0，取其值等于有限时段源在排放持续期间的污染物总排放量Wt0，其它符号同前。

采用初始稀释混合浓度C0的表达式（30）对式（40）中的污染物浓度作无量纲处理，整理得到：

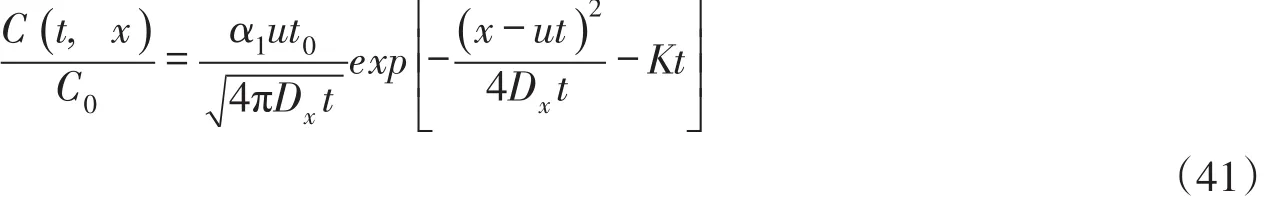
为便于比较，取河流特性和排污等计算参数与3.1节中相同，对降解速率系数K=0的保守物质进行分析。在瞬时源的突发时间t=0条件下，图3给出了不同扩散历时有限时段源与瞬时源沿程污染物浓度分布比较。

由图3看出，由于瞬时源是在x=0断面t=0时间突发出现，而有限时段源才刚刚开始排放，有限时段源在持续排放期间，瞬时源所产生的污染物沿程浓度分布，已逐渐离开起始排放断面出现在下游河段。由此看出，瞬时源产生的污染云质量中心（正态浓度分布的峰值点）与有限时段源产生的沿程浓度分布前沿同步，其污染云的质量中心提前有限时段源排放持续时间的一半t0/2到达下游河段同一位置。因此，在将有限时段源简化为瞬时源计算时，务必将瞬时源的突发时间移至有限时段源排放的中间时间t0/2进行计算。

将瞬时源的突发时间移至有限时段源排放的中间时间t0/2进行计算，式（41）变为：

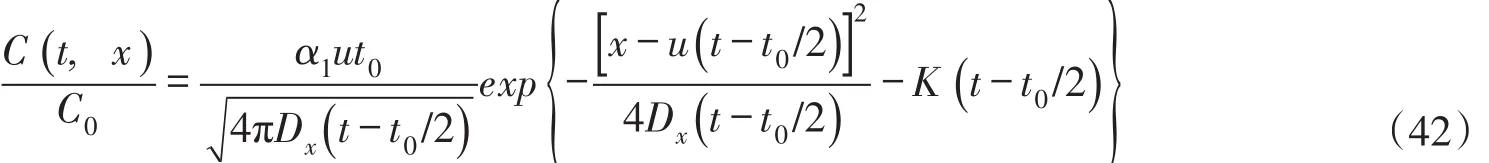
在瞬时源的突发时间t=t0/2条件下，图4给出了不同扩散历时有限时段源与瞬时源沿程污染物浓度分布比较；图5给出了瞬时源最大相对浓度（Cm/C0）、有限时段源最大相对浓度（Cm1/C0）和比值（Cm/Cm1）以及两者最大浓度相应位置的纵向坐标比值（xc1/xc）随时间的变化过程（下标“1”表示有限时段源的计算值，下同）。

由图4和图5看出，由于瞬时源是在x=0断面t=t0/2时间突发出现，因此，瞬时源产生的污染云质量中心与有限时段源产生的沿程浓度分布质量中心大致同步到达下游河段同一位置。但由于瞬时源是集中排放，污染云不容易离散开，当扩散历时较短，污染物最大浓度远超有限时段源。主要表现为瞬时源的沿程浓度分布曲线瘦高，污染物主要集中在最大值两侧附近，但瞬时源的污染物最大浓度沿程下降较快；而有限时段源的沿程浓度分布曲线扁平，浓度分布较宽，且污染物最大浓度沿程下降较缓慢，这种差别随着扩散历时的增长逐渐减小。对有限时段源与瞬时源的比较分析表明，在扩散历时t较短时，两者的沿程污染物浓度分布相差较大，有限时段源的最大浓度小于瞬时源，但时段源处于较高浓度的河段更长；在扩散历时t较长时，两者的沿程污染物浓度分布逐渐趋于一致。

由图5还看出，有限时段源与瞬时源最大浓度相应位置的纵向坐标比值（xc1/xc）很快趋于1，说明有限时段源沿程浓度分布曲线的中间平顶段消失后，浓度最大值对应的纵向坐标很快趋于有限时段源排放中间点的迁移距离，即xc1→xc=u（t-t0/2）。相比之下，瞬时源与有限时段源最大浓度比值（Cm/Cm1）趋于1的过程要缓慢得多，说明只有在扩散历时较长、两者预测的最大浓度接近时，才可以将有限时段源简化为按瞬时源计算。

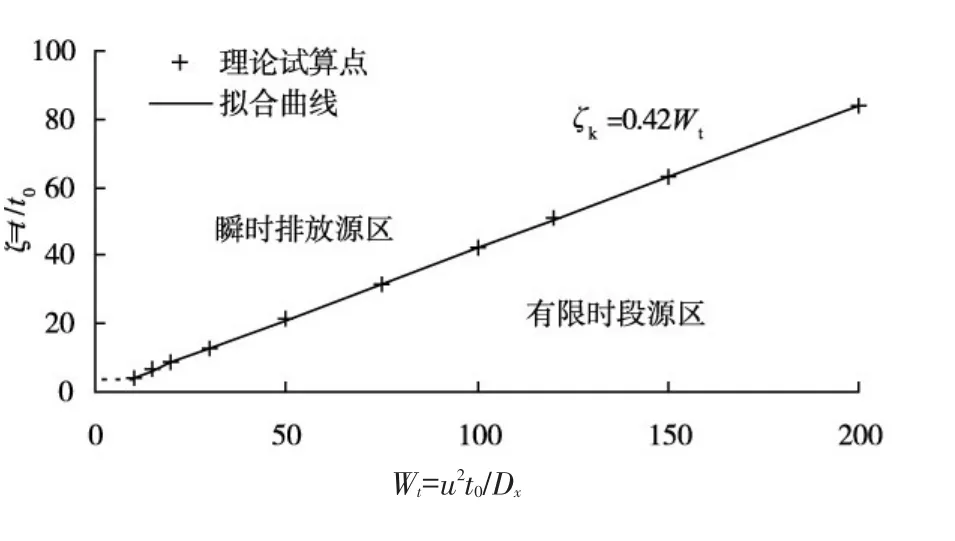
图6 有限时段源与瞬时源的计算分区

5 有限时段源按瞬时源计算的简化条件

5.1有限时段源与瞬时源计算临界点的定义在突发污染事故持续排放一段时间t0的情况下，若按瞬时源进行计算，在扩散历时较短时污染物的沿程浓度分布预测值偏离较大，但在扩散历时较长时两者的预测结果会逐渐接近。也就是说有限时段源与瞬时源的浓度最大值是一个渐近过程，据此定义：将按瞬时源与有限时段源进行计算的污染物最大浓度之比等于1.05的条件，作为可以简化为按瞬时源计算的临界时间tk确定依据。即：当扩散历时t≥tk时，污染物的沿程浓度分布可以按瞬时源的计算公式预测；否则，应按有限时段源的计算公式预测。下面讨论降解速率系数K=0保守物质的临界时间tk与排放持续时间t0及其相关因子的关系。

由式（42）可知，瞬时源的污染物最大浓度为：

由图4看出，由于有限时段源排放结束的时间滞后，污染物浓度分布中间出现近似平顶段，浓度最大值出现位置滞后，但当污染物浓度分布中间的平顶段很快消失时，有限时段源与瞬时源的浓度最大值出现位置很快趋于一致。即令x=xc=u（t-t0/2），代入式（26）整理得到有限时段源的污染物最大浓度为：

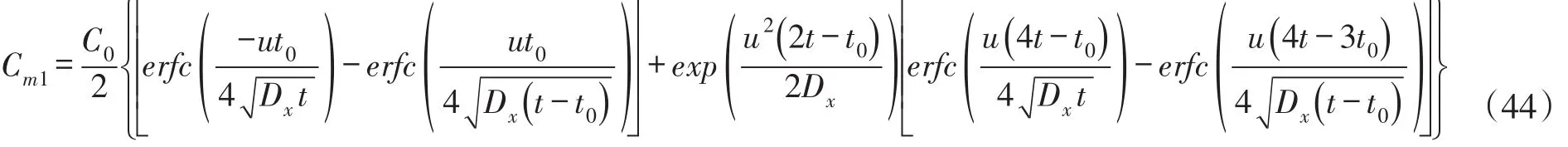
再令扩散历时t=ζt0，代入式（43）和式（44）分别得到瞬时源和有限时段源的污染物最大浓度为：

其中：无量纲数Wt=u2t0/Dx=us/Dx（称为排放数），表示有限时段源在持续排放期间的污染物迁移传递与离散传递通量之比；s=ut0为初始迁移长度。

5.2有限时段源简化为瞬时源的判据根据临界时间tk的定义，令式（45）与式（46）的比值等于1.05，则有：

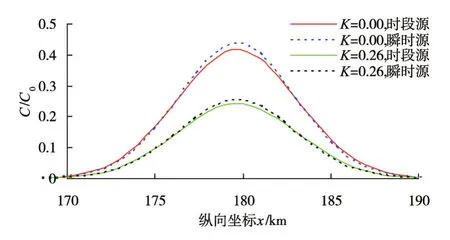
图7 在临界时间按时段源与瞬时源计算的沿程浓度分布比较

由式（47）的试算结果绘制无量纲临界时间ζk与无量纲数Wt的关系曲线，见图6。

当Wt＞10时，由图6中的理论试算点进行回归分析，得到有限时段源与瞬时源计算分区的无量

表1 在临界时间按时段源与瞬时源计算的沿程浓度分布特性比较

纲临界时间方程为：

由图6和式（48）可以看出，无量纲临界时间ζk与无量纲数Wt呈现良好的正比例关系。在河流平均流速和纵向离散系数不变的情况下，无量纲数Wt随排放持续时间t0的增加而增加，无量纲临界时间ζk同步增加。即排放持续时间越长，无量纲临界时间越大，有限时段源简化为按瞬时源计算需要的临界时间越长，相应的污染云质量中心纵向坐标xck=u（tk-t0/2）越远。

当Wt≤10时，由于同一扩散历时，有限时段源与瞬时源的浓度最大值不在同一位置出现，式（44）和式（46）均不能代表有限时段源的污染物最大浓度值，而且两者预测结果的沿程浓度分布特征差别较为明显，所以，此时的有限时段源不能简化为按瞬时源计算。在实际中，当无量纲数Wt较小，排放断面x=0附近区域处于污染物的初始稀释混合阶段，一维移流离散水质模型很难准确预测，再者扩散历时t较短，或小于应急反应时间，所以，可无需进行水质预测。分析认为，可将Wt=10时的无量纲临界时间ζk=4.20作为Wt≤10时的计算分区依据。

综上，有限时段源可以按瞬时源计算的简化条件，即从开始排放计算的扩散历时（时间）必须满足t≥tk=ζkt0，则有：

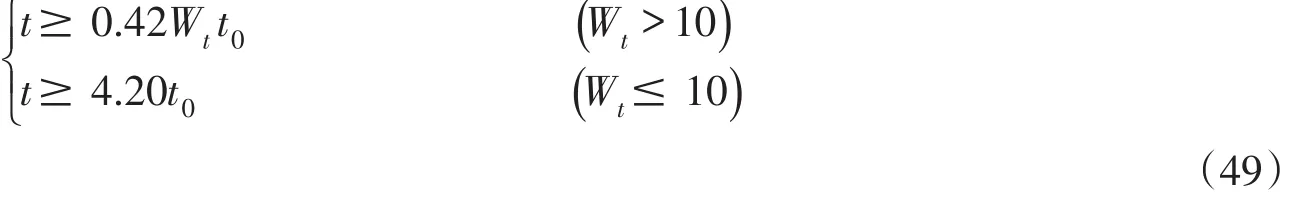
将Wt代入式（49）化简得到有限时段源简化为瞬时源的判别条件为：

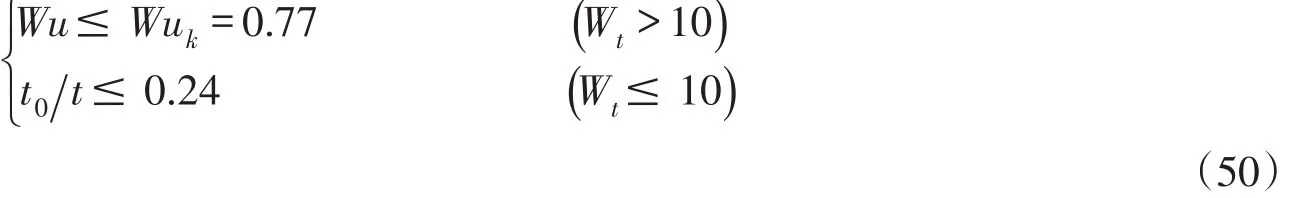
此时，相应的污染云质量中心纵向坐标xc=u（t-t0/2）≥（ζk-0.5）ut0，即：

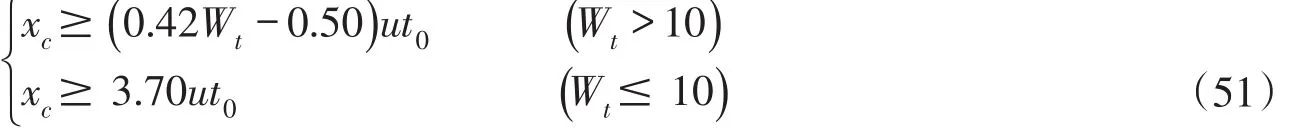
5.3分类临界状态的浓度分布比较及其标准差分析在3.2节中算例的给定参数条件下，计算得到无量纲数Wt=u2t0/Dx=120，由式（48）得到临界时间tk=50.40 t0=181440 s，相应的污染云质量中心纵向坐标xck=179.64 km。在降解速率系数K=0和K=0.26 d-1条件下，图7和表1给出了在临界时间按有限时段源和瞬时源计算的沿程浓度分布及特性比较。

由图7和表1可知，当降解速率系数K=0和K=0.26 d-1时，在临界时间的有限时段源按瞬时源计算，其最大浓度和浓度分布标准差的相对误差绝对值均小于等于5.0%。表明，在临界时间条件下，对降解速率系数K=0和K=0.26 d-1的情况，按瞬时源和有限时段源计算的沿程浓度分布曲线和特性均吻合良好。说明在降解速率系数K=0保守物质条件下，给出的有限时段源可以按瞬时源计算的临界时间tk（Wt）方程和简化判别条件，同样适用于K≠0的非保守物质。由图5可知，随着扩散历时的进一步增大，两者计算结果的相对误差将进一步减小，沿程浓度分布曲线和特性的吻合程度将进一步提高。

由此推论，在扩散历时t≥tk，即有限时段源可以按瞬时源计算的情况下，可以通过实测河段的沿程污染物浓度分布或河段纵向坐标x（≥xc）断面的污染物浓度过程线，按瞬时源的浓度分布公式反推，确定出该河段的纵向离散系数。

6 结论

（1）在等强度有限时段源条件下，给出了有限时段源排放持续期间和排放结束后，不同扩散历时河流沿程污染物浓度分布的解析解。分析表明，在不同简化条件下与可对比解析解完全一致。（2）给出了在有限时段源浓度分布公式中，可略去第二项的计算条件与无量纲分区曲线，以及可略去上游河段污染物浓度分布的判别条件。（3）定义了无量纲数Wt=u2t0/Dx，提出了有限时段源可以按瞬时源计算的临界时间tk（Wt）方程和简化判别条件：当扩散历时t＜tk，按有限时段源的浓度分布公式计算；当扩散历时t≥tk，且将污染事故的突发时间移至排放持续时段的中间时间t0/2，方可按瞬时源的浓度分布公式计算。（4）根据移流离散水质模型方程式（1）的线性特性，其解浓度分布符合叠加原理。因此，对变强度有限时段源可按时间坐标分成若干个排放时段单独计算，最后，按对应时间和空间进行浓度分布叠加计算。

［1］ HJ 169－2016，中华人民共和国国家环境保护标准·建设项目环境风险评价技术导则［S］.北京：中华人民共和国环境保护部，2016 .

［2］ 余常昭，马尔柯夫斯基M，李玉梁. 水环境中污染物扩散输移原理与水质模型［M］. 北京：中国环境科学出版社，1989：152-168 .

［3］ 张书农. 环境水力学［M］. 南京：河海大学出版社，1988：87-101 .

［4］ 吴燮荪. 河流水质数学模型及其解［J］. 污染防治技术，1995，8（1）：23-26 .

［5］ 武周虎. 河流移流离散水质模型的简化和分类判别条件分析［J］. 水利学报，2009，40（1）：27-32 .

［6］ 武周虎. 对移流离散水质模型分类参数Pe中特征长度的修正［J］. 青岛理工大学学报，2015，36（4）：7-9，41 .

［7］ 武周虎. 间隙性点源排放的一维移流离散［J］. 青岛大学学报：工程技术版，2000，15（1）：68-71 .

［8］ WU Zhouhu，Qiao Haitao . Advection and dispersion of substance discharged by intermittent point source in rivers［C］//Environmental Hydraulics and Sustainable Water Management，Vol.1. London：Taylor & Francis Group，2005：167-173 .

［9］ 彭应登，唐子华. 有限时段源模式在河流水质预测中的应用［J］. 环境保护，1990，18（2）：26-27 .

［10］ 武周虎. 基于环境扩散条件的河流宽度分类判别准则［J］. 水科学进展，2012，23（1）：53-58 .

［11］ 数学手册编写组. 数学手册［M］. 北京：高等教育出版社，1979：553-565 .

［12］ 武周虎，祝帅举，牟天瑜，等. 水环境影响预测中计算参数的确定及敏感性分析［J］. 人民长江，2016，47（8）：1-6 .

［13］ Wen-Hsiung Li . Differential equations of hydraulic transients，dispersion and groundwater flow . Mathematical Methods in Water Resources［M］. Prentice Hall，Inc，1972：184-195 .

［14］ Akio Ogata，R B Banks . A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media［R］.U. S. Geological Survey Professional Paper 411-A，U. S. Government Printing Office，Washington，D. C. 1961 .